174、【动态规划/贪心算法/滑动窗口】leetcode ——674. 最长连续递增序列:一题多解 (C++版本)
题目描述
解题思路
(1)双指针滑动窗口
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size();
if(n <= 1) return n;
int res = 1;
for(int i = 0; i < n; i++) {
int j = i;
while(j + 1 < n && nums[j] < nums[j + 1]) { // 寻找连续递增子序列
j++;
}
res = max(res, j + 1 - i); // 找到最长连续递增子序列
i = j;
}
return res;
}
};
(1)贪心算法
- 局部最优解:相邻子序列满足
nums[i - 1] < nums[i],满足的记录最新长度,不满足的更新新的起始下标重新记录。 - 全局最优解:整体的最长子序列
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size(), res = 1, start = 0;
for(int i = 1; i < n; i++) {
if(nums[i - 1] >= nums[i])
start = i;
res = max(res, i - start + 1);
}
return res;
}
};
(2)动态规划
- 动态规划五步曲:
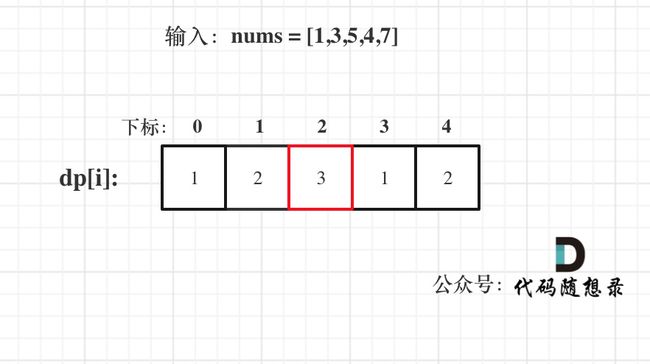
(1)dp[i]含义: 从下标i往前的最长连续子序列长度。
(2)递推公式: dp[i] = dp[i - 1] + 1,每遇到一个连续的字符,就在上一个已有的最长子序列长度上加一。
(3)dp数组初始化: dp[i] = 1,自身最少为一个。
(4)遍历顺序: 从左到有。
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size(), res = 1;
vector<int> dp(n + 1, 1);
for(int i = 1; i < n; i++) {
if(nums[i - 1] < nums[i]) {
dp[i] = dp[i - 1] + 1;
}
res = max(res, dp[i]);
}
return res;
}
};
参考文章:674. 最长连续递增序列