NLP--Transformer探索(微观)【笔记】
系列文章
LLM模型成为市场上的热宠,BERT、GPT系列让人们趋之若鹜,尤其对于2023年来说,ChatGPT出来后,市面上呈现出“洛阳纸贵”“万人空巷”之势。对于模型的演变历程中,Transformer——“You should go to the learning”,因为其出现才是开天辟地的大作。
- NLP–Transformer探索(宏观)【笔记】
- NLP–Transformer探索(微观)【笔记】
前言
此篇为对Transformer学习记录的第二篇。
上一篇我们从宏观上对Transformer的输入进行了了解,此文是从微观上对Transformer的细节进行学习。Let’s go!
seq2seq
seq2seq(sequence to sequence):序列到序列
seq2seq模型
(1)输入可以是一个(单词、字母或者图像特征)序列,
(2)输出是另外一个(单词、字母或者图像特征)序列
seq2seq模型由编码器(Encoder)和解码器(Decoder)组成
seq2seq工作流程:
编码器会处理输入序列中的信息转换成Context向量,然后解码器将Context向量信息转换成新序列。(编码器首先按照时间步依次编码每个单词,最终将最后一个hidden state也就是context向量传递给解码器,解码器根据context向量逐步解码得到文本输出。)
Context向量是数组,是基于编码器RNN的隐藏神经元数量(编码器逐步得到hidden state并传输最后一个hidden state给解码器)
Attention
RNN的seq2seq中Context向量缺点:
- 单个向量很难包含所有文本序列的信息(信息不全)
- RNN递归地编码文本序列使得模型在处理长文本时面临非常大的挑战(遗忘问题)
attention注意力机制,使得seq2seq模型可以有区分度、有重点地关注输入序列
attention可以简单理解为:一种有效的加权求和技术,其艺术在于如何获得权重。
一个注意力模型与经典的seq2seq模型主要有2点不同:
- 编码器会把更多的数据传递给解码器。编码器把所有时间步的 hidden state(隐藏层状态) 传递给解码器,而不是只传递最后一个 hidden state(隐藏层状态)
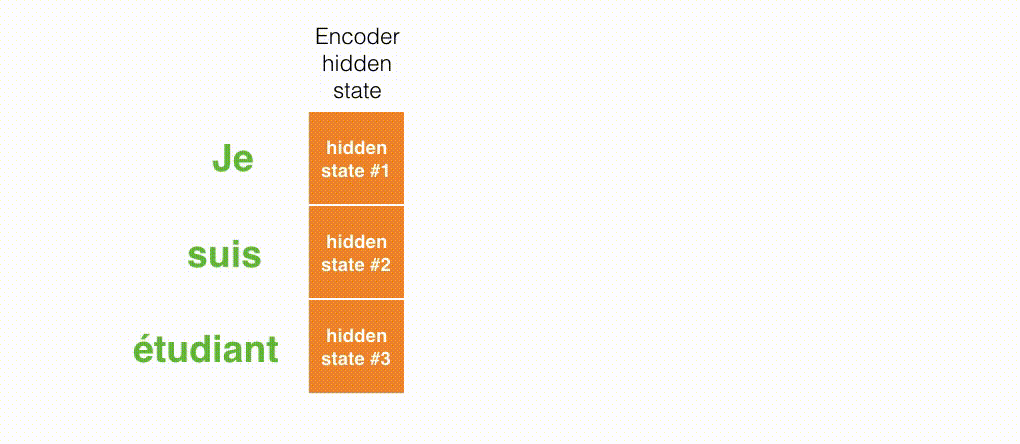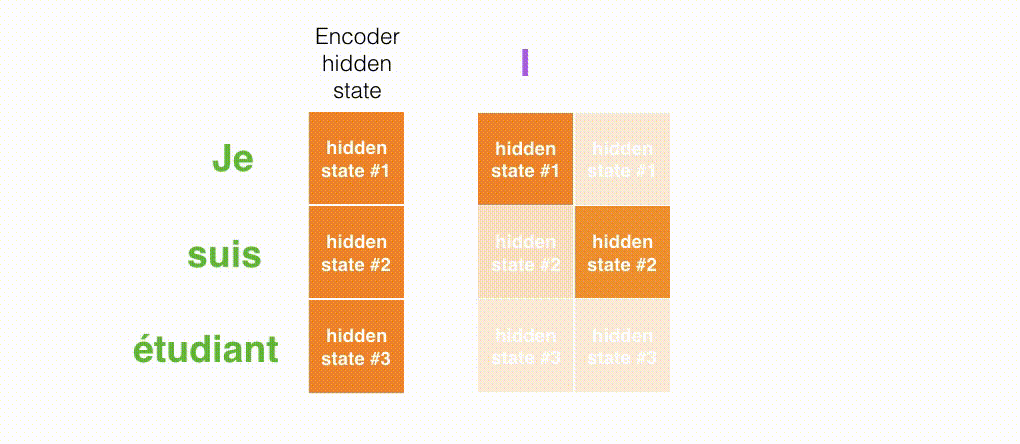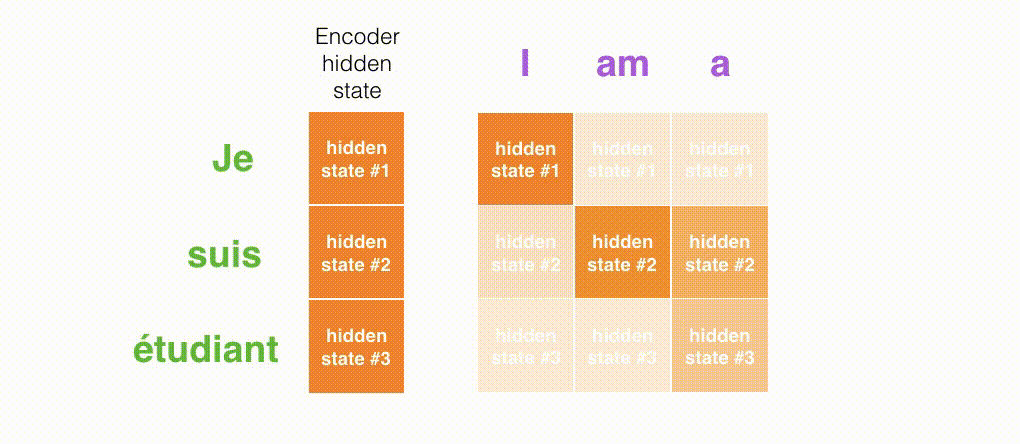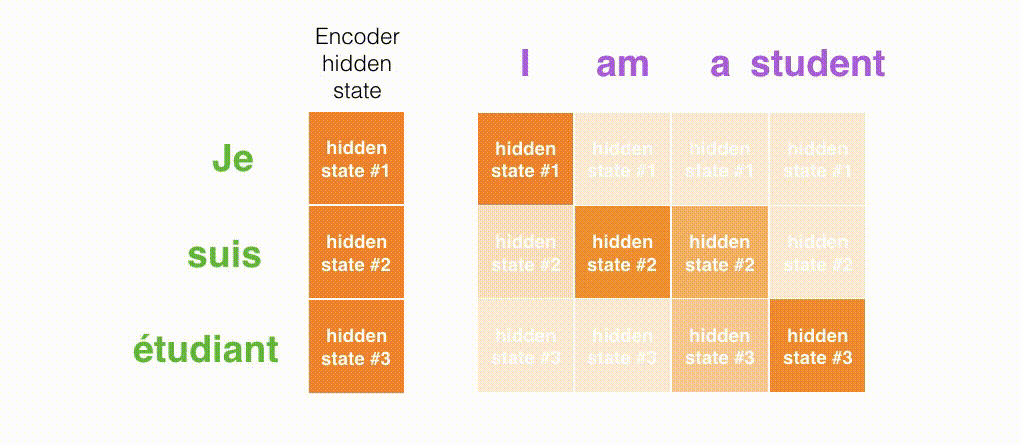
- 注意力模型的解码器在产生输出之前,做了一个额外的attention处理。如下图所示,具体为:
- 由于编码器中每个 hidden state(隐藏层状态)都对应到输入句子中一个单词,那么解码器要查看所有接收到的编码器的 hidden state。
- 给每个 hidden state计算出一个分数(我们先忽略这个分数的计算过程)。
- 所有hidden state的分数经过softmax进行归一化。
- 将每个 hidden state乘以所对应的分数,从而能够让高分对应的 hidden state会被放大,而低分对应的 hidden state会被缩小。
- 将所有hidden state根据对应分数进行加权求和,得到对应时间步的context向量。
结合注意力的seq2seq模型解码器全流程,动态图展示的是第4个时间步:
- 注意力模型的解码器 RNN 的输入包括:一个word embedding 向量,和一个初始化好的解码器 hidden state,图中是 h i n i t h_{init} hinit。
- RNN 处理上述的 2 个输入,产生一个输出和一个新的 hidden state,图中为h4。
- 注意力的步骤:我们使用编码器的所有 hidden state向量和 h4 向量来计算这个时间步的context向量(C4)。
- 我们把 h4 和 C4 拼接起来,得到一个橙色向量。
- 我们把这个橙色向量输入一个前馈神经网络(这个网络是和整个模型一起训练的)。
- 根据前馈神经网络的输出向量得到输出单词:假设输出序列可能的单词有N个,那么这个前馈神经网络的输出向量通常是N维的,每个维度的下标对应一个输出单词,每个维度的数值对应的是该单词的输出概率。
- 在下一个时间步重复1-6步骤。
注意力模型不是无意识地把输出的第一个单词对应到输入的第一个单词,它是在训练阶段学习到如何对两种语言的单词进行对应
Transformer
与RNN神经网络相比,Transformer的优点:
模型在处理序列输入时,可以对整个序列输入进行并行计算,不需要按照时间步循环递归处理输入序列。
Transformer模型结构中的左半部分为编码器(encoder),右半部分为解码器(decoder)
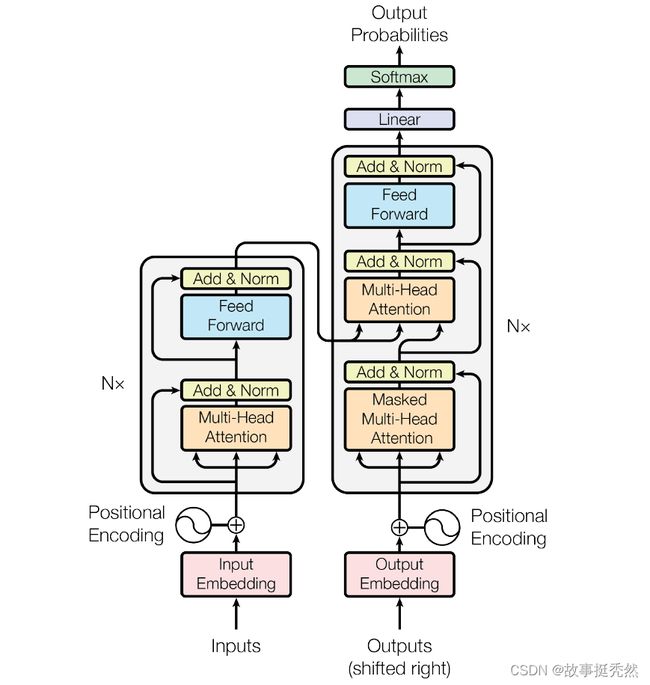
Transformer编码层和解码层有多层,每层编解码层网络结构一样。
不同编码层和解码层网络结构不共享参数。
Encoder框架
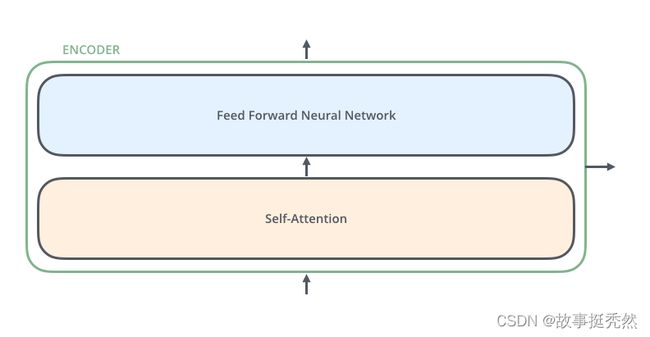
单层Encoder组成
- Self-Attention Layer
- Feed Forward Neural Network(前馈神经网络,缩写为FFNN)
Encoder流程
文本序列 ⟹ \Longrightarrow ⟹ 向量序列(Word-Embedding + + + Positional-Encoding) ⟹ \Longrightarrow ⟹ Self-Attention Layer(向量) ⟹ \Longrightarrow ⟹ FFNN(向量) ⟹ \Longrightarrow ⟹ Self-Attention Layer ⟹ \Longrightarrow ⟹ … n层 … ⟹ \Longrightarrow ⟹ FFNN(向量) ⟹ \Longrightarrow ⟹。。。
Encoder(编码器) 步骤
- 编码器的输入文本序列 w 1 , w 2 , . . . , w n w_1, w_2,...,w_n w1,w2,...,wn最开始需要经过embedding转换,得到每个单词的向量表示 x 1 , x 2 , . . . , x n x_1, x_2,...,x_n x1,x2,...,xn,其中 x i ∈ R d x_i \in \mathbb{R}^{d} xi∈Rd是维度为 d d d的向量。(Embedding)
- 然后所有向量经过一个Self-Attention神经网络层进行变换和信息交互得到 h 1 , h 2 , . . . h n h_1, h_2,...h_n h1,h2,...hn,其中 h i ∈ R d h_i \in \mathbb{R}^{d} hi∈Rd是维度为 d d d的向量。self-attention层处理一个词向量的时候,不仅会使用这个词本身的信息,也会使用句子中其他词的信息(你可以类比为:当我们翻译一个词的时候,不仅会只关注当前的词,也会关注这个词的上下文的其他词的信息)。(Self-Attention)
- Self-Attention层的输出会经过前馈神经网络得到新的 x 1 , x 2 , . . , x n x_1, x_2,..,x_n x1,x2,..,xn,依旧是 n n n个维度为 d d d的向量。(FFNN)
- 这些向量将被送入下一层encoder,继续相同的操作。(循环上述 2,3)
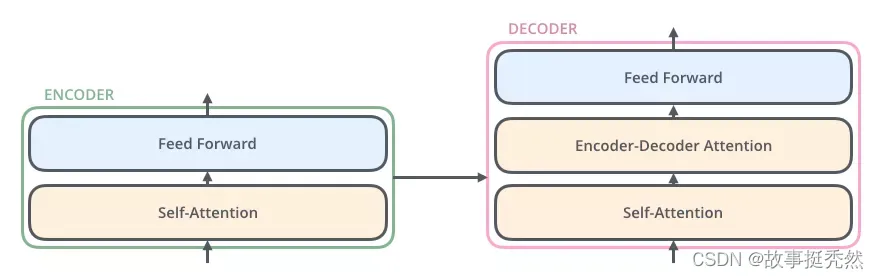
Decoder框架
解码器在编码器的self-attention和FFNN中间插入了一个Encoder-Decoder Attention层,这个层帮助解码器聚焦于输入序列最相关的部分
输入处理
-
词向量(词嵌入 Word-Embedding):将输入文本序列的每个词转换为一个词向量。
在实际应用中,我们通常会同时给模型输入多个句子,如果每个句子的长度不一样,我们会选择一个合适的长度,作为输入文本序列的最大长度:如果一个句子达不到这个长度,那么就填充先填充一个特殊的**“padding”词;如果句子超出这个长度,则做截断**。
最大序列长度是一个超参数,通常希望越大越好,但是更长的序列往往会占用更大的训练显存/内存,因此需要在模型训练时候视情况进行决定。 -
位置向量:对每个输入的词向量都加上了一个位置向量。
这些向量有助于确定每个单词的位置特征,或者句子中不同单词之间的距离特征。
输入序列的向量表示 = = = 词向量 + + + 位置向量
(两者相加可为模型提供更多有意义的信息,比如词的位置,词之间的距离等)
位置编码信息向量计算
-
原始论文中给出的设计表达式为: P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d model ) , P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d model ) PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{\text{model}}}) ,PE_{(pos,2i+1)} = cos(pos / 10000^{2i/d_{\text{model}}}) PE(pos,2i)=sin(pos/100002i/dmodel),PE(pos,2i+1)=cos(pos/100002i/dmodel) 上面表达式中的 p o s pos pos代表词的位置, d m o d e l d_{model} dmodel代表位置向量的维度, i ∈ [ 0 , d m o d e l ) i \in [0, d_{model}) i∈[0,dmodel)代表位置 d m o d e l d_{model} dmodel维位置向量第 i i i维。于是根据上述公式,我们可以得到第 p o s pos pos位置的 d m o d e l d_{model} dmodel维位置向量。
-
位置编码信息计算方式优点:
- 可以扩展到未知的序列长度。
例如:当我们的模型需要翻译一个句子,而这个句子的长度大于训练集中所有句子的长度,这时,这种位置编码的方法也可以生成一样长的位置编码向量。
- 可以扩展到未知的序列长度。
Self-Attention
The animal didn't cross the street because it was too tired
如果模型引入了Self Attention机制之后,便能够让模型把it和animal关联起来了。同样的,当模型处理句子中其他词时,Self Attention机制也可以使得模型不仅仅关注当前位置的词,还会关注句子中其他位置的相关的词,进而可以更好地理解当前位置的词。
RNN 在处理序列中的一个词时,会考虑句子前面的词传过来的hidden state,而hidden state就包含了前面的词的信息;而Self Attention机制值得是,当前词会直接关注到自己句子中前后相关的所有词语
什么是“self-attention自注意力机制”?
假设一句话包含两个单词:Thinking Machines。
自注意力的一种理解是:Thinking-Thinking,Thinking-Machines,Machines-Thinking,Machines-Machines,共 2 2 2^2 22种两两attention。
如何计算 self-attention?(步骤)
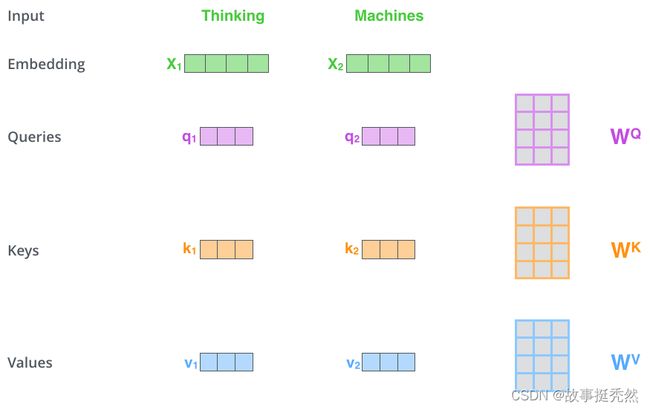
假设Thinking、Machines这两个单词经过词向量算法得到向量是 X 1 , X 2 X_1, X_2 X1,X2:
- q 1 = X 1 W Q , q 2 = X 2 W Q q_1 = X_1 W^Q, q_2 = X_2 W^Q q1=X1WQ,q2=X2WQ;
$ k_1 = X_1 W^K, k_2 = X_2 W^K$;
v 1 = X 1 W V , v 2 = X 2 W V v_1 = X_1 W^V, v_2 = X_2 W^V v1=X1WV,v2=X2WV,
$W^Q, W^K, W^K \in \mathbb{R}^{d_x \times d_k}\ $ - $score_{11} = \frac{q_1 \cdot q_1}{\sqrt{d_k}},score_{12} = \frac{q_1 \cdot q_2}{\sqrt{d_k}} $;
- s c o r e 21 = q 2 ⋅ q 1 d k , s c o r e 22 = q 2 ⋅ q 2 d k score_{21} = \frac{q_2 \cdot q_1}{\sqrt{d_k}},score_{22} = \frac{q_2 \cdot q_2}{\sqrt{d_k}} score21=dkq2⋅q1,score22=dkq2⋅q2;
- s c o r e 11 = e s c o r e 11 e s c o r e 11 + e s c o r e 12 , s c o r e 12 = e s c o r e 12 e s c o r e 11 + e s c o r e 12 score_{11} = \frac{e^{score_{11}}}{e^{score_{11}} + e^{score_{12}}},score_{12} = \frac{e^{score_{12}}}{e^{score_{11}} + e^{score_{12}}} score11=escore11+escore12escore11,score12=escore11+escore12escore12;
s c o r e 21 = e s c o r e 21 e s c o r e 21 + e s c o r e 22 , s c o r e 22 = e s c o r e 22 e s c o r e 21 + e s c o r e 22 score_{21} = \frac{e^{score_{21}}}{e^{score_{21}} + e^{score_{22}}},score_{22} = \frac{e^{score_{22}}}{e^{score_{21}} + e^{score_{22}}} score21=escore21+escore22escore21,score22=escore21+escore22escore22 - z 1 = v 1 × s c o r e 11 + v 2 × s c o r e 12 z_1 = v_1 \times score_{11} + v_2 \times score_{12} z1=v1×score11+v2×score12;
$z_2 = v_1 \times score_{21} + v_2 \times score_{22} $
self-attention计算步骤
第一步:
将词向量(WE + Position)进行线性变换得到:
- Query向量: q 1 , q 2 q_1,q_2 q1,q2
- Key向量: k 1 , k 2 k_1,k_2 k1,k2
- Value向量: v 1 , v 2 v_1,v_2 v1,v2。
这3个向量是词向量分别和3个参数矩阵( W W W)相乘得到的,而这个矩阵也是是模型要学习的参数。(Query、Key、Value只是3个被冠上特殊名称的向量,为了更好理解Self-Attention)
Attention计算逻辑:query和key计算相关或者叫attention得分,然后根据attention得分对value进行加权求和。
第二步:
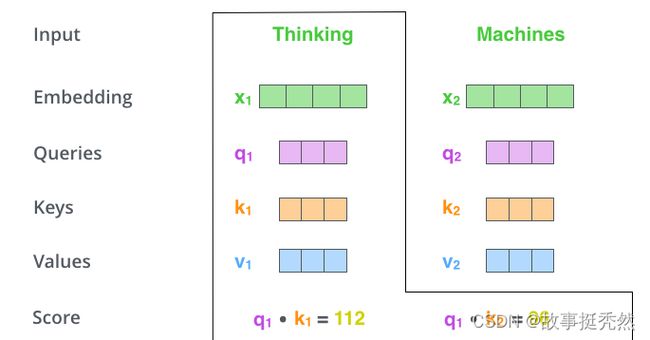
计算Attention Score(注意力分数)
假设我们现在计算第一个词Thinking 的Attention Score(注意力分数),需要根据Thinking 对应的词向量,对句子中的其他词向量都计算一个分数。这些分数决定了我们在编码Thinking这个词时,需要对句子中其他位置的词向量的权重。
Attention score是根据"Thinking" 对应的 Query 向量和其他位置的每个词的 Key 向量进行点积得到的。Thinking的第一个Attention Score就是 q 1 q_1 q1和 k 1 k_1 k1的内积,第二个分数就是 q 1 q_1 q1和 k 2 k_2 k2的点积。这个计算过程在下图中进行了展示,下图里的具体得分数据是为了表达方便而自定义的。
第三步:
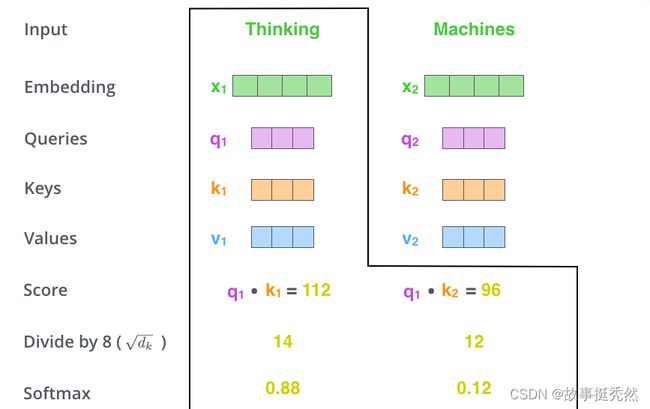
把每个分数除以 d k \sqrt{d_k} dk, d k d_{k} dk是Key向量的维度。
( d k \sqrt{d_k} dk是为了在反向传播时,求梯度更加稳定)
第四步:
分数经过一个Softmax函数,Softmax可以将分数归一化,这样使得分数都是正数并且加起来,和为1
第五步:
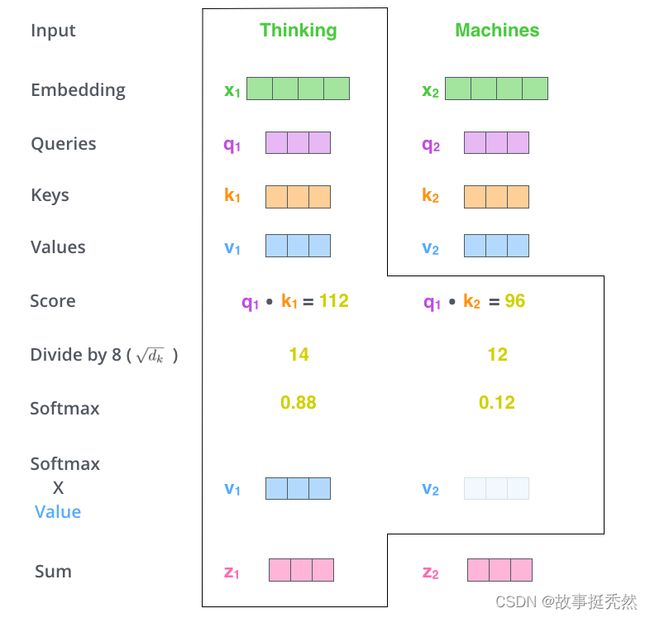
得到每个词向量的分数后,将分数分别与对应的Value向量相乘
(对于分数高的位置,相乘后的值就越大,我们把更多的注意力放到了它们身上;对于分数低的位置,相乘后的值就越小,这些位置的词可能是相关性不大的)
第六步:
把第5步得到的Value向量相加,就得到了Self Attention在当前位置(这里的例子是第1个位置)对应的输出。(加权求和)
上面的6个步骤每次只能计算一个位置的输出向量,在实际的代码实现中,Self Attention的计算过程是使用矩阵快速计算的,一次就得到所有位置的输出向量。
将self-attention计算6个步骤中的向量放一起,比如 X = [ x 1 ; x 2 ] X=[x_1;x_2] X=[x1;x2],便可以进行矩阵计算啦。下面,依旧按步骤展示self-attention的矩阵计算方法。 X = [ X 1 ; X 2 ] , Q = X W Q , K = X W K , V = X W V , Z = s o f t m a x ( Q K T d k ) V X = [X_1;X_2] ,\ Q = X W^Q, K = X W^K, V=X W^V ,\ Z = softmax(\frac{QK^T}{\sqrt{d_k}}) V X=[X1;X2], Q=XWQ,K=XWK,V=XWV, Z=softmax(dkQKT)V
self-attention矩阵计算方法
第1步:
计算 Query,Key,Value 的矩阵。首先,我们把所有词向量放到一个矩阵X中,然后分别和3个权重矩阵 W Q , W K W V W^Q, W^K W^V WQ,WKWV 相乘,得到 Q,K,V 矩阵。矩阵X中的每一行,表示句子中的每一个词的词向量。Q,K,V 矩阵中的每一行表示 Query向量,Key向量,Value 向量,向量维度是 d k d_k dk。
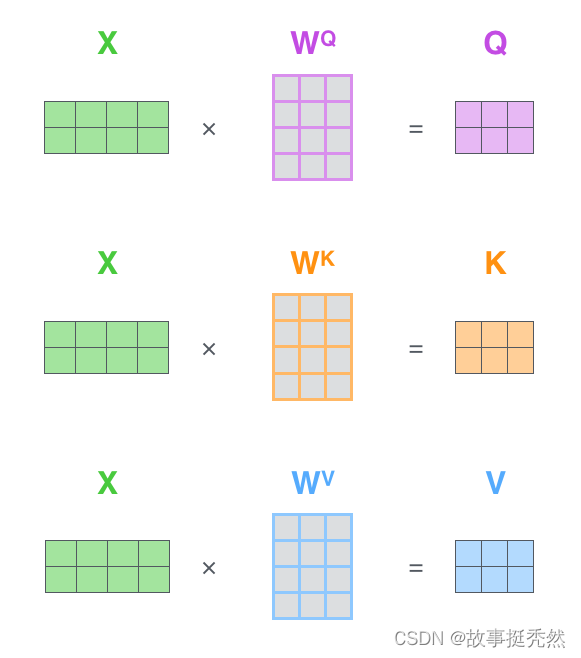
第2步:
由于我们使用了矩阵来计算,我们可以把上面self-attention计算步骤的第 2 步到第 6 步压缩为一步,直接得到 Self Attention 的输出。
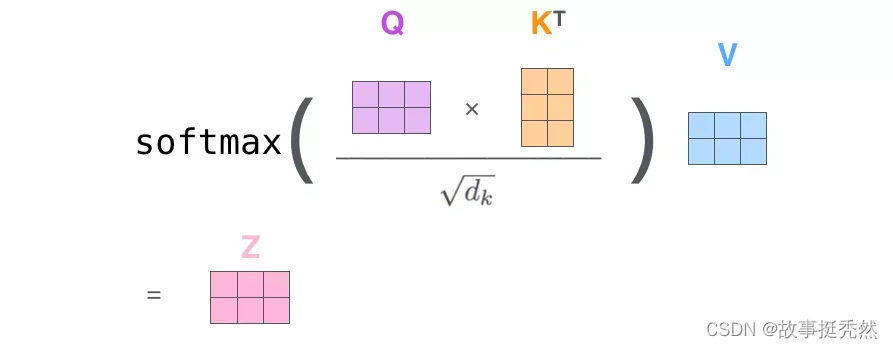
Multi-head
多头注意力机制增强Attention层的能力:
- 它扩展了模型关注不同位置的能力。在上面的例子中,第一个位置的输出 z 1 z_1 z1包含了句子中其他每个位置的很小一部分信息,但 z 1 z_1 z1仅仅是单个向量,所以可能仅由第1个位置的信息主导了。而当我们翻译句子:
The animal didn’t cross the street because it was too tired时,我们不仅希望模型关注到"it"本身,还希望模型关注到"The"和“animal”,甚至关注到"tired"。这时,多头注意力机制会有帮助。 - 多头注意力机制赋予attention层多个“子表示空间”。下面我们会看到,多头注意力机制会有多组 W Q , W K , W V W^Q, W^K, W^V WQ,WK,WV 的权重矩阵(在 Transformer 的论文中,使用了 8 组注意力),,因此可以将 X X X变换到更多种子空间进行表示。接下来我们也使用8组注意力头(attention heads))。每一组注意力的权重矩阵都是随机初始化的,但经过训练之后,每一组注意力的权重 W Q , W K W V W^Q, W^K W^V WQ,WKWV 可以把输入的向量映射到一个对应的”子表示空间“。
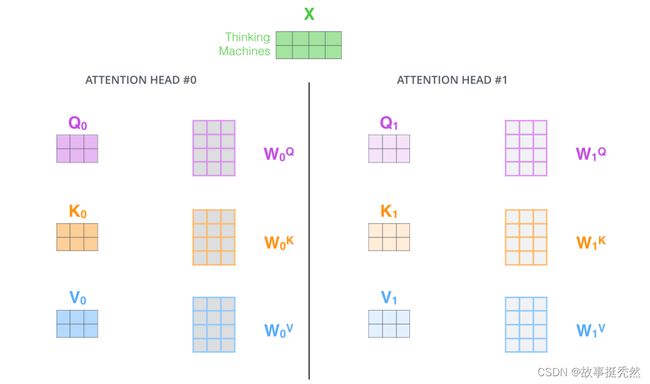
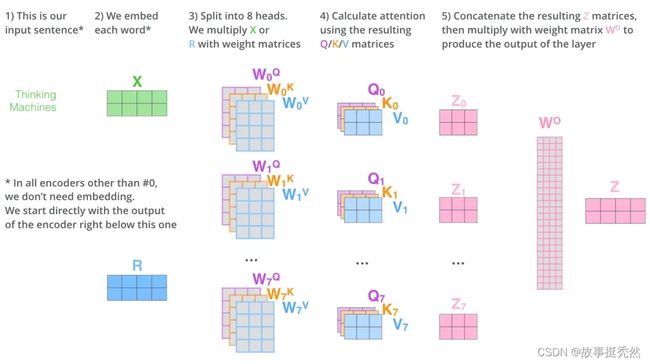
第一步:
在多头注意力机制中,我们为每组注意力设定单独的 WQ, WK, WV 参数矩阵。将输入X和每组注意力的WQ, WK, WV 相乘,得到8组 Q, K, V 矩阵。
接着,我们把每组 K, Q, V 计算得到每组的Z 矩阵,就得到8个Z矩阵。
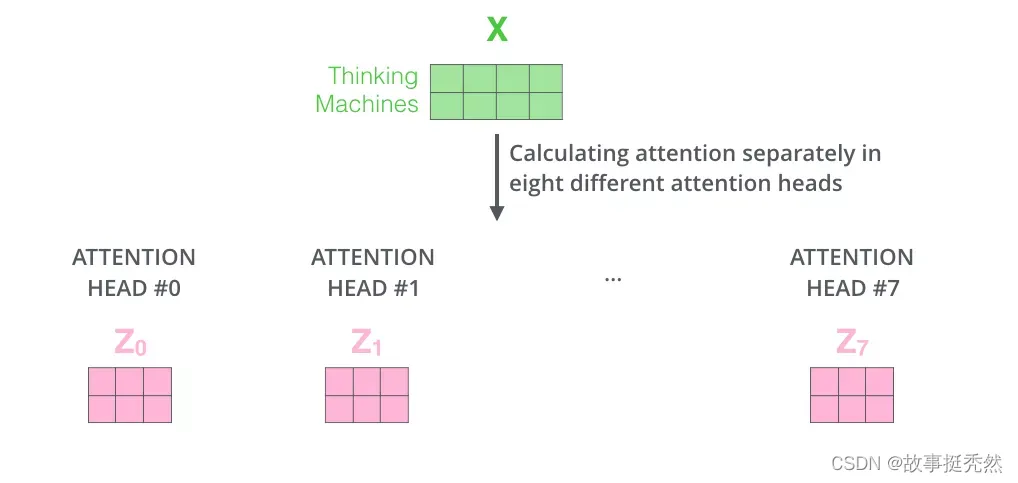
第二步:
由于前馈神经网络层接收的是 1 个矩阵(其中每行的向量表示一个词),而不是 8 个矩阵,所以我们直接把8个子矩阵拼接起来得到一个大的矩阵。
第三步:
然后和另一个权重矩阵 W O W^O WO相乘做一次变换,映射到前馈神经网络层所需要的维度。
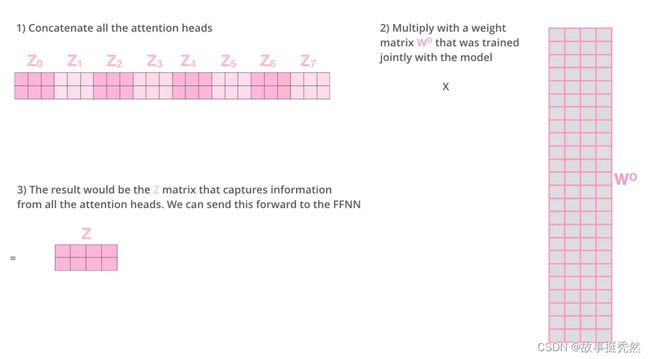
多头注意力(multi-head):
- 将多头矩阵(Q、K、V)映射到一个Z矩阵,将多个Z矩阵拼接起来为一个矩阵
- 将这一个拼接矩阵和权重 W O W^O WO相乘
- 最终得到一个矩阵Z,包含所有attention heads(注意力头)的信息,将这个矩阵输入的FFNN(Feed Forward Neural Network)
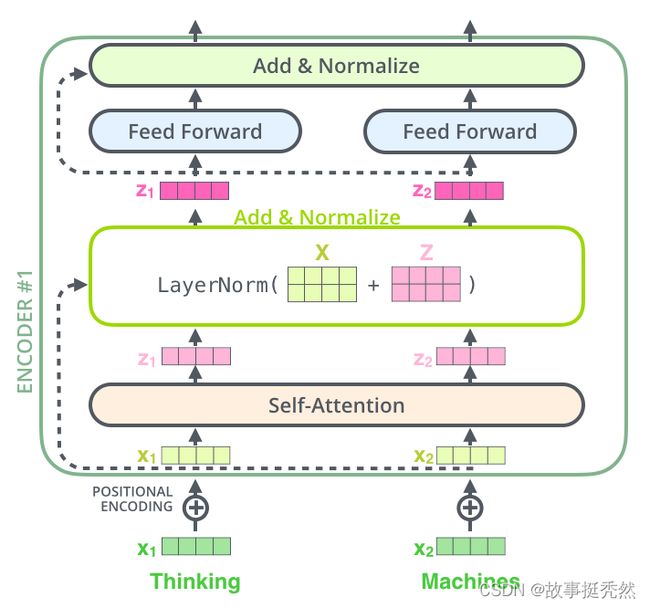
残差链接和标准化
编码器的每个子层(Self Attention 层和 FFNN)都有一个残差连接和层标准化(layer-normalization)
输出处理
解码器中的 Self Attention 层,和编码器中的 Self Attention 层的区别:
- 在解码器里,Self Attention 层只允许关注到输出序列中早于当前位置之前的单词。具体做法是:在 Self Attention 分数经过 Softmax 层之前,屏蔽当前位置之后的那些位置(将attention score设置成-inf)。
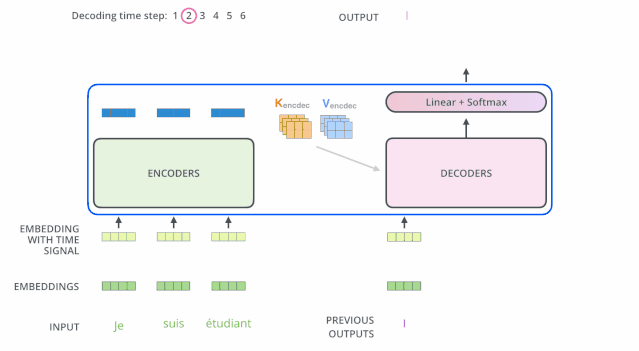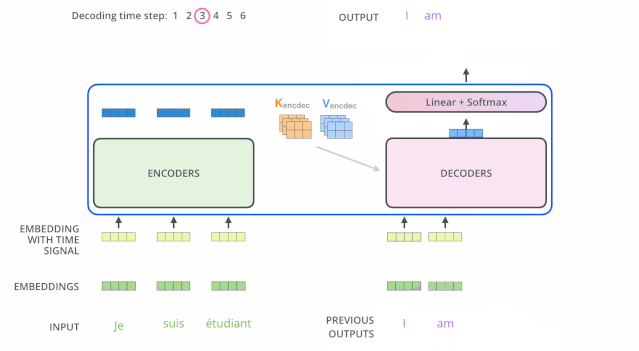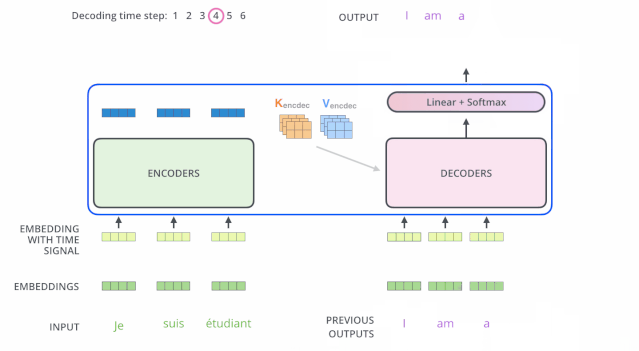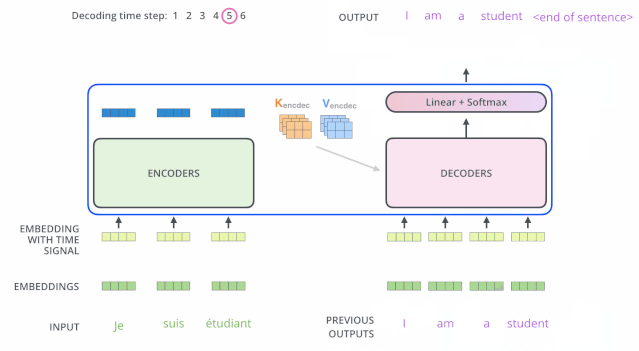
- 解码器 Attention层是使用前一层的输出来构造Query 矩阵,而Key矩阵和 Value矩阵来自于编码器最终的输出。
线性层和softmax
Decoder 最终的输出是一个向量,其中每个元素是浮点数
将向量转换为单词的步骤:
- 线性层就是一个普通的全连接神经网络,可以把解码器输出的向量,映射到一个更大的向量,这个向量称为 logits 向量:假设我们的模型有 10000 个英语单词(模型的输出词汇表),此 logits 向量便会有 10000 个数字,每个数表示一个单词的分数。
- Softmax 层会把这些分数转换为概率(把所有的分数转换为正数,并且加起来等于 1)。然后选择最高概率的那个数字对应的词,就是这个时间步的输出单词。
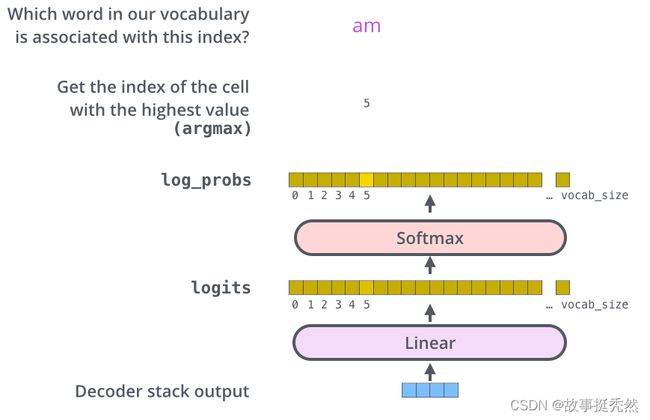
损失函数
Transformer训练的时候,需要将解码器的输出和label一同送入损失函数,以获得loss,最终模型根据loss进行方向传播。
总结
到此Transformer的整个细节进行了学习记录,从编解码模型、注意力机制到自注意力机制的流程进行掌握,从简到难。在transformer中掌握self attention其中的步骤就明白其原理了。
以上是我个人在学习过程中的记录所学,希望对正在一起学习的小伙伴有所帮助!!!
如果对你有帮助,希望你能一键三连【关注、点赞、收藏】!!!
参考链接
The Illustrated Transformer – Jay Alammar – Visualizing machine learning one concept at a time. (jalammar.github.io)
learn-nlp-with-transformers
基于transformers的自然语言处理(NLP)入门