数据结构双向链表
双向链表也叫双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
那么双向链表相对于单项链表就是可以即向后访问又可以向前访问
那么他的结构相对于单链表就复杂很多了
可以看到每一个结点 都有 自己的地址 然后是 指向下一个结点的next域 以及指向上一个地址的prior域
那么在插入删除的时候 我们需要修改更多地方
例如 需要修改我们的 next prior 以及下一个结点的prior和上一个结点的next
而且我们在修改和使用时要考虑到是否存在 next或者prior
那么我们在结构体设计上就要有所不同
#pragma once
//双向链表的结构体设计：
typedef int ELEM_TYPE;
typedef struct DNode
{
ELEM_TYPE data;//数据域
struct DNode *next;//直接后继指针
struct DNode *prior;//直接前驱指针
}DNode, *PDNode;
可实现的操作：
//初始化
void Init_dlist(struct DNode * pdlist);
//头插
bool Insert_head(struct DNode *pdlist, ELEM_TYPE val);
//尾插
bool Insert_tail(struct DNode *pdlist, ELEM_TYPE val);
//按位置插
bool Insert_pos(struct DNode *pdlist, int pos, ELEM_TYPE val);
//头删
bool Del_head(struct DNode *pdlist);
//尾删
bool Del_tail(struct DNode *pdlist);
//按位置删
bool Del_pos(struct DNode *pdlist, int pos);
//按值删
bool Del_val(struct DNode *pdlist, ELEM_TYPE val);
//查找 //查找到，返回的是查找到的这个节点的地址
struct DNode *Search(struct DNode *pdlist, ELEM_TYPE val);
//获取有效值个数
int Get_length(struct DNode *pdlist);
//判空
bool IsEmpty(struct DNode *pdlist);
//清空
void Clear(struct DNode *pdlist);
//销毁1 无限头删
void Destroy1(struct DNode *pdlist);
//销毁2 不借助头结点，有两个辅助指针
void Destroy2(struct DNode *pdlist);
//打印
void Show(struct DNode *pdlist);
我们可以看到 结构体设计时我们需要设计 一个数据域 和 两个指针域
然后其他的实现函数的参数和之前学习的单链表没有什么不同 接下来我们重点看实现代码
首先是初始化
我们只使用next和prior域
void Init_dlist(struct DNode * pdlist)
{
assert(pdlist != NULL);
//pdlist->data 头结点的数据域不使用
pdlist->next = NULL;
pdlist->prior = NULL;
}
我们把他的头节点的next和prior赋值为空
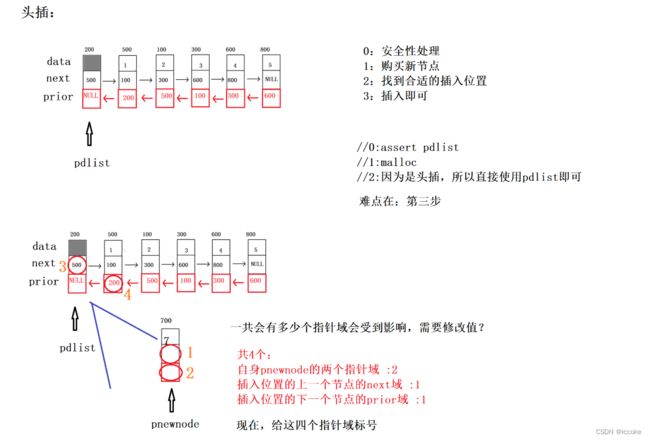
然后是头插
但是头插时我们就要考虑顺序问题和 待插入结点的下一个结点的存在问题
如果我们先修改 待插入结点的上一个结点的next域 那么我们在后续使用时就会因为顺序
产生问题
比如
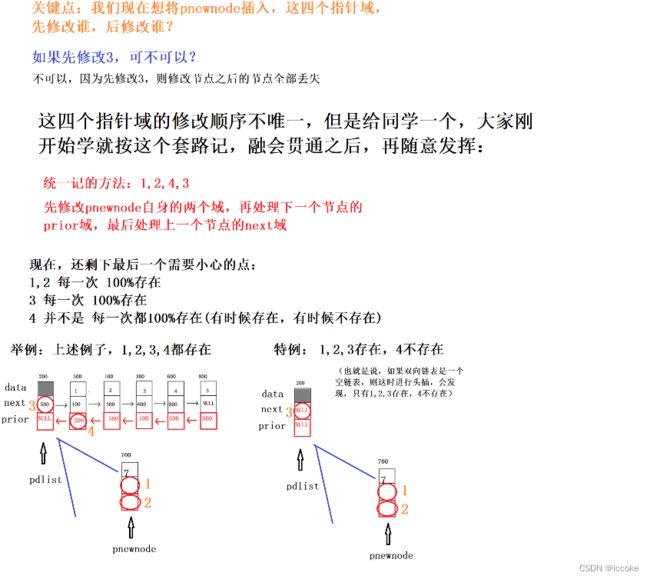因此我们可以调转其他步骤的顺序 但是三号 顺序一定是最后一个
bool Insert_head(struct DNode *pdlist, ELEM_TYPE val)
{
//0.安全性处理
assert(pdlist != NULL);
//1.购买新节点
struct DNode *pnewnode = (struct DNode *)malloc(1 * sizeof(struct DNode));
assert(pnewnode != NULL);
pnewnode->data = val;
//2.找到合适的插入位置(其实就是找到插入在哪一个节点后边，用指针p指向)
//因为是头插，所以直接使用pdlist即可
//3.插入 我们的规则是：1,2,4,3
// 先处理自身的两个指针域(1,2)
// 再处理插入位置的下一个节点的prior域(4)，但是4有特例(空链表进行头插)，不存在
// 最后处理插入位置的上一个节点的next域(3)
pnewnode->next = pdlist->next;//1
pnewnode->prior = pdlist;//2
if(pdlist->next != NULL)//说明不是空链表，则不是特例，4存在
{
//此时，插入位置的下一个节点可以通过pdlist->next访问到，还可以通过pnewnode->next访问到
pdlist->next->prior = pnewnode;//4
//pnewnode->next->prior = pnewnode;//4
}
pdlist->next = pnewnode;
return NULL;
}可以看到 我们实现了第一步和第二步时我们 要判断是否存在四
因为如果不存在四的话 我们对四操作就会变成野指针问题 可能会访问到不能访问的空间 有可能会引发崩溃
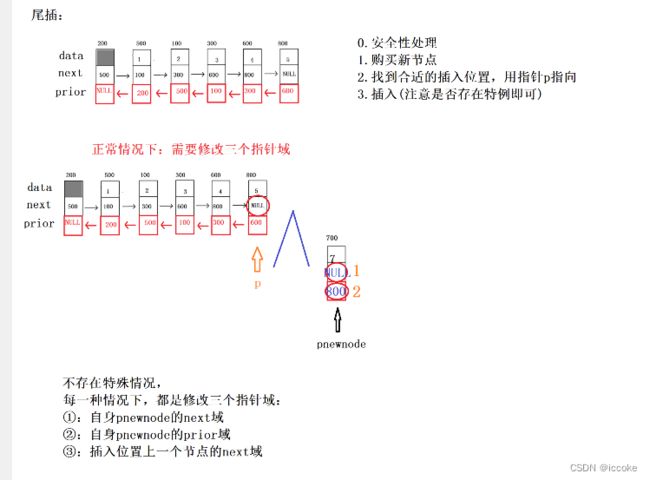
然后是尾插
尾插的话 那么它没有 第四步骤
bool Insert_tail(struct DNode *pdlist, ELEM_TYPE val)
{
//0：
assert(pdlist != NULL);
//1.购买新节点
struct DNode *pnewnode = (struct DNode *)malloc(1 * sizeof(struct DNode));
assert(pnewnode != NULL);
pnewnode->data = val;
//2.找到合适的插入位置,用指针p指向插入位置的前一个节点
//判断是否使用带前驱的for循环
struct DNode *p = pdlist;
for(; p->next!=NULL; p=p->next);
//3.插入（不存在特殊情况，每一种情况都需要修改三个指针域）
//按照之前编号顺序，修改的这三个指针域分别是1,2,(4不存在),3
pnewnode->next = p->next;//pnewnode->next = NULL;//1
pnewnode->prior = p;//2
//4不存在
p->next = pnewnode;//3
return true;
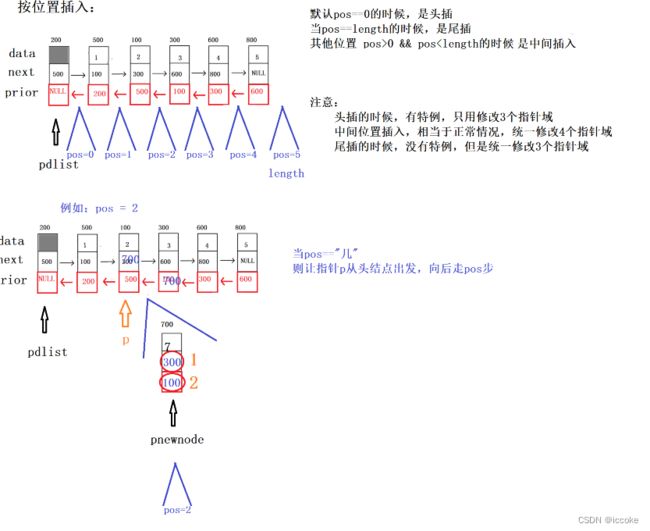
}然后是按位置插入
只要掌握了插入时的顺序问题 在按照函数功能的要求改变即可
bool Insert_pos(struct DNode *pdlist, int pos, ELEM_TYPE val)
{
//因为，在写这个函数之前，头插和尾插已经实现，所以这里可以直接调用
//0.安全性处理
assert(pdlist != NULL);
assert(pos>=0 && pos<=Get_length(pdlist));
//1.分类处理，将头插和尾插的情况，分别调用对应的函数处理
if(pos == 0)//头插
{
return Insert_head(pdlist, val);
}
if(pos == Get_length(pdlist))//尾插
{
return Insert_tail(pdlist, val);
}
//如果既不是头插，也不是尾插，则只有可能是中间插入，1,2,4,3,都存在
//2.剩下来的都是中间位置插入，都正常情况，修改4个指针域
//2.1 购买新节点
struct DNode *pnewnode = (struct DNode *)malloc(1 * sizeof(struct DNode));
assert(pnewnode != NULL);
pnewnode->data = val;
//2.2 找到合适的插入位置，指针p(pos=="几"，指针p从头结点出发向后走pos步)
struct DNode *p = pdlist;
for(int i=0; inext;
}
//2,3 正常插入，1,2,4,3 都存在，4不需要去判断
pnewnode->next = p->next;//1
pnewnode->prior = p;//2
p->next->prior = pnewnode;//4 pnewnode->next->prior = pnownode;
p->next = pnewnode;//3
return true;
} 这里需要注意 根据 位置不同 我们可以直接调用 头插 尾插 和普通插入
然后是删除 在插入和删除前我们都需要判断
但是这里的双向链表没有大小 因此 插入时不需要判满
但是会存在空链表 我们需要在删除时进行 判空操作
bool Del_head(struct DNode *pdlist)
{
//0.安全性处理
assert(pdlist != NULL);
if(IsEmpty(pdlist))
{
return false;
}
//1.用指针p指向待删除节点
struct DNode *p = pdlist->next;
//2.用指针q指向待删除节点的上一个节点
//因为是头删，所以这里指针q用指针pdlist代替
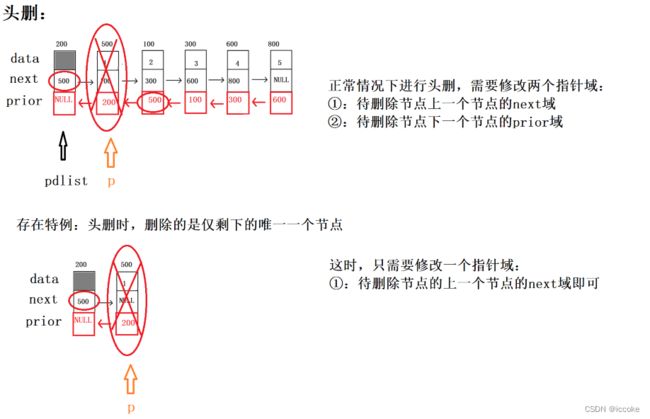
//3.跨越指向(存在特例，正常情况下需要修改两个指针域，而特例时，只需要修改一个指针域)
pdlist->next = p->next;
if(p->next != NULL)//先得判断待删除节点的下一个节点是否存在
{
p->next->prior = pdlist;
}
//4.释放
free(p);
return true;
}
bool IsEmpty(struct DNode *pdlist)
{
return pdlist->next == NULL;
}头删时也存在特列 我们头删时
如果只剩下最后一个结点 我们就只需要改变一个地方即可
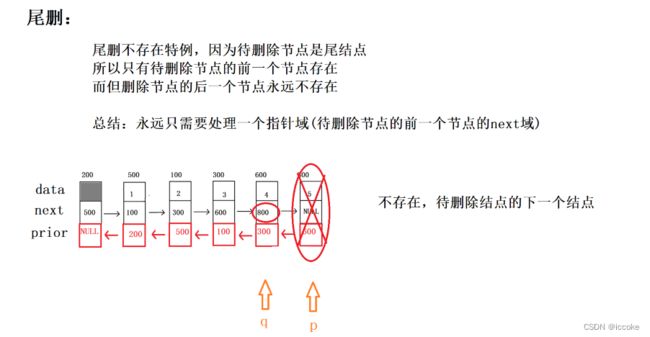
尾删
bool Del_tail(struct DNode *pdlist)
{
//0.
assert(pdlist != NULL);
if(IsEmpty(pdlist))
{
return false;
}
//1.用指针p指向待删除节点
struct DNode *p = pdlist;
for(; p->next!=NULL; p=p->next);
//2.用指针q指向待删除节点的上一个节点
struct DNode *q = pdlist;
for(; q->next!=p; q=q->next);
//3.跨越指向(不存在特例，永远只需要去修改待删除节点的前一个节点的next域)
q->next = p->next;//q->next = NULL;
//4.释放
free(p);
return true;
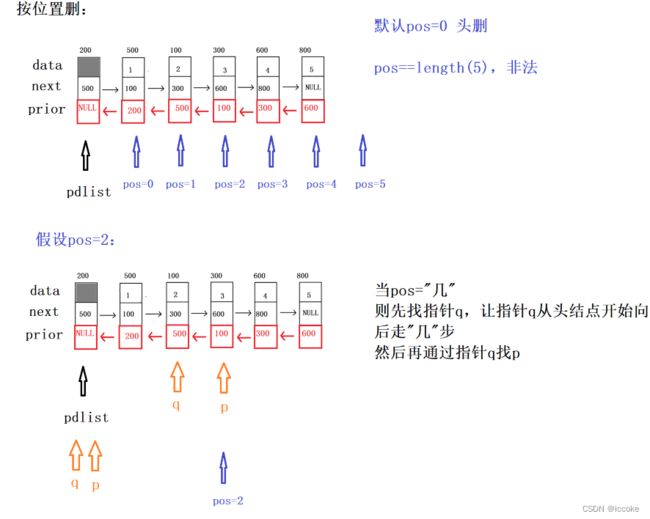
}按位置删除
bool Del_pos(struct DNode *pdlist, int pos)
{
//0.安全性处理
assert(pdlist != NULL);
assert(pos >=0 && posnext;
}
//2.2 找到p，p=q->next
struct DNode *p = q->next;
//2.3 跨越指向+释放
q->next = p->next;
p->next->prior = q;
free(p);
return true;
} 还有个按值删除 然后
bool Del_val(struct DNode *pdlist, ELEM_TYPE val)
{
//0.安全性处理
//1.用指针p指向待删除节点，用search函数
struct DNode *p = Search(pdlist, val);
if(p == NULL)
{
return false;
}
//此时，代码执行到这里，可以保证待删除节点存在，且现在用指针p指向
//2.用指针q指向待删除节点的上一个节点
struct DNode *q = pdlist;
for( ; q->next!=p; q=q->next);
//3.跨越指向(有可能存在特例，例如如果待删除节点是尾结点，则只需要处理一个指针域，反之都是两个)
if(p->next == NULL)//判断待删除节点是否是尾结点
{
q->next = NULL;//q->next = p->next;
}
else//如果待删除节点不是尾结点
{
q->next = p->next;
p->next->prior = q;
}
//4.释放
free(p);
return true;
}
//查找 //查找到，返回的是查找到的这个节点的地址
struct DNode *Search(struct DNode *pdlist, ELEM_TYPE val)
{
//0.安全性处理
//1.判断使用哪种for循环
//使用不需要前驱的for循环
struct DNode *p = pdlist->next;
for(; p!=NULL; p=p->next)
{
if(p->data == val)
{
return p;
}
}
return NULL;
}
还有使用 不带头节点的循环获取有效值个数
int Get_length(struct DNode *pdlist)
{
//assert
//使用不需要前驱的for循环
int count = 0;
struct DNode *p = pdlist->next;
for(; p!=NULL; p=p->next)
{
count++;
}
return count;
}之后依旧是和之前一样的双销毁
void Clear(struct DNode *pdlist)
{
Destroy1(pdlist);
}
//销毁1 无限头删
void Destroy1(struct DNode *pdlist)
{
//assert
while(!IsEmpty(pdlist))
{
Del_head(pdlist);
}
}
//销毁2 不借助头结点，有两个辅助指针
void Destroy2(struct DNode *pdlist)
{
assert(pdlist != NULL);
struct DNode *p = pdlist->next;
struct DNode *q = NULL;
pdlist->next = NULL;
while(p != NULL)
{
q = p->next;
free(p);
p = q;
}
}完整代码
#include
#include
#include
#include "dlist.h"
可实现的操作：
//初始化
void Init_dlist(struct DNode * pdlist)
{
assert(pdlist != NULL);
//pdlist->data 头结点的数据域不使用
pdlist->next = NULL;
pdlist->prior = NULL;
}
//头插
bool Insert_head(struct DNode *pdlist, ELEM_TYPE val)
{
//0.安全性处理
assert(pdlist != NULL);
//1.购买新节点
struct DNode *pnewnode = (struct DNode *)malloc(1 * sizeof(struct DNode));
assert(pnewnode != NULL);
pnewnode->data = val;
//2.找到合适的插入位置(其实就是找到插入在哪一个节点后边，用指针p指向)
//因为是头插，所以直接使用pdlist即可
//3.插入 我们的规则是：1,2,4,3
// 先处理自身的两个指针域(1,2)
// 再处理插入位置的下一个节点的prior域(4)，但是4有特例(空链表进行头插)，不存在
// 最后处理插入位置的上一个节点的next域(3)
pnewnode->next = pdlist->next;//1
pnewnode->prior = pdlist;//2
if(pdlist->next != NULL)//说明不是空链表，则不是特例，4存在
{
//此时，插入位置的下一个节点可以通过pdlist->next访问到，还可以通过pnewnode->next访问到
pdlist->next->prior = pnewnode;//4
//pnewnode->next->prior = pnewnode;//4
}
pdlist->next = pnewnode;
return NULL;
}
//尾插
bool Insert_tail(struct DNode *pdlist, ELEM_TYPE val)
{
//0：
assert(pdlist != NULL);
//1.购买新节点
struct DNode *pnewnode = (struct DNode *)malloc(1 * sizeof(struct DNode));
assert(pnewnode != NULL);
pnewnode->data = val;
//2.找到合适的插入位置,用指针p指向插入位置的前一个节点
//判断是否使用带前驱的for循环
struct DNode *p = pdlist;
for(; p->next!=NULL; p=p->next);
//3.插入（不存在特殊情况，每一种情况都需要修改三个指针域）
//按照之前编号顺序，修改的这三个指针域分别是1,2,(4不存在),3
pnewnode->next = p->next;//pnewnode->next = NULL;//1
pnewnode->prior = p;//2
//4不存在
p->next = pnewnode;//3
return true;
}
//按位置插
bool Insert_pos(struct DNode *pdlist, int pos, ELEM_TYPE val)
{
//因为，在写这个函数之前，头插和尾插已经实现，所以这里可以直接调用
//0.安全性处理
assert(pdlist != NULL);
assert(pos>=0 && pos<=Get_length(pdlist));
//1.分类处理，将头插和尾插的情况，分别调用对应的函数处理
if(pos == 0)//头插
{
return Insert_head(pdlist, val);
}
if(pos == Get_length(pdlist))//尾插
{
return Insert_tail(pdlist, val);
}
//如果既不是头插，也不是尾插，则只有可能是中间插入，1,2,4,3,都存在
//2.剩下来的都是中间位置插入，都正常情况，修改4个指针域
//2.1 购买新节点
struct DNode *pnewnode = (struct DNode *)malloc(1 * sizeof(struct DNode));
assert(pnewnode != NULL);
pnewnode->data = val;
//2.2 找到合适的插入位置，指针p(pos=="几"，指针p从头结点出发向后走pos步)
struct DNode *p = pdlist;
for(int i=0; inext;
}
//2,3 正常插入，1,2,4,3 都存在，4不需要去判断
pnewnode->next = p->next;//1
pnewnode->prior = p;//2
p->next->prior = pnewnode;//4 pnewnode->next->prior = pnownode;
p->next = pnewnode;//3
return true;
}
//头删 //这里写的也要注意，也存在特例
bool Del_head(struct DNode *pdlist)
{
//0.安全性处理
assert(pdlist != NULL);
if(IsEmpty(pdlist))
{
return false;
}
//1.用指针p指向待删除节点
struct DNode *p = pdlist->next;
//2.用指针q指向待删除节点的上一个节点
//因为是头删，所以这里指针q用指针pdlist代替
//3.跨越指向(存在特例，正常情况下需要修改两个指针域，而特例时，只需要修改一个指针域)
pdlist->next = p->next;
if(p->next != NULL)//先得判断待删除节点的下一个节点是否存在
{
p->next->prior = pdlist;
}
//4.释放
free(p);
return true;
}
//尾删
bool Del_tail(struct DNode *pdlist)
{
//0.
assert(pdlist != NULL);
if(IsEmpty(pdlist))
{
return false;
}
//1.用指针p指向待删除节点
struct DNode *p = pdlist;
for(; p->next!=NULL; p=p->next);
//2.用指针q指向待删除节点的上一个节点
struct DNode *q = pdlist;
for(; q->next!=p; q=q->next);
//3.跨越指向(不存在特例，永远只需要去修改待删除节点的前一个节点的next域)
q->next = p->next;//q->next = NULL;
//4.释放
free(p);
return true;
}
//按位置删
bool Del_pos(struct DNode *pdlist, int pos)
{
//0.安全性处理
assert(pdlist != NULL);
assert(pos >=0 && posnext;
}
//2.2 找到p，p=q->next
struct DNode *p = q->next;
//2.3 跨越指向+释放
q->next = p->next;
p->next->prior = q;
free(p);
return true;
}
//按值删
bool Del_val(struct DNode *pdlist, ELEM_TYPE val)
{
//0.安全性处理
//1.用指针p指向待删除节点，用search函数
struct DNode *p = Search(pdlist, val);
if(p == NULL)
{
return false;
}
//此时，代码执行到这里，可以保证待删除节点存在，且现在用指针p指向
//2.用指针q指向待删除节点的上一个节点
struct DNode *q = pdlist;
for( ; q->next!=p; q=q->next);
//3.跨越指向(有可能存在特例，例如如果待删除节点是尾结点，则只需要处理一个指针域，反之都是两个)
if(p->next == NULL)//判断待删除节点是否是尾结点
{
q->next = NULL;//q->next = p->next;
}
else//如果待删除节点不是尾结点
{
q->next = p->next;
p->next->prior = q;
}
//4.释放
free(p);
return true;
}
//查找 //查找到，返回的是查找到的这个节点的地址
struct DNode *Search(struct DNode *pdlist, ELEM_TYPE val)
{
//0.安全性处理
//1.判断使用哪种for循环
//使用不需要前驱的for循环
struct DNode *p = pdlist->next;
for(; p!=NULL; p=p->next)
{
if(p->data == val)
{
return p;
}
}
return NULL;
}
//获取有效值个数
int Get_length(struct DNode *pdlist)
{
//assert
//使用不需要前驱的for循环
int count = 0;
struct DNode *p = pdlist->next;
for(; p!=NULL; p=p->next)
{
count++;
}
return count;
}
//判空
bool IsEmpty(struct DNode *pdlist)
{
return pdlist->next == NULL;
}
//清空
void Clear(struct DNode *pdlist)
{
Destroy1(pdlist);
}
//销毁1 无限头删
void Destroy1(struct DNode *pdlist)
{
//assert
while(!IsEmpty(pdlist))
{
Del_head(pdlist);
}
}
//销毁2 不借助头结点，有两个辅助指针
void Destroy2(struct DNode *pdlist)
{
assert(pdlist != NULL);
struct DNode *p = pdlist->next;
struct DNode *q = NULL;
pdlist->next = NULL;
while(p != NULL)
{
q = p->next;
free(p);
p = q;
}
}
//打印
void Show(struct DNode *pdlist)
{
//assert
//使用不需要前驱的for循环
struct DNode *p = pdlist->next;
for(; p!=NULL; p=p->next)
{
printf("%d ", p->data);
}
printf("\n");
}