C语言复习整理（十三）——指针与链表

指针与链表

链表，首先可以细分为一小块一小块的结构体变量，这一小块一小块的结构体变量在链表中是首尾相连的顾名思义 就像一条铁链一样 而这每一小块的结构体变量中又可以从大方向地分成两个部分， 其中一个部分就是——涵盖着该结构体变量里的所有信息，另一个部分就是链接每块结构体变量的部分——指针。
链表的特点：用时申请，不用时释放，插入和删除只需少量操作，能大大提高空间利用率和时间效率。
在链表中，有一个头指针变量，只保存一个地址，头指针指向一个变量，称为元素。在链表中，每一个元素包含两部分：数据部分和指针部分。数据部分用来存放元素所包含的数据，指针部分用来指向下一个元素。最后一个元素的指针指向NULL，表示指向的地址为空（链尾）。

**静态链表：**把线性表的元素存放在数组中，这些元素可能在物理上是连续存放的，也可能不是连续的，他们之间通过逻辑关系来连接。数组单元存放链表节点，结点的链域指向下一个元素的位置，即下一个元素所在的数组单元的下标。静态链表需要用数组来实现。
**动态链表：**在执行过程中从无到有地建立起一个链表，即一个一个地开辟结点和输入各结点的数据，并建立起前后相连的关系。

单链表

在链表中，每个结点只有一个指针，所有的结点都是单线联系，除了末尾结点指针为空外，每个指针都指向下一结点单链表，一环扣一环形成一条线性链，即为单链表。

单链表的特点：
（1）有一个head指针变量，它存放第一个节点的地址，称为头指针。
（2）每个节点都包含一个数据域和指针域，数据域存放数据，指针域存放下一个节点的地址。从头指针head开始，head指向第一个节点，第一个节点指向第二个节点…直到最后一个节点。所有节点都是单线联系。
（3）最后一个节点不再指向其他节点，称为尾节点，指针域为空指针NULL。表示链表到此结束，指向表尾的指针称为尾指针。
（4）链表各结点之间的顺序关系由指针域来确定，不要求逻辑相连的结点在物理地址上也相连。即链表依靠指针相连不需要占用一片连续的内存空间。
（5）随着处理数据的增加，链表可以不受程序中变量定义的限制无限的延长（仅受内存总量的限制）。在插入和删除操作中，只需要修改相关结点的指针域的链接关系，不需要像数组那样大量给变数据的实际存储位置。

缺点：
1、比顺序存储结构的存储密度小 (每个节点都由数据域和指针域组成，所以相同空间内假设全存满的话顺序比链式存储更多)。
2、查找结点时链式存储要比顺序存储慢（每个节点地址不连续、无规律，导致按照索引查询效率低下）。
优点：
1、插入、删除灵活 (不必移动节点，只要改变节点中的指针，但是需要先定位到元素上)。
2、有元素才会分配结点空间，不会有闲置的结点。

typedef int ElemType,Status;
typedef struct LNode{
	ElemType data;
	struct LNode * next;
}LNode,*LinkList;

主要操作：
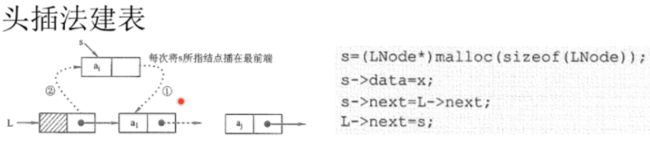
1.创建（头插法）

Status CreateList_H(LinkList & L,int n)
{
	L = (LinkList)malloc(sizeof(LNode));
	LNode * s;
	L->next = NULL;
	int i;
	ElemType ele;
	for(i = 0;i < n;i++)
	{
		scanf("%d",&ele);
		s = (LNode*)malloc(sizeof(LNode));		
		s->data = ele;
		s->next = L->next;
		L->next = s;
	}
	return OK;
} 

2.创建（尾插法）

Status CreateList_T(LinkList &L,int n)
{
	L = (LinkList)malloc(sizeof(LNode));
	L->next = NULL;
	LNode * s;
	LNode * r = L;
	int i;
	ElemType ele;
	for(i = 0;i < n;i++)
	{
		scanf("%d",&ele);
		s = (LNode*)malloc(sizeof(LNode));		
		s->data = ele;
		r->next = s;
		r = s;
	}
	r->next = NULL;
	return OK;
} 

3.按值查找

LNode * GetList_Elem(LinkList L,ElemType find_ele)
{
	LNode * node = L->next;
	while(node!=NULL && node->data != find_ele)
	{
		node = node->next;
	}
	return node;
}

4.按位置查找

LNode * GetList_Pos(LinkList L,int pos)
{
	if(pos == 0)
	{
		return L;
	}
	if(pos < 1)
	{
		return NULL;
	}
	LNode * node = L;
	int j = 0;
	while(node && j < pos)
	{
		
		node =node->next;
		j++;
	}
	if(node == NULL)
	{
		printf("插入位置超出范围！");
		return NULL;	
	}
	return node;
}

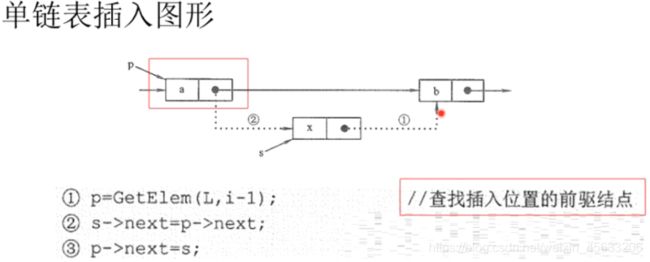
5.指定位置插入

Status InserElem(LinkList & L,int pos,ElemType inser_ele)
{
	LNode * node;
	LNode * new_node = (LNode*)malloc(sizeof(LNode));
	new_node->data = inser_ele;
	node = GetList_Pos(L,pos-1);//查找到当前结点的前驱结点
	new_node->next = node->next;//插入结点指向前驱结点的next
	node->next = new_node;//前驱结点的next指向插入结点
	return OK;
}
/*
node->next = new_node;
new_node->next = node->next;
不能这样写！！！
如果先将前驱结点的next指向插入结点，原先链表的后续结点就失去了逻辑上的指向，找不到了。
而且这样写的话第二句程序就变成了插入结点的后继指向了前驱结点的后继，即自己指向了自己。
*/

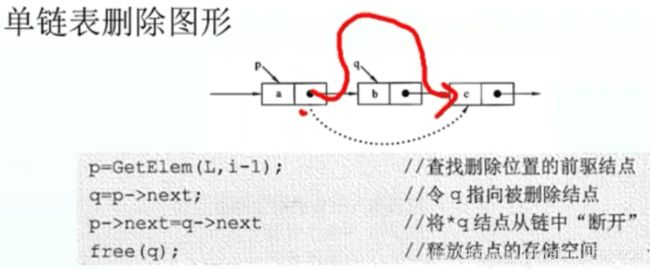
6.指定位置删除

Status DeleteElem(LinkList & L,int pos)
{
	LNode * node;
	LNode *del_node;
	node = GetList_Pos(L,pos-1);//找到待删除结点的前驱结点
	del_node = node->next;//用一个链表指针指向删除结点
	node->next = del_node->next;//前驱结点指向待删除结点的后继结点（此时在逻辑上已删除）
	free(del_node);//释放待删除结点所占的内存空间（至此，在逻辑与物理上都删除了该节点）
	return OK;
} 
//一定要记得free掉待删除结点，不free的话，好的情况只是占用了内存，坏情况成为野指针造成内存泄漏

7.输出链表

void PrintList(LinkList L)
{
	LNode * node = L->next;
	printf("表中元素为:\n"); 
	while(node!= NULL)
	{
		printf("%d\t",node->data);
		node = node->next;
	} 
	printf("\n\n");
}

8.合并两个升序链表（合并后仍保持升序）

void MergeList(LinkList & LA,LinkList & LB,LinkList & LC)
{
	LNode * anode = LA->next;
	LNode * bnode = LB->next;
	LNode * cnode;
	LC = cnode = LA;
	while(anode!= NULL && bnode !=NULL)
	{
		if(anode->data <= bnode->data)
		{
			cnode->next = anode;
			cnode = anode;
			anode = anode->next;
		}
		else
		{
			cnode->next = bnode;
			cnode = bnode;
			bnode = bnode->next;
		}	
	}
	cnode->next = anode?anode:bnode;
	free(LB);
} 

主函数测试：

int main()
{
	LinkList L;
	ElemType inser_ele;
	LNode * find_node;
	ElemType del_ele;
	int pos;
	printf("初始化链表L，请输入5个数字："); 
	CreateList_T(L,5);
	PrintList(L);
	printf("请输入要插入的元素以及插入的位置:(用逗号隔开，输入法为英文)");
	scanf("%d,%d",&inser_ele,&pos);
	InserElem(L,pos,inser_ele); 
	PrintList(L);
	printf("请输入要删除元素的位置：");
	scanf("%d",&pos);
	DeleteElem(L,pos); 
	PrintList(L);
	printf("请输入要查找的元素的位置：");
	scanf("%d",&pos);
	find_node = GetList_Pos(L,pos);
	printf("所查找的元素为:%d\n",find_node->data); */
	printf("------接下来为单链表的合并---------\n");
	LinkList LA; 
	LinkList LB; 
	LinkList LC; 
	printf("初始化链表LA，请输入5个数字："); 
	CreateList_T(LA,5);
	printf("初始化链表LB，请输入5个数字："); 
	CreateList_T(LB,5);
	CreateList_T(LC,0);
	MergeList(LA,LB,LC);
	PrintList(LC);
	return 0;
}

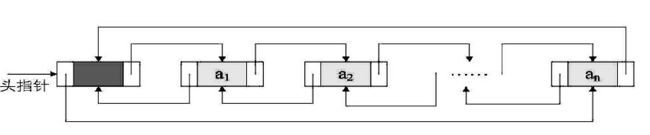
循环链表

头节点和尾节点被连接在一起的链表称为循环链表，这种方式在单向和双向链表中皆可实现。循环链表中第一个节点之前就是最后一个节点，反之亦然。

尾插法创建单向循环链表：

typedef struct LNode
{
    int data;
    struct LNode *next;
}*CircleLinkedList,LNode;
 
void CreatLinkedList(CircleLinkedList &L,int n)   //尾插法创建循环链表;
{
    L = (CircleLinkedList)malloc(sizeof(LNode));  //初始化;
    L->next = NULL;
    L->data = 0;
    CircleLinkedList Tail = L;    //尾指针;
    cout<<"Enter "<<n<<" number(s)"<<endl;
    for(int i = 0 ; i < n; i++)
    {
        CircleLinkedList Temp = (CircleLinkedList)malloc(sizeof(LNode));
        cin>>Temp->data;
        Tail->next = Temp;
        Tail = Temp;
        L->data++;
    }
    Tail->next = L;
}

双向循环链表如下图：

双向链表

要在单向链表中找到某个节点的前驱节点，必须从链表的头节点出发依次向后寻找，但是需要Ο(n)时间。为此我们可以扩展单向链表的节点结构，使得通过一个节点的引用，不但能够访问其后续节点，也可以方便的访问其前驱节点。扩展单向链表节点结构的方法是，在单链表节点结构中新增加一个域，该域用于指向节点的直接前驱节点。该链表称为双向链表。单向链表只能从一个方向遍历，双向链表可以从两个方向遍历。

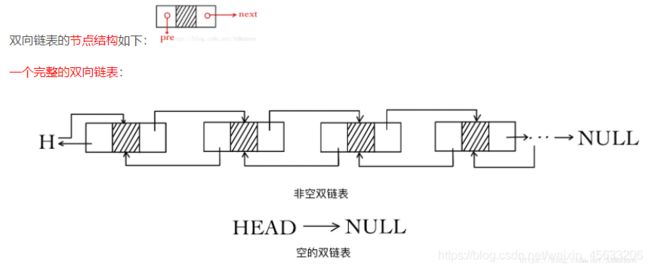
typedef struct LNode
{
    int data;
    struct LNode *pre;
    struct LNode *next;
}*DoubleLinkedList,LNode;

在使用双向链表实现链接表时，为使编程更加简洁，我们使用带两个哑元节点的双向链表来实现链接表。其中一个是头节点，另一个是尾节点，它们都不存放数据元素，头节点的pre 为空，而尾节点的 Next 为空。

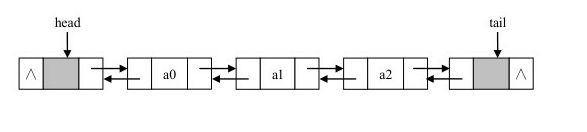
在具有头尾节点的双向链表中插入和删除节点，无论插入和删除的节点位置在何处，因为首尾节点的存在，插入、删除操作都可以被归结为某个中间节点的插入和删除；并且因为首尾节点的存在，整个链表永远不会为空，因此在插入和删除节点之后，也不用考虑链表由空变为非空或由非空变为空的情况下 head 和 tail 的指向问题；从而简化了程序。

void CreatDoubleLinkedList(DoubleLinkedList &L,int n)   //尾插法创建双链表;
{
    L = (DoubleLinkedList)malloc(sizeof(LNode));
    L->pre = NULL;
    L->next = NULL;
    L->data = 0;
    DoubleLinkedList Tail = L;
    cout<<"Enter "<<n<<" Elem(s) :"<<endl;
    for(int i = 0; i < n; i++)
    {
        DoubleLinkedList Temp = (DoubleLinkedList)malloc(sizeof(LNode));
        cin>>Temp->data;
        Tail->next = Temp;
        Temp->pre = Tail;
        Tail = Temp;
        L->data++;
    }
    Tail->next = NULL;
}

双向链表的数据元素插入原理：

若想在第i个位置上插入数据，则先遍历到第i-1个位置，使用malloc()函数向系统请求一个新节点T

    1.让T->pre 指向 第i-1个节点；
    2.让T->next 指向 第i-1个结点的下一个节点(即第i个节点);
    3.让i->next 指向 T;
    4.让i->pre指向T；(前提是第i个节点非空)

bool InsertElem(int e,int i,DoubleLinkedList L)    //插入结点;
{
    if(i > L->data+1 || i < 1)
        return false;
    else
    {
        L->data++;
        while(i > 1)
        {
            L = L->next;
            i--;
        }
        DoubleLinkedList Temp = (DoubleLinkedList)malloc(sizeof(LNode));
        Temp->data = e;
        if(L->next != NULL)
        {
            Temp->next = L->next;
            Temp->pre = L;
            L->next->pre = Temp;
            L->next = Temp;
        }
        else
        {
            Temp->pre = L;
            L->next = Temp;
            Temp->next = NULL;
        }
    }
}

双向链表的数据元素删除原理：

若想在第i个位置上插入数据，则先遍历到第i-1个位置，使用malloc()函数向系统请求一个新节点P，且让P指向第i个数据

        1.让P->next->pre 指向 P->pre；(前提是第i+1个节点非空)
        2.让i->next 指向 p->next;
        3.释放P节点所占用的空间；(即删除了第i个节点)

bool DeleteElem(int i,DoubleLinkedList L)   //删除结点;
{
    if(i > L->data || i < 1)
        return false;
    else
    {
        L->data--;
        while(i > 1)
        {
            L = L->next;
            i--;
        }
        DoubleLinkedList Temp = (DoubleLinkedList)malloc(sizeof(LNode));
        Temp = L->next;
        if(L->next->next != NULL)
        {
            L->next->next->pre = L;
            L->next = L->next->next;
        }
        else
            L->next = NULL;
        free(Temp);
        Temp = NULL;
        return true;
    }
}