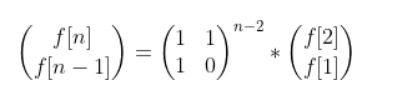Fibonacci 第 n 项和Fibonacci 前 n 项和（快速幂+矩阵乘法）

Fibonacci 第 n 项（快速幂+矩阵乘法）

题目描述
大家都知道 Fibonacci 数列吧，f1=1,f2=1,f3=2,f=3…fn=fn-1+fn-2,
f1=1,f2=1,f3=2,f4=3,…,fn=fn−1+fn−2。
现在问题很简单，输入 n 和 m，求 fn mod m

输入格式
输入 n,m。

输出格式
输出 fn mod m

样例输入
5 1000

样例输出
5

数据范围与提示
对于 100% 的数据， 1≤n≤2×10⁹,1≤m≤10⁹+10。

思路： 这个题数据范围很大，暴力肯定是不行的，所以这里计算用到了矩阵乘法和快速幂

显而易见

f[i]   = 1 * f[i-1] + 1 * f[i-2]
f[i-1] = 1 * f[i-1] + 0 * f[i-2]

即可得

同理可得

化简后为

矩阵的n-2次方，用快速幂计算，算出来还是一个2*2的矩阵，我们设为矩阵g，又f[2]=f[1]=1，故f[n]=g[1][1]+g[1][2]

AC代码：

#include
#include
#include
#define ll long long
using namespace std;
int n,m;
struct node
{
	ll a[10][10];
} p,g;
void init(node &x)//单位矩阵
{
	for(int i=1; i<=2; i++)
		for(int j=1; j<=2; j++)
		{
			if(i==j)
				x.a[i][j]=1;
			else
				x.a[i][j]=0;
		}
}
void mul(node &x,node &y,node &t)//矩阵乘法（把矩阵x乘以矩阵y的结果储存到矩阵t）
{
	memset(t.a,0,sizeof(t.a));
	for(int i=1; i<=2; i++)
		for(int j=1; j<=2; j++)
			for(int k=1; k<=2; k++)
			{
				t.a[i][j]+=x.a[i][k]*y.a[k][j];
				t.a[i][j]%=m;
			}
}
void ksm(int k)//快速幂
{
//矩阵g存最终答案
//矩阵ff存底数
//mul（i,j,t）矩阵i和矩阵j相乘的答案存在矩阵t中
	init(g);
	node t,ff=p;
	while(k)
	{
		if(k%2)
			mul(g,ff,t),g=t;//g=g*ff;//答案*底数的一次幂
		mul(ff,ff,t),ff=t;//ff=ff*ff;//底数加倍
		k/=2;
	}
}
int main()
{
	int i,j,k;
	scanf("%d%d",&n,&m);
	p.a[1][1]=1;//初始2*2矩阵的值
	p.a[1][2]=1;
	p.a[2][1]=1;
	p.a[2][2]=0;
	if(n<=2)
		printf("1\n");
	else
	{
		ksm(n-2);
		ll ans=(g.a[1][1]%m+(g.a[1][2]%m))%m;
		printf("%lld\n",ans);
	}
	return 0;
}

Fibonacci 前 n 项和

题目描述
大家都知道 Fibonacci 数列吧，f1=1,f2=1,f3=2,f=3…fn=fn-1+fn-2,
f1=1,f2=1,f3=2,f4=3,…,fn=fn−1+fn−2。
现在问题很简单，输入 n 和 m，求 {fn}的前n项sn mod m

输入格式
输入 n,m。

输出格式
输出 fn mod m

样例输入
5 1000

样例输出
12

思路：

可得 f[n] = f[n-1] + f[n-2] ;

移项 f[n-2] = f[n] - f[n-1] ;

令n=n+2
f[n] = f[n+2] - f[n+1] ;

则有
f[1] = f[3] - f[2] ;
f[2] = f[4] - f[3] ;
f[3] = f[5] - f[4] ;
...
f[n] = f[n+2] - f[n+1] ;

各项相加得s[n] = f[n+2] -f[2] = f[n+2] - 1 ;

故可直接套上个题得板子，稍微修改即可

AC代码：

#include
#include
#include
#define ll long long
using namespace std;
int n,m;
struct node
{
	ll a[10][10];
} p,g;
void init(node &x)//单位矩阵
{
	for(int i=1; i<=2; i++)
		for(int j=1; j<=2; j++)
		{
			if(i==j)
				x.a[i][j]=1;
			else
				x.a[i][j]=0;
		}
}
void mul(node &x,node &y,node &t)//矩阵乘法（把矩阵x乘以矩阵y的结果储存到矩阵t）
{
	memset(t.a,0,sizeof(t.a));
	for(int i=1; i<=2; i++)
		for(int j=1; j<=2; j++)
			for(int k=1; k<=2; k++)
			{
				t.a[i][j]+=x.a[i][k]*y.a[k][j];
				t.a[i][j]%=m;
			}
}
void ksm(int k)//快速幂
{
//矩阵g存最终答案
//矩阵ff存底数
//mul（i,j,t）矩阵i和矩阵j相乘的答案存在矩阵t中
	init(g);
	node t,ff=p;
	while(k)
	{
		if(k%2)
			mul(g,ff,t),g=t;//g=g*ff;//答案*底数的一次幂
		mul(ff,ff,t),ff=t;//ff=ff*ff;//底数加倍
		k/=2;
	}
}
int main()
{
	int i,j,k;
	scanf("%d%d",&n,&m);
	p.a[1][1]=1;
	p.a[1][2]=1;
	p.a[2][1]=1;
	p.a[2][2]=0;
	if(n<=2)
		printf("1\n");
	else
	{
		ksm(n);//f[n]求n-2次方，f[n+2]求n次方
		ll ans=(g.a[1][1]%m+(g.a[1][2]%m))%m;
		printf("%lld\n",ans-1);//f[n+2]-1
	}
	return 0;
}