张量学习（1）：张量的基本概念

1.张量的四种定义

1.张量是多维数组，这个定义常见于各种人工智能软件。
2.张量是某种几何对象，不会随着坐标系的改变而改变
3.张量是向量和余向量（covector）通过张量积（tensor product）组合而成的。
4.张量是多重线性映射，即：


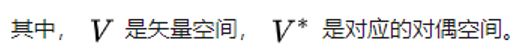
除零阶张量外，张量的具体表示还与坐标系的选择有关，选择不同的坐标系，意味着选择不同的基矢（basis）进行展开。以矢量为例，在给定坐标系，矢量由多个数构成，这些数实际上为当前基矢下的展开系数，如果坐标轴变化了，即基矢变化了，那么自然而然，对应的展开系数也就变化了。

2.张量表示形式

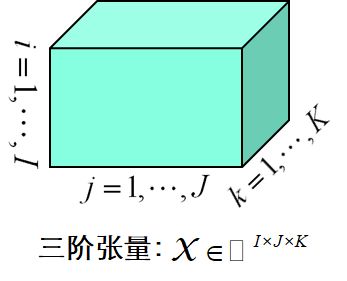
一阶张量可以理解为一个向量，二阶张量可以理解为矩阵，三阶张量可以理解成立方体，四阶张量可以理解成立方体组成的一个向量，五阶张量可以理解成立方体组成的矩阵，依次类推。
把三维张量画成一个立方体：

3.现实世界中的数据张量

1）向量数据

2D张量，形状为（samples,features）

2）时间序列数据或序列数据

3D张量，形状为（sampels,timesteps,features）

当时间（或序列顺序）对于数据很重要时，应该将数据存储在带有时间轴的3D张量中。每个样本可以被编码为一个向量序列（即2D张量），因此一个数据批量就被编码为一个3D张量。

图像通常具有三个维度：高度，宽度和颜色深度。虽然灰度图像（比如MNIST数字图像）只有一个颜色通道，因此可以保存在2D张量中，但按照惯例，图像张量始终是3D张量，灰度图像的彩色通道只有一维。因此，如果图像大小为 $256\times 256$ ，那么128张灰度图像组成的批量可以保存在一个形状为（128，256，256，1）的张量中，而128张彩色图像组成的批量则可以保存在一个形状为（128，256，256，3）的张量中。

图像张量的形状有两种约定：通道在后（channels-last）的约定（在 TensorFlow 中使用）和 通道在前（channels-first）的约定（在 Theano 中使用）。Google 的 TensorFlow 机器学习框架将 颜色深度轴放在最后：(samples, height, width, color_depth)。与此相反，Theano 将图像深度轴放在批量轴之后：(samples, color_depth, height, width)。如果采 用 Theano 约定，前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)。 Keras 框架同时支持这两种格式。

3）图像

4D张量，形状为（samples,height,width,channels）或（samples,channels,height,width）

4）视频

5D张量，形状为（samples,frames,height,width,channels）或（samples,frames,channels,height,width）

视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧， 每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_ depth) 的 3D 张量中，因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中，而不同视频组成的批量则可以保存在一个 5D 张量中，其形状为 (samples, frames, height, width, color_depth)。

4）阶（order/ways/modes/rank）

阶：张成所属张量空间的向量空间的个数
一阶张量（向量）：[5,10,15,30,25]
二阶张量（矩阵）：（[[5,10,15,30,25],[20,30,65,70,90],[7,80,95,20,30]]）
三阶张量：（[[[5,10,15,30,25],[20,30,65,70,90],[7,80,95,20,30]],[[3,1,1,0,2],[2,3,5,7,9],[7,8,5,2,3]],[[15,0,5,0,5],[0,0,5,0,0],[7,0,5,0,0]]]）

在实际的操作中，秩可以理解为[的深度。例如：
rank = 1:[0,1,2]
rank = 2:[[0,1],[2,3]]
rank = 3:[[[0,1],[2,3]],[[4,5],[6,7]]]

一阶张量（向量）：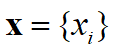
二阶张量（矩阵）：

三阶或更高阶张量：
零阶张量（数量）：

以三阶张量为例：

个人思考：

1.疑问：什么是对偶空间？

那么$V^{\ast }$也是向量空间，这个空间称为$V$的对偶空间

2.疑问：什么是张成所属张量空间的向量空间？

这句话的意思应该是 张成 张量空间中的向量空间 。缩句：张成XX的向量空间。
那什么叫张成向量空间？
官方的解释：向量的张成就是线性张成，指的是一些向量的所有线性组合构成的一个集合（显然是一个线性空间，其一组基为该向量组的极大无关组）

所以，阶的解释“张成所属张量空间的向量空间的个数” 等价于“一个张量空间的向量空间的极大无关组中的向量个数”

以上疑问的解答可能仍然有错误之处，可能在后面学习过程中不断的改正。