透视投影矩阵推导
透视投影矩阵(Perspective Projection Matrix)的作用是进行规范化透视投影变换,即 观察空间 → \rightarrow →规范化观察空间。
在OpenGL中,传给 projectionMatrix 的值:
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);

近截面与远截面之间构成的四棱台称为棱台观察体,而透视投影矩阵的任务就是把位于观察体内的物体的顶点 x , y , z x,y,z x,y,z 坐标映射到 [ − 1 , 1 ] [-1,1] [−1,1] 范围。这相当于把这个四棱台扭曲变形成一个立方体。这个立方体叫做规范化观察体(Normalized View Volume)。

矩阵的形式
在投影中心位于原点且观察平面在近裁剪平面位置时,有
M p e r s , n o r m = ( 1 a s p e c t ⋅ tan ( f o v y 2 ) 0 0 0 0 1 tan ( f o v y 2 ) 0 0 0 0 z N e a r + z F a r z N e a r − z F a r 2 ⋅ z N e a r ⋅ z F a r z N e a r − z F a r 0 0 − 1 0 ) M_{pers,norm}=\begin{pmatrix} \frac{1}{aspect\cdot\tan(\frac{fovy}{2})} & 0 &0&0\\ 0&\frac{1}{\tan(\frac{fovy}{2})}&0&0\\ 0&0&\frac{zNear+zFar}{zNear-zFar}&\frac{2\cdot zNear\cdot zFar}{zNear-zFar}\\ 0&0&-1&0\\ \end{pmatrix} Mpers,norm=⎝⎜⎜⎜⎛aspect⋅tan(2fovy)10000tan(2fovy)10000zNear−zFarzNear+zFar−100zNear−zFar2⋅zNear⋅zFar0⎠⎟⎟⎟⎞
其中的 1 tan ( f o v y 2 ) \frac{1}{\tan(\frac{fovy}{2})} tan(2fovy)1 可化为 cot ( f o v y 2 ) \cot(\frac{fovy}{2}) cot(2fovy)
参数
fovy:摄像机垂直方向的 FOV(Field of View,视场角),相机可以接收影像的角度范围,也可以称为视野;aspect:裁剪平面的宽高比;zNear:摄像机与近裁剪平面的距离;zFar:摄像机与远裁剪平面的距离。
三维观察流水线
投影变换
对象描述变换到观察坐标后,下一阶段是将其投影到观察平面上。图形软件一般都支持平行投影和透视投影两种方式。
-
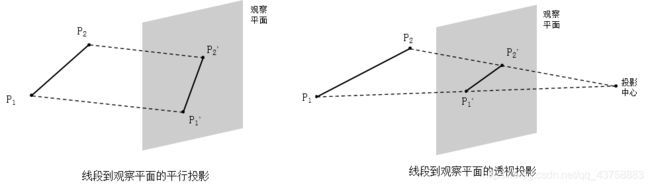
在平行投影(parallel projection)中,坐标位置沿平行线变换到观察平面上。下图给出了用端点坐标 P 1 P_1 P1和 P 2 P_2 P2描述的线段的平行投影。平行投影保持对象的有关比例不变,这是三维对象计算机辅助绘图和设计中产生成比例工程图的方法。场景中的平行线在平行投影中显示成平行的。一般有两种获得对象平行视图的方法:沿垂直于观察平面的直线投影,或沿某倾斜角度投影到观察平面。
-
在透视投影(perspective projection)中,对象位置沿 会聚到观察平面后一点的直线 变换到投影坐标系。下图给出了使用端点坐标 P 1 P_1 P1和 P 2 P_2 P2描述的线段的透视投影。与平行投影不同的是,透视投影不保持对象的相关比例。但场景的透视投影真实感较好,因为在透视显示中较远的对象减小了尺寸。
正投影
有些图形软件包使用单位立方体作为规范化观察体,其x、y和z坐标规范在0到1之间。另外的规范化变换方法是使用坐标范围从-1到1的对称立方体。
由于屏幕坐标经常指定为左手系(参见下图),因此规范化观察体也常指定为左手系统。这样就可以将观察方向的正距离解释为离屏幕(观察平面)的距离。因此,可以将投影坐标转换为左手坐标系中的位置,并进一步由观察变换转换为左手屏幕坐标。

透视投影
当透视投影观察体是一个对称棱台时,透视变换将棱台内部的位置映射到矩形平行管道中的正交投影坐标。由于棱台中心线已经和观察平面垂直(参见下图),故平行管道的中心线就是棱台的中心线。这是棱台中所有投影线上的位置映射到观察平面上同一点 ( x p , y p ) (x_p,y_p) (xp,yp) 的结果。因此,每一投影线由透视变换转换成正交观察平面的线条时,因而平行于棱台的中心线。
使用转换到正交投影观察体后的对称棱台,可以进入下一步的规范化化变换。


透视投影将棱台观察体中的所有点变换成矩形平行管道观察体中的位置。透视变换过程的最后一步是将该平行管道映射到规范化观察体(normalized view volume)中。

规范化透视投影变换分两步进行:
- 将棱台观察体中的所有点变换成矩形平行管道观察体中的位置;
- 将该平行管道映射到规范化观察体中。
变换方法或规则
设有一点P,位于观察体内,其坐标为 ( x , y , z ) (x,y,z) (x,y,z),分别对x、y坐标和z坐标变换到 [ − 1 , 1 ] [-1, 1] [−1,1] 内的方式进行讨论:
- x、y坐标的变换方式:
1、视点(投影中心或投影参考点)与P点的连线与近裁剪面(即裁剪窗口)交于P’点;
2、设近裁剪面的宽度为W,高度为H,P’点的x坐标范围是 [ − W 2 , W 2 ] [-\frac{W}{2},\frac{W}{2}] [−2W,2W],y坐标范围是 [ − H 2 , H 2 ] [-\frac{H}{2},\frac{H}{2}] [−2H,2H],然后分别映射至 [ − 1 , 1 ] [-1, 1] [−1,1] 内。
- z坐标的变换方式
z坐标的范围是 z N e a r zNear zNear 至 z F a r zFar zFar,需要映射到 [ − 1 , 1 ] [-1, 1] [−1,1],映射方法待定。
变换步骤
在获得世界中某一点 p ( x w , y w , z w ) p(x_w, y_w,z_w) p(xw,yw,zw) 在视点坐标系下的坐标 p ( x v , y v , z v ) p(x_v, y_v,z_v) p(xv,yv,zv) 后,将其坐标进行规范化投影变换,即使得位于视锥体内的点的坐标 x , y , z ∈ [ − 1 , 1 ] x, y, z\in [-1, 1] x,y,z∈[−1,1]
1. 将棱台观察体中的所有点变换成矩形平行管道观察体中的位置
先计算出它在 近裁剪平面 上的投影坐标的 x v ′ , y v ′ x_v', y_v' xv′,yv′ 值
- 对y方向
y v ′ − z N e a r = y v z v y v ′ = − y v ⋅ z N e a r z v \frac{y_v'}{- zNear}=\frac{y_v}{z_v}\\ y_v'=-\frac{y_v\cdot zNear}{z_v} −zNearyv′=zvyvyv′=−zvyv⋅zNear - 对x方向
x v ′ − z N e a r = x v z v x v ′ = − x v ⋅ z N e a r z v \frac{x_v'}{-zNear}=\frac{x_v}{z_v}\\ x_v'=-\frac{x_v\cdot zNear}{z_v} −zNearxv′=zvxvxv′=−zvxv⋅zNear - 对z方向
z的坐标不变
z ′ = z z' =z z′=z
2. 将该平行管道映射到规范化观察体中
有近裁剪平面到投影中心或投影参考点的距离 zNear 和垂直方向上的视场角 fovy ,故可求得裁剪窗口的宽 W W W 和高 H H H:
H 2 = z N e a r ⋅ tan ( f o v y 2 ) \frac{H}{2}=zNear\cdot \tan(\frac{fovy}{2}) 2H=zNear⋅tan(2fovy)
∵ a s p e c t = W H ( 视 口 的 宽 高 之 比 ) \because aspect=\frac{W}{H} (视口的宽高之比) ∵aspect=HW(视口的宽高之比)
∴ W = H ⋅ a s p e c t \therefore W=H\cdot aspect ∴W=H⋅aspect
W 2 = a s p e c t ⋅ z N e a r ⋅ tan ( f o v y 2 ) \frac{W}{2}=aspect\cdot zNear\cdot \tan(\frac{fovy}{2}) 2W=aspect⋅zNear⋅tan(2fovy)
再由 近裁剪平面 上的投影坐标的 x v ′ , y v ′ x_v', y_v' xv′,yv′ 值求出其规范化坐标的 x v ′ ′ , y v ′ ′ x_v'', y_v'' xv′′,yv′′ 值:
y v ′ ′ = y v ′ H 2 y v ′ ′ = y v ′ z N e a r ⋅ tan ( f o v y 2 ) y v ′ ′ = − y v z v ⋅ tan ( f o v y 2 ) y_v''=\frac{y_v'}{\frac{H}{2}}\\ y_v''=\frac{y_v'}{zNear\cdot \tan(\frac{fovy}{2})}\\ y_v''=-\frac{y_v}{z_v\cdot \tan(\frac{fovy}{2})}\\ yv′′=2Hyv′yv′′=zNear⋅tan(2fovy)yv′yv′′=−zv⋅tan(2fovy)yv
x v ′ ′ = x v ′ W 2 x v ′ ′ = x v ′ a s p e c t ⋅ z N e a r ⋅ tan ( f o v y 2 ) x v ′ ′ = − x v z v ⋅ a s p e c t ⋅ tan ( f o v y 2 ) x_v''=\frac{x_v'}{\frac{W}{2}}\\ x_v''=\frac{x_v'}{aspect\cdot zNear\cdot \tan(\frac{fovy}{2})}\\ x_v''=-\frac{x_v}{z_v\cdot aspect\cdot \tan(\frac{fovy}{2})} xv′′=2Wxv′xv′′=aspect⋅zNear⋅tan(2fovy)xv′xv′′=−zv⋅aspect⋅tan(2fovy)xv
此处暂未确定其规范化坐标的 z ′ ′ z'' z′′ 的值。
此时写出 p p p 点的规范化投影坐标,如下 :
p ′ ′ ( − x v z v ⋅ a s p e c t ⋅ tan ( f o v y 2 ) , − y v z v ⋅ tan ( f o v y 2 ) , z v ′ ′ ) p''(-\frac{x_v}{z_v\cdot aspect\cdot \tan(\frac{fovy}{2})},-\frac{y_v}{z_v\cdot \tan(\frac{fovy}{2})},z_v'') p′′(−zv⋅aspect⋅tan(2fovy)xv,−zv⋅tan(2fovy)yv,zv′′)
p ′ ′ p'' p′′ 的齐次坐标:
p ′ ′ ( − x v z v ⋅ a s p e c t ⋅ tan ( f o v y 2 ) , − y v z v ⋅ tan ( f o v y 2 ) , z v ′ ′ , 1 ) p''(-\frac{x_v}{z_v\cdot aspect\cdot \tan(\frac{fovy}{2})},-\frac{y_v}{z_v\cdot \tan(\frac{fovy}{2})},z_v'',1) p′′(−zv⋅aspect⋅tan(2fovy)xv,−zv⋅tan(2fovy)yv,zv′′,1)
对 p ′ ′ p'' p′′ 的齐次坐标中的每一位都乘以 − z v -z_v −zv:
p ′ ′ ( x v a s p e c t ⋅ tan ( f o v y 2 ) , y v tan ( f o v y 2 ) , − z v ′ ′ ⋅ z v , − z v ) p''(\frac{x_v}{aspect\cdot \tan(\frac{fovy}{2})},\frac{y_v}{\tan(\frac{fovy}{2})},-z_v''\cdot z_v,-z_v) p′′(aspect⋅tan(2fovy)xv,tan(2fovy)yv,−zv′′⋅zv,−zv)
由此可以确定透视投影矩阵的部分内容:
( 1 a s p e c t ⋅ tan ( f o v y 2 ) 0 0 0 0 1 tan ( f o v y 2 ) 0 0 0 0 a b 0 0 − 1 0 ) ⋅ ( x v y v z v 1 ) \begin{pmatrix} \frac{1}{aspect\cdot\tan(\frac{fovy}{2})} & 0 &0&0\\ 0&\frac{1}{\tan(\frac{fovy}{2})}&0&0\\ 0&0&a&b\\ 0&0&-1&0\\ \end{pmatrix}\cdot\begin{pmatrix} x_v\\ y_v\\ z_v\\ 1 \end{pmatrix} ⎝⎜⎜⎜⎛aspect⋅tan(2fovy)10000tan(2fovy)10000a−100b0⎠⎟⎟⎟⎞⋅⎝⎜⎜⎛xvyvzv1⎠⎟⎟⎞
其中 a a a、 b b b 的值待定。
a ⋅ z v + b = − z v ′ ′ ⋅ z v a\cdot z_v+b=-z_v''\cdot z_v\\ a⋅zv+b=−zv′′⋅zv
同除 z v z_v zv
⇒ − a − b z v = z v ′ ′ \Rightarrow -a-\frac{b}{z_v}=z_v'' ⇒−a−zvb=zv′′
当 z v = − z N e a r z_v=-zNear zv=−zNear 时, z v ′ ′ = − 1 ⇒ − a − b − z N e a r = − 1 z_v''=-1\Rightarrow -a-\frac{b}{-zNear}=-1 zv′′=−1⇒−a−−zNearb=−1
当 z v = − z F a r z_v=-zFar zv=−zFar 时, z v ′ ′ = 1 ⇒ − a − b − z F a r = 1 z_v''=1\Rightarrow -a-\frac{b}{-zFar}=1 zv′′=1⇒−a−−zFarb=1
解出
a = z N e a r + z F a r z N e a r − z F a r a=\frac{zNear+zFar}{zNear-zFar}\\ a=zNear−zFarzNear+zFar
b = 2 ⋅ z N e a r ⋅ z F a r z N e a r − z F a r b=\frac{2\cdot zNear\cdot zFar}{zNear-zFar}\\ b=zNear−zFar2⋅zNear⋅zFar
故
M p e r s = ( 1 a s p e c t ⋅ tan ( f o v y 2 ) 0 0 0 0 1 tan ( f o v y 2 ) 0 0 0 0 z N e a r + z F a r z N e a r − z F a r 2 ⋅ z N e a r ⋅ z F a r z N e a r − z F a r 0 0 − 1 0 ) M_{pers}=\begin{pmatrix} \frac{1}{aspect\cdot\tan(\frac{fovy}{2})} & 0 &0&0\\ 0&\frac{1}{\tan(\frac{fovy}{2})}&0&0\\ 0&0&\frac{zNear+zFar}{zNear-zFar}&\frac{2\cdot zNear\cdot zFar}{zNear-zFar}\\ 0&0&-1&0\\ \end{pmatrix} Mpers=⎝⎜⎜⎜⎛aspect⋅tan(2fovy)10000tan(2fovy)10000zNear−zFarzNear+zFar−100zNear−zFar2⋅zNear⋅zFar0⎠⎟⎟⎟⎞
代码实现
OpenGL中的矩阵是以列为主标记次序。
如果以行主序存储该矩阵,在内存中的布局如下图所示:
如果以列主序存储该矩阵,在内存中的布局如下图所示:
行主序与列主序只是矩阵不同的存储形式,由它们表示的矩阵在数学意义上是全等的,这对矩阵的算法和矩阵的操作结果是没有影响的。
mat4x4 perspective(
float const & fovy,
float const & aspect,
float const & zNear,
float const & zFar
)
{
const float tanHalfFOV = tanf(ToRadian(fovy / 2.0f));
mat4x4 Result;
Result[0][0] = 1.0f / (tanHalfFOV * aspect);
Result[1][1] = 1.0f / tanHalfFOV;
Result[2][2] = - (zNear + zFar) / (zFar - zNear);
Result[2][3] = - 1.0f;
Result[3][2] = - (2.0f * zFar * zNear) / (zFar - zNear);
return Result;
}
延申:
- 将棱台观察体中的所有点变换成矩形平行管道观察体中的位置,有矩阵 M p e r s → o r t h o M_{pers\rightarrow ortho} Mpers→ortho
- 将该平行管道映射到规范化观察体中(与平行投影的规范化变换相同),则有矩阵 M o r t h o , n o r m M_{ortho,norm} Mortho,norm
此时有
M p e r s , n o r m = M o r t h o , n o r m ⋅ M p e r s → o r t h o M_{pers,norm}=M_{ortho,norm}\cdot M_{pers\rightarrow ortho} Mpers,norm=Mortho,norm⋅Mpers→ortho
参考资料
- 透视投影矩阵的推导
- 《计算机图形学(第四版)》电子工业出版社出版