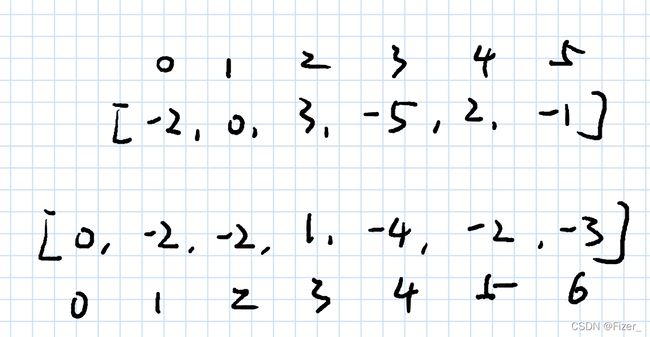LeetCode（持续更新）
2021.12.6
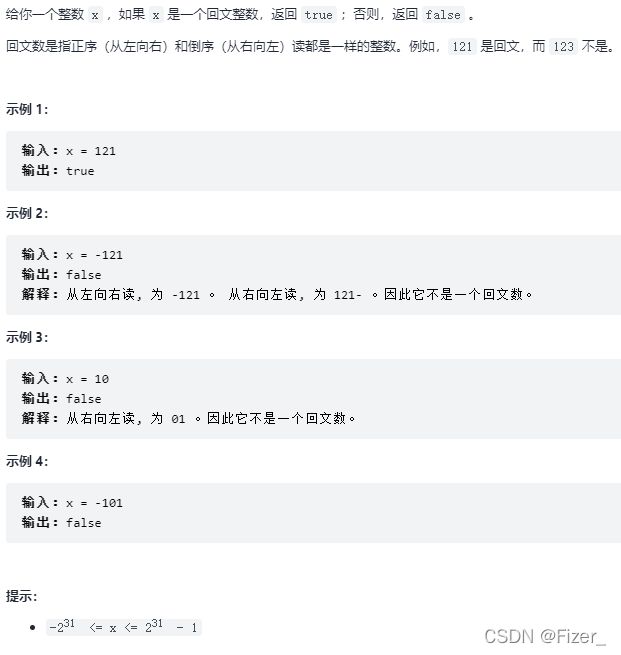
7.整数反转
本题的困难在于判断反转后的数据是否超出范围
我的代码如下：
class Solution {
public int reverse(int x) {
int num=0;
if(x>-10&&x<10){
return x;
}
while(x<=-10||x>=10){
num=num*10+x%10*10;
x/=10;
if(num<-2147483648||num>2147483647)
return 0;
}
num+=x;
if(num<-2147483648||num>2147483647){
return 0;
}
else return num;
}
}但是我还是出错了，问题在于使用int的时候如果超出范围它会自动丢失数据而不是报错，我在idea上得到的结果如下：
public class example {
public static void main(String[] args) {
int i=1534236469;
int num=0;
while(i<-10||i>10){
num=num*10+i%10*10;
i/=10;
System.out.print(num+" ");
System.out.println(i);
}
num+=i;
}
}
结果如下：
90 153423646
960 15342364
9640 1534236
96460 153423
964630 15342
9646320 1534
96463240 153
964632430 15
1056389758 1最后看了一眼答案，发现其实关键的代码还是差不多，主要是判断方法改进了很多，主要体现在对临界值的判断上，代码如下：
class Solution {
public int reverse(int x) {
int res = 0;
while(x!=0) {
//每次取末尾数字
int tmp = x%10;
//判断是否 大于 最大32位整数
if (res>214748364 || (res==214748364 && tmp>7)) {
return 0;
}
//判断是否 小于 最小32位整数
if (res<-214748364 || (res==-214748364 && tmp<-8)) {
return 0;
}
res = res*10 + tmp;
x /= 10;
}
return res;
}
}
对于大于零的数，若最后的结果的个位数大于7且前面为214748364，则判断为溢出，复数同理。
自己在细节上还是有很多没有考虑到的地方，一心只想着暴力解答，以后还是得多注意。
9.回文数
这题看完它给的例子可以很快得出结论：负数一定不是回文数，所以只需要判断正数即可
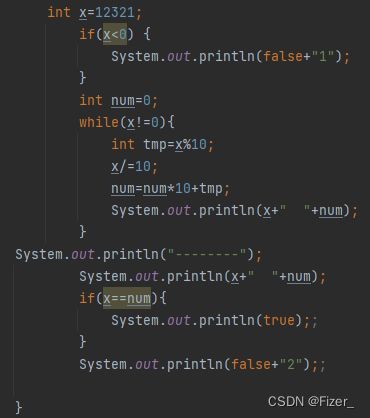
我第一次写的代码报错了，如下：
class Solution {
public boolean isPalindrome(int x) {
if(x<0) {
return false; //负数直接返回false
}
int num=0;
while(x!=0){
int tmp=x%10; //得到x的个位数字
x/=10;
num=num*10+tmp;
}
if(x==num){
return true;
}
return false;
}
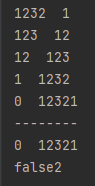
}但是报错了，我看了一会儿没找到什么逻辑上的错误，于是打开idea查看。
在每一步进行值的输入，结果显而易见 （如右图所示），while中的逻辑是没有什么问题的，关键在于使用while之后x的值也会改变（x=0），所以给出解决方案：用int类型的变量y在while之前接收x，再用y与num比较即可。代码如下：
class Solution {
public boolean isPalindrome(int x) {
int y=x; //用y接收x的值
if(x<0) {
return false;
}
int num=0;
while(x!=0){
int tmp=x%10;
x/=10;
num=num*10+tmp;
}
if(y==num){ //用y与num比较，此时x=0
return true;
}
return false;
}
}反思：这道题比（7.整数反转）要简单，因为不用判断负数也不用判断int的取值范围，关键代码部分其实很相近，都是取余和取模的应用。同时还复习到了内部变量和外部变量的变化对结果的影响，在之后的学习过程中还是不能想当然的写代码。
12.25
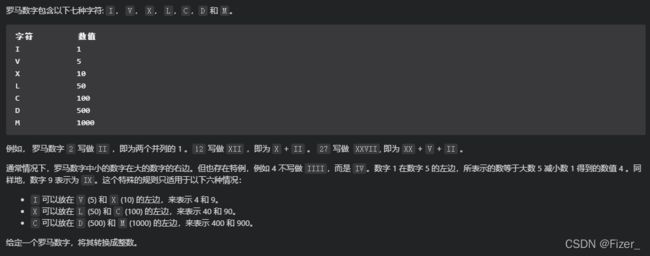
13.罗马数字转整数
上一周考试，所以这周补上一周的题目。
说实话，第一眼看过去没什么思路，但也发现了一些规律，即当小的数字在大的数字左边时，表示为减，且这种情况只发生在“4”和“9”上。然后看了一下高赞解答。
发现他并没有局限于 “4”和“9”上，这点对我来说很关键，因为我最开始的想法是将特殊的六种情况单独列出来，再用一种方法将剩下的情况表达出来。但是表示 “4”和“9”的实际上也有n种，故无法实现。
在快速浏览了一遍博主的代码之后尝试自己写。
第一次的代码如下：
class Solution {
public int romanToInt(String s) {
int pre=getnum(s.charAt(0));
int sum=0;
for (int i=1;i结果调试的时候不对，于是在纸上再演算一下过程，发现原因是当num为s的最后一个字符，且判断完成后，执行 pre=num，此时pre并没有加到sum里面，故在for循环之后需要再加一个sum+=pre。
最终代码如下：
class Solution {
public int romanToInt(String s) {
int pre=getnum(s.charAt(0));
int sum=0;
for (int i=1;i完成。
反思：这个题目的整体思路其实不难，我一开始没有做出来的原因还是被题目给的提示信息给骗了，今后做题的时候还是得看到题目的最本质想法。
2022.2.24
14.最长公共前缀
时隔两个月（放寒假），重新开始写题，多少有些生疏了，导致这道题卡了很久，总是不知道怎么解决这个bug，接下来放上我的做题过程。
题目如下
这道题逻辑上很简单，就是找出相同前缀然后比较。我的第一想法是先比较第一个和第二个的最大前缀，用m表示这两个的最大前缀个数，同时将其赋值给ans。接下来就是用ans依次和剩下的字符串数组比较，并且不断更新m和ans。
ok，理论存在，开始实践。我的第一次代码如下：
class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs.length==0) return "";
String s1=strs[0]; //取数组中的第一个字符串，赋给s1
if(strs.length==1) return s1;
String s2=strs[1]; //取数组中的第二个字符串，赋给s2
int m=0;
for(int i=0;i执行代码没报错，但是提交以后出现了错误：
这题最后的输出应该是“c”，但是我的代码输出的是“cr”。将代码复制到idea中发现了原因：在从第一个和第二个中找ans时就出现了错误，按道理cir和car到了第二个，即i和a时就该停止找ans，但是这里继续在后面的字母中找相同的，所以也很好改，即在第一个for循环中之后加一个停止就行：
for(int i=0;i信心满满继续执行，发现还是报错，并且是只剩最后一个bug：
出错的原因是：输入的一串a中有一个“aab”，想了一会儿发现第二段代码中并没有更新ans的代码，于是补上，如下：
for (int j=2;j最后执行没问题，最终代码如下：
class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs.length==0) return "";
String s1=strs[0]; //取数组中的第一个字符串，赋给s1
if(strs.length==1) return s1;
String s2=strs[1]; //取数组中的第二个字符串，赋给s2
int m=0;
for(int i=0;i反思：这道题的逻辑非常简单，花了很长时间的原因还是因为两个细节没有注意到。同时此代码的内存占用较大，达到了39.1M。不过此阶段还是以能做出来为主，之后再学会优化代码。
2022.2.27
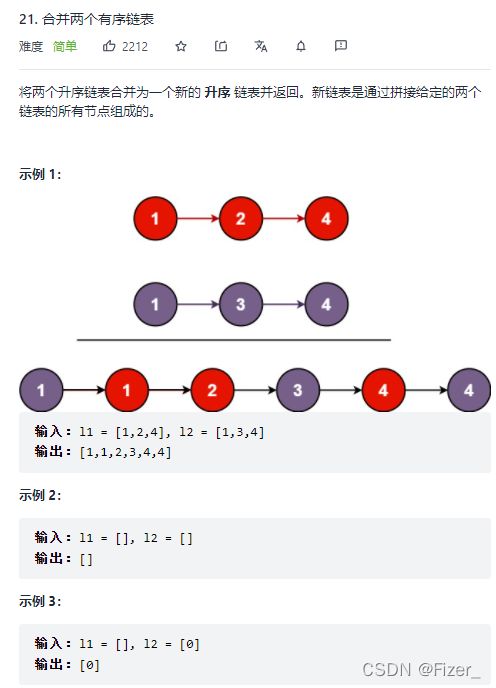
21.合并两个有序链表
题目如下：
这道题的思路就是用两个指针p1和p2在两个链表之间不断比大小然后插入到新的一个链表即可，但是我还是第一次写链表的题目，代码上出了很多小bug，修改了很多次。
最终代码如下：
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode ans=new ListNode();
ListNode p0=ans;
ListNode p1=list1;
ListNode p2=list2;
while(p1!=null&&p2!=null){
if(p1.val这里需要注意的是最后return的是ans.next而不是直接return ans，因为在创建的时候，头指针默认为0，所以返回的时候得从第二个开始。
2022.3.13
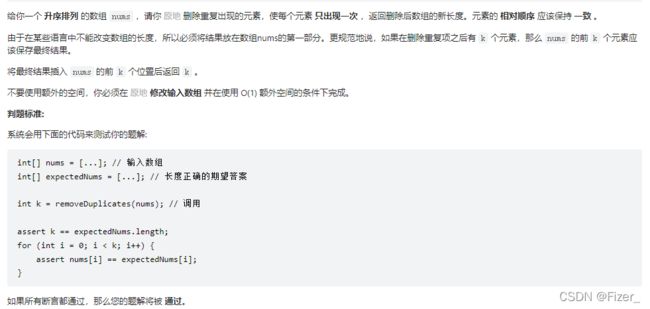
26. 删除有序数组中的重复项
题目如下：
第一遍读题的时候其实卡了很久，因为Java中的数组好像并没有直接删除的功能，往常做的数组题目也都是用的另外一个数组接收。再多看了几遍题目之后发现这道题只是需要将不重复的元素放到数组左边即可。故思路应该比较明确，肯定是用两个index进行循环操作，其中一个用来标记不重复的元素，另一个用来标记重复的元素，代码如下：
class Solution {
public int removeDuplicates(int[] nums) {
int i=0,j=1;
//i用来标记非重复元素，j用来标记重复元素
if(nums.length==1) return 1;
while(j!=nums.length){
if(nums[i]==nums[j]){
j++; //找到最后一个和i相同的元素
}else{
nums[i+1]=nums[j];//然后将i后面的元素即重复的第二个元素换成不重复元素
i++;
j++;
}
}
return i+1;
}
}2022.3.15
27.移除元素
题目如下：
看到题目就想起了上一次做的题目（26题），这两题都是数组，都是双指针，所以思路上也差不太多。代码如下：
class Solution {
public int removeElement(int[] nums, int val) {
int j=0;
for(int i=0;i用i指针遍历数组，遇到不等于val的数就放到前面。
我最开始的思路是找到val然后放后面，操作起来会麻烦很多。有时候换位思考真的很重要。
2022.3.17
28. 实现 strStr()
题目如下
这题思想不难啊，我觉得类似于滑动窗口吧，就是用短的不断在长的里面比较。但是从开始到成功执行还是花了很长时间。先附上代码：
class Solution {
public int strStr(String haystack, String needle) {
int num1=haystack.length();
int num2=needle.length();
if(num1=num2) {return i;} （2）
}
}
return -1;
}
} 当时代码一直报错，都是数组越界的异常，但是指的地方不对所以找半天。最后在（1）（2）两个地方加了两个等号就可以运行了。
总结原因还是因为数组的开始和长度的开始不一样，一个是0一个是1。
研一下学期开始组会两周开一次，因此题目也将以每两周一个分块为单位进行更新。
2022.3.28-2022.4.10
1.303. 区域和检索 - 数组不可变 （数组前缀和）
这道题目的描述如下：
这道题是labuladong的算法小抄的第一题。在解题思路上不难，我最开始的想法就是暴力穷举 ，用right-left得到所需要计算的数字个数，然后进行一个for循环得到区域和。这个题目所引出的思想是数组的前缀和，即用一个新的数组，其长度是原数组长度+1，用来存储前一个数组对应的前n项和，然后直接用[right]-[left]即可达到答案。（如图所示）
最后附上代码
class NumArray {
private int [] prenums;
public NumArray(int[] nums) {
prenums=new int[nums.length+1];
prenums[0]=0; //第一位一定是0.
for(int i=1;i2. 66. 加一
这道题目描述如下：
首先解题思路很明显，分两种情况：
1.尾数不为9，直接加1返回。
2.位数为9，则需要考虑进位问题和数组长度问题。这道题主要就是要解决位数为9的情况。
附上代码：
class Solution {
public int[] plusOne(int[] digits) {
if(digits[digits.length-1]==9){ //位数为9
int i=digits.length-1;
while(digits[i]==9&&i>=0){ //考虑进位
digits[i]=0;
if(i==0){ //当超出原数组范围，创建一个新数组
int [] digits2=new int [digits.length+1];
digits2[0]=1; //由于新数组默认值全为0，故令第一位为1即可
return digits2;
}
i--;
}
digits[i]+=1;
return digits;
}
digits[digits.length-1]+=1; //位数不为9，直接加1返回
return digits;
}
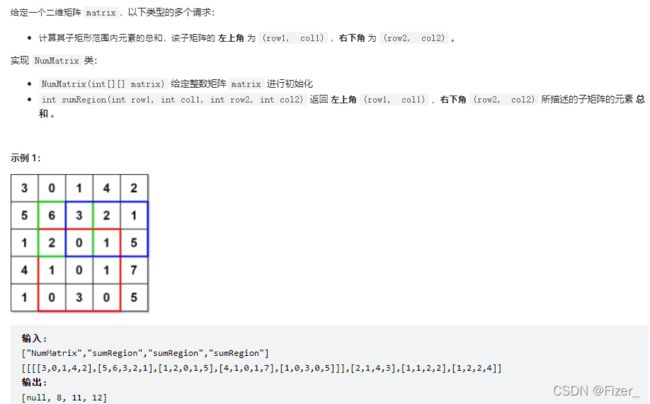
}3.304. 二维区域和检索 - 矩阵不可变
这道题目是一维数组前缀和的升级版本，即在二维数组的前提下使用前缀和进行答题。
题目如下：
这道题整体思路还是不难，暴力算法也很简单，如下：
class NumMatrix {
private int [][]matrix;
public NumMatrix(int[][] matrix) {
this.matrix=matrix;
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum=0;
for(int i=row1;i<=row2;i++){
for(int j=col1;j<=col2;j++){
sum+=matrix[i][j];
}
}
return sum;
}
}当然用前缀和的方式将大大增加计算机的效率但是在代码方面我认为是比暴力算法略复杂的，仅供参考：
class NumMatrix {
int[][] res;
public NumMatrix(int[][] matrix) {
res=new int[matrix.length+1][matrix[0].length+1];
for(int i=0;i4.560. 和为 K 的子数组
这道题也是前缀和类型的很好应用。题目描述如下：
我认为这道题在没学前缀和之前也能做，只是学了前缀和之后将更简单，将它视为一个中等难度的题目我觉得有点勉强了，附上代码：
class Solution {
public int subarraySum(int[] nums, int k) {
int []pre=new int [nums.length+1];
int res=0;
pre[0]=0;
for(int i=1;i整体思路上跟前两个前缀和并无多大差别，最优算法是利用前缀和与哈希表相结合的方法，说实话没太看懂...
import java.util.HashMap;
import java.util.Map;
public class Solution {
public int subarraySum(int[] nums, int k) {
// key：前缀和，value：key 对应的前缀和的个数
Map preSumFreq = new HashMap<>();
// 对于下标为 0 的元素，前缀和为 0，个数为 1
preSumFreq.put(0, 1);
int preSum = 0;
int count = 0;
for (int num : nums) {
preSum += num;
// 先获得前缀和为 preSum - k 的个数，加到计数变量里
if (preSumFreq.containsKey(preSum - k)) {
count += preSumFreq.get(preSum - k);
}
// 然后维护 preSumFreq 的定义
preSumFreq.put(preSum, preSumFreq.getOrDefault(preSum, 0) + 1);
}
return count;
}
}
5.1248. 统计「优美子数组」
这道题依旧是前缀和的题目，由于上一道题没看懂，在看题解的时候有博主建议先做做第1、1248、和454道题，所以我先把第1248题做了做，题目如下：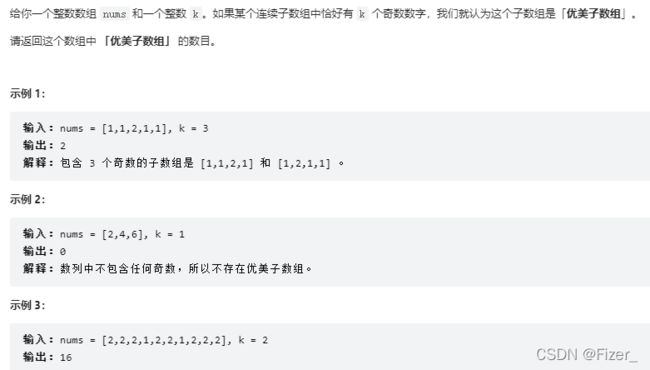
现在看到这种数组问题我首先就会想到是不是会用前缀和的算法，其实我的第一反映是用另一个数组记录前缀奇数的个数，笔记如下： 
即用前缀和的思想存储前缀奇数，然后再用两个for循环进行判断，但是超时了，附上代码：
class Solution {
public int numberOfSubarrays(int[] nums, int k) {
int []prenum=new int [nums.length+1];
prenum[0]=0;
int acount=0;
int res=0;
for(int i=1;i其实代码还算简洁但是时间复杂度已经是n平方了，然后考虑hashmap的方法进行改写。其实整体思路还是不变，创建一个原数组长度+1的新数组prenum[]用来记录，[]内为子数组中奇数的个数，值为子数组的个数。附上代码：
class Solution {
public int numberOfSubarrays(int[] nums, int k) {
int []prenum=new int [nums.length+1];
int acount=0;
prenum[acount]=1;
int res=0;
for(int i=1;i=k){
res+=prenum[acount-k];
}
}
return res;
}
} for循环里面第一个if是判断是否为奇数，如果不是就直接+1，若是则account先++再+1。第二个if用来判断，当account>k的时候就肯定会有结果增加，这一步对应于暴力算法中嵌套的两个for循环中的内循环。
6.1109. 航班预订统计
这道题又是一个新的知识点，叫差分数组。整体思想上和前缀和很接近，都是先构造一个新的数组，不过差分数组是用来存放相邻两个数之间的差值。题目如下：
像这种取一段子数组进行加减操作的大概率为差分数组题目。除此之外还学到了一个新的知识点，就是对于二维数组nums，nums.length返回的是行数，nums[0].length返回的是列数。ok回到本题，题目给了起始位置，结束位置以及需要做的操作，那么就很简单了。首先先搞懂什么是差分数组（我个人觉得这个比前缀和要稍微难一点），定义就先不讲了，直接说说操作。对差分数组上的某个位置进行加减操作会得到什么？例如一个数组nums[1,2,3,4,5]，其差分数组diff为[1,1,1,1,1]，如果我对i=2的位置进行+5操作会得到[1,1,6,1,1]，那么将此数组还原看看会得到什么：那么问题又来了，怎样将差分数组还原？其实就是再加回去呗，定义一个ans数组，0位置和diff位置一样，然后i位置为ans[i]=ans[i-1]+diff[i]。得到ans[1,2,8,9,10]，是不是就是在i=2之后所有的位置都+5了。那么要想在某个范围内，如i-j的范围内进行操作，那么就先对i位置进行+操作，然后对j+1位置进行-操作即可，然后再还原即可得到答案。代码如下：
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int []ans=new int[n];
for(int i=0;i7.20. 有效的括号
这是一道很经典的栈问题，整体思路就是若上一个位置和此位置能形成一个完整的括号就出栈，否则进栈，当然还有一些小细节，比如当s的长度为0或为奇数时，直接返回false等。题目图下：
代码如下：
class Solution {
public boolean isValid(String s) {
char [] array=new char[s.length()];
if(s.length()==0||s.length()%2!=0) return false;
int top=0;
for(int i=0;i这里需要注意一点的就是for循环中右括号里的if语句，由于java对与或非语句进行了优化，所以在用且（&&）的时候，若前一个条件不成立则直接跳过第二个条件。因此得将top！=0放在前面，刚开始我放在后面导致代码报了超出数组长度的错，换了个位置就解决了。
7.69. x 的平方根
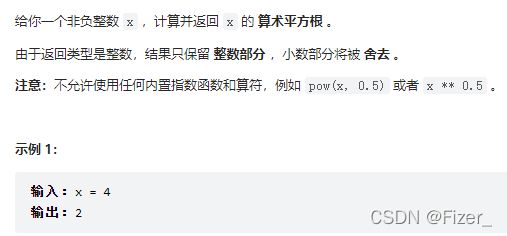
题目很简洁，就是用最原始的方法求非负整数的算术平方根。
这道题我的第一想法是不断用x/2来更新平方更a，然后用a*a和x比大小，更接近的就是答案，但是这想法错了，因为3的平方比2的平方更接近8，但是8开平方根去掉小数之后是2。因此想到了二分查找来判断，但是我自己在很多细节上有很多遗忘的地方，所以参考了题解答案，代码如下：
class Solution {
public int mySqrt(int x) {
int left=1;
int right=x/2;
if(x==0||x==1) return x;
while(leftx/mid) right=mid-1;
if(mid<=x/mid) left=mid;
}
return left;
}
} 这段代码有几个很细的点得单独拿出来说。首先mid的值是mid=left+(right-left+1)/2，为什么要+1（即向上取整）呢？这是因为当区间范围内只剩下left和right之后，会造成死循环，故需要向上取整而不是向下取整。然后就是if语句中的mid>x/mid，为什么不是mid*mid>x？因为乘法可能会让数据溢出，而除法就不会。（这也是我在看了解答之后才能理解到的，只能说很巧妙的化解了问题，优化代码这方面我还是比较欠缺。）
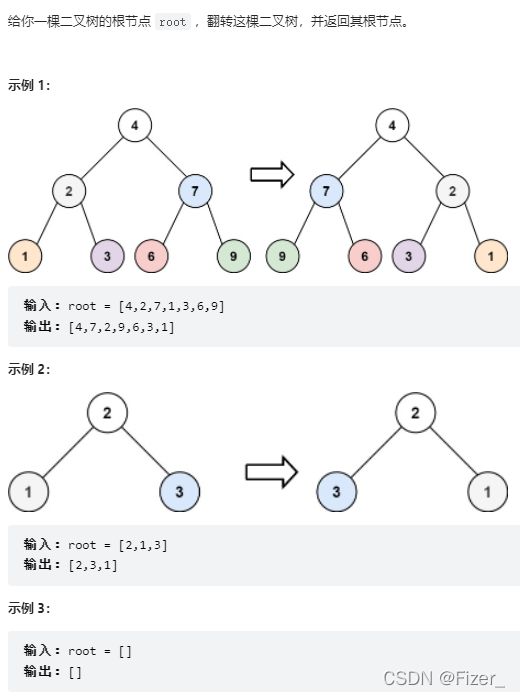
8.226. 翻转二叉树
这道题思想和代码都比较简单，直接用一个递归就行了，就是树的一些代码可能还需要记一记。
题目如下：
过程就是对根节点的左右子树交换一下位置即可，看这题的意思也没有说要判断是否是完全二叉树，所以直接交换即可，然后分别递归左子树和右子树。代码如下：
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root==null) return null;
TreeNode temp;
temp=root.left;
root.left=root.right;
root.right=temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}2022.4.11-2022.4.24
1.116. 填充每个节点的下一个右侧节点指针
这道题依然可以用递归的方法很快解决问题。到现在为止我对树还不是很了解，虽然之前学过数据结构但是在代码上还是有一些问题，我觉得还得多写几道树的题才好深刻理解。回到这题，如下：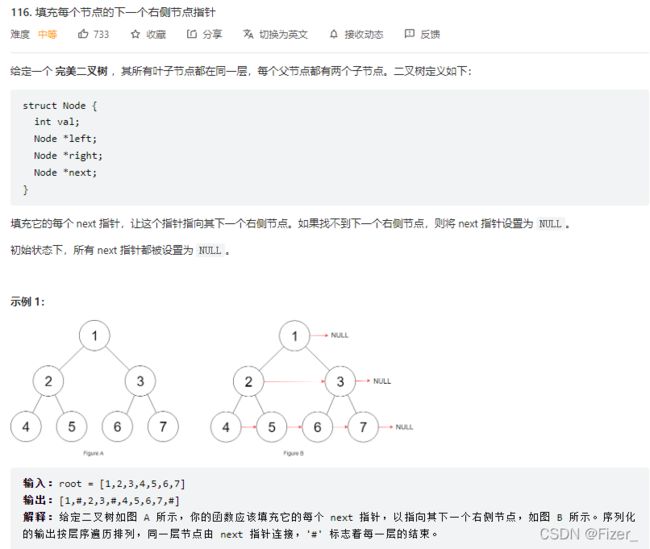
这道题目刚开始的时候我是不知道该怎么写的，就是感觉脑袋很空，不知道该怎么用代码实现，然后看了东哥的算法秘籍，用递归就很简单了，代码如下：
class Solution {
public Node connect(Node root) {
if(root==null||root.left==null){
return root;
}
nodes(root.left,root.right);
return root;
}
void nodes(Node n1,Node n2){
if(n1==null||n2==null) {
return ;
}
n1.next=n2;
nodes(n1.left,n1.right);
nodes(n1.right,n2.left);
nodes(n2.left,n2.right);
}
}不过还出现了一个小插曲，一开始的时候一直报error: '(' expected错，搞了半天不知道为什么，后来才发现是因为我在定义nodes函数的时候，用了void又用了Node...有时候这些小错误真的很让人抓狂！
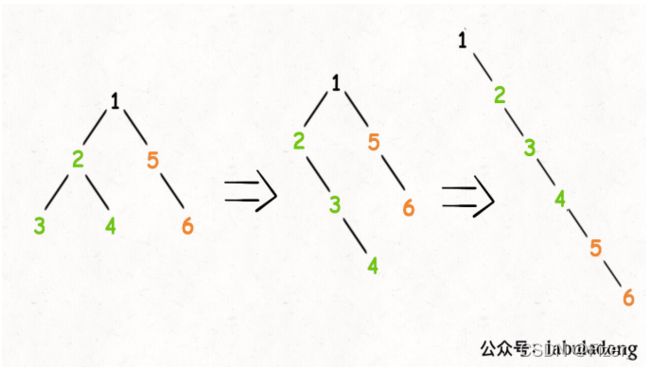
2.114. 二叉树展开为链表
这道题依旧是用的递归，依然没思路，直接上题目和代码
代码：
class Solution {
public void flatten(TreeNode root) {
if(root==null){return ;}
flatten(root.left);
flatten(root.right);
TreeNode left=root.left;
TreeNode right=root.right;
root.left=null;
root.right=left;
TreeNode p=root;
while(p.right!=null){
p=p.right;
}
p.right=right;
}
} 画图出来就是这个样子：
这样看起来就好理解多了，代码实现起来也不是很困难。
3.70. 爬楼梯
这道题蛮有意思的，其实就是斐波那契数列换了个皮肤而已，题目如图：
看到题目我第一反应就是用递归，即return climb（n-1）+climb（n-2）。因为最后一级台阶智能是1或2，因此就是将这两种情况加起来就可以了，然后加上base if(n==1) return 1;和 if(n==2) return 2; 但是很遗憾超时了，所以就想到用for循环来代替递归，最终代码如下：
class Solution {
public int climbStairs(int n) {
if(n==1) return 1;
if(n==2) return 2;
int n1=1;
int n2=2;
int sum=0;
for(int i=3;i<=n;i++){
sum=n1+n2;
n1=n2;
n2=sum;
}
return sum;
}
}
递归代码如下：
class Solution {
public int climbStairs(int n) {
if(n==1) return 1;
if(n==2) return 2;
return climbStairs(n-1)+climbStairs(n-2);
}写完这题之后还是得重新回顾一下斐波那契数列
4.83. 删除排序链表中的重复元素
这道题比较简单，当时学数据结构的时候经常做，所以不多说了。
class Solution {
public ListNode deleteDuplicates(ListNode head) {
if(head==null) return head;
ListNode p=head;
ListNode q=p.next;
while(q!=null){
if(p.val==q.val){
p.next=q.next;
q=p.next;
}else{
p.next=q;
p=q;
q=q.next;
}
}
return head;
}
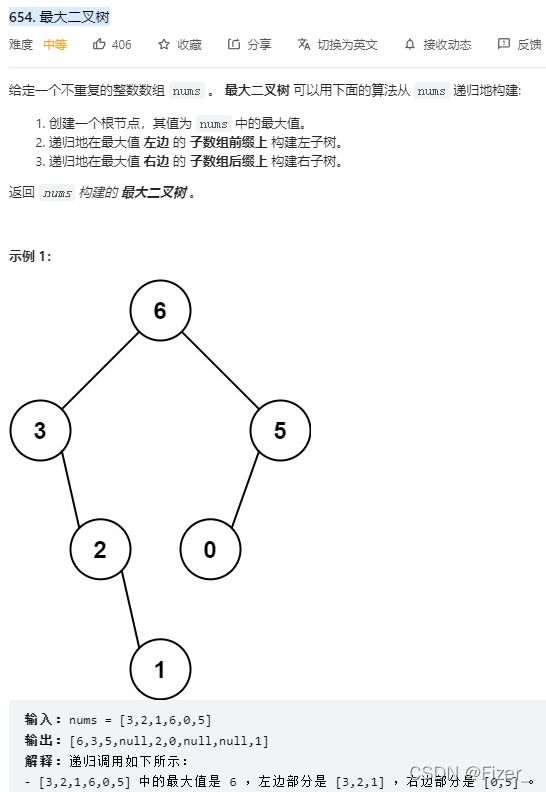
}5.654. 最大二叉树
这道题依旧是对递归的练习。上题目：
这道题和数据结构里面的某一个排序很像，但我忘记叫啥名字了，反正就是从中间到两边然后每次都在新的半边排序。所以一开始的思路就很明确了，就是用一个for循环不断找到小部分中的最大值，然后用max记录最大值，用mid记录位置 。这道题的难点对我来说就是如何将找到的最大值赋给树，然后什么时候递归。最后看了一下题解，附上代码：
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return dfs(nums,0,nums.length-1);
}
TreeNode dfs(int[] nums,int left,int right){
if(left>right) return null;
int max=-1;
int mid=-1;
for(int i=left;i<=right;i++){
if(nums[i]>max){
max=nums[i];
mid=i;
}
}
TreeNode root=new TreeNode(max);
root.left=dfs(nums,left,mid-1);
root.right=dfs(nums,mid+1,right);
return root;
}
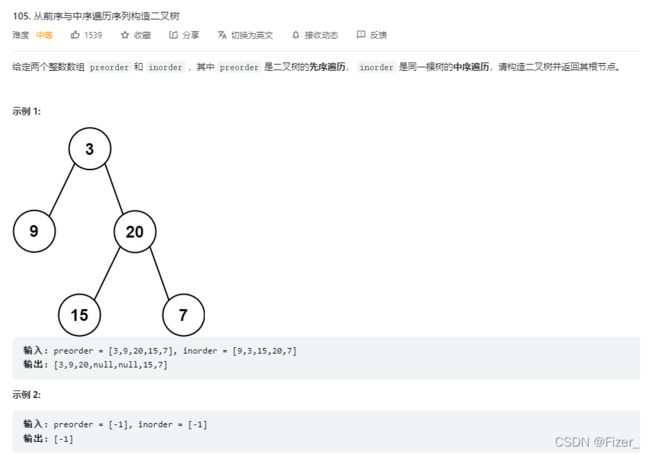
}6.105. 从前序与中序遍历序列构造二叉树
上题目：
说实话这道题目还是蛮难的，一开始一直绕的很，在边界的确定上搞了半天，先附上代码：
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return build(preorder,0,preorder.length,
inorder,0,inorder.length);
}
TreeNode build (int[] preorder,int pstar,int pend,
int[] inorder,int istar,int iend){
if(pstar>=pend) return null;
int roolval=preorder[pstar];
int index=0;
for(int i=istar;i解析上说Java通常是左闭右开的区间（其实是可以自定义的），这样理解来看确实是好解释了。其中left是用来确定左子树的位置，index是在inorder里面找到根节点。
7.106. 从中序与后序遍历序列构造二叉树
这道题和上一道题几乎完全一样，就是将前序和中序改成了后序和中序，即在确定left和index的时候有不一样，剩下的基本没什么改变，要注意的就是递归时的边界问题，这个问题昨天困扰了我一整天...上题目和代码
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return build(postorder,0,postorder.length-1,
inorder,0,inorder.length-1);
}
TreeNode build(int[] postorder,int pstar,int pend,
int[] inorder,int istar,int iend){
if(pstar>pend){return null;}
int index=0;
int rootval=postorder[pend];
for(int i=istar;i<=iend;i++){
if(inorder[i]==rootval){
index=i;
break;
}
}
TreeNode root=new TreeNode(rootval);
int left=iend-index;
root.left=build(postorder,pstar,pend-left-1,
inorder,istar,index-1);
root.right=build(postorder,pend-left,pend-1,
inorder,index+1,iend);
return root;
}
}这道题和上一道题真的应该多看几遍，很经典而且也需要很细心。这道题的边界上是左闭右闭，和上面不一样，因为postorder是最后一个结点为根节点所以得右闭。
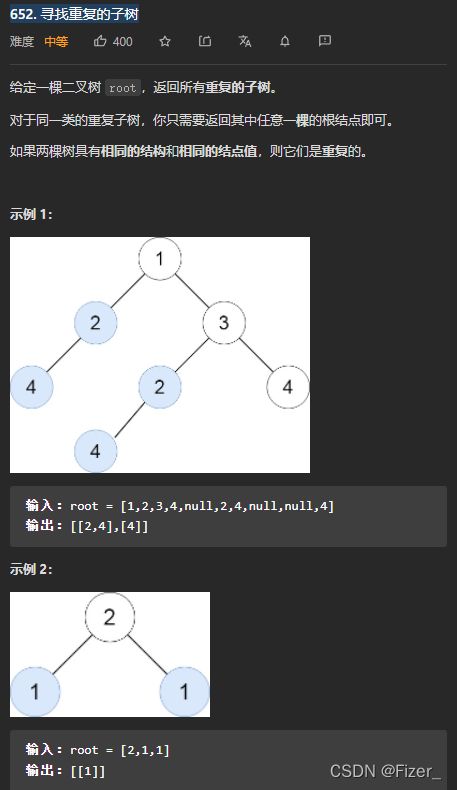
8.652. 寻找重复的子树
这道题目非常好，结合了后序遍历+二叉树序列化+hashmap，虽然我不会做，但是看完代码还是收获颇多的，上题目和代码：
class Solution {
HashMap num=new HashMap<>(); //记录子树出现次数
LinkedList res=new LinkedList<>(); //用来存储答案
public List findDuplicateSubtrees(TreeNode root) {
traverse(root); // 序列化
return res;
}
String traverse(TreeNode root){
if(root==null) return "#";
String left=traverse(root.left);
String right=traverse(root.right);
//后序遍历代码位置开始
String subtree=left+","+right+","+root.val; //生成该树的序列
int account=num.getOrDefault(subtree,0);
//判断subtree出现次数
if(account==1){
res.add(root);
}
num.put(subtree,account+1);
return subtree;
}
} 这道题复习了hashmap和linkedlist的相关用法以及后序遍历代码位置和序列化操作。值得多看几遍！
9.297. 二叉树的序列化与反序列化
这道题的难度是困难，同时序列化和反序列化对我来说也是一个新的知识点。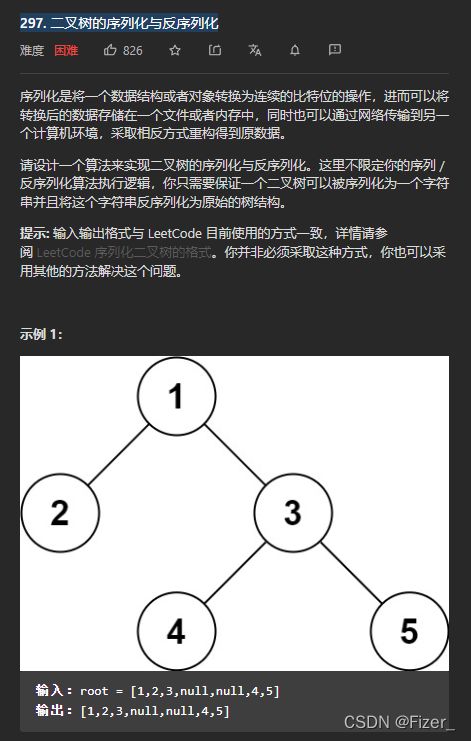
在上一题中，已经知道了序列化的相关思想和代码，故问题不是很多，主要问题集中在反序列化中，以及一些我没见过的方法。
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder builder = new StringBuilder();
return serialize(root,builder).toString();
}
StringBuilder serialize(TreeNode root,StringBuilder builder) {
if(root == null) {
builder.append("#").append(",");
return builder;
}
builder.append(root.val).append(",");
serialize(root.left,builder);
serialize(root.right,builder);
return builder;
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
LinkedList nodes = new LinkedList();
for(String node : data.split(",")) {
nodes.addLast(node);
}
return deserialize(nodes);
}
TreeNode deserialize(LinkedList nodes) {
if(nodes.isEmpty()) {
return null;
}
//移除列表中的父节点
String item = nodes.removeFirst();
if("#".equals(item)) {
return null;
}
//构建父节点
TreeNode root = new TreeNode(Integer.parseInt(item));
//序列化其左右子节点
root.left = deserialize(nodes);
root.right = deserialize(nodes);
return root;
}
} 在序列化时这里用了StringBuilder来高效拼接字符串，在反序列化的时候用LinkedList列表来存储得到的字符串，这里用到了列表的removeFirst方法和addLast方法。
addLast方法的作用是在链表的最后加上node，与之相对应的就是addFirst，就是在链表的开头加上node。
removeFirst方法的作用是先判断头节点是否为空，若不为空则返回该节点并指向该节点的next节点。
2022.4.25-2022.5.8
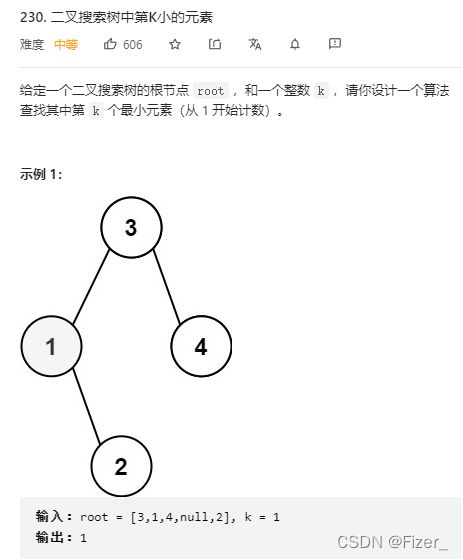
1.230. 二叉搜索树中第K小的元素
这道题抓住关键，即二叉搜索树的中序遍历是从小到大排序即可。我这道题是用一个数组记录排序后的顺序，然后返回第k个值。代码如下：
class Solution {
int [] nums=new int[10001];
int i=1;
public int kthSmallest(TreeNode root, int k) {
bst(root);
return nums[k];
}
void bst(TreeNode root){
if(root==null) return ;
if(root.left==null){
nums[i++]=root.val;
}
bst(root.left);
if(root.left!=null){
nums[i++]=root.val;
}
bst(root.right);
}
}2.538. 把二叉搜索树转换为累加树
这道题和上一题类型一样，都是中序遍历的题目，但是这道题目在设计上会更有趣一些。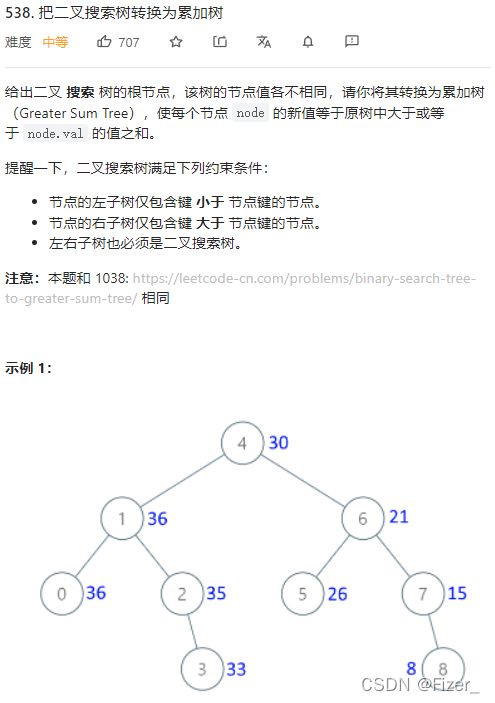
可以很明显的看出来，这道题目的意思就是，在得到中序遍历后得到的序列之后，然后再对得到的序列进行一个后缀和再赋值给根节点就行。我一开始是这样的想法但是实现起来比较麻烦，我还是被困在了使用数组的全套中。其实这题可以很简单，直接用一个递归，再中序遍历的位置上求和再赋值即可。不过需要注意的是，这里的递归顺序是先右子树再左子树，而一般的遍历是先左再右。
class Solution {
public TreeNode convertBST(TreeNode root) {
traverse(root);
return root;
}
int sum=0;
void traverse(TreeNode root){
if(root==null) return ;
traverse(root.right);
sum+=root.val; //得到逆序的值
root.val=sum; //将该值赋给根节点
traverse(root.left);
}
}这道题的代码很简洁但是我还是想了写了一个小时然后错了。我的思路还是不明晰，多做。
3.450. 删除二叉搜索树中的节点
还是二叉搜索树的题目，印象里这道题当时学数据结构的时候做过，思路就是在左子树中找到最大值或在右子树中找到最小值然后不断下沉，最后删除即可。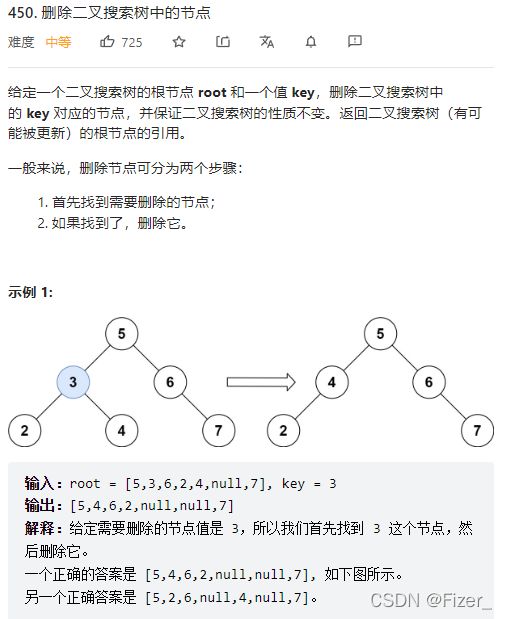
所以这道题在想法上没有多难，直接就写了，但是我还是写了很久，主要还是之前学的知识有点忘记了。附上代码
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root==null) return null;
if(root.val==key){
if(root.left == null&&root.right == null){
return null;
} // 第一种情况，即本身就是根节点，直接返回null
else if (root.left == null) return root.right; //如果左子树为空，则向右遍历
else if (root.right == null) return root.left; //如果右子树为空，则向左遍历
TreeNode p=new TreeNode(); //都不满足，即最复杂情况
p=root.left; //在左子树中找到最大的接替自己
while(p.right!=null){
p=p.right;
}
root.val=p.val; //将找到的左子树中的最大值赋给该节点，完成删除操作
root.left = deleteNode(root.left, p.val); //（这句话我没想到）完成赋值操作后，再在左子树上完成“下沉”操作
return root; //最后变成根节点后删除（变成情况1）
}
else if(root.val>key){
root.left=deleteNode(root.left,key);
}
else if(root.val4.701. 二叉搜索树中的插入操作
这道题目不是很难，还是只要搞清楚每个节点该做什么以及什么时候做就行。思索一会儿就能知道这道题的what就是判断该节点的值和题目给的val，以及是否是空结点。when一般来说没有特殊情况都是在前序遍历的位置，上题目和代码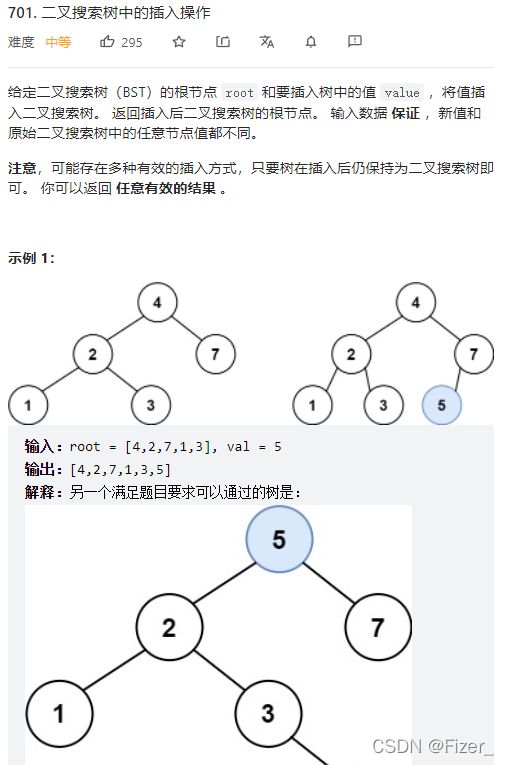
图上给的另一个满足要求的树需要对原有的树进行重构，在这里就不说了。最后附上代码：
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root==null) return new TreeNode(val); //如果是空树，则直接返回
findplace(root,val);
return root;
}
TreeNode findplace(TreeNode root,int val){
if(root==null) return new TreeNode(val);
if(root.val>val){
root.left=findplace(root.left,val);
}else if(root.val5.700. 二叉搜索树中的搜索
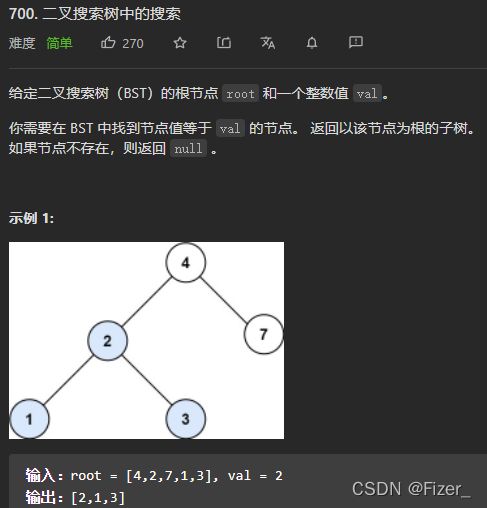这道题需要突破一下固有思维，原有的思维是该节点做什么以及什么时候做。但是这一题好像并不可以，但是我又说不上来到底是哪儿出了问题... 这道题的root不需要赋值，就直接返回即可，像上面那几道题都是用的root.left=xxx(root.left)之类的。
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if (root == null) {
return null;
}
// 去左⼦树搜索
if (root.val > val) {
return searchBST(root.left, val);
}
// 去右⼦树搜索
if (root.val < val) {
return searchBST(root.right, val);
}
return root;
}
}6.98. 验证二叉搜索树
这道题我最开始的想法是直接用中序遍历暴力获得这棵树的序列，然后依次进行比较看是否是升序，但是超出时间限制了。然后就想着怎么用递归的方法实现。最开始的是想着用一个最大值和最小值进行比较，但是始终没有很好的想明白该怎么比较，只知道左子树要小于根节点，右子树要大于根节点。当时一直纠结到底该怎么比较，转不过弯。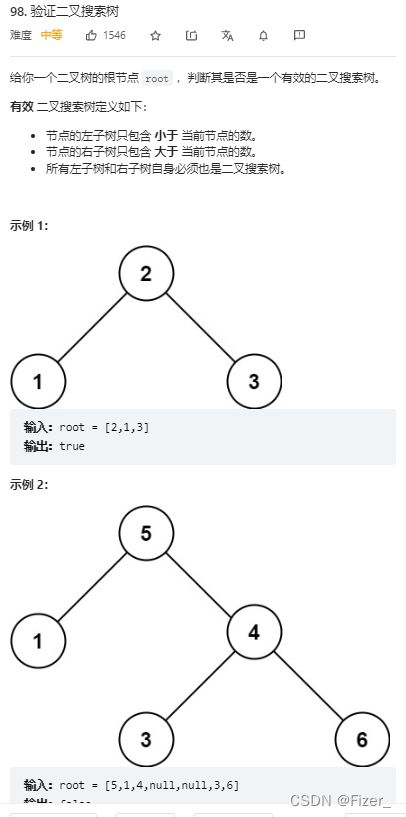
class Solution {
public boolean isValidBST(TreeNode root) {
return isValidBST(root,null,null);
}
boolean isValidBST(TreeNode root,TreeNode min,TreeNode max){
if(root==null) return true;
//左子树判断是否合法
if(max!=null&&root.val>=max.val) return false;
//右子树判断是否合法
if(min!=null&&root.val<=min.val) return false;
return isValidBST(root.left,min,root)&&isValidBST(root.right,root,max);
}
}这段代码的巧妙之处在于每次递归都只更行一个范围，而保持另一个不变。当更行左子树的时候，min永远是根节点，max是该节点的父节点；当更新右子树的时候，max永远是根节点，min是父节点。
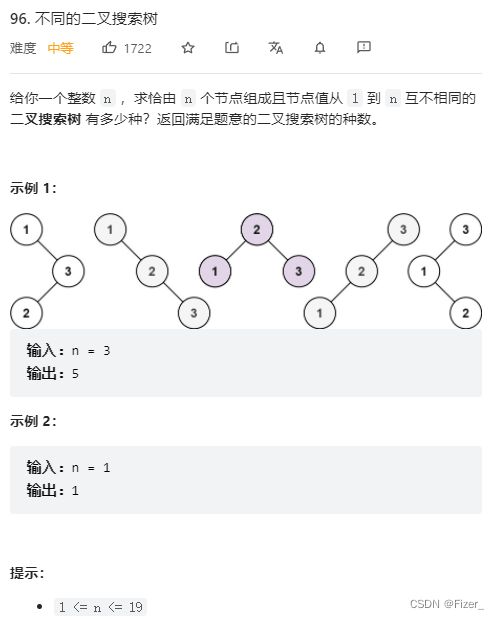
7.96. 不同的二叉搜索树
这种问题很明显就是穷举，用最笨的代码如下：
class Solution {
public int numTrees(int n) {
return count(1,n);
}
int count(int start,int end){
if(start>=end) return 1;
int res=0; //这里要注意每次都得清零
for (int i=start;i<=end;i++){
int left=count(start,i-1);
int right=count(i+1,end);
res+=left*right;
}
return res;
}
}还有一种带备忘录的方式，之前在东哥的算法笔记里面有讲过，代码如下：
class Solution {
int[][]memo; //备忘录
public int numTrees(int n) {
memo=new int [21][21];
return count(1,n);
}
int count(int start,int end){
if(memo[start][end]!=0) return memo[start][end]; 如果备忘录里面有值，则直接取出
if(start>=end) return 1;
int res=0;
for (int i=start;i<=end;i++){
int left=count(start,i-1);
int right=count(i+1,end);
res+=left*right;
}
memo[start][end]=res;
return res;
}
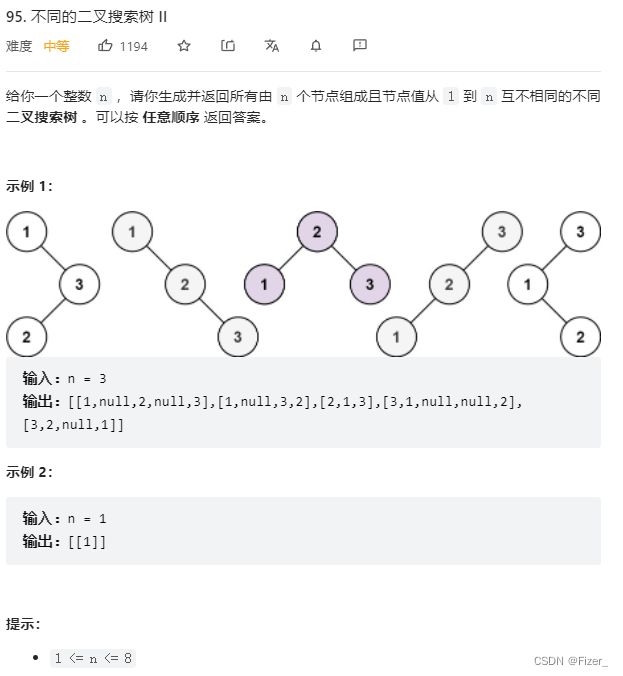
}8.95. 不同的二叉搜索树 II
这是上一题的升级版，会难很多。
class Solution {
public List generateTrees(int n) {
if (n == 0) return new LinkedList<>();
return gettree(1,n);
}
List gettree(int start,int end){
List res=new LinkedList<>();
if(start>end) {
res.add(null);
return res;
}
if(start==end){
TreeNode tree=new TreeNode(start);
res.add(tree);
return res;
}
for(int i=start;i<=end;i++){
List leftTree = gettree(start, i-1);
List rightTree = gettree(i+1, end);
for (TreeNode left : leftTree) {
for (TreeNode right : rightTree) {
TreeNode root = new TreeNode(i);
root.left = left;
root.right = right;
//加入到最终结果中
res.add(root);
}
}
}
return res;
}
} 9.938. 二叉搜索树的范围和
做了那么多难题，来道简单题练练手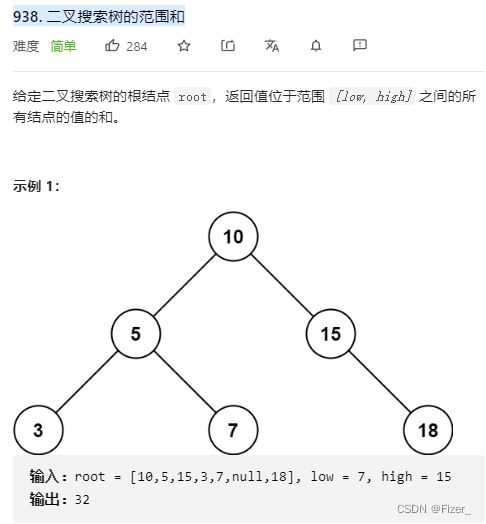
题目不难，那么要做的就是优化算法。我最开始的代码完全没用到二叉搜索树的性质，直接就做了，虽然做出来了但是时间和空间复杂度还是蛮高的：
class Solution {
int sum=0;
public int rangeSumBST(TreeNode root, int low, int high) {
getsum(root,low,high);
return sum;
}
void getsum(TreeNode root,int l,int h){
if(root==null) return ;
if(root.val>=l&&root.val<=h){
sum+=root.val;
}
getsum(root.left,l,h);
getsum(root.right,l,h);
}
}然后瞄了眼题解，有了以下代码：
class Solution {
public int rangeSumBST(TreeNode root, int low, int high) {
if(root==null) return 0;
if(root.val>=low&&root.val<=high)
return root.val+rangeSumBST(root.left,low,high)+rangeSumBST(root.right,low,high);
if(root.valhigh) return rangeSumBST(root.left,low,high);
return 0;
}
} 这段代码就用到了二叉搜索树的性质，当小于low的时候只需要遍历其右子树，同样当大于high的时候只需要遍历其左子树，当属于这个范围的时候就返回当前节点的值以及左子树和右子树的和。
10.530. 二叉搜索树的最小绝对差
这道题思路还是不难想的，根据二叉搜索树的左小右大的性质，对于每个节点，求得左子树的最大值和右子树的最小值，然后分别与当前节点的值计算得到差值然后比较即可。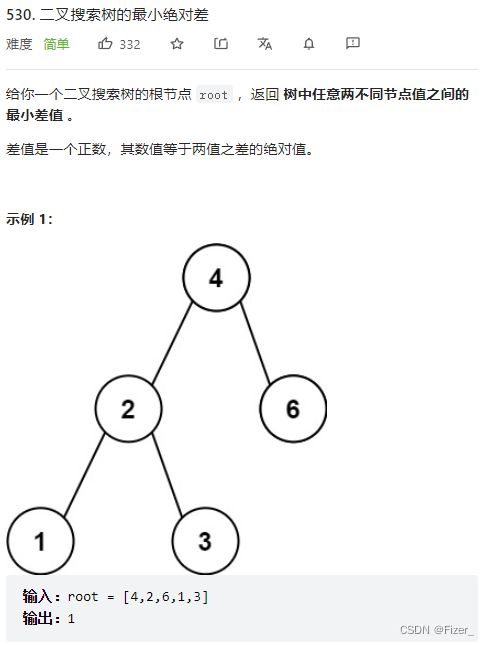
class Solution {
int min=Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
if(root==null) return 0;
int num1=0;
int num2=0;
if(root.left==null) num1=Integer.MAX_VALUE;
if(root.right==null) num2=Integer.MAX_VALUE;
if(root.left!=null){
num1=root.val-getleftmax(root.left);
}
if(root.right!=null){
num2=getrightmin(root.right)-root.val;
}
int ans=num1<=num2?num1:num2;
if(ans 这里有个小插曲，就是在答案正确以前提交了很多次都报错，最后查了一下原因是因为 if(root.left==null) num1=Integer.MAX_VALUE;
if(root.right==null) num2=Integer.MAX_VALUE;
这两段代码我之前的赋值为99，太小了所以报错，最后查看代码才发现错误，改成了max_value。
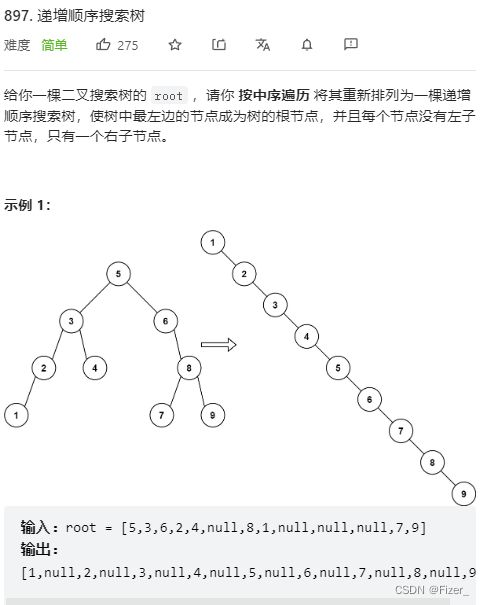
11.897. 递增顺序搜索树
这道题目在思想上非常简单，就是通过中序遍历得到顺序结点，然后创建一个新结点用来接收即可，但是在很多细节上还是需要注意。
class Solution {
List list = new ArrayList<>();
public TreeNode increasingBST(TreeNode root) {
dfs(root);
TreeNode dummy = new TreeNode(-1);
TreeNode cur = dummy; //指向dummy
for (TreeNode node : list) {
cur.right = node;
node.left = null;
cur = cur.right;
}
return dummy.right;
}
void dfs(TreeNode root) {
if (root == null) return ;
dfs(root.left);
list.add(root);
dfs(root.right);
}
} 这里用cur结点指向dummy，然后还有 node.left = null; 我试了发现如果去掉这句话会报错：Error - Found cycle in the TreeNode ，我想了想，觉得应该是用list存储的时候存储包括了当前节点，左子树结点和右子树结点，所以必须将左子树清零才可以。
12.173. 二叉搜索树迭代器
第一次做题目喝解释这么长的题，确实给我看了半天才看明白是个什么意思。这道题想让我们自己创建一个类，然后调用类的方法来实现。其实代码非常简单，我认为这道题目更多的在于考察自己写一个类的能力。
class BSTIterator {
private int p=0;
private List listroot;
public BSTIterator(TreeNode root) {
listroot=new ArrayList<>();
getlist(root);
}
public int next() {
return listroot.get(p++);
}
public boolean hasNext() {
if(p 13.剑指 Offer 36. 二叉搜索树与双向链表
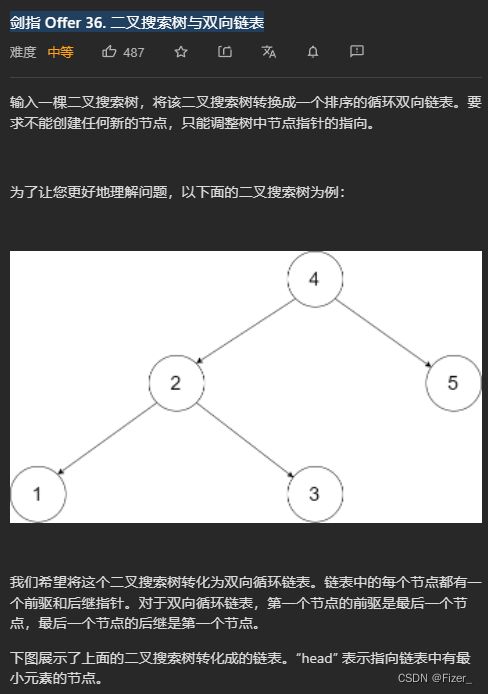这道题是二叉搜索树和双向循环链表的结合，执行起来还是在二叉搜索树中序遍历的前提下进行操作，用头节点head作为最后的输出，以及一个前节点pre作为当前节点的上一个结点，完成双向链表的操作。
class Solution {
Node pre,head;
public Node treeToDoublyList(Node root) {
if(root==null) return null;
traverse(root);
head.left=pre;
pre.right=head;
return head;
}
void traverse(Node root){
if(root==null) return ;
traverse(root.left);
if(pre==null) { //找到头节点
head=root;
pre=root;
}
else { //非头节点
pre.right=root;
root.left=pre;
pre=root;
}
traverse(root.right);
}
}14.109. 有序链表转换二叉搜索树
做过了这十几道二叉搜索树的题之后，现在遇到了这类题心里大概也是知道了该怎么做，但是在一些细节方面还是做的不是很好，就像接下来这题：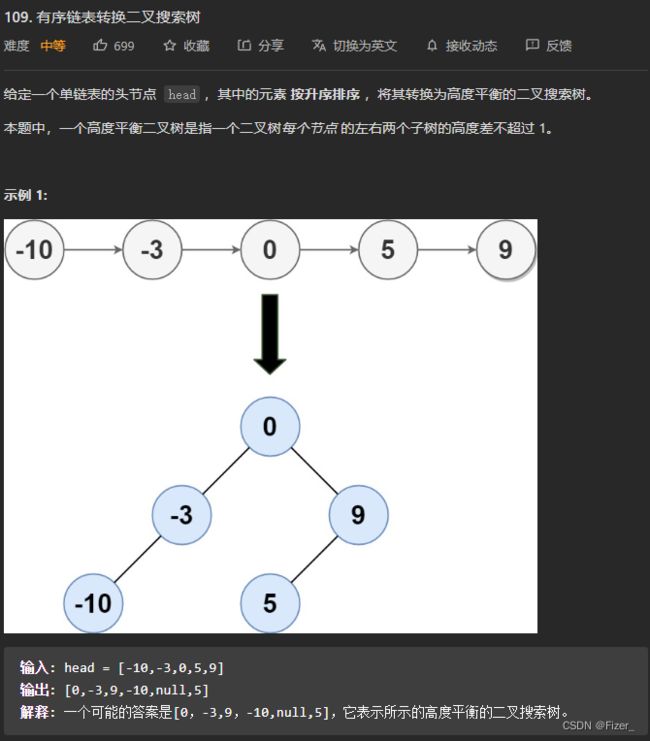
这道题需要将单链表转化为一个平衡二叉搜索树，所以很快就想到了用mid将链表分开然后对左右子树分别进行构造。我的代码比较杂乱，但是目的很明确，就是找到mid然后构造二叉树，代码如下：我的geimid方法就是先遍历一遍，得到链表的长度pnum，然后再用pnum得到中位数，然后创建一个mid结点来指向中位数这个结点
class Solution {
public TreeNode sortedListToBST(ListNode head) {
if(head==null) return null;
ListNode right=head;
while(right.next!=null){
right=right.next;
}
right=right.next;
return gettree(head,right);
}
TreeNode gettree(ListNode left,ListNode right){
if(left==right) return null;
ListNode mid=getmid(left,right);
TreeNode root=new TreeNode(mid.val);
root.left=gettree(left,mid);
root.right=gettree(mid.next,right);
return root;
}
ListNode getmid(ListNode left,ListNode right){
ListNode p=left;
int pnum=1;
while(p.next!=right){
pnum++;
p=p.next;
}
pnum=pnum/2+1;
ListNode mid=left;
while(pnum!=1){
pnum--;
mid=mid.next;
}
return mid;
}
}但是用时消耗以及内存占用都比较大，看了看题解，用到了一种快慢指针的方法，很巧妙，同时也极大的缩减了代码，如下：fast指针走两步，slow指针走一步，然后slow就是mid指针。这样就很快速的完成了寻找中位数的操作。
public ListNode getmid(ListNode left, ListNode right) {
ListNode fast = left;
ListNode slow = left;
while (fast != right && fast.next != right) {
fast = fast.next;
fast = fast.next;
slow = slow.next;
}
return slow;
}
15.669. 修剪二叉搜索树
第一眼看到这道题的时候我就想到了要用二叉搜索树的删除操作，试了很久但都没有得到正确的解，还是放弃了。这道题的解应该在删除二叉搜索树结点的前提下更进一步，由于是给了low和high这一个范围，故对于小于low的结点来书，其左子树和本身都要被删除，对于大于high的结点来说，其右子树和其本身都要被删除。这样一来代码就简单了很多。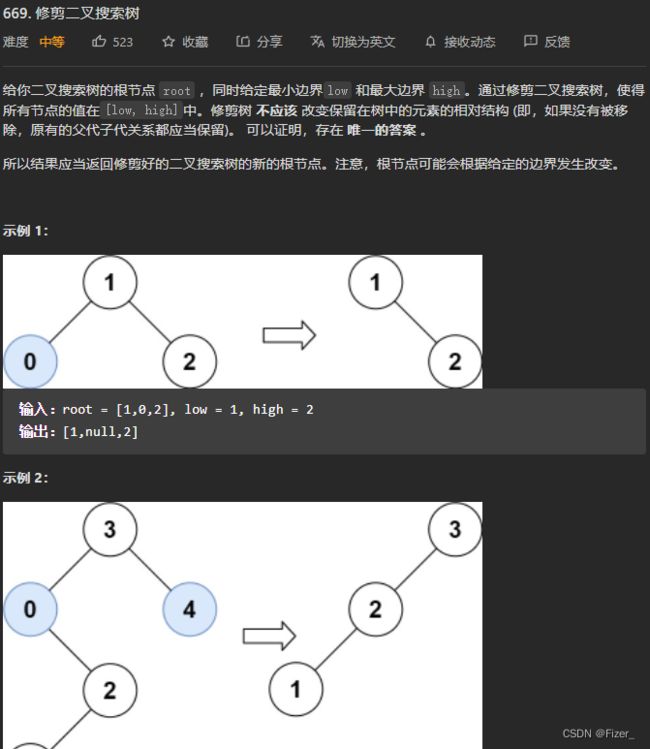
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root==null) return null;
if(root.valhigh) {
root=trimBST(root.left,low,high);
return root;
}
root.left=trimBST(root.left,low,high);
root.right=trimBST(root.right,low,high);
return root;
}
} 这里需要注意的是，对于trimBST这个函数而言，需要用treenode类型来接收其返回的值，这个我在一开始写的时候没有注意故出了很多错误 。
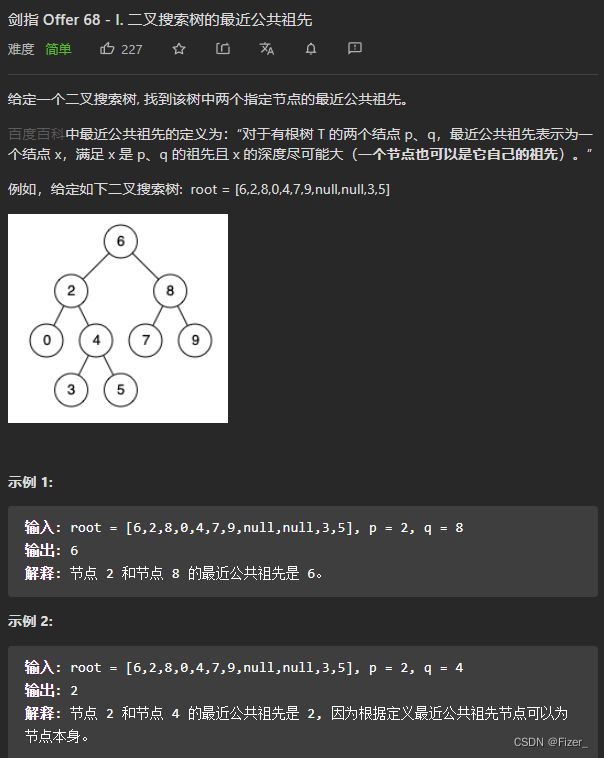
16.剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
每日一遍：我是sb。
这道题不是很难，一开始我以为p要小于q的，所以写下了如下代码：
class Solution {
TreeNode ans=new TreeNode();
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return null;
else if(root.val==p.val||root.val==q.val) {ans=root;return ans;}
else if(root.val>p.val&&root.val意思也很简单，就是如果满足root的值在p和q之间或者等于p或q的某个值，就返回。但是这道题并没有说pq的大小关系！所以得换思路，于是就有了下面这三行代码：
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.valroot.val&&q.val>root.val)
return lowestCommonAncestor(root.right,p,q);
return root;
}
} 17.剑指 Offer II 056. 二叉搜索树中两个节点之和
这道题也比较简单，感觉之前做过，就不多赘述了
class Solution {
int[] nums=new int[10001];
int i=0;
int flag=0;
public boolean findTarget(TreeNode root, int k) {
getk(root,k);
if(flag==1) return true;
return false;
}
void getk(TreeNode root,int k){
if(root==null) return ;
nums[i++]=k-root.val;
for(int j=0;j思想上和官解一样，都是存储k-root.val的值然后用当前结点与存好的值比较，其实就说哈希表，哈希表的使用方面我还不是很熟悉，还需加强，附上官解
class Solution {
Set set = new HashSet();
public boolean findTarget(TreeNode root, int k) {
if (root == null) {
return false;
}
if (set.contains(k - root.val)) {
return true;
}
set.add(root.val);
return findTarget(root.left, k) || findTarget(root.right, k);
}
}
哈希表的add方法和contains方法用的还是比较多的，需要多记一下。
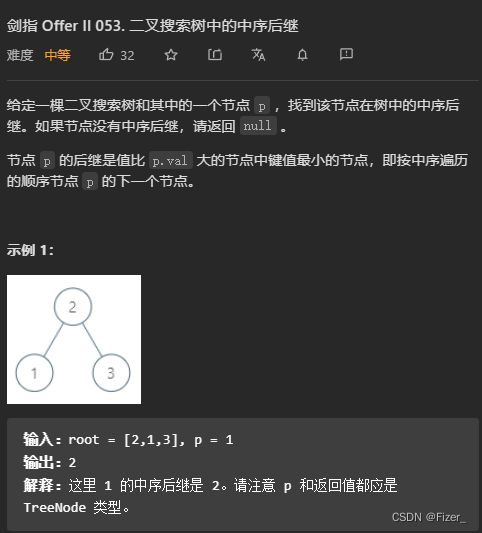
18.剑指 Offer II 053. 二叉搜索树中的中序后继
这道题在解题思路上也不是很难，但是代码实现上有些麻烦，
我的代码是先中序遍历将其赋值给一个整型数组，然后用rank记录值等于p的下一个位置，然后再中序遍历一次找到值等于rank的root并返回：
class Solution {
int[] nums=new int[10001];
int i=0;
int rank=0;
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
if(root==null) return null;
tonums(root,nums,p);
int ans=nums[rank];
if(nums[rank]==0) {
return null;
}
return getp(root,ans);
}
void tonums(TreeNode root,int[] nums,TreeNode p){
if(root==null) return ;
tonums(root.left,nums,p);
nums[i++]=root.val;
if(root.val==p.val) rank=i;
tonums(root.right,nums,p);
}
TreeNode getp(TreeNode root,int ans){
if(root==null) return null;
if(root.val==ans) return root;
if(root.val>ans) return getp(root.left,ans);
if(root.val然后看了眼题解，虽然题解的代码很简单而且思路也很清晰但是时间和空间复杂度倒是差不太多，但是都没用到递归，这倒是我要学习的，也附上代码：
class Solution {
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
TreeNode ans = null;
while(root != null)
{
if(root.val > p.val)
{
ans = root;
root = root.left;
}
else
root = root.right;
}
return ans;
}
}
若当前节点值小于等于p节点值，则向右子树寻找，若当前节点值大于p节点值，
则该节点可能为p的中序后继，但需要继续向左子树寻找是否有更小的19.剑指 Offer 54. 二叉搜索树的第k大节点
这道题好像在哪儿做过，就是中序遍历的时候先遍历右子树，再遍历左子树即可
class Solution {
int ans;
int index;
public int kthLargest(TreeNode root, int k) {
index=k;
root=getk(root,k);
return ans;
}
TreeNode getk(TreeNode root,int k){
if(root==null) return null;
root.right=getk(root.right,k);
if(index==1) {ans=root.val;}
index--;
root.left=getk(root.left,k);
return root;
}
}
2022.5.9-5.22
1.剑指 Offer 33. 二叉搜索树的后序遍历序列
这道题一开始并没有想到解题思路，但是之前做过类似的题目，知道需要分左子树和右子树，但是没有找到分界点的那个值，所以看了眼答案
class Solution {
public boolean verifyPostorder(int[] postorder) {
return verifyPostorder(postorder,0,postorder.length-1);
}
boolean verifyPostorder(int[] nums,int start,int end){
if(start>=end) return true;
int p=start;
while(nums[p]nums[end]) p++;
return p==end&&verifyPostorder(nums,start,m-1)&&verifyPostorder(nums,m,end-1);
}
} 杠看完答案还有一点不太明白的是为什么需要加一个p==end，然后想想，这是在判断右子树。
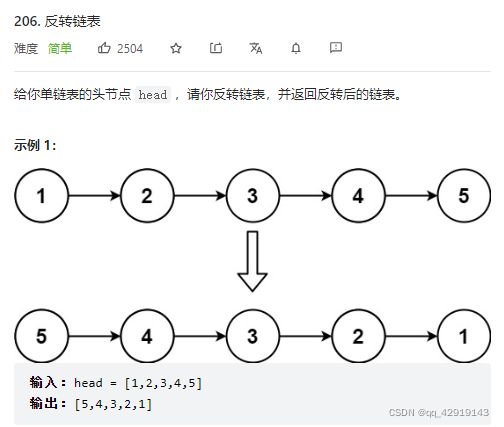
2.206. 反转链表
这道题想法还是不难的，主要是有些小细节需要注意。
我是先做了反转链表2，发现不太好做就先做做看这道题，难度不大，待会儿就去吧2给解决了。
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null) return null;
ListNode p = head;
ListNode pre = head;
while(p.next!=null){
pre = p;
p = p.next;
}
ListNode ans = p;
while(p!=head){
p.next = pre;
p = pre;
ListNode q = head;
while(q.next!=pre){
q = q.next;
}
pre = q;
}
p.next = null;
return ans;
}
}想法就是不断向前迭代pre和p指针即可。
5.22更行：复习这周的题目，写了一个更简单的版本
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) return head;
ListNode p,pre,post;
p = head;
pre = p.next;
p.next = null; //由于p最后将成为尾结点，
//故需要将p.next设为null，
//否则将成环
while(pre != null){
post = pre.next;
pre.next = p;
p = pre;
pre = post;
}
return p;
}
}3.92. 反转链表 II
这道题是上一题的升级版，在一段链表的中间进行反转，难度确实有所上升但是基本代码还是不变，多了很多细节（就我自己写的代码而言）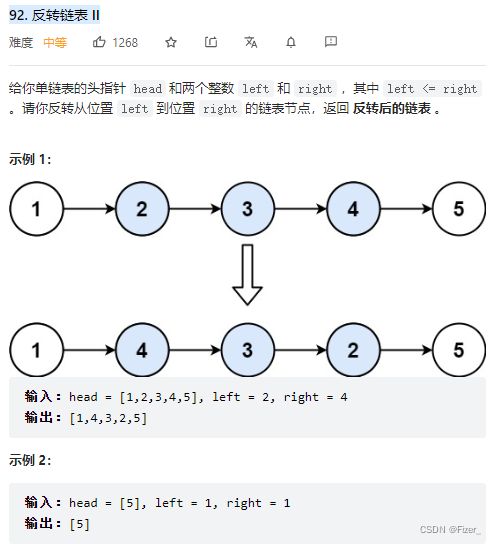
我的代码还要考虑left是否在起始点，代码很长，所以还是要多看题解。
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
if(head==null) return null;
if(left == right) return head;
ListNode pre = head;
ListNode p = head;
while(right!=1){
pre = p;
p=p.next;
right--;
}
ListNode end = p.next;
ListNode start = head;
ListNode leftnode = head;
while(left!=1){
start = leftnode;
leftnode = leftnode.next;
left--;
}
if(start == leftnode){
start = p;
while(p!=leftnode){
p.next = pre;
p = pre;
ListNode q = leftnode;
while(q.next!=pre){
q = q.next;
}
pre = q;
}
p.next = end;
return start;
}
else {
start.next = p;
}
while(p!=leftnode){
p.next = pre;
p = pre;
ListNode q = leftnode;
while(q.next!=pre){
q = q.next;
}
pre = q;
}
p.next = end;
return head;
}
}这应该是我写过最长的代码了哈哈哈，但是很多重复的部分有待改进。
4.82. 删除排序链表中的重复元素 II
这道题的简单版我之前就做过了，所以这道题也没花很长时间就做出来了，果然做完树的题目再做这种链表题目会简单很多。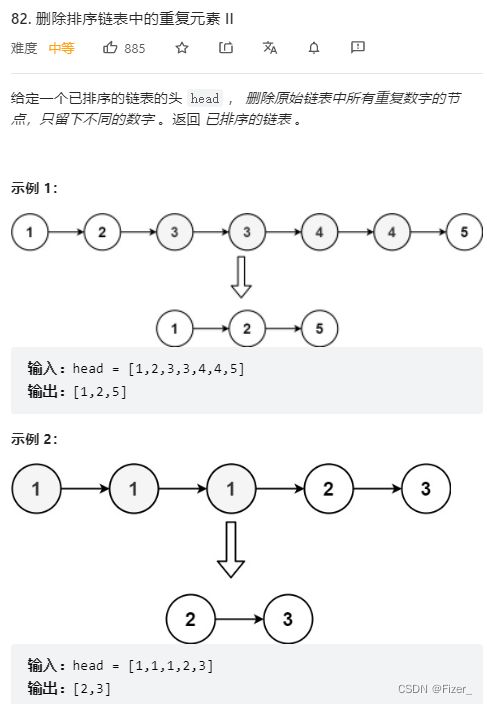
这道题和简单版的就多了个把所有重复元素删除的操作，因此需要加一个pre结点，用来指向最后那个不重复的结点。赴上代码：
class Solution {
public ListNode deleteDuplicates(ListNode head) {
if(head==null) return null;
ListNode dummynode = new ListNode(-1);
dummynode.next = head;
ListNode pre = dummynode;
ListNode p = head;
ListNode q = p.next;
while(q != null) {
if(p.val != q.val){
pre = p;
p = q;
q = q.next;
} else {
while(p.val == q.val){
q = q.next;
if(q == null) {
pre.next = null;
break;
}
}
if(q!=null){
pre.next = q;
p = q;
q = q.next;
}
}
}
return dummynode.next;
}
}好像链表题目的代码都比较长，不用递归确实写起来很简单但是长度长一些。
5.19. 删除链表的倒数第 N 个结点
链表的题目写起来都不算很难，不过在一些细节方面确实需要注意以下不然容易出bug。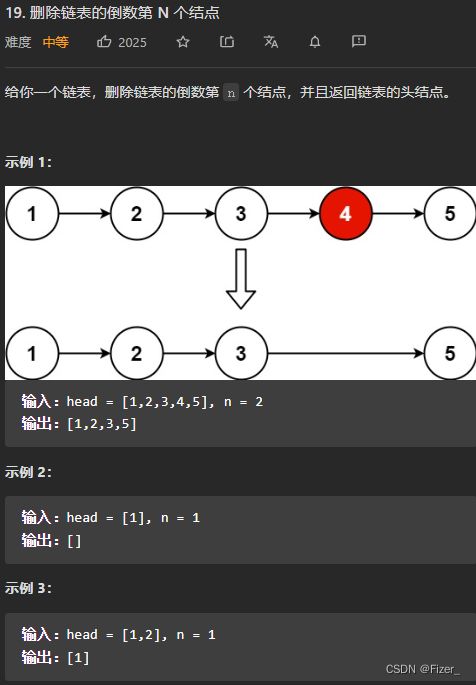
这道题需要注意的又两个小点，1是当链表只有一个结点的时候，直接返回null，2是当删除的是头节点的时候，就不用while去找那个结点，直接用dummy指向头节点的下一个结点即可：
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if(head == null) return null;
ListNode dummy = new ListNode(-1);
dummy.next = head;
int num = 1;
while(head.next != null){
head = head.next;
num++;
}
if(num==1) return null; //链表只有一个节点的情况
int deletenum = num - n + 1;
head = dummy.next;
if(deletenum == 1) { //删除的是头节点的情况
dummy.next = head.next;
return dummy.next;
}
ListNode pre = head;
while(deletenum != 1){
pre = head;
head = head.next;
deletenum--;
}
pre.next = head.next;
return dummy.next;
}
}6.2. 两数相加
我认为这道题的难点就在于进位，以及进位以后该如何操作。然后又分为两种情况，一种情况是两个链表长度一样，另一种是不一样。对于一样长的链表，任选一条链表作为被加数，若最后一个链表上的值有进位，则在最后一个链表后再新建一个链表，值为一。对于不一样长的链表，则需要考虑一直进位的问题，如999+999999这个问题，因为要一直进位直到最后一个，所以在while循环里面还需要一个while。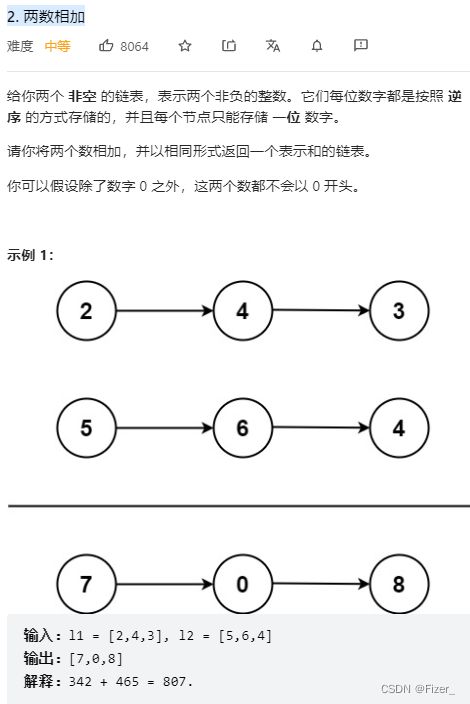
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode l1node = l1;
ListNode l2node = l2;
ListNode dummy = new ListNode (-1);
int flag = findflag(l1node,l2node); // 分三种情况
int account = 0;
if(flag == 0){
dummy.next = l1;
while(l1.next != null){
l1.val = l1.val + l2.val +account;
if(l1.val >= 10){
l1.val = l1.val % 10 ;
account = 1;
}
else{
account = 0;
}
l1 = l1.next;
l2 = l2.next;
}
l1.val = l1.val + l2.val + account;
if(l1.val >= 10){
l1.val = l1.val % 10 ;
l1.next = new ListNode (1);
}
}
if(flag > 0){
return addlist(l1,l2,dummy,account);
}
if(flag < 0){
return addlist(l2,l1,dummy,account);
}
return dummy.next;
}
int findflag (ListNode l1, ListNode l2){
int num1 = 1;
int num2 = 1;
while(l1.next != null){
l1 = l1.next;
num1++;
}
while(l2.next != null){
l2 = l2.next;
num2++;
}
return num1-num2;
}
ListNode addlist (ListNode l1, ListNode l2, ListNode dummy, int account){
dummy.next = l1;
while(l2.next != null){
l1.val = l1.val + l2.val +account;
if(l1.val >= 10){
l1.val = l1.val % 10 ;
account = 1;
}
else{
account = 0;
}
l1 = l1.next;
l2 = l2.next;
}
l1.val = l1.val + l2.val + account;
while(l1.val >= 10){
l1.val = (l1.val ) % 10 ;
if(l1.next == null){
l1.next = new ListNode(1);
break;
}
l1 = l1.next;
l1.val += 1;
}
return dummy.next;
}
}7.24. 两两交换链表中的节点
这道题也不算难，做了大概十道链表的题，基本上就是交换，删除，增加，相加这些题型，和树比简单很多。这道题就是交换链表的题目，唯一需要注意的就是要多加一个指针，不然容易返回乱七八糟的链表。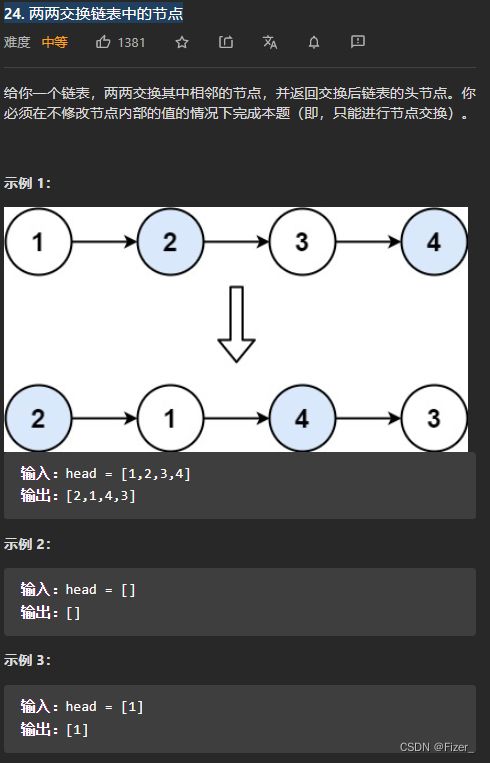
class Solution {
public ListNode swapPairs(ListNode head) {
if(head == null || head.next == null) return head;
ListNode dummy = new ListNode(-1);
ListNode ppre = dummy;
ListNode pre = head;
ListNode p = pre.next;
dummy.next = head;
while(pre != null && p != null){
pre.next = p.next;
p.next = pre;
ppre.next = p;
ppre = pre;
pre = pre.next;
if(pre != null && pre.next != null){
p = pre.next;
} else break;
}
return dummy.next;
}
}这里用ppre，pre，p进行指针之交换，用dummy指向这个head，一开始我没用ppre，直接对dummy操作，然后然会head，结果会少一个数字，原因就是head一开始就从第一个位置交换到了第二个位置，这里我想了一小会儿。
8.61. 旋转链表
第一眼看到这题想到的是用迭代或者递归把每个结点都移动到指定位置，但是仔细看完之后发现只需要两个操作即可，第一步是将最后一个结点的next指向head，然后把断点处的next设为null即可
class Solution {
public ListNode rotateRight(ListNode head, int k) {
if( k == 0 || head == null) return head;
ListNode dummy = new ListNode();
ListNode p = head;
int length = 1;
while(p.next != null){
p = p.next;
length += 1;
}
if(length == 1) return head;
if(k % length == 0 || length == k) return head;
if(length < k) {
k = k % length;
}
k = length - k;
p.next = head;
ListNode q = head;
while(k >1){
q = q.next;
k -= 1;
}
dummy = q.next;
q.next = null;
return dummy;
}
}9.141. 环形链表
其实昨天看这道题的时候没有想好要怎么写，今天看了一篇总结链表题解的文章才写出代码，这道题用的还是快慢指针的思想，即如果fast喝slow能相遇，那么一定存在环，否则fast一定会指向null，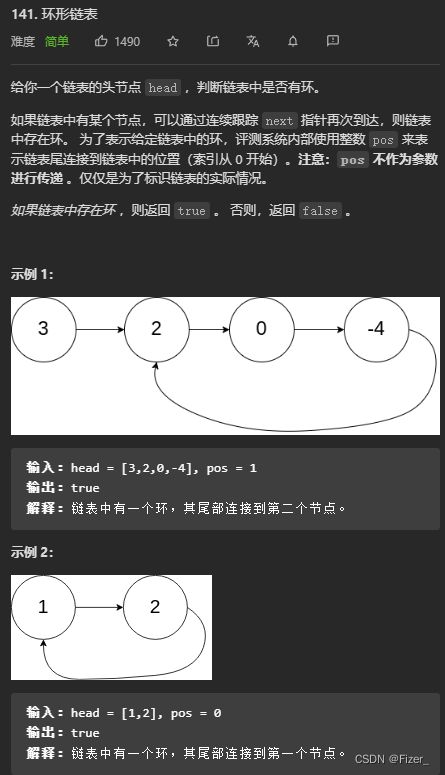
public class Solution {
public boolean hasCycle(ListNode head) {
if (head == null) return false;
ListNode fast = head;
ListNode slow = head;
fast = head.next;
if(fast == null ) return false;
while(fast != slow){
if(fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
}
else return false;
}
return true;
}
}10.283. 移动零
随便找了题保持手感，可惜我自己的代码还是出了bug...
这道题复习了一下快慢指针，先将所有不为零的数字按顺序排好，直到right到顶，然后从left开始全部补零即可。
class Solution {
public void moveZeroes(int[] nums) {
int left = 0, right = 0;
while(right11.232. 用栈实现队列
这道题思想上不是很难，主要是不知道该怎么写。看完答案之后大概知道这类题目的写法了。
class MyQueue {
private Stack s1,s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
public void push(int x) {
s1.push(x);
}
public int pop() {
peek();
return s2.pop();
}
public int peek() {
if(s2.isEmpty()){
while(!s1.isEmpty()){
s2.push(s1.pop());
}
}
return s2.peek();
}
public boolean empty() {
return s2.isEmpty()&&s1.isEmpty();
}
} 12.225. 用队列实现栈
这题和上一题类似，不过是用两个队列实现栈，主要是pop操作的时候，需要用q2接收，同时改变topele元素（即栈顶元素）。
class MyStack {
private Queue q1 = new LinkedList<>();
private Queue q2 = new LinkedList<>();
private int topele = 0;
public MyStack() {
}
public void push(int x) {
q1.offer(x);
topele = x;
}
public int pop() {
int nums = 0;
while(q1.peek() != topele && q1.isEmpty()==false){
nums = q1.peek();
q2.offer(q1.poll());
}
int last = q1.poll();
topele = nums;
q1 = q2;
return last;
}
public int top() {
return topele;
}
public boolean empty() {
return q1.isEmpty();
}
} 13.11. 盛最多水的容器
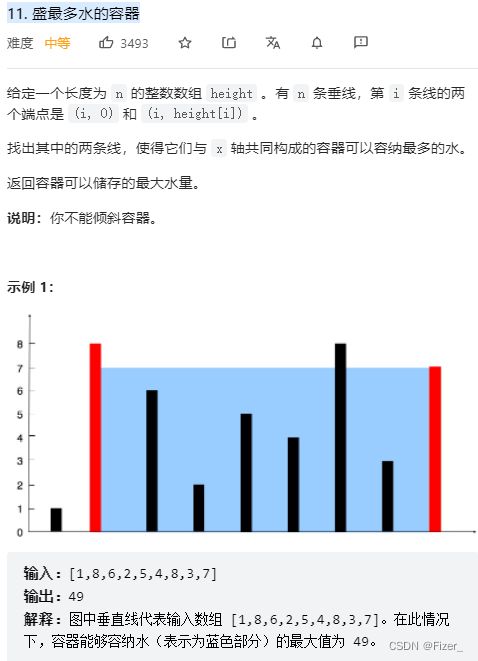这道题还挺有意思的，算是比较简单的应用题吧，关键是找到“短板”。我一开始的思路就是直接两个for暴力解决，事实上也应该是可行的，但是超时了，那么就换呗。提前固定水杯的两端，并找到短板。需要注意的是，每次移动的时候一定是移动较短的那一条边。因为首先不管是移动那一条边，宽度一定是-1的，其次移动短边，长边不受影响，下一个短边更长则面积可能更长，但是移动长边的话，短边不变，面积一定会减少。那么这样就好办了，一个while就解决了，上代码：
class Solution {
public int maxArea(int[] height) {
int p1 = 0;
int p2 = height.length-1;
int temp = 0;
int max = 0;
while(p2>p1){
int width = p2 - p1;
int smallnum = height[p1]max) {max = temp;}
if(height[p1]<=height[p2]){p1++;}
else {p2--;}
}
return max;
}
} 14.496. 下一个更大元素 I
这道题学会了一个新的知识点——单调栈，还是挺巧妙的，想题目中有什么下一个最大元素之类的题目都能用得上
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Stack s = new Stack<>();
//map:key--->value:nums2[i]--->下标i之后第一个比nums2[i]大的元素（若不存在，则置为-1）
Map map = new HashMap<>();
for(int i = nums2.length - 1; i >= 0; i--){
while(!s.empty() && s.peek() <= nums2[i]){//栈顶只要小于待入栈元素就不断出栈，
循环退出条件是栈顶元素大于nums2[i]，这样在入栈之后才能保持单调栈的情况
s.pop();//持续出栈，构造单调栈
}
map.put(nums2[i],s.empty() ? -1 : s.peek());//map中记录对应的映射
s.push(nums2[i]);//入栈
}
for(int i = 0; i < nums1.length; i++){
nums1[i] = map.get(nums1[i]);
}
return nums1;
}
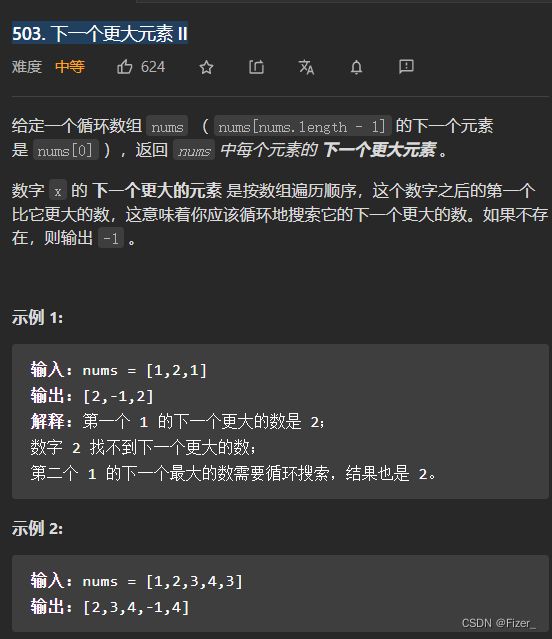
} 15.503. 下一个更大元素 II
这是上一题的加强版，也算是对单调栈的一种巩固，还学到一个新的知识点，就是用%运算来模拟环，即(i%nums.length-1)
class Solution {
public int[] nextGreaterElements(int[] nums) {
int []res = new int[nums.length];
Stack s = new Stack<>();
for(int i = 2*nums.length-1;i>=0;i--){
while(!s.empty()&&nums[i%nums.length]>=s.peek()){
s.pop();
}
res[i%nums.length]=s.empty()?-1:s.peek();
s.push(nums[i%nums.length]);
}
return res;
}
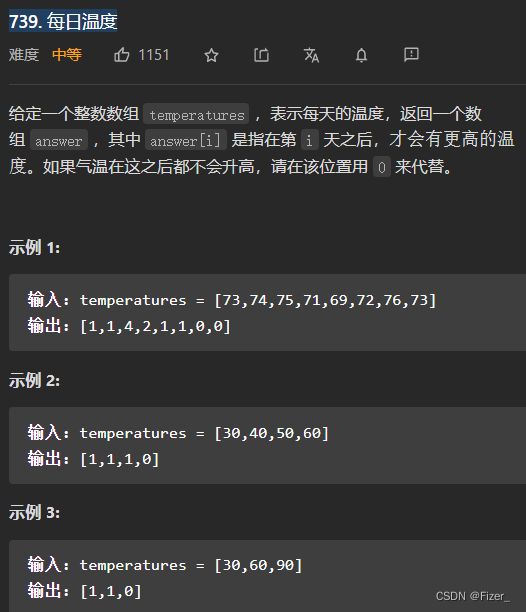
} 16.739. 每日温度
这题还是单调栈的题目，换汤不换药，只是将存进栈中的元素换成了索引。
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
Stack s = new Stack<>();
int [] res = new int[temperatures.length];
for(int i = temperatures.length-1;i>=0;i--){
while(!s.empty()&&temperatures[i]>=temperatures[s.peek()]){
s.pop();
}
res[i]=s.empty()?0:s.peek()-i;
s.push(i);
}
return res;
}
} 17.3. 无重复字符的最长子串
今天不想跟着东哥写了，按顺序挑了一题写写，难度还是不大的，用一个list加一个循环就可以完成
但是看完题解之后发现只是一道滑动窗口的题目，在执行时间上面少了很多，学了一个新的知识点。
class Solution {
public int lengthOfLongestSubstring(String s) {
if(s.length()==0) return 0;
int max = Integer.MIN_VALUE;
for(int i=0;i list = new ArrayList<>();
int j=i+1;
list.add(s.charAt(i));
int num = 1; //只有一个元素的时候就是1
while(jmax){max=num;}
}
return max;
}
} 18.187. 重复的DNA序列
接着上午的滑动窗口继续写了一道题。个人认为难度要比上午那一题还要低一些，因为窗口的大小固定，只需要滑动即可。
class Solution {
public List findRepeatedDnaSequences(String s) {
ArrayList ans = new ArrayList<>();
HashMap map = new HashMap<>();
int len = s.length();
if(len<10) return ans;
int left = 0;
while(left+10<=len){
String sub = s.substring(left,left+10);
int num = map.getOrDefault(sub,0);
if(num==1) {
ans.add(sub);
}
map.put(sub,num+1);
left++;
}
return ans;
}
} 下面是我第一次写的代码，我认为是没什么问题的，但是超时了，也贴上来吧
class Solution {
public List findRepeatedDnaSequences(String s) {
ArrayList ans = new ArrayList<>();
ArrayList temp = new ArrayList<>();
int len = s.length();
if(len<10) return ans;
int left = 0;
String sub = s.substring(left,left+10);
while(left+10 我的想法是用一个暂存list“temp”来记录每个窗口的值，然后如果出现超过一次就加入答案list“ans”，应该是因为两次contains操作导致超时。
19.80. 删除有序数组中的重复项 II
最近做题老是没有思路，知道要用什么方法但写不出来，看来还是需要，准备接下来几天复习一下写过的题目。
class Solution {
public int removeDuplicates(int[] nums) {
int n = nums.length;
if (n <= 2) {
return n;
}
int slow = 2, fast = 2;
while (fast < n) {
if (nums[slow - 2] != nums[fast]) {
nums[slow] = nums[fast];
++slow;
}
++fast;
}
return slow;
}
}2022.5.23-2022.6.5
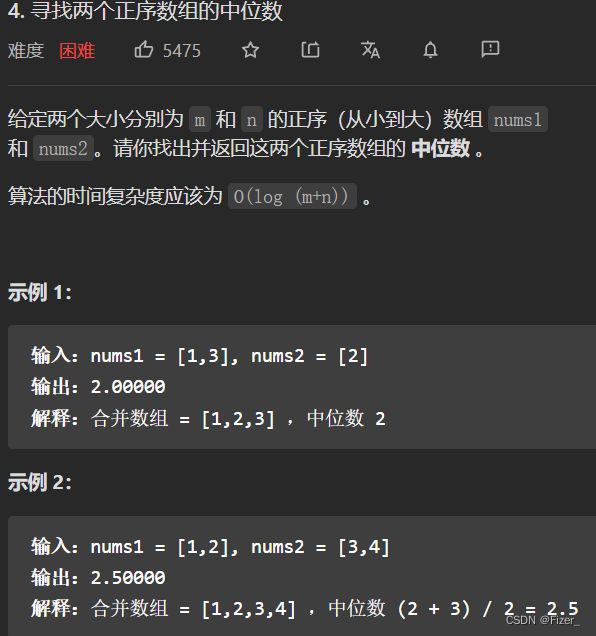
1.4. 寻找两个正序数组的中位数
这道题如果不用归并排序还是挺难的，但是如果不用归并排序，我尝试了很多方法，都会有各种bug或者一些小细节我没有考虑到，所以还是算了吧。
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
int [] sum =new int[m+n];
int p = 0 , q = 0 , w = 0;
double ans = 0;
while(p2.15. 三数之和
这道题我最开始的想法就是三个for，效率很低但是理论上应该是可行的。优化方案是先将数组排序然后固定第一个数，直到遇见0为止。利用双指针start和end进行比较，不过需要注意的是重复问题，这里start，end和i都需要去重。
class Solution {
public List> threeSum(int[] nums) {
int len = nums.length;
List> list = new ArrayList();
Arrays.sort(nums);
int end = len - 1;
int i = 0;
if(len<3) return list;
while(i0){
end--;
}else if(nums[i]+nums[start]+nums[end]==0){
//list.add(nums[i],nums[start],nums[end]);
list.add(Arrays.asList(nums[i],nums[start],nums[end]));
while (start