读书笔记 - 数据结构与算法javascript描述
一 数组
数组:元素可以通过索引来任意存取,索引通常是数字,用力啊计算元素之间存储位置的偏移量。
JavaScript 中的数组是一种特殊的对象,用来表示偏移量的索引是该对象的属性,索引可 能是整数。然而,这些数字索引在内部被转换为字符串类型,这是因为 JavaScript 对象中 的属性名必须是字符串。数组在 JavaScript 中只是一种特殊的对象,所以效率上不如其他 语言中的数组高。
数组使用
// 创建数组
var arr = [] // []
var arr1 = new Array(10) // 指定数组的长度 [empty × 10]
var arr1 = new Array(1,2,3)// [1,2,3]
// 数组的长度
arr.length
// 判断是否是数组
Array.isArray(arr)
// 字符串生成数据:
var string1 = "hello world"
string1.split(" ") // ['hello', 'world']
存储函数:
// 查找元素:indexOf
indexOf() 函数是最常用的存取函数之一,用来查找传进来的参数在目标数组中是否存在
// 数组的字符串表示:join, toString
var names =['liz','aimi', 'lucy']
names.join("|") // 'liz|aimi|lucy'
names.toString() // 'liz,aimi,lucy'
// 由已有数组创建新数组 concat, splice
concat() 和 splice() 方法允许通过已有数组创建新数组。concat 方法可以合并多个数组 创建一个新数组,splice() 方法截取一个数组的子集创建一个新数组。
可变数组
1. 为数组添加元素 push:在数组尾部添加元素,unshift:在数组头部添加元素.返回值都为数组的长度
var nums = [1,2,3,4,5]
nums.push(6);
nums.unshift(7)
2.从数组中删除元素 pop:删除尾部元素, shift:删除头部元素。返回值都是:被删除的元素,数组的长度-1
var nums = [1,2,3,4,5,9];
nums.pop() // 9
nums.shift() // 1
3.从数组中间位置添加和删除元素 splice:添加时:返回空数组,但是原来的数组变了。删除:返回删除的元素,但是原来的数组也变了。
使用 splice() 方法为数组添加元素,需提供如下参数:
• 起始索引(也就是你希望开始添加元素的地方);
• 需要删除的元素个数(添加元素时该参数设为 0);
• 想要添加进数组的元素。
var nums = [1,2,3,7,8,9];
中间位置添加:
nums.splice(3,0,12) // []
console.log(nums)//[1, 2, 3, 12, 7, 8, 9]
中间位置删除:
nums.splice(3,1,) // [12]
console.log(nums)//[1, 2, 3, 7, 8, 9]
4.为数组排序 reverse, sort
- 数组的迭代器方法
不生成新数组的迭代器方法:
forEach
every
some
reduce
reduceRight
生成新数组的迭代器方法:
map,
filter
二维数组和多维数组
二维数组类似一种由行和列构成的数据表格。在 JavaScript 中创建二维数组,需要先创建 一个数组,然后让数组的每个元素也是一个数组。最起码,我们需要知道二维数组要包含 多少行,有了这个信息,就可以创建一个 n 行 1 列的二维数组了
- 处理二维数组的元素:
var grades = [[89, 77, 78],[76, 82, 81],[91, 94, 89]];
var total = 0; var average = 0.0;
for (var row = 0; row < grades.length; ++row) {
for (var col = 0; col < grades[row].length; ++col) {
total += grades[row][col]
}
average = total / grades[row].length;
alert("Student " + parseInt(row+1) + " average: " + average.toFixed(2));
total = 0;
average = 0.0;
}
内层循环由下面这个表达式控制:col < grades[row].length
- 参差不齐的数组
参差不齐的数组是指数组中每行的元素个数彼此不同。有一行可能包含三个元素,另一行 可能包含五个元素,有些行甚至只包含一个元素。很多编程语言在处理这种参差不齐的数 组时表现都不是很好,但是 JavaScript 却表现良好,因为每一行的长度是可以通过计算得 到的。
var grades = [[89, 77],[76, 82, 81],[91, 94, 89, 99]];
var total = 0; var average = 0.0;
for (var row = 0; row < grades.length; ++row) {
for (var col = 0; col < grades[row].length; ++col) { // grades[row].length: 可以得到数组的长度
total += grades[row][col];
}
average = total / grades[row].length;
alert("Student " + parseInt(row+1) + " average: " + average.toFixed(2));
total = 0;
average = 0.0;
}
- 对象数组
var arr = [{ x: 1, y:2} , {x: 3, y}]
- 对象中的数组
在对象中,可以使用数组存储复杂的数据。本书中讨论的很多数据都被实现成一个对象, 对象内部使用数组保存数据。
二 列表
在日常生活中,人们经常使用列表:待办事项列表、购物清单、十佳榜单、最后十名榜单 等。计算机程序也在使用列表,尤其是列表中保存的元素不是太多时。当不需要在一个很 长的序列中查找元素,或者对其进行排序时,列表显得尤为有用。反之,如果数据结构非 常复杂,列表的作用就没有那么大了。
列表是一组有序的数据。每个列表中的数据项称为元素。在 JavaScript 中,列表中的元素 可以是任意数据类型。列表中可以保存多少元素并没有事先限定,实际使用时元素的数量 受到程序内存的限制。
不包含任何元素的列表称为空列表。列表中包含元素的个数称为列表的 length。在内部实 现上,用一个变量 listSize 保存列表中元素的个数。可以在列表末尾 append 一个元素, 也可以在一个给定元素后或列表的起始位置 insert 一个元素。使用 remove 方法从列表中 删除元素,使用 clear 方法清空列表中所有的元素。
还可以使用 toString() 方法显示列表中所有的元素,使用 getElement() 方法显示当前元素。
列表拥有描述元素位置的属性。列表有前有后(分别对应 front 和 end)。使用 next() 方 法可以从当前元素移动到下一个元素,使用 prev() 方法可以移动到当前元素的前一个元 素。还可以使用 moveTo(n) 方法直接移动到指定位置,这里的 n 表示要移动到第 n 个位置。 currPos 属性表示列表中的当前位置。
列表的抽象数据类型并未指明列表的存储结构,在本章的实现中,我们使用一个数组 dataStore 来存储元素。
实现列表类:
function List() {
this.listSize = 0
this.ps = 0
this.dataSource = [] // 初始化一个空数组来保存列表元素
this.clear = clear
this.find = find
this.toString = toString
this.insert = insert
this.append = append
this.remove = remove
this.front = front
this.end = end
this.prev= prev
this.next = next
this.length = length
this.currPos = currPos
this.moveto = moveto
this.getElement = getElement
this.contains = contains
}
append: 给列表添加元素
function append(element) {
this.datasource[this.listSize++] = element
}
remove: 从列表中删除元素
function remove(element) {
const index = find(element)
if (index > -1) {
this.listSize.splice(index, 1)
-- this.listSize
return true
}
return false
}
find:在列表中查找某一个元素
function find(element) {
for (var i = 0; i < this.dataSource.length; i++) {
if (this.dataSource[i] === element) {
return i
}
}
return -1
}
length:列表中有多少个元素
function length() {
return this.listSize
}
toString: 显示列表中的元素
function toString() {
return this.dataSource
}
insert:向列表中添加一个元素:插入到某个元素之后
function insert(element, after) {
var index = this.find(after)
if (index > -1) {
this.dataSource.splice(after, 0, element)
++this.listSize
return true
}
return false
}
clear:清空列表
function clear() {
delete this.dataSource
this.dataSource = []
this.lisSize = this.pos = 0
}
contaons:判断给定值是否在列表中
function contaons(element) {
if (this.find(element) > -1) return true
retun false
}
遍历列表:
三 栈
四 队列
五 链表
JavaScript 中数组的主要问题是,它们被实现成了对象,与其他语言(比如 C++ 和 Java) 的数组相比,效率很低。
如果你发现数组在实际使用时很慢,就可以考虑使用链表来替代它。除了对数据的随机访 问,链表几乎可以用在任何可以使用一维数组的情况中。如果需要随机访问,数组仍然是 更好的选择。
定义链表
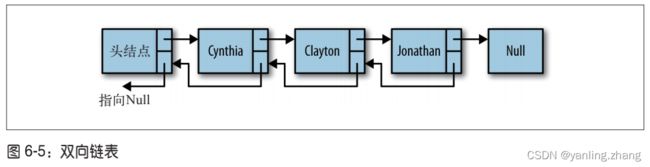
链表是由一组节点组成的集合。每个节点都使用一个对象的引用指向它的后继。指向另一 个节点的引用做链。
链表的结构如下:

数组元素靠它们的位置进行引用,链表元素则是靠相互之间的关系进行引用。
遍历链表,就是跟着 链接,从链表的首元素一直走到尾元素(但这不包含链表的头节点,头节点常常用来作为 链表的接入点)。图中另外一个值得注意的地方是,链表的尾元素指向一个 null 节点。
在上图中:我们说 bread 跟在 milk 后面,而不说 bread 是链表中的第二个元素。
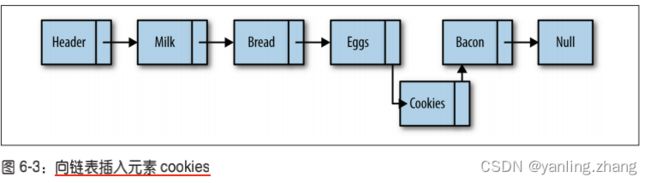
链表中插入一个节点的效率很高。向链表中插入一个节点,需要修改它前面的节点(前 驱),使其指向新加入的节点,而新加入的节点则指向原来前驱指向的节点。
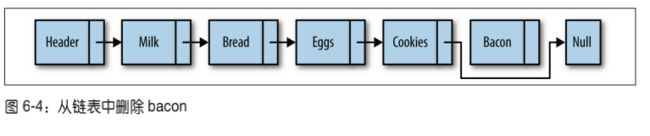
- 从链表中删除元素
从链表中删除一个元素也很简单。将待删除元素的前驱节点指向待删除元素的后继节点,同时 将待删除元素指向 null,元素就删除成功了。
设计一个基于对象的链表
思路:我们设计的链表包含两个类。Node 类用来表示节点,LinkedList 类提供了插入节点、删除 节点、显示列表元素的方法,以及其他一些辅助方法。
- Node 类
Node 类包含两个属性:
element 用来保存节点上的数据,next 用来保存指向下一个节点的 链接。
我们使用一个构造函数来创建节点,该构造函数设置了这两个属性的值:
function Node(element) {
this.element = element // 节点的数据
this.next = null // 指向下一个节点的链接
}
- LinkedList 类
LList 类提供了对链表进行操作的方法。该类的功能包括插入删除节点、在列表中查找给 定的值。该类也有一个构造函数,链表只有一个属性,那就是使用一个 Node 对象来保存该 链表的头节点。
function LList() {
this.head = new Node('head') // 链表的属性。 默认值为链表的头部节点。
// 链表的方法
this.find = find // 在列表中查找给 定的值
this.insert = insert // 插入新节点
this.remove = remove // 删除
this.display = display // 显示数据
this.findPrevious = findPrevious // 当前节点的前一个节点。
}
head 节点的 next 属性被初始化为 null,当有新元素插入时,next 会指向新的元素,所以 在这里我们没有修改 next 的值。
- 插入新节点
向链表中插入新节点 时,需要明确指出要在哪个节点前面或后面插入。
在一个已知节点后面插入元素时,先要找到“后面”的节点。为此,创建一个辅助方法 find(),该方法遍历链表,查找给定数据。如果找到数据,该方法就返回保存该数据的节 点。find的实现如下:
在链表中向后移动一位:currNode = currNode.next
function find(item) {
var currNode = this.head
// 开始循环链表。如果没找到就向后移动一位。
while(currNode.element !== item) {
currNode = currNode.next // 向后移动一位。继续寻找。
}
return currNode // 如果找到就返回
}
find() 方法演示了如何在链表上进行移动。首先,创建一个新节点,并将链表的头节点赋 给这个新创建的节点。然后在链表上进行循环,如果当前节点的 element 属性和我们要找 的信息不符,就从当前节点移动到下一个节点。如果查找成功,该方法返回包含该数据的 节点;否则,返回 null。
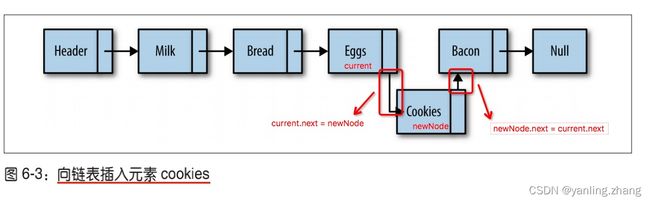
一旦找到“后面”的节点,就可以将新节点插入链表了。首先,将新节点的 next 属性设 置为“后面”节点的 next 属性对应的值。然后设置“后面”节点的 next 属性指向新节点。insert方法如下:
// newElement:新插入的元素
// item:在哪个元素 后面插入
function insert(newElement, item) {
var newNode = new Node(newElement) // 创建新插入节点的node
var current = this.find(item)
newNode.next = current.next
current.next = newNode
}
没插入任务数据时的链表:
element:是当前的值
next:指向下一个节点
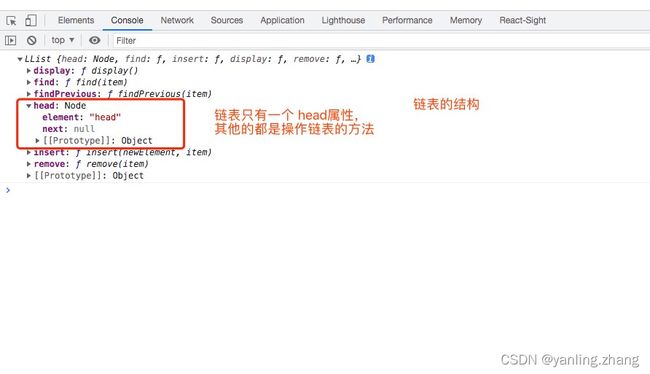
- 显示链表中的数据
function display() {
var currNode = this.head
while(!(currNode.next ==null)) {
console.log(currNode.next.element)
currNode = currNode.next
}
}
该方法先将列表的头节点赋给一个变量,然后循环遍历链表,当前节点的 next 属性为 null 时循环结束。为了只显示包含数据的节点(换句话说,不显示头节点),程序只访问 当前节点的下一个节点中保存的数据: currNode.next.element
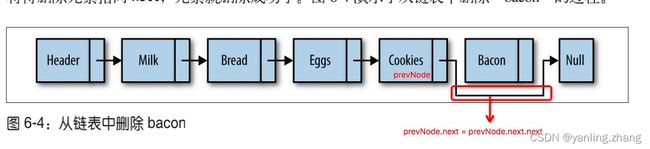
从链表中删除节点时,需要先找到待删除节点前面的节点。找到这个节点后,修改它的 next 属性,使其不再指向待删除节点,而是指向待删除节点的下一个节点。我们可以定义 一个方法 findPrevious(),来做这件事。该方法遍历链表中的元素,检查每一个节点的下 一个节点中是否存储着待删除数据。如果找到,返回该节点(即“前一个”节点),这样 就可以修改它的 next 属性了。
// 找到要删除节点的前一个节点
function findPrevious(item) {
var currNode = this.head
while(!(currNode.element === null) && (currNode.element !== item)) {
currNode = currNode.next
}
return currNode
}
function remove(item) {
var prevNode = this.findPrevious(item) // 被删节点的前一个节点
if (!(prevNode.next == null)) {
// prevNode.next:被删除节点的前一个节点的next
// prevNode.next.next:被删除节点的下一个next
prevNode.next = prevNode.next.next // 这里跳过了待删除节点,让“前一个”节点指向了待删除节点的后一个节点。
}
}
prevNode.next = prevNode.next.next 这里跳过了待删除节点,让“前一个”节点指向了待删除节点的后一个节点。
单向链表的完整代码
// Node节点
function Node(element) {
this.element = element // 节点的数据
this.next = null // 指向下一个节点的链接
}
// LList:链表的类
function LList() {
this.head = new Node('head')
this.find = find
this.insert = insert
this.display = display
this.remove = remove
this.findPrevious = findPrevious
// 查找一个指定节点
function find(item) {
var currNode = this.head;
while (currNode.element != item) {
currNode = currNode.next;
}
console.log('currNode', currNode)
return currNode;
}
/**
* 向链表中插入节点
*
* newElement:新插入数据
* item:插入到哪个节点后面
*/
function insert(newElement, item) {
var newNode = new Node(newElement); // 创建新插入节点的node
var current = this.find(item);
newNode.next = current.next;
current.next = newNode;
}
function display() {
var currNode = this.head
while(!(currNode.next ==null)) {
console.log(currNode.next.element)
currNode = currNode.next
}
}
/**
* findPrevious:找到当前节点的上一个节点
* item:当前节点
*/
function findPrevious(item) {
var currNode = this.head;
while (!(currNode.next == null) && (currNode.next.element != item)) {
currNode = currNode.next
}
console.log('delete', currNode)
return currNode
}
/**
* 删除一个节点
* item:被删除的节点
*/
function remove(item) {
var prevNode = this.findPrevious(item); // 找到要删除节点的前一个节点
console.log('prevNode.next', prevNode.next)
if(!(prevNode.next == null)) {
prevNode.next = prevNode.next.next
}
}
}
var cities = new LList()
cities.insert('conway', 'head')
cities.insert('liz', 'conway')
cities.insert('lucy', 'liz')
console.log(cities)
// console.log(cities.remove('conway'))
双向链表
尽管从链表的头节点遍历到尾节点很简单,但反过来,从后向前遍历则没那么简单。通过 给 Node 对象增加一个属性,该属性存储指向前驱节点的链接,这样就容易多了。此时向链 表插入一个节点需要更多的工作,我们需要指出该节点正确的前驱和后继。但是在从链表 中删除节点时,效率提高了,不需要再查找待删除节点的前驱节点了。
- 首当其冲的是要为 Node 类增加一个 previous 属性:
function Node(element) {
this.element = element
this.next = null
this.previous = null
}
- 双向链表的 insert() 方法和单向链表的类似,但是需要设置新节点的 previous 属性,使 其指向该节点的前驱。该方法的定义如下:
function insert(newElement, item) {
var newNode = new Node(newElement)
var current = this.find(item);
newNode.next = current.next
newNode.previous = current
current.next = newNode
}
- 双向链表的 remove() 方法比单向链表的效率更高,因为不需要再查找前驱节点了。首先需 要在链表中找出存储待删除数据的节点,然后设置该节点前驱的 next 属性,使其指向待删 除节点的后继;设置该节点后继的 previous 属性,使其指向待删除节点的前驱。
function remove(item) {
var current = this.find(item) // 被删除的节点
current.previous.next = current.next
current.next.previous = current.previous
current.next = null
current.previous = null
}
- 查找最后的节点 findLast
为了完成以反序显示链表中元素这类任务,需要给双向链表增加一个工具方法,用来查找 最后的节点。findLast() 方法找出了链表中的最后一个节点,同时免除了从前往后遍历链 表之苦:
// 查找链表中最后一个元素
function findLast() {
var currNode = this.head
while(!(currNode.next == null)) {
currNode = currNode.next
}
return currNode
}
- 反序显示双向链表中的元素 dispReverse
function dispReverse() {
var currNode = this.head;
currNode = this.findLast();
while(!(currNode.previous == null)) {
console.log(currNode.element)
currNode = currNode.previous
}
}
链表循环
循环链表和单向链表相似,节点类型都是一样的。唯一的区别是,在创建循环链表时,让 其头节点的 next 属性指向它本身。即:head.next = head。这种行为会传导至链表中的每个节点,使得每个节点的 next 属性都指向链表的头节点。换 句话说,链表的尾节点指向头节点,形成了一个循环链表。
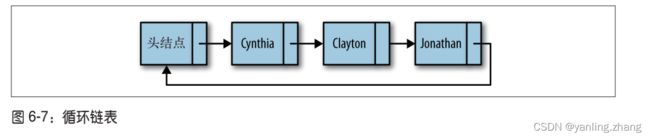
- 创建循环链表,只需要修改 LList 类的构造函数:
function LList() {
this.head = new Node('head')
this.head.next = this.head // 创建循环链表
this.find = find
this.insert = insert
this.display = display
this..findPrevious = findPrevious
this.remove = remove
}
- 只需要修改一处,就将单向链表变成了循环链表。但是其他一些方法需要修改才能工作正 常。
比如,display() 就需要修改,原来的方式在循环链表里会陷入死循环。while 循环的 循环条件需要修改,需要检查头节点,当循环到头节点时退出循环。
循环链表的 display() 方法
function display() {
var currNode = this.head
while(!(currNode.next == null) && !(currNode.next.element === 'head')) {
console.log((currNode.next.element)
currNode = currNode.next
}
}
六 字典
字典是一种以键 - 值对形式存储数据的数据结构。
字典(Dictionay) 类的基础是 Array 类,而不是 Object 类。
function Dictionay() {
this.dataSource = []
this.add = add
this.remove = remove
this.find= find
this.showAll = showAll
this.count = count // 字典中key的个数
this.clear = clear // 清空字典
// 接收2个参数:键:key,值:value
add(key,value) {
this.dataSource[key] = value
}
// key:键. 查找
find(key) {
return this.dataSource[key]
}
// 删除. key:键
remove(key) {
delete this.dataSource[key]
}
// 展示所有的键值对
showAll() {
for(var key in this.dataSource) {
console.log(key + '-->' this.dataSource[key])
}
}
//你可能想问:为什么不使用 length 属性?这是因为当键的类型为字符串时,
// length 属性 就不管用了。
count() {
var count = 0
for (var i = 0; i < this.datasouce.length; i++) {
++count
}
return count
}
// 清空字典
clear() {
for (var i = 0; i < this.datasouce.length; i++) {
delete this.datasouce[i]
}
}
}
七 散列
Map数据结构就是散列。
HashTable类
function HashTable() {
this.table = new Array(137)
this.simpleHash = simpleHash
this.showDistro = showDistro // 展示信息
this.put = put // 插入元素
this.get = get // 查询元素
}
八 集合
集合(set)是一种包含不同元素的数据结构。集合中的元素称为成员。集合的两个最重 要特性是:首先,集合中的成员是无序的;其次,集合中不允许相同成员存在。
集合是由一组无序但彼此之间又有一定相关性的成员构成的,每个成员在集合中只能出现 一次。在数学上,用大括号将一组成员括起来表示集合,比如{0,1,2,3,4,5,6,7,8,9}。集合 中成员的顺序是任意的,因此前面的集合也可以写做 {9,0,8,1,7,2,6,3,5,4},或者其他任意 形式的组合,但是必须保证每个成员只能出现一次。
• 不包含任何成员的集合称为空集,全集则是包含一切可能成员的集合。
• 如果两个集合的成员完全相同,则称两个集合相等。
• 如果一个集合中所有的成员都属于另外一个集合,则前一集合称为后一集合的子集。
对集合的操作:
1.并集: 将两个集合中的成员进行合并,得到一个新集合。
2.交集:两个集合中共同存在的成员组成一个新的集合。
3.补集:属于一个集合而不属于另一个集合的成员组成的集合。
Set类的实现
Set 类的实现基于数组,数组用来存储数据。
function Set(){
this.dataSource = []
this.add = add
this.remove = remove
this.size = size
this.union = union
this.interset = interset
this.subset = subset
this.difference = difference
this.show = show
// 添加元素:因为集合中不能包含相同的元素,所以,使用 add() 方法将数据存储到数组前,先要确保数 组中不存在该数据。
function add(data) {
if (this.dataSource.indexOf(data) < 0) {
this.dataSource.push(data)
return true
} else {
return false
}
}
function remove(data) {
var pos = this.dataSource.indexOf(data)
if (pos > 1) {
this.dataSource.splice(pos, 1)
return true
} else {
return false
}
}
function show() {
return this.dataSource
}
}
集合的更多操作
union() 方法执行并集操作,将 两个集合合并成一个。
该方法首先将第一个集合里的成员悉数加入一个临时集合,然后检 查第二个集合中的成员,看它们是否也同时属于第一个集合。如果属于,则跳过该成员, 否则就将该成员加入临时集合。
function contains(data) {
if (this.dataSource.indexOf(data) > -1) {
return true
} else {
return false
}
}
// 并集合
function union(set) {
var tempSet = new Set()
for(var i = 0; i < this.dataSource.length; i++) {
tempSet.add(this.dataSource[i])
}
for (var i = 0; i< set.dataSource.length; i++) {
const item = set.dataSource[i]
if (!tempSet.contains(item)) {
tempSet.dataSource.push(item)
}
}
return tempSet
}
// 交集
function intersect(set) {
var tempSet = new Set()
for (var i = 0; i < this.dataSource.length; i++) {
const item = this.dataSource[i]
if (set.contains(item)) {
tempSet.add(item)
}
}
return tempSet
}
function size() {
return this.dataSource.length
}
// 判断一个集合是否是另一个集合的子集。
/**
* subset() 方法首先要确定该集合的长度是否小于待比较 集合。
* 如果该集合比待比较集合还要大,那么该集合肯定不会是待比较集合的一个子集。
* 当该集合的长度小于待比较集合时,再判断该集合内的成员是否都属于待比较集合。
* 如果 有任意一个成员不属于待比较集合,则返回 false,程序终止。
* 如果一直比较完该集合的 最后一个元素,所有元素都属于待比较集合,
* 那么该集合就是待比较集合的一个子集,该 方法返回 true。
*/
function subset(set) {
console.log(this.size(), set.size())
if(this.size() > set.size()) {
return false
} else {
for (var i = 0; i < this.dataSource.length; i++) {
const menubar = this.dataSource[i]
if (!set.contains(menubar)) {
return false
}
}
return true
}
}
// difference: 求两个集合的补集
// 该方法返回一个新集合,该集合包含的是那些属于第一个 集合但不属于第二个集合的成员。
function difference(set) {
var tempSet = new Set();
for (var i = 0 ; i < this.dataSource.length; i++) {
const menubar = this.dataSource[i]
if (!set.contains(menubar)) {
tempSet.add(menubar)
}
}
return tempSet
}
测试
求两个集合的并集
var cis = new Set()
cis.add('liz')
cis.add('aimi')
cis.add('lucy')
var cis2 = new Set()
cis2.add('jack')
cis2.add('liz')
cis2.add('aimi')
// console.log(cis.dataSource, cis2.dataSource) // ['liz', 'aimi'] ['lucy', 'jack', 'liz']
// 并集
// console.log(cis.union(cis2).dataSource) // ['liz', 'aimi', 'lucy', 'jack']
// 交集
// console.log(cis.intersect(cis2).dataSource) // liz
// 判断一个集合是否是另一个集合的子集。
console.log(cis.subset(cis2))
// 求两个集合的补集
console.log(cis.difference(cis2).dataSource) // ['lucy']
九 二叉树和二叉查找树
树的定义
树被用来存储具有层级关系的数据,比如文件系统中的文件;树还被用来存储 有序列表。
选择树而不是那些基本的数据结构,是因 为在二叉树上进行查找非常快(而在链表上查找则不是这样),为二叉树添加或删除元素 也非常快(而对数组执行添加或删除操作则不是这样)。
树由一组以边连接的节点组成。公司的组织结构图就是一个树的例子

树的术语:
根节点: 一棵树最上面的节点称为 根节点
父节点:如果一个节点下面连接多个节点,那么该节点称为父节点,它下面的节点称为子 节点。
叶子节点:没有任何子节点的节点称为叶子节点。
从一个节点到另一个节点的这一组边称为路径。在图中用虚线表示。以某种特定顺序 访问树中所有的节点称为树的遍历。
二叉树是一种特殊的树,它的子节点个数不超过两个。二叉树具有一些特殊的计算性质, 使得在它们之上的一些操作异常高效。
树的深度:树的层数。
键:每个节点都有一个与之相关的值,该值有时被称为键。

二叉树和二叉查找树
二叉树:每个节点的子节点不允许超过两个。通过将子节点的个数限 定为 2,可以写出高效的程序在树中插入、查找和删除数据。
一个父 节点的两个子节点分别称为左节点和右节点。在一些二叉树的实现中,左节点包含一组特 定的值,右节点包含另一组特定的值。如下图的二叉树。
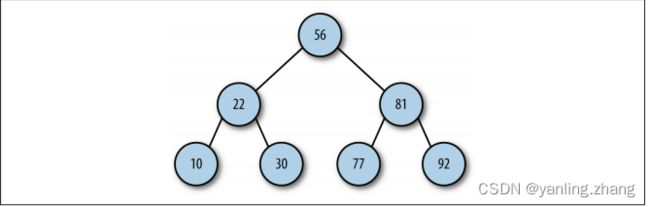
当考虑某种特殊的二叉树,比如二叉查找树时,确定子节点非常重要。
二叉查找树是一种 特殊的二叉树,相对较小的值保存在左节点中,较大的值保存在右节点中。这一特性使得 查找的效率很高。
实现二叉查找树:
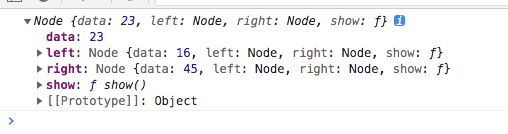
二叉查找树由节点组成,所以我们要定义的第一个对象就是 Node
// 节点信息
function Node(data, left, right) {
this.data = data
this.left = left
this.right = right
this.show = show
// 展示保存在节点中的数据
function show() {
return this.data
}
}
/*
现在可以创建一个类,用来表示二叉查找树(BST)。
我们让类只包含一个数据成员:一个 表示二叉查找树根节点的 Node 对象。该类的构造函数将根节点初始化为 null,以此创建 一个空节点。
*/
// 二叉查找树
function BST() {
this.root = null // 根节点
this.insert = insert // 插入一个节点
this.getMin = getMin // 查找最小值
this.getMax = getMax // 查找最大值
this.find = find // 查找给定的值
function insert(data) {
// 根据传入的data创建一个节点
var n = new Node(data, null, null)
// 如果没有根节点,就创建根节点
if (this.root === null) {
this.root = n
} else {
// 遍历二叉树
// 设置根节点为当前节点
var current = this.root
// debugger
var parent
while(true) {
parent = current
// 如果待插入节点保存的数据小于当前节点,则设新的当前节点为原节点的左节点;
if (data < current.data) {
current = current.left
// 如果当前节点的左节点为 null,就将新的节点插入这个位置,退出循环
if (current === null) {
parent.left = n
break;
}
} else {
// 设新的当前节点为原节点的右节点
current = current.right
// 如果当前节点的右节点为 null,就将新的节点插入这个位置,退出循环;
if (current === null) {
parent.right = n
break;
}
}
}
}
}
// 查找最小值 :
// 思路:因为较小的值总是在左子节点上,在 BST 上查 找最小值,只需要遍历左子树,直到找到最后一个节点。
// 该方法沿着 BST 的左子树挨个遍历,直到遍历到 BST 最左边的节点,该节点被定义为: current.left = null; 这时,当前节点上保存的值就是最小值。
function getMin() {
var current = this.root
while (!(current.left == null)) {
current = current.left
}
return current.data
}
// 查找最大值
// 思路:在 BST 上查找最大值,只需要遍历右子树,直到找到最后一个节点,该节点上保存的值即 为最大值。
function getMax() {
var current = this.root
while(!(current.right == null)) {
current = current.right
}
return current.data
}
// 如果找到给定值,该方法返回保存该值的节点;如果没找到,该方法返回 null。
function find(data) {
var current = this.root
while(current != null) {
if (current.data === data) {
return current.data
} else if (data < current.data) {
current = current.left
} else {
current = current.right
}
}
// 没找到返回null
return null
}
}
var nums = new BST()
nums.insert(23);
nums.insert(45);
nums.insert(99);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(22);
// 查看二叉二查找树的结构
console.log(nums.root)
// 获取最小值
var min = nums.getMin()
// console.log('min', min) // 3
// 获取最大值
var max = nums.getMax()
// console.log('max', max) // 99
// 查找某个值
var find = nums.find(2)
// console.log('find', find) // null
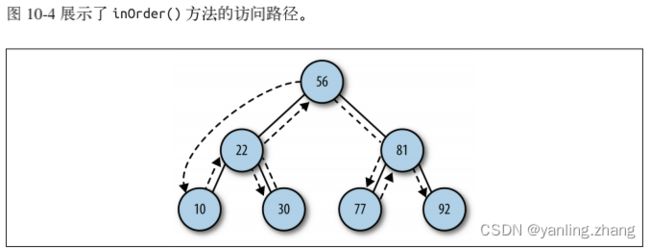
二叉查找树的遍历:
我们需要有能力遍历 BST,这样 就可以按照不同的顺序,比如按照数字大小或字母先后,显示节点上的数据。
有三种遍历 BST 的方式:中序、先序和后序。
中序遍历按照节点上的键值,以升序访问 BST 上的所有节点。先访问左子 树,再访问根节点,最后访问右子树。
先序遍历先访问根节点,然后以同样方式访问左子树和右子树。
后序 遍历先访问叶子节点,从左子树到右子树,再到根节点。
// 中序遍历
function inOrder(node) {
if (!(node == null)) {
inOrder(node.left)
console.log(node.show())
inOrder(node.right)
}
}
// 前序遍历
function prevOrder(node) {
if (!(node == null)) {
console.log(node.show())
prevOrder(node.left)
prevOrder(node.right)
}
}
// 后序遍历
function postOrder(node) {
if (!(node == null)) {
postOrder(node.left)
postOrder(node.right)
console.log(node.show())
}
}
// 中序遍历
inOrder(nums.root) // 3 16 22 23 37 45 99
// 先序遍历
prevOrder(nums.root) // 23 16 3 22 45 37 99
// 后序遍历
postOrder(nums.root) // 3 22 16 37 99 45 23
- 从二叉树上删除节点
从 BST 上删除节点的操作最复杂,其复杂程度取决于删除哪个节点。如果删除没有子节点 的节点,那么非常简单。如果节点只有一个子节点,不管是左子节点还是右子节点,就变 得稍微有点复杂了。删除包含两个子节点的节点最复杂。
为了管理删除操作的复杂度,我们使用递归操作,同时定义两个方法:remove() 和 removeNode()。
从 BST 中删除节点的第一步是判断当前节点是否包含待删除的数据,如果包含,则删除该 节点;如果不包含,则比较当前节点上的数据和待删除的数据。如果待删除数据小于当前 节点上的数据,则移至当前节点的左子节点继续比较;如果删除数据大于当前节点上的数 据,则移至当前节点的右子节点继续比较。
如果待删除节点是叶子节点(没有子节点的节点),那么只需要将从父节点指向它的链接 指向 null。
如果待删除节点只包含一个子节点,那么原本指向它的节点就得做些调整,使其指向它的 子节点。
最后,如果待删除节点包含两个子节点,正确的做法有两种:要么查找待删除节点左子树 上的最大值,要么查找其右子树上的最小值。这里我们选择后一种方式。
我们需要一个查找子树上最小值的方法,后面会用它找到的最小值创建一个临时节点。将 临时节点上的值复制到待删除节点,然后再删除临时节点。
function remove(data){
root = removeNode(this.root, data)
}
function removeNode(node, data) {
if (node == null) return null
if (data === node.data) {
// 没有子节点
if (node.left === null && node.right === null) return null
// 没有左子节点的节点
if (node.left === null) return node.right
// 没有右子节点的节点
if (node.right === null) return node.left
// 如果要删除的节点有2个节点
var tempNode = getSmallest(node.right)
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.left, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
- 计数