怒刷LeetCode的第25天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:闭合为环
第二题
题目来源
题目内容
解决方法
方法一:动态规划
方法二:组合数学
方法三:递归
方法四:数学公式
第三题
题目来源
题目内容
解决方法
方法一:动态规划
方法二:深度优先搜索(DFS)
第一题
题目来源
61. 旋转链表 - 力扣(LeetCode)
题目内容
解决方法
方法一:闭合为环
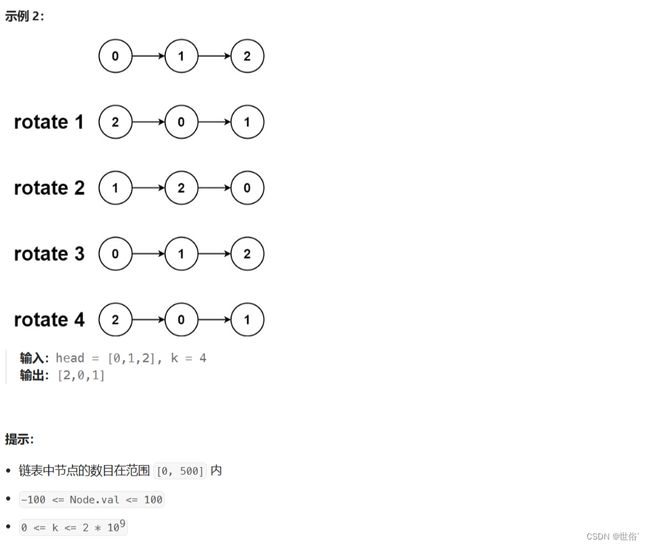
题目要求将链表中的节点向右移动 k 个位置,我们可以使用如下的思路来解决:
- 首先统计链表的长度,并将链表的尾节点与头节点相连,形成一个环状链表。
- 确定真正需要断开的位置,即倒数第 k+1 个节点(因为需要将第 k 个节点移动到头节点的位置)。
- 找到断开位置的前一个节点 pre,并将 pre 的 next 指针置为 null,这样链表就被切断成两部分。
- 将原本的尾节点指向原本的头节点,即完成了链表的旋转。
- 返回新的头节点。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode rotateRight(ListNode head, int k) {
// 处理特殊情况
if (head == null || head.next == null || k == 0) {
return head;
}
// 统计链表长度
int length = 1;
ListNode oldTail = head;
while (oldTail.next != null) {
length++;
oldTail = oldTail.next;
}
// 将链表的尾节点与头节点相连,形成环状链表
oldTail.next = head;
// 确定真正需要断开的位置
int newTailIndex = length - k % length - 1;
ListNode newTail = head;
for (int i = 0; i < newTailIndex; i++) {
newTail = newTail.next;
}
// 找到断开位置的前一个节点 pre
ListNode newHead = newTail.next;
newTail.next = null;
return newHead;
}
}复杂度分析:
- 时间复杂度:O(N),其中 N 表示链表的长度。我们需要先遍历链表求出链表的长度,然后再遍历链表找到新的尾节点并断开链表。总共需要遍历链表两次,因此时间复杂度是 O(N)。
- 空间复杂度:O(1),只需要常数的额外空间用于存储一些变量。
LeetCode运行结果:
第二题
题目来源
62. 不同路径 - 力扣(LeetCode)
题目内容
解决方法
方法一:动态规划
由于机器人只能向下或者向右移动一步,因此到达每个格子的路径只可能来自其上方格子或左侧格子。
设 dp[i][j] 表示从起点到 (i,j) 格子的路径数,则有:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
边界条件为 dp[0][j] 和 dp[i][0] 均为 1,因为对于第一行和第一列上的格子,机器人只能一直向右或向下走到终点。
最终答案即为 dp[m-1][n-1],也就是到达终点的路径总数。
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// 边界条件
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
// 状态转移
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}
复杂度分析:
时间复杂度:
- 初始化:需要填充边界条件,即 O(n + m) 的时间复杂度。
- 状态转移:需要遍历整个矩阵一次,对于每个格子需要常数时间进行计算,因此是 O(mn) 的时间复杂度。
因此总时间复杂度为 O(mn)。
空间复杂度:
使用了一个 m×n 的矩阵来存储中间状态,因此空间复杂度为 O(mn)。由于题目规定 m 和 n 都不超过 100,因此空间复杂度不会太大。
LeetCode运行结果:
方法二:组合数学
除了动态规划,还可以使用组合数学的方法来解决这个问题。
在一个 m×n 的网格中,机器人需要向下移动 m-1 步,向右移动 n-1 步,总共需要移动 m+n-2 步。在这些步骤中,机器人需要选择 m-1 个位置作为向下移动的步骤,并且剩下的 n-1 个位置作为向右移动的步骤。
因此,问题转化为从 m+n-2 个位置中选择 m-1 个位置的组合数。可以使用组合数公式来计算。
class Solution {
public int uniquePaths(int m, int n) {
// 计算组合数
long ans = 1;
for (int x = n, y = 1; y < m; ++x, ++y) {
ans = ans * x / y;
}
return (int) ans;
}
}
复杂度分析:
- 对于这种使用组合数公式计算路径数的方法,时间复杂度为 O(min(m, n))。这是因为在计算组合数时,需要进行 m-1 次乘法和除法运算,而 m-1 是较小的值。
- 空间复杂度是 O(1),因为只需要使用常数级别的额外空间来保存结果。
总结起来,这种方法相对于动态规划而言,在某些情况下可能更高效,尤其是当 m 和 n 较大时。但是需要注意的是,在 m 和 n 较接近时,两种方法的时间复杂度相差不大。
LeetCode运行结果:
方法三:递归
除了动态规划和组合数学,还可以使用递归来解决这个问题。
思路是从起点出发,每次向下或向右移动一步,并将问题转化为到达下一个格子的路径总数。递归的终止条件是到达终点时返回 1,表示找到一条有效路径。递归的过程中,将所有有效路径进行累加,并返回最终结果。
class Solution {
public int uniquePaths(int m, int n) {
return uniquePathsRecursive(m, n, 0, 0);
}
private int uniquePathsRecursive(int m, int n, int i, int j) {
// 到达终点,返回 1 表示找到一条有效路径
if (i == m - 1 && j == n - 1) {
return 1;
}
// 越界情况,返回 0 表示无效路径
if (i >= m || j >= n) {
return 0;
}
// 递归向下和向右移动一步,并将结果累加
return uniquePathsRecursive(m, n, i + 1, j) + uniquePathsRecursive(m, n, i, j + 1);
}
}
复杂度分析:
这种递归方法的时间复杂度较高,是指数级别的。因为在每个格子上,都会有两种选择:向下或向右移动。总共需要递归调用的次数为 2^(m+n-2),其中 m+n-2 是总共需要移动的步数。所以在 m 和 n 较大时,这种方法的效率会非常低。
因此,一般情况下推荐使用动态规划或组合数学的方法来解决路径计数问题。递归方法只在简单情况下使用,或者作为理解动态规划思想的一种辅助手段。
LeetCode运行结果:
方法四:数学公式
除了前面提到的动态规划、组合数学和递归方法外,还可以使用数学公式来计算路径数。
根据题目要求,机器人只能向下或向右移动,且每次只能移动一步。假设机器人需要从起点 (0, 0) 到达终点 (m-1, n-1),总共需要移动 m+n-2 步。
在这 m+n-2 步中,机器人必然需要选择 m-1 个位置作为向下移动的步骤,并且剩下的 n-1 个位置作为向右移动的步骤。
因此,问题可以转化为从 m+n-2 个位置中选择 m-1 个位置的组合数,即 C(m-1, m+n-2) 或 C(n-1, m+n-2)。
import java.math.BigInteger;
class Solution {
public int uniquePaths(int m, int n) {
BigInteger numerator = factorial(m + n - 2);
BigInteger denominator = factorial(m - 1).multiply(factorial(n - 1));
BigInteger paths = numerator.divide(denominator);
return paths.intValue();
}
// 计算阶乘
private BigInteger factorial(int n) {
BigInteger result = BigInteger.valueOf(1);
for (int i = 1; i <= n; i++) {
result = result.multiply(BigInteger.valueOf(i));
}
return result;
}
}
复杂度分析:
时间复杂度:
- 计算阶乘的复杂度为 O(m+n),其中 m 和 n 分别为矩阵的行数和列数。在计算阶乘时,需要进行 m+n-2 次乘法运算,每次乘法的时间复杂度为 O(1)。
- 除法运算的复杂度也为 O(m+n),其中 m 和 n 分别为矩阵的行数和列数。在进行除法运算时,需要对阶乘结果进行除法操作,每次除法的时间复杂度为 O(1)。
综合起来,使用数学公式来计算路径数的总体时间复杂度为 O(m+n)。
空间复杂度:
使用数学公式来计算路径数的空间复杂度为 O(1)。
在计算路径数时,只需要创建一个变量来保存阶乘的结果,并进行除法运算得到最终的路径数。因此,不需要额外的空间来存储中间结果或辅助数组,空间复杂度为常数级别的 O(1)。无论输入矩阵的大小如何,所需的额外空间都会保持不变。
需要注意的是,在实际应用中,计算阶乘可能会导致溢出问题。为了处理大数,可以使用大整数类来进行阶乘计算,例如 Java 中的 BigInteger 类。但是,由于大整数运算的效率较低,因此在 m 和 n 较大时,使用动态规划或其他更高效的方法会更合适。
LeetCode运行结果:
第三题
题目来源
63. 不同路径 II - 力扣(LeetCode)
题目内容
解决方法
方法一:动态规划
可以使用动态规划来解决这个问题。定义一个二维数组 dp,其中 dp[i][j] 表示从起始点到达网格位置 (i, j) 的不同路径数。
根据题目要求,如果某个网格位置有障碍物,则路径数为 0。对于其他位置,可以通过动态规划的递推关系求解。具体步骤如下:
1、初始化 dp 数组,将起始点的路径数设为 1。
2、遍历每个网格位置 (i, j),计算其路径数:
- 如果当前位置有障碍物,将 dp[i][j] 设为 0。
- 否则,dp[i][j] 可由其左侧位置 (i-1, j) 和上方位置 (i, j-1) 的路径数相加得到,即 dp[i][j] = dp[i-1][j] + dp[i][j-1]。
3、最后,返回终点位置 (m-1, n-1) 的路径数,即 dp[m-1][n-1]。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
// 初始化起始点路径数
dp[0][0] = obstacleGrid[0][0] == 0 ? 1 : 0;
// 计算路径数
for (int i = 1; i < m; i++) {
dp[i][0] = obstacleGrid[i][0] == 0 ? dp[i-1][0] : 0;
}
for (int j = 1; j < n; j++) {
dp[0][j] = obstacleGrid[0][j] == 0 ? dp[0][j-1] : 0;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
} else {
dp[i][j] = 0;
}
}
}
return dp[m-1][n-1];
}
}复杂度分析:
时间复杂度:O(mn),其中m 和n 分别是网格的行数和列数。需要遍历整个网格,对于每个网格位置最多只需要计算两次路径数,因此时间复杂度是O(mn)。
空间复杂度:O(mn),需要创建一个二维数组 dp 来记录每个网格位置的路径数。由于每个位置只与其上方和左侧的位置有关,因此需要使用一个与网格大小相同的二维数组,空间复杂度为 O(mn)。
LeetCode运行结果:
方法二:深度优先搜索(DFS)
从起始点开始递归遍历所有可能的路径,每次向下或向右移动一步。如果当前位置是障碍物或超出边界,则返回0;若已经到达终点,则返回1。通过累加向下和向右的路径数来计算不同的路径数。为了避免重复计算,可以使用记忆数组(memo)记录已经计算过的位置。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
return dfs(obstacleGrid, 0, 0, new int[m][n]);
}
private int dfs(int[][] obstacleGrid, int i, int j, int[][] memo) {
// 如果超出边界或遇到障碍物,返回0
if (i < 0 || j < 0 || i >= obstacleGrid.length || j >= obstacleGrid[0].length || obstacleGrid[i][j] == 1) {
return 0;
}
// 如果已经到达终点,返回1
if (i == obstacleGrid.length - 1 && j == obstacleGrid[0].length - 1) {
return 1;
}
// 如果当前位置已经计算过路径数,直接返回
if (memo[i][j] > 0) {
return memo[i][j];
}
// 向下和向右进行搜索,累加不同路径数
int paths = dfs(obstacleGrid, i + 1, j, memo) + dfs(obstacleGrid, i, j + 1, memo);
// 记录当前位置的路径数
memo[i][j] = paths;
return paths;
}
}
复杂度分析:
- 时间复杂度:O(m * n),需要遍历整个网格。
- 空间复杂度:O(m * n),需要使用记忆数组。
LeetCode运行结果: