ROC和AUC

目录

ROC

AUC

---

ROC

ROC曲线是Receiver Operating Characteristic Curve的简称，中文名为"受试者工作特征曲线"。ROC曲线的横坐标为假阳性率(False Postive Rate, FPR)；纵坐标为真阳性率(True Positive Rate, TPR).FPR和TPR的计算方法分别为

FPR= FP/N

TPR = TP/P

上式中，P是真实地正样本地数量，N是真实地负样本地数量，TP是P个正样本中被分类器预测为正样本地个数，FP是N个负样本中被分类器预测为正样本地个数。

如何绘制ROC曲线?

ROC曲线是通过不断移动分类器地"截断点"来生成曲线上地一组关键点地。

在二值分类问题中，模型地输出一般都是预测样本为正例地概率。样本按照预测概率从高到底排序。在输出最终地正例、负例之前，我们需要指定一个阈值，预测概率大于该阈值地样本会判为正例，小于该阈值则会被判为负例。比如，指定阈值为0.8，那么只有第一个样本会被预测为正例，其他全部都是负例。上面所说地“截断点”指的就是区分正负预测结果地阈值。

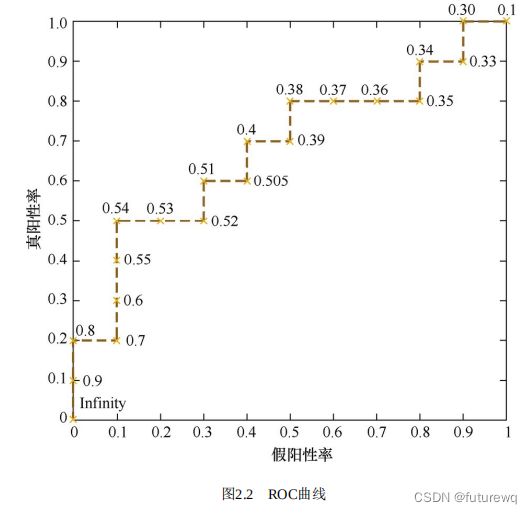
通过动态的调整截断点，从最高地得分开始，逐渐调整到最低得分，每一个截断点都会对应一个FPR和TPR，在ROC图上绘制出每个截断点对应地位置，再连接所有点就得到最终地ROC曲线。类似于下图

接下来用sklearn来实现。

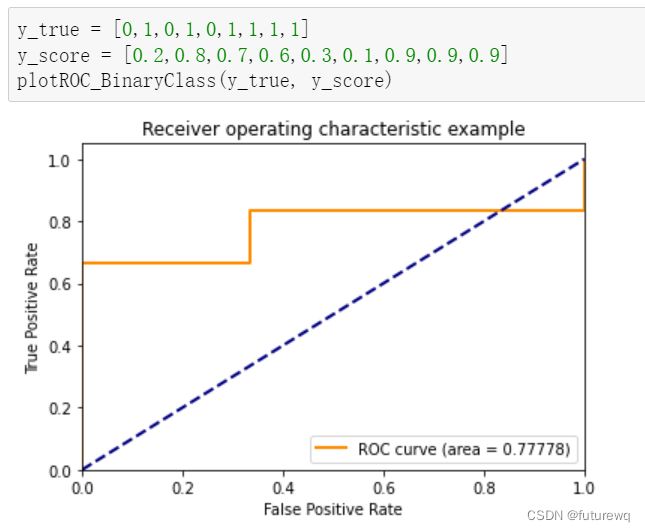
二分类的实现

def plotROC_BinaryClass(y_true, y_score0):
    '''
    :descript：绘制0-1类别的ROC曲线
    :param y_true: 真实标签，两个类别，[0,1]
    :param y_score: 预测值
    :return: ROC曲线
    '''
    from sklearn.metrics import roc_curve, auc
    from matplotlib import pyplot as plt
    
    fpr, tpr, thresholds = roc_curve(y_true,y_score0,pos_label=1)
    roc_auc = auc(fpr,tpr)
    
    plt.figure()
    lw = 2
    plt.plot(fpr, tpr, color='darkorange',
          lw=lw, label='ROC curve (area = %0.5f)' % roc_auc)
    plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('Receiver operating characteristic example')
    plt.legend(loc="lower right")
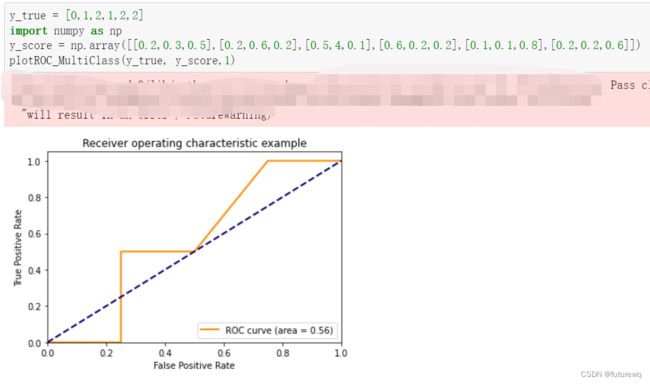
    plt.show()

 

多分类的实现(每个类分开处理即可)

def plotROC_MultiClass(y_true, y_score, class_num):
    '''
    :descript：绘制多类别的ROC曲线
    :param y_true: 真实标签，大于两个类别，[0,1,2]
    :param y_score: 预测值
    :return: ROC曲线
    '''
    from sklearn.metrics import roc_curve,auc
    from sklearn.preprocessing import label_binarize
    from matplotlib import pyplot as plt
    
    # 标签转换为one-hot
    classes = list(set(y_true))  # 类别
    n_classes = len(classes)  # 类别数
    y_true = label_binarize(y_true, classes)
#     y_score = label_binarize(y_score, classes)
    
    fpr = dict()
    tpr = dict()
    roc_auc = dict()
    for i in range(n_classes):
        fpr[i], tpr[i], _ = roc_curve(y_true[:,i],y_score[:,i],pos_label=1)
        roc_auc[i] = auc(fpr[i],tpr[i])
    
    plt.figure()
    # Plot of a ROC curve for a specific class
    plt.plot(fpr[class_num], tpr[class_num], color='darkorange',
             lw=2,label='ROC curve (area = %0.2f)' % roc_auc[class_num])  # 绘制类别one-hot中索引为2位置的类别ROC曲线
    plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('Receiver operating characteristic example')
    plt.legend(loc="lower right")
    plt.show()

 

AUC

AUC指的是ROC曲线下的面积大小，该值能够量化的反映基于ROC曲线衡量出的模型性能。

AUC的物理意义：正样本的预测结果大于负样本的预测结果的概率。所以AUC反映的是分类器对样本的排序能力。

插入一个重要问题。为什么说ROC和AUC都能应用于非均衡的分类问题？

ROC曲线只与横坐标(FPR)和纵坐标(TPR)有关系。我们可以发现TPR只是正样本中预测正确的概率，而FPR只是负样本中预测错误的概率，和正负样本的比例没有关系，因此ROC的值与实际的正负样本比例无关，因此既可以用于均衡问题，也可以用于非均衡问题。而AUC的几何意义为ROC曲线下的面积，因此也和实际的正负样本比例无关。

AUC的计算

• 法1：AUC为ROC曲线下的面积，那我们直接计算面积可得。面积为一个个小的梯形面积（曲线）之和。计算的精度与阈值的精度有关 。理论性质的，没法求解。
• 法2：根据AUC的物理意义，我们计算正样本预测结果大于负样本预测结果的概率。取n1* n0(n1为正样本数，n0为负样本数)个二元组，每个二元组比较正样本和负样本的预测结果，正样本预测结果高于负样本预测结果则为预测正确，预测正确的二元组占总二元组的比率就是最后得到的AUC。时间复杂度为O(N* M)。这个换种说法可能更利于我们后面的代码实现。首先，根据每个样本的预测概率值对真实标签进行倒序排序；然后，根据顺序，依次找到真实标签为1的样本，统计其后面样本概率值低于当前真实正样本的真实负样本的个数；最后，对所有值求和，再除以(正样本个数*负样本个数)
• 法3：我们首先把所有样本按照score排序，依次用rank表示他们，如最大score的样本，rank=n (n=n0+n1，其中n0为负样本个数，n1为正样本个数)，其次为n-1。那么对于正样本中rank最大的样本，rank_max，有n1-1个其他正样本比他score小,那么就有(rank_max-1)-(n1-1)个负样本比他score小。其次为(rank_second-1)-(n1-2)。最后我们得到正样本大于负样本的概率为 :

其计算复杂度为Ｏ(N+M) 。法3换种说法，有利于我们代码实现。首先，根据每个样本的预测概率对真实标签样本从小到大排序；然后，根据顺序，依次找到真实标签为1的样本，记录其(索引值+1)即上式中的rank，再按照上面的公式计算即可。

法2实现

def auc(y_true, y_pred):
    data = zip(y_true, y_pred)
    data = sorted(data, key=lambda x: x[1], reverse=True)
    data1 = [x[0] for x in data]
    true_posLabel = np.sum(y_true)
    true_negLabel = len(y_true) - true_posLabel
    count = 0
    for i in range(len(y_true)):
        if data[i][0] == 1:
            j = i+1
            while j < len(data) and data[j][1] >= data[i][1]:  # 这里直接忽略了概率相等时取0.5的情况
                j += 1
            count += (len(y_true) - j - np.sum(data1[j:]))
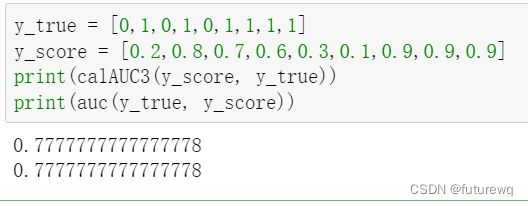
    return count/(true_negLabel * true_posLabel)

法3实现：

def calAUC3(y_pred, y_true):
	f = list(zip(y_pred.tolist(),y_true.tolist()))
	rank = [values2 for values1,values2 in sorted(f,key=lambda x:x[0])]
	rankList = [i+1 for i in range(len(rank)) if rank[i]==1]
	posNum = 0
	negNum = 0
	for i in range(len(y_true)):
		if(y_true[i]==1):
			posNum+=1
		else:
			negNum+=1
	auc = 0

	auc = float(sum(rankList)- (posNum*(posNum+1))/2)/(posNum*negNum)
	return auc  

 

 AUC和ROC是不平衡数据集中最常用的指标之一。

对于其他的评价指标需要时再整理把。

机器学习评估指标 - 知乎

机器学习评估与度量指标 - 知乎