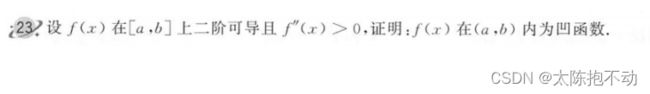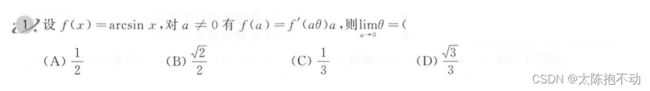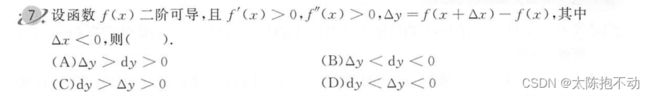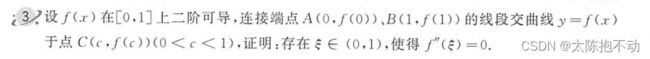- 情绪觉察日记第37天
露露_e800
今天是家庭关系规划师的第二阶最后一天,慧萍老师帮我做了个案,帮我处理了埋在心底好多年的一份恐惧,并给了我深深的力量!这几天出来学习,爸妈过来婆家帮我带小孩,妈妈出于爱帮我收拾东西,并跟我先生和婆婆产生矛盾,妈妈觉得他们没有照顾好我…。今晚回家见到妈妈,我很欣赏她并赞扬她,妈妈说今晚要跟我睡我说好,当我们俩躺在床上准备睡觉的时候,我握着妈妈的手对她说:妈妈这几天辛苦你了,你看你多利害把我们的家收拾得
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- 铭刻于星(四十二)
随风至
69夜晚,绍敏同学做完功课后,看了眼房外,没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深,都有些旧了,想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处,待到全部拆开后,又反复抚平纸张,然后仔细地一字字默看。只是开头的三个字是第一次看到,让她心漏跳了几拍。“亲爱的绍敏:从四年级的时候,我就喜欢你了,但是我一直不敢说,怕影响你学习。六年级的时候听说有人跟你表白,你接受了,我很难过,但
- UI学习——cell的复用和自定义cell
Magnetic_h
ui学习
目录cell的复用手动(非注册)自动(注册)自定义cellcell的复用在iOS开发中,单元格复用是一种提高表格(UITableView)和集合视图(UICollectionView)滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时,如果没有可复用的单元格,则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕,它就不会被销毁。相反,它被添
- 10月|愿你的青春不负梦想-读书笔记-01
Tracy的小书斋
本书的作者是俞敏洪,大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧,也是我事业上的偶像。本日摘录他书中第一章中的金句:『一个人如果什么目标都没有,就会浑浑噩噩,感觉生命中缺少能量。能给我们能量的,是对未来的期待。第一件事,我始终为了进步而努力。与其追寻全世界的骏马,不如种植丰美的草原,到时骏马自然会来。第二件事,我始终有阶段性的目标。什么东西能给我能量?答案是对未来的期待。』读到这里的时候,我便
- 学点心理知识,呵护孩子健康
静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所,超越教育与技术的思考》的讲座。今天又重新学习了一遍,收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题,她说心理健康的一些基本命题,我们与我们通常的一些教育命题是不同的,她还举了几个例子,让我们明白我们原来以为的健康并非心理学上的健康。比如如果
- 《投行人生》读书笔记
小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅,比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力,更多的是自我意识,你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议,细节,截止日期和数据很重要截止日期,一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
- ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
- 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
- 回溯 Leetcode 332 重新安排行程
mmaerd
Leetcode刷题学习记录leetcode算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets,其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。例如,行程[“JFK”,“LGA”]与[“JFK”,“LGB
- Python数据分析与可视化实战指南
William数据分析
pythonpython数据
在数据驱动的时代,Python因其简洁的语法、强大的库生态系统以及活跃的社区,成为了数据分析与可视化的首选语言。本文将通过一个详细的案例,带领大家学习如何使用Python进行数据分析,并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前,我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
- git常用命令笔记
咩酱-小羊
git笔记
###用习惯了idea总是不记得git的一些常见命令,需要用到的时候总是担心旁边站了人~~~记个笔记@_@,告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"
[email protected]"基本操作克隆远程仓库gitclone查看
- 2019-12-22-22:30
涓涓1016
今天是冬至,写下我的日更,是因为这两天的学习真的是能量的满满,让我看到了自己,未来另外一种可能性,也让我看到了这两年这几年的过程中我所接受那些痛苦的来源。一切的根源和痛苦都来自于人生,家庭,而你的原生家庭,你的爸爸和妈妈,是因为你这个灵魂在那一刻选择他们作为你的爸爸和妈妈来的,所以你得接受他,你得接纳他,他就是因为他的存在而给你的学习和成长带来这些痛苦,那其实是你必然要经历的这个过程,当你去接纳的
- 将cmd中命令输出保存为txt文本文件
落难Coder
Windowscmdwindow
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码,无可厚非,我们有必要保存我们的炼丹结果,但是复制命令行输出到txt是非常麻烦的,其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是:运行指令>输出到的文件名称或者具体保存路径测试下,我打开cmd并且ping一下百度:pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出:如果你再
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- 拥有断舍离的心态,过精简生活--《断舍离》读书笔记
爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多,虽然摆放整齐,但也时常会觉得空间逼仄,令人心生烦闷。抱着断舍离的态度,我开始阅读《断舍离》这本书,希望从书中能找到一些有效的方法,帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的,整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”,接着又成为每个人都能实行的“改变人生的断舍离”,从“哲学”逐渐升华成“
- 四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
- 高端密码学院笔记285
柚子_b4b4
高端幸福密码学院(高级班)幸福使者:李华第(598)期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲:刘莉一,知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫,目标永远下游。智者的梦再美,也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1,重视和珍惜的前提是知道它的价值非常重要,当你珍惜了,你就真正定下来,真正的学到身上。2,大家需要
- GitHub上克隆项目
bigbig猩猩
github
从GitHub上克隆项目是一个简单且直接的过程,它允许你将远程仓库中的项目复制到你的本地计算机上,以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南,帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前,你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统,用于跟踪和管理代码变更。你可以从Git的官方网站(https://git-scm.
- HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
- Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
- Day1笔记-Python简介&标识符和关键字&输入输出
~在杰难逃~
Pythonpython开发语言大数据数据分析数据挖掘
大家好,从今天开始呢,杰哥开展一个新的专栏,当然,数据分析部分也会不定时更新的,这个新的专栏主要是讲解一些Python的基础语法和知识,帮助0基础的小伙伴入门和学习Python,感兴趣的小伙伴可以开始认真学习啦!一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码,再通过语言处理程序执行向计算机发送指令,让计算机完成对应的工作,编程
- 人工智能时代,程序员如何保持核心竞争力?
jmoych
人工智能
随着AIGC(如chatgpt、midjourney、claude等)大语言模型接二连三的涌现,AI辅助编程工具日益普及,程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作,也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作,还是广泛学习以适应快速变化的技术环境?又或者,我们是否应该将重点转向AI无法轻易替代的软技能?让我们一起探讨程序员
- node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
- 阶段总结反思
轻争
马上就要进入10月份了,今天做一下前段时间的总结和反思。前段时间,日更、英语、健身、护肤坚持的比较好。阅读、书法坚持的不好。1.中间被迫停更半个多月,其余时间一直在坚持日更挑战。偶尔也有不想写的时候,就做一下摘抄。因为阅读(输入)没跟上来,所以写作(输出)质量有待进一步加强。2.英语做到了一周至少学习5天,每次不少于30分钟,但是小班课没有跟上更新速度,下一步要争取利用零碎时间补听小班课。3.减肥
- 数据仓库——维度表一致性
墨染丶eye
背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕,完整连接为:数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看,当一系列星型模型共享一组公共维度时,所涉及的维度称为一致性维度。当维度表存在不一致时,短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别,因为维度的差别,分析工作涉及的领域从简单到复杂,但是都是通过复杂的报表来弥补设计
- ARM驱动学习之基础小知识
JT灬新一
ARM嵌入式arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购(能不能买到,价格)–原理图(涉及到稳定性)•layout画板工程师–layout(封装、布局,布线,log)(涉及到稳定性)–焊接的一部分工作(调试阶段板子的焊接)•驱动工程师–驱动,原理图,layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案,原理图(网表)–layout工程师(gerber文件)–PCB板
- ARM驱动学习之5 LEDS驱动
JT灬新一
嵌入式C底层arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点:•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点:DRIVER_NAME和DEVICE_NAME匹配。实现步骤:1.加入需要的头文件://Linux平台的gpio头文件#include//三
- ARM驱动学习之4小结
JT灬新一
嵌入式C++arm开发学习linux
ARM驱动学习之4小结#include#include#include#include#include#defineDEVICE_NAME"hello_ctl123"MODULE_LICENSE("DualBSD/GPL");MODULE_AUTHOR("TOPEET");staticlonghello_ioctl(structfile*file,unsignedintcmd,unsignedlo
- 展现思维导图魅力,不断挖掘人生宝藏
思维导图讲师Mandy
第13期最强思维导图训练营已经结束一周了,但是我依旧是感觉所有学员还在努力的学习,这些学员中有教师、学生、白领、公务员、宝妈等等,只要你努力,只要你想改变自己,任何行业,任何岗位都可以参与进来,28天足以让你见成效,在这28天中,我们的学员不仅仅是收获了一枚毕业证,最重要的是让自己的思维方式得到升级,今天的你为自己投资,明天的你就会感谢你今天的付出,我们来听一听来自13期最强思维导图训练营优秀学员
- LeetCode[Math] - #66 Plus One
Cwind
javaLeetCode题解AlgorithmMath
原题链接:#66 Plus One
要求:
给定一个用数字数组表示的非负整数,如num1 = {1, 2, 3, 9}, num2 = {9, 9}等,给这个数加上1。
注意:
1. 数字的较高位存在数组的头上,即num1表示数字1239
2. 每一位(数组中的每个元素)的取值范围为0~9
难度:简单
分析:
题目比较简单,只须从数组
- JQuery中$.ajax()方法参数详解
AILIKES
JavaScriptjsonpjqueryAjaxjson
url: 要求为String类型的参数,(默认为当前页地址)发送请求的地址。
type: 要求为String类型的参数,请求方式(post或get)默认为get。注意其他http请求方法,例如put和 delete也可以使用,但仅部分浏览器支持。
timeout: 要求为Number类型的参数,设置请求超时时间(毫秒)。此设置将覆盖$.ajaxSetup()方法的全局
- JConsole & JVisualVM远程监视Webphere服务器JVM
Kai_Ge
JVisualVMJConsoleWebphere
JConsole是JDK里自带的一个工具,可以监测Java程序运行时所有对象的申请、释放等动作,将内存管理的所有信息进行统计、分析、可视化。我们可以根据这些信息判断程序是否有内存泄漏问题。
使用JConsole工具来分析WAS的JVM问题,需要进行相关的配置。
首先我们看WAS服务器端的配置.
1、登录was控制台https://10.4.119.18
- 自定义annotation
120153216
annotation
Java annotation 自定义注释@interface的用法 一、什么是注释
说起注释,得先提一提什么是元数据(metadata)。所谓元数据就是数据的数据。也就是说,元数据是描述数据的。就象数据表中的字段一样,每个字段描述了这个字段下的数据的含义。而J2SE5.0中提供的注释就是java源代码的元数据,也就是说注释是描述java源
- CentOS 5/6.X 使用 EPEL YUM源
2002wmj
centos
CentOS 6.X 安装使用EPEL YUM源1. 查看操作系统版本[root@node1 ~]# uname -a Linux node1.test.com 2.6.32-358.el6.x86_64 #1 SMP Fri Feb 22 00:31:26 UTC 2013 x86_64 x86_64 x86_64 GNU/Linux [root@node1 ~]#
- 在SQLSERVER中查找缺失和无用的索引SQL
357029540
SQL Server
--缺失的索引
SELECT avg_total_user_cost * avg_user_impact * ( user_scans + user_seeks ) AS PossibleImprovement ,
last_user_seek ,
- Spring3 MVC 笔记(二) —json+rest优化
7454103
Spring3 MVC
接上次的 spring mvc 注解的一些详细信息!
其实也是一些个人的学习笔记 呵呵!
- 替换“\”的时候报错Unexpected internal error near index 1 \ ^
adminjun
java“\替换”
发现还是有些东西没有刻子脑子里,,过段时间就没什么概念了,所以贴出来...以免再忘...
在拆分字符串时遇到通过 \ 来拆分,可是用所以想通过转义 \\ 来拆分的时候会报异常
public class Main {
/*
- POJ 1035 Spell checker(哈希表)
aijuans
暴力求解--哈希表
/*
题意:输入字典,然后输入单词,判断字典中是否出现过该单词,或者是否进行删除、添加、替换操作,如果是,则输出对应的字典中的单词
要求按照输入时候的排名输出
题解:建立两个哈希表。一个存储字典和输入字典中单词的排名,一个进行最后输出的判重
*/
#include <iostream>
//#define
using namespace std;
const int HASH =
- 通过原型实现javascript Array的去重、最大值和最小值
ayaoxinchao
JavaScriptarrayprototype
用原型函数(prototype)可以定义一些很方便的自定义函数,实现各种自定义功能。本次主要是实现了Array的去重、获取最大值和最小值。
实现代码如下:
<script type="text/javascript">
Array.prototype.unique = function() {
var a = {};
var le
- UIWebView实现https双向认证请求
bewithme
UIWebViewhttpsObjective-C
什么是HTTPS双向认证我已在先前的博文 ASIHTTPRequest实现https双向认证请求
中有讲述,不理解的读者可以先复习一下。本文是用UIWebView来实现对需要客户端证书验证的服务请求,网上有些文章中有涉及到此内容,但都只言片语,没有讲完全,更没有完整的代码,让人困扰不已。但是此知
- NoSQL数据库之Redis数据库管理(Redis高级应用之事务处理、持久化操作、pub_sub、虚拟内存)
bijian1013
redis数据库NoSQL
3.事务处理
Redis对事务的支持目前不比较简单。Redis只能保证一个client发起的事务中的命令可以连续的执行,而中间不会插入其他client的命令。当一个client在一个连接中发出multi命令时,这个连接会进入一个事务上下文,该连接后续的命令不会立即执行,而是先放到一个队列中,当执行exec命令时,redis会顺序的执行队列中
- 各数据库分页sql备忘
bingyingao
oraclesql分页
ORACLE
下面这个效率很低
SELECT * FROM ( SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_FS_RETURN order by id desc) A ) WHERE RN <20;
下面这个效率很高
SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_
- 【Scala七】Scala核心一:函数
bit1129
scala
1. 如果函数体只有一行代码,则可以不用写{},比如
def print(x: Int) = println(x)
一行上的多条语句用分号隔开,则只有第一句属于方法体,例如
def printWithValue(x: Int) : String= println(x); "ABC"
上面的代码报错,因为,printWithValue的方法
- 了解GHC的factorial编译过程
bookjovi
haskell
GHC相对其他主流语言的编译器或解释器还是比较复杂的,一部分原因是haskell本身的设计就不易于实现compiler,如lazy特性,static typed,类型推导等。
关于GHC的内部实现有篇文章说的挺好,这里,文中在RTS一节中详细说了haskell的concurrent实现,里面提到了green thread,如果熟悉Go语言的话就会发现,ghc的concurrent实现和Go有点类
- Java-Collections Framework学习与总结-LinkedHashMap
BrokenDreams
LinkedHashMap
前面总结了java.util.HashMap,了解了其内部由散列表实现,每个桶内是一个单向链表。那有没有双向链表的实现呢?双向链表的实现会具备什么特性呢?来看一下HashMap的一个子类——java.util.LinkedHashMap。
- 读《研磨设计模式》-代码笔记-抽象工厂模式-Abstract Factory
bylijinnan
abstract
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* Abstract Factory Pattern
* 抽象工厂模式的目的是:
* 通过在抽象工厂里面定义一组产品接口,方便地切换“产品簇”
* 这些接口是相关或者相依赖的
- 压暗面部高光
cherishLC
PS
方法一、压暗高光&重新着色
当皮肤很油又使用闪光灯时,很容易在面部形成高光区域。
下面讲一下我今天处理高光区域的心得:
皮肤可以分为纹理和色彩两个属性。其中纹理主要由亮度通道(Lab模式的L通道)决定,色彩则由a、b通道确定。
处理思路为在保持高光区域纹理的情况下,对高光区域着色。具体步骤为:降低高光区域的整体的亮度,再进行着色。
如果想简化步骤,可以只进行着色(参看下面的步骤1
- Java VisualVM监控远程JVM
crabdave
visualvm
Java VisualVM监控远程JVM
JDK1.6开始自带的VisualVM就是不错的监控工具.
这个工具就在JAVA_HOME\bin\目录下的jvisualvm.exe, 双击这个文件就能看到界面
通过JMX连接远程机器, 需要经过下面的配置:
1. 修改远程机器JDK配置文件 (我这里远程机器是linux).
- Saiku去掉登录模块
daizj
saiku登录olapBI
1、修改applicationContext-saiku-webapp.xml
<security:intercept-url pattern="/rest/**" access="IS_AUTHENTICATED_ANONYMOUSLY" />
<security:intercept-url pattern=&qu
- 浅析 Flex中的Focus
dsjt
htmlFlexFlash
关键字:focus、 setFocus、 IFocusManager、KeyboardEvent
焦点、设置焦点、获得焦点、键盘事件
一、无焦点的困扰——组件监听不到键盘事件
原因:只有获得焦点的组件(确切说是InteractiveObject)才能监听到键盘事件的目标阶段;键盘事件(flash.events.KeyboardEvent)参与冒泡阶段,所以焦点组件的父项(以及它爸
- Yii全局函数使用
dcj3sjt126com
yii
由于YII致力于完美的整合第三方库,它并没有定义任何全局函数。yii中的每一个应用都需要全类别和对象范围。例如,Yii::app()->user;Yii::app()->params['name'];等等。我们可以自行设定全局函数,使得代码看起来更加简洁易用。(原文地址)
我们可以保存在globals.php在protected目录下。然后,在入口脚本index.php的,我们包括在
- 设计模式之单例模式二(解决无序写入的问题)
come_for_dream
单例模式volatile乱序执行双重检验锁
在上篇文章中我们使用了双重检验锁的方式避免懒汉式单例模式下由于多线程造成的实例被多次创建的问题,但是因为由于JVM为了使得处理器内部的运算单元能充分利用,处理器可能会对输入代码进行乱序执行(Out Of Order Execute)优化,处理器会在计算之后将乱序执行的结果进行重组,保证该
- 程序员从初级到高级的蜕变
gcq511120594
框架工作PHPandroidhtml5
软件开发是一个奇怪的行业,市场远远供不应求。这是一个已经存在多年的问题,而且随着时间的流逝,愈演愈烈。
我们严重缺乏能够满足需求的人才。这个行业相当年轻。大多数软件项目是失败的。几乎所有的项目都会超出预算。我们解决问题的最佳指导方针可以归结为——“用一些通用方法去解决问题,当然这些方法常常不管用,于是,唯一能做的就是不断地尝试,逐个看看是否奏效”。
现在我们把淫浸代码时间超过3年的开发人员称为
- Reverse Linked List
hcx2013
list
Reverse a singly linked list.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
p
- Spring4.1新特性——数据库集成测试
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- C# Ajax上传图片同时生成微缩图(附Demo)
liyonghui160com
1.Ajax无刷新上传图片,详情请阅我的这篇文章。(jquery + c# ashx)
2.C#位图处理 System.Drawing。
3.最新demo支持IE7,IE8,Fir
- Java list三种遍历方法性能比较
pda158
java
从c/c++语言转向java开发,学习java语言list遍历的三种方法,顺便测试各种遍历方法的性能,测试方法为在ArrayList中插入1千万条记录,然后遍历ArrayList,发现了一个奇怪的现象,测试代码例如以下:
package com.hisense.tiger.list;
import java.util.ArrayList;
import java.util.Iterator;
- 300个涵盖IT各方面的免费资源(上)——商业与市场篇
shoothao
seo商业与市场IT资源免费资源
A.网站模板+logo+服务器主机+发票生成
HTML5 UP:响应式的HTML5和CSS3网站模板。
Bootswatch:免费的Bootstrap主题。
Templated:收集了845个免费的CSS和HTML5网站模板。
Wordpress.org|Wordpress.com:可免费创建你的新网站。
Strikingly:关注领域中免费无限的移动优
- localStorage、sessionStorage
uule
localStorage
W3School 例子
HTML5 提供了两种在客户端存储数据的新方法:
localStorage - 没有时间限制的数据存储
sessionStorage - 针对一个 session 的数据存储
之前,这些都是由 cookie 完成的。但是 cookie 不适合大量数据的存储,因为它们由每个对服务器的请求来传递,这使得 cookie 速度很慢而且效率也不