代码随想录01：【704.二分查找】【27.移除元素】

一.【704.二分查找】笔记

题目描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1

题目链接：力扣

文字讲解：代码随想录

视频讲解：手把手带你撕出正确的二分法 | 二分查找法 | 二分搜索法 | LeetCode：704. 二分查找_哔哩哔哩_bilibili

方法1：使用左闭右闭区间检索

解释：即在 [ left，right ] 这样的区间内检索目标值 target ，每次检索完成后更新区间的时候，要保证新区间的所有值，包括边界，都在检索的范围内

代码实现：

class Solution {
public:
    int search(vector& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;             //区别之处1 
        int middle = (left + right)/2;

        while(left <= right){                    //区别之处2
            middle = (left + right)/2;
            if(nums[middle] < target){
                left = middle + 1;               //区别之处3
            }
            else if(nums[middle] > target){
                right = middle - 1;
            }
            else{
                return middle;
            }
        }
        return -1;

    }
};

解析：

其实这个开闭区间最让人容易搞混的地方在于搜索的范围，这个搜索范围在比较大的时候还好，到区间比较小的时候就有点难想了，具体如下图

 也就是说如果在情况十分不理想时，直到最后才能搜索到target值，一般区间收缩到最后，它的长度都是一个一个的减小的，“4到3到2”或者“5到3到2”这样的，最后逃不过收缩到长度为2的区间

方法2：使用左闭右开区间检索

解释：即在 [ left，right ) 这样的区间内检索目标值 target ，每次检索完成后更新区间的时候，要保证新区间的左边界在检索的范围内，但是右边界不在检索范围内

代码：

class Solution {
public:
    int search(vector& nums, int target) {
        int left = 0;
        int right = nums.size();
        int middle = 0;

        while(left < right){
            middle = (left + right)/2;
            if(nums[middle] < target){
                left = middle + 1;
            }
            else if(nums[middle] > target){
                right = middle;
            }
            else{
                return middle;
            }
        }
        return -1;

    }
};

解析：

 也就是说如果在情况十分不理想时，直到最后才能搜索到target值，一般区间收缩到最后，它的长度的减小幅度受区间边界影响，如果是左边界收缩，那么区间长度是一个一个减小的；如果是右边界收缩，那么区间长度收缩的幅度大一些，最后可能一下子收缩到1；不过最后逃不过收缩到长度为1或者2的区间

---

二.【27.移除数组元素】笔记

题目描述：给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

        注1：不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组

        注2：元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素

题目链接：力扣

文字讲解：代码随想录

视频讲解：数组中移除元素并不容易！ | LeetCode：27. 移除元素_哔哩哔哩_bilibili

方法1：暴力求解

思路：使用两个for循环直接找到一个就删除一个，直到把所有的元素都遍历一遍

代码：

class Solution {
public:
    int removeElement(vector& nums, int val) {
        int length = nums.size();

        for(int i = 0; i < length;){
            if(nums[i] == val){
                for(int j = i; j < length - 1; j++){
                    nums[j] = nums[j + 1];
                }
                length--;                       //关键步骤
            }
            else{
                i++;                            //关键步骤
            }
        }

    return length;
    }
};

解析1：

                       、

因为这个原因，所以【i++】不能放在for循环的（）中，要单独找地方放，否则删除第一个2以后，i就指向元素4了，跳过了本该删除的第二个2

 解析2：

里层的for循环中【j < length - 1】，还是以上例子为例，把原本是4的位置填上5以后就该结束了，否则再往后进行复制，元素5所在的位置如果要赋值，那就要再往后取值，超过了数组的长度，所以报错

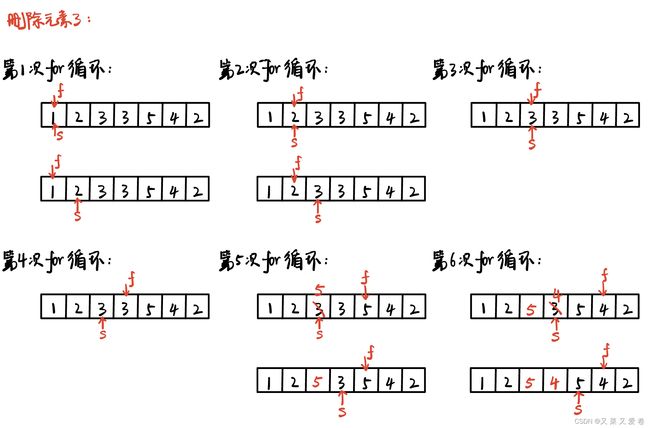
方法2：（同向）双指针法

思路：快指针 + 慢指针

        快指针：用来寻找新数组中所需要的元素

        慢指针：指向需要对原数组进行更新的位置

        注意1：当慢指针遇到第一个val元素的时候就停止了和快指针的同步移动，而且从这个慢指针指向位置开始往后所有的元素都需要被覆盖，无一例外

        注意2：其实在每次满足条件的 if 和 while循环 执行完后，慢指针都是领先于快指针一个身位的

代码：

lass Solution {
public:
    int removeElement(vector& nums, int val) {
        int length = nums.size();
        int slowIndex = 0;

        for(int fastIndex = 0; fastIndex <= length - 1; fastIndex++){
            if(nums[fastIndex] != val){
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }  
        }

    return slowIndex;
    }
};

//快指针：用来寻找新数组中所需要的元素
//慢指针：指向需要对原数组进行更新的位置
//
//注意：这里的双指针并不是真正的指针变量int*，而是两个int类型数据

解析：

方法3：（相向）双指针法

思路：左指针 + 右指针

        左指针：找左边等于 val 的值

        右指针：找右边不等于 val 的值

代码：

class Solution {
public:
    int removeElement(vector& nums, int val) {
        int leftIndex = 0;
        int rightIndex = nums.size() - 1;
        while (leftIndex <= rightIndex) {
            // 找左边等于val的元素
            while (leftIndex <= rightIndex && nums[leftIndex] != val){
                ++leftIndex;
            }
            // 找右边不等于val的元素
            while (leftIndex <= rightIndex && nums[rightIndex] == val) {
                -- rightIndex;
            }
            // 将右边不等于val的元素覆盖左边等于val的元素
            if (leftIndex < rightIndex) {
                nums[leftIndex++] = nums[rightIndex--];
            }
        }
        return leftIndex;   // leftIndex一定指向了最终数组末尾的下一个元素
    }
};

解析：

先让左边往前移动，再让右边往后移动，当两个指针都停下来的时候，进行值的覆盖

注意：覆盖完以后要同步更新左指针和右指针的指向，因为这个时候相当于从一个新的数组从头开始了，这个数组的范围是【left ， right】，left的左边和right的右边都是已经满足条件的数组值了，无需再动，关注这个新出现的子数组即可