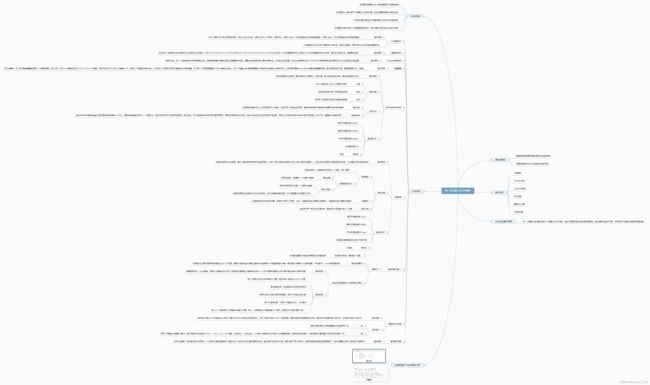
计算机算法设计与分析第二章思维导图&&知识点总结

复习链接

计算机算法设计与分析第一章思维导图
计算机算法设计与分析第二章思维导图&&知识点总结
计算机算法设计与分析第三章思维导图&&知识点总结
计算机算法设计与分析第四章思维导图&&知识点总结
计算机算法设计与分析第五章思维导图&&知识点总结 ( 初稿 )
计算机算法设计与分析第六章思维导图&&知识点总结 ( 初稿 )
计算机算法设计与分析第七章思维导图&&知识点总结 ( 初稿 )

思维导图

注：导图中的主定理模糊不清，可移步本文最下方观看清楚版。

递归的概念

直接或间接地调用自身的算法成为递归算法。
用函数自身给出定义的函数成为递归函数

递归实例

阶乘函数
Fibonacci数列
Ackerman函数
排列问题
整数划分问题
汉诺塔问题

分治法的基本思想

将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解决这些子问题，然后将各子问题合并得到原问题的解。

分治法特征：

1. 该问题的规模缩小到一定的程度就可以容易地解决
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

分治范例

二分搜索技术

基本思想：

将n个元素分成个数大致相同的两半，取a[n/2]与x作比较。如果x=a[n/2]，则找到x，算法终止；如果xa[n/2]，则只在数组a的右半部继续搜索x。
二分搜索技术充分利用了元素间的次序关系，采用分治策略，可最坏用$O(logn)$时间完成搜索任务。

大整数的乘法

基本思想：

将n位的X,Y各自都分成2段，每段长n/2位(假设n为2的幂次)，即$X=A\ast 10^{n/2}+B$，$Y=C\ast 10^{n/2}+D$，则$XY=AC\ast 10^n+10^{n/2}\ast ((A-B)\ast (D-C)+AC+BD)+BD$。即一次n位的整数乘法可以化简为三次n/2位的整数乘法与6次减法。通过减少乘法次数，提高算法效率。

Strassen矩阵乘法

基本思想：

使用分治法，将一个矩阵转换为子矩阵相乘的方式。矩阵乘法耗费时间要比矩阵加法耗费的时间多，想要改进矩阵乘法的计算时间复杂性，必须减少乘法运算。Strassen矩阵乘法用了7次对于n/2阶矩阵乘积的递归调用和18次n/2阶矩阵的加减运算。

棋盘覆盖

基本思想：

用分治策略，可以设计解棋盘覆盖问题的一个简捷的算法。当k>0时，将$2^k\ast 2^k$棋盘分割为4个$2^{k-1}\ast 2^{k-1}$子棋盘。特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割，直至棋盘简化为$1\ast 1$棋盘。

合并排序

基本思想：

合并排序是用分治思想，首先将序列分为两部分，然后对每一部分进行递归的排序，最后将结果进行合并。

具体步骤：

（1）分解：将n个元素分成个含n/2个元素的子序列。
（2）解决：用合并排序法对两个子序列递归排序。
（3）合并：合并两个已排序的子序列已得到排序结果。

实现方式：

递归版本：

将待排序元素分成大小大致相同的两个子集合，分别对两个子集合进行排序，最终将排好序的子集合合并成要求的排好序的集合。

非递归版本：

递归版本的合并算法的递归过程只是将待排序集合一分为二，直至待排序集合只剩下一个元素为止，然后不断合并两个排好序的数组段。按此机制，可以先将数组中的相邻两元素两两配对，再用合并算法将它们排序，构成n/2组长度为2的排好序的子数组段，再将它们排序成长度为4的排好序的字数组段。如此下去，直至整个数组排好序。

复杂度分析：

最坏时间复杂度：$O(nlogn)$
最好时间复杂度：$O(nlogn)$
平均时间复杂度：$O(nlogn)$
空间复杂度：$O(n)$
稳定性：稳定

快速排序

基本思想：

快速排序使用分治的思想，通过一趟排序将待排序列分割成两部分，其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序，以达到整个序列有序的目的。

具体步骤：

(1)选择基准：在待排序列中，按照某种方式挑出一个元素，作为 “基准”（pivot）
(2)分割操作：以该基准在序列中的实际位置，把序列分成两个子序列。此时，在基准左边的元素都比该基准小，在基准右边的元素都比基准大
(3)递归处理：递归地对两个序列进行快速排序，直到序列为空或者只有一个元素。

选择基准的方式：

（1）固定位置
取序列的第一个或最后一个元素作为基准
（2）随机化选择
随机取待排序列中任意一个元素作为基准
快速排序算法的性能取决于划分的对称性。而划分基准的随机选择，可以使期望划分变得较为对称。

复杂度分析：

最坏时间复杂度：$O(n^2)$
最好时间复杂度：$O(nlogn)$
平均时间复杂度：$O(nlogn)$
空间复杂度：根据实现方式的不同而不同
稳定性：不稳定

选择问题求第k小

（1）先排序(非降序)，再取第k个元素。

时间复杂度等于所选的排序算法的时间复杂度

（2）随机选择算法

利用随机划分算法思想将原问题划分为2个子问题，根据子问题所包含元素的位置来决定选择哪个子问题继续递归求解。最坏情况下需要O(n^2)得到答案，平均情况下，O(n)可得问题的解。

（3）线性时间选择算法(又称顺序统计算法)

算法思想：

如果能够找到一个划分基准，使得这个基准的划分的两个子数组的长度都至少是原来的$\epsilon$倍（0 < $\epsilon$ < 1），则子问题的规模为$\epsilon n$，那么最坏情况也能O（ n )解决问题。

算法步骤：

将n个元素划分成$\lceil n/5\rceil$组，每组5个元素，至多只有一组包含n mod 5个元素
通过每组排序，找出每组的中位数构成序列M
取序列M的中位数x(若序列有偶数，取两个中位数中较大者)
用x作为基准元素，对原n个元素进行划分，i为分裂点
若k<=j，则用前部分子问题递归求第k小元素；
若k>j，则用后部分子问题求第k-i小元素
j为前部分子问题元素的个数。

最接近点对问题

基本思想：

将所给的平面上n个点的集合S分为两个子集S1和S2(可以按照x坐标排序中分)，每个子集中约有n/2个点，然后在每个子集中递归地求其最接近的点对。最近点对可能单纯在S1或S2中，也可能分别在S1和S2中。对于这个问题，
一维：第三种情况只可能是最靠近中线的那两个点。
二维：取两个子集递归求解最小值为d，第三种情况只会发生在 ( mid - d , mid + d ) 内，这个范围，mid左边p1，mid右边p2，p1中每个点最多在p2中存在6个点会更新答案，即按照y坐标排序后，p1每点最多只要检查p2中排好序的相继6个点。

循环赛日程表

基本思想：

采用分治策略，将所有的选手分成两半，n个选手的比赛日程表就可以通过为n/2个选手设计的比赛日程表来决定。递归地用对选手进行分割，直到只剩下两个选手时，比赛日程表的制定就变得很简单了。这时只需要让这两个选手进行比赛即可。

主定理-基于分治的算法分析

简化版：

对于递推式$T(n)=aT(\frac{n}{b})+\Theta (n^d)$，其中 d >= 0 ，那么：

$T(n)=\{\begin{array}{ll}\Theta (n^d)，& 当a<b^d\\ \Theta (n^{d}logn)，& 当a=b^d\\ \Theta (n^{lo{g}_{b}a})，& 当a>b^d\end{array}$

完整版：

深入学习