机器学习-使用决策树DecisionTreeRegressor模型对水果蔬菜价格预测
决策树-常用于数据分析领域的分类和回归
数据集fruitvegprices-2017_2022.csv数据集来对水果价格的预测。
水果蔬菜价格数据集自取
本数据用来学习所用,如有错误请指正
决策树
首先我们了解到决策树 [Decision Tree]可以用来解决什么样的问题?
分类
回归
对于不同的数据选择不同的方法,分类问题的数据集主要表现为离散型,区间不可分等情况,简单来说就是预测真与假,例如在scikit-learn中Datas数据库中的iris数据集,可用通过决策树来预测-是鸢尾-非鸢尾。回归问题的数据集主要表现为连续型,区间可分等情况,此次对水果蔬菜价格分析则是利用到了回归问题,利用均方误差来作为当前节点分裂标准。
决策数的构造
首先确定根节点的选择,这是一颗树开始分裂的标准。通过entropy这一概念来介绍一颗数的构成。我们通过一个简单的例子来说明,
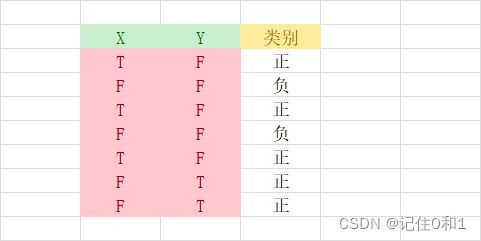
我们假设某类物体 X Y 有两种状态 T F ,现在我们通过对上述计算来选择第一个要分裂的点,也就是特征选择作为依次从上到下构建树的标准。熵是以二进制位的个数来度量编码长度,对数的底数为2,对于目标属性X[5+,2-],这样可以计算出系统的熵(这里的熵是针对布尔类型)计算分类后的熵,也就是计算对于X类别,来计算类别X下T的[3+,0-],F[2+,2-],依次来得出Y类别下的T F。接下来计算X属性相对于目标属性下的信息增益Gani(S,X),也就是用原集合的熵减去X分类值后的期望值,依次来计算出Y类别下的。我们通过信息增益大的来作为第一个根节点。
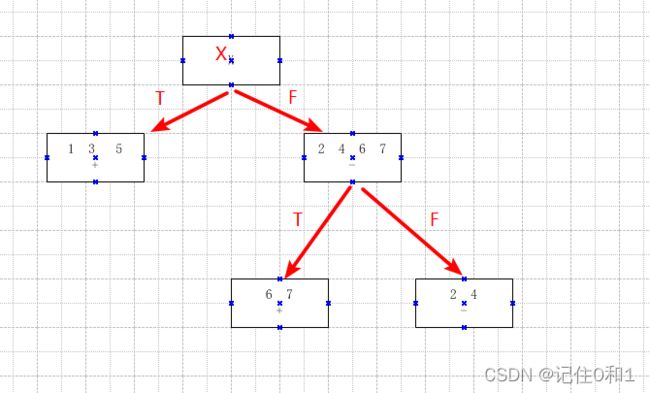
选取信息增益最大X作为根节点,此问题为简答的分类问题,以此来对决策树的了解。
回归正题
1.明确数据集是用来做什么的
2.数据的处理
3.特征工程
4.利用决策树进行数据预测
数据集
fruitvegprices-2017_2022.csv
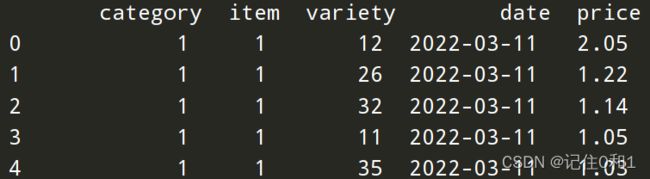
1.1对数据进行基础分析
![]()
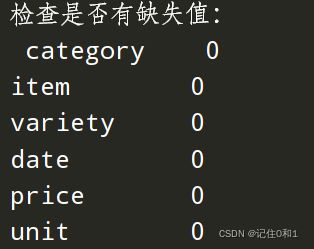
数据的缺失会造成分析结果的不准确,假如数据中包含空值,可能最后会的得到预测值的不准确。
对缺失值的处理,可以分为丢弃,补全。当缺失值占比很大时可以选择删除,对于补全缺失值可以选择 插值填充 均值填充等,具体数据要具体分析。
```python
'行列信息:',data.shape#检查形状
'检查唯一值:',data.nunique#检查唯一值
'检查是否有缺失值:\n',data.isnull().sum()#检查是否有缺失值
data.info()
data.head(10)
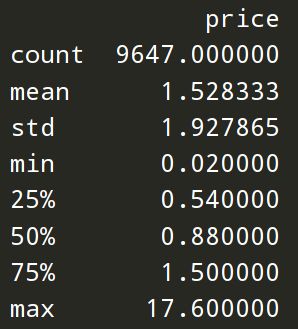
data.price.describe()
1.1 数据集预处理
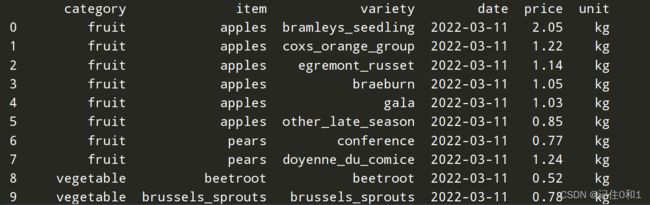
通过观察到unit是单位,对数据集的影响很小,删除不相关且数据集没有影响的特征。
1.1.1 [‘category’,‘item’,‘variety’]
1.1.2 [date]
日期类型要进行分割处理
这两部分的预处理
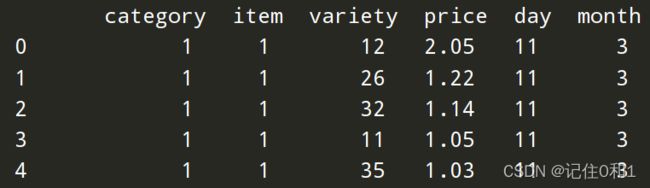
标准化 归一化
通过观察可以发现 【item】,【variety】这两类再转为数字类型时,数值过大在训练预测时 会导致预测价格准确性。
在这依次给出两种方式:标准化,归一化。
1.2 标准化
对原始数据进行变换把数据变换到均值为0,标准差为1的范围内。
X=(x-mean)/var*0.5
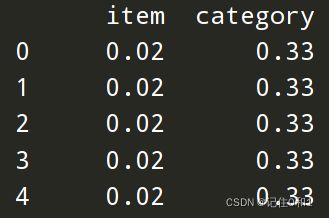
标准化后数据(针对[‘item’]):
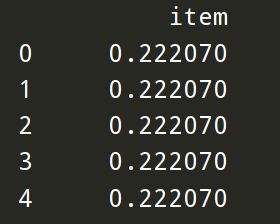
def unitize(dataset):
'''
unitize:
标准化特征值
return:
标准化后的数据集 normalization
'''
m = dataset.shape[0]
x = 0
mean = np.mean(dataset,axis=0)
n = np.tile(mean,(m,1))
normalization = pd.DataFrame(dataset) - n
for i in list(dataset):
x+=1
std = pow((pd.DataFrame(dataset) - np.tile(mean,(m,1)))**2 / x,0.5)
normalization = normalization / std
return normalization
1.3 归一化
对原始数据进行变换把数据映射到【0,1】之间。
X=(x-min)/(max-min)
def Stand(dataset):
"""
Stand:
归一化特征值
return:
归一化后的数据集 Dataset
"""
#准备数据 max min man_min
mindata = dataset.min(0)
maxdata = dataset.max(0)
max_min = maxdata-mindata
m = dataset.shape[0]
Dataset = np.zeros(np.shape(dataset))
n = np.tile(mindata,(m,1)) #组成最小值得矩阵
Dataset = pd.DataFrame(dataset) - n
Dataset = Dataset / np.tile(max_min, (m, 1))
return Dataset
1.4 特征工程
对数据进行分割 以4:1的比例来划分出训练集和测试集
x=pd.concat([data.drop(['price','item','variety'],axis=1),item_category],axis=1)
y = data['price']
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=0)
scikit-learn 决策树API
scikit-learn的DecisionTreeRegressor 中的特征选择选择是均方误差,也可以选择前面提到的“entropy”,也可以是“gini”,”mae“。
均方误差(mse): 评判数据的变化程度,估计值与真实值之差平方的期望。
模型中默认“best” 即在在特征的所有划分点中找出最优的划分点
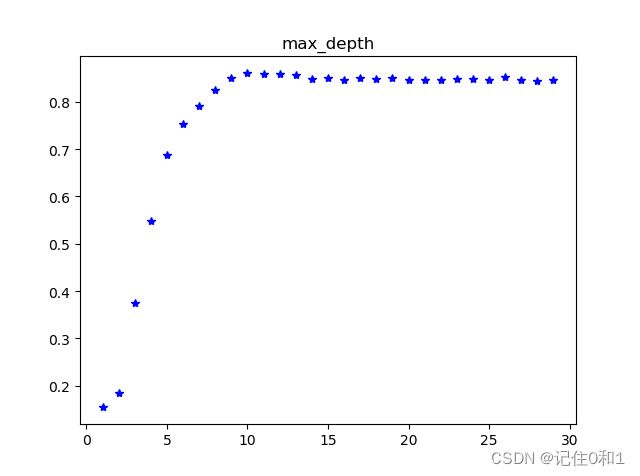
最大深度(max_depth):决策树建立时需要限制输的深度来防止出现过拟合,也可以通过max_leaf_nodes来限制
def __init__(
self,
*,
criterion="squared_error",
splitter="best",
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
ccp_alpha=0.0,):
对于一些参数的调整, 选择使用网格搜索GridSearchCV 为模型找到最佳参数 max_depth min_samples_split min_samples_leaf
#对深度进行交叉验证
depth = list(range(1,30))
param_grid = dict(max_depth=depth)
tree = GridSearchCV(DecisionTreeRegressor(),param_grid,cv=10,refit=True)
tree.fit(x_train,y_train)
print("Best parameter:",tree.best_params_,
"\nBest Estimator:",tree.best_estimator_,
"\nBest Score:",tree.best_score_)
1.5 通拟合优度来评判模型训练
拟合优度是指回归直线对观测值的拟合程度
R^2→1,模型的数据拟合性就越好
R^2→0,模型的数据拟合度越差
如果在测试集和训练集上拟合优度差值较大,则模型在一定程度上过拟合
dt_train_pred = dtr.predict(x_train)
dt_test_pred = dtr.predict(x_test)
print("测试集:",r2_score(y_test,dt_test_pred))
print("训练集:",r2_score(y_train,dt_train_pred))
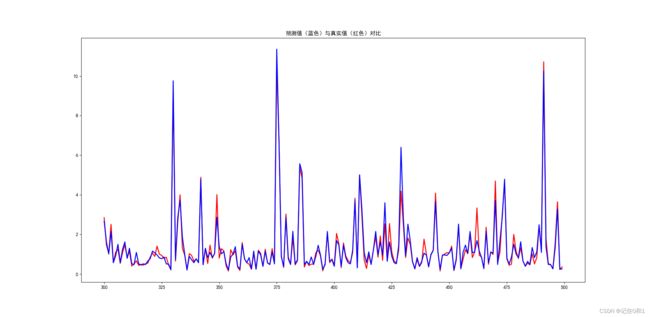
1.6 预测与真实可视化
x_data = y_test[300:500]
y_data = dt_test_pred[300:500]
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['font.serif'] = ['SimHei'] # 设置正常显示中文
plt.title('预测值(蓝色)与真实值(红色)对比')
plt.plot(x_data,color='red',linewidth=2,linestyle='-')
plt.plot(y_data,color='blue',linewidth=2,linestyle='-')
plt.show()
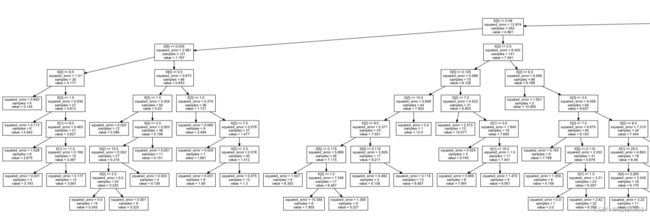
1.7 以均方误差为节点的可视化树
joblib.dump(dtr,"./f_V.pkl")
dot_data = tree.export_graphviz(dtr,out_file=None)
graph = graphviz.Source(dot_data)
graph.render("tree")
1.8 核心代码如下
def getLabel_date(DataPath):
'''
对标签,日期进行处理
:return: 处理好的数据data
'''
data = pd.read_csv(DataPath)
code = LabelEncoder()
labels = ['category','item','variety']
for label in labels:
data[label] = code.fit_transform(data[label]).astype(int)
data = data.drop(['unit'],axis=1)
# print("标签处理:\n",data.head(20))
# data['no_of_zeros']=(data == 0).astype(int).sum(axis=1)
# data=data[data['no_of_zeros'] <1].drop(['no_of_zeros'], axis=1)
data['date'] = pd.to_datetime(data['date'])
data['day'] = data['date'].dt.day
data['month'] = data['date'].dt.month
data['year'] = data['date'].dt.year
data = data.drop(['date'],axis=1)
y = data['year']
n = data['year'].shape[0]
data['year'] = -(pd.DataFrame(y) - np.tile(2022,(n,1)))
return data
def Standdata(data):
'''
data: 对连续的标签数据进行归一化,对归一化的数据保留两位小数便于分析
:return: item variety
'''
item = Stand(data['item'])
item = round(item,2)
variety = Stand(data['variety'])
variety = round(variety,2)
item_variety = pd.concat([item,variety],axis=1)
# print("item_variety:\n",item_variety.head(20))
return item_variety
def TrainAndTest(data,item_variety):
'''
分割出测试集 训练集
:return: 四个数据
'''
x = pd.concat([data.drop(['price','item','variety',],axis=1),item_variety],axis=1)
y = data['price']
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=0)
return x_train,x_test,y_train,y_test
def TreeRegressor(x_train,y_train):
'''
利用网格搜索交叉验证进行调参 防止过拟合
:return: 调参后的数据重新防数回归树中进行测试
'''
depth = list(range(1,30))
param_grid = dict(max_depth=depth)
tree = GridSearchCV(DecisionTreeRegressor(),param_grid,cv=10,refit=True)
tree.fit(x_train,y_train)
means = tree.cv_results_['mean_test_score']
params = tree.cv_results_['params']
for mean,param in zip(means,params):
for depth in param:
# print("%f-:%r" % (mean,param[depth]))
mean_param = list([mean,param[depth]])
plt.plot(mean_param[1],mean_param[0],'b*')
plt.title('max_depth')
plt.show()
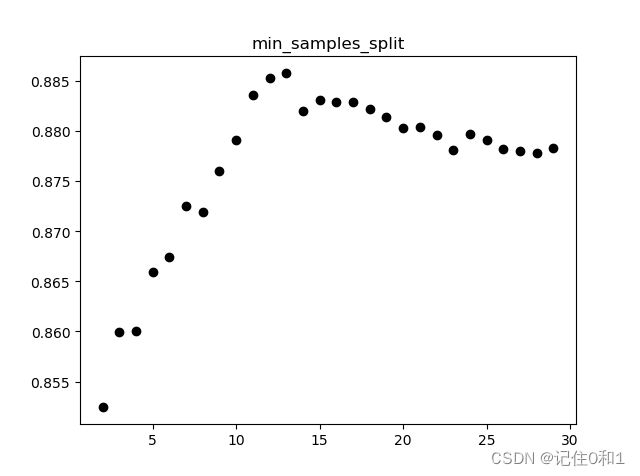
depth = list(range(2,30))
param_split = dict(min_samples_split=depth)
tree = GridSearchCV(DecisionTreeRegressor(max_depth=10),param_split,cv=5,refit=True)
tree.fit(x_train,y_train)
means = tree.cv_results_['mean_test_score']
params = tree.cv_results_['params']
for mean,param in zip(means,params):
for depth in param:
mean_param = list([mean,param[depth]])
plt.plot(mean_param[1],mean_param[0],'ko')
plt.title('min_samples_split')
print('最终交叉验证完后:',tree.score(x_test,y_test))
print("每个超参数每次交叉验证得结果:",tree.cv_results_)
plt.show()
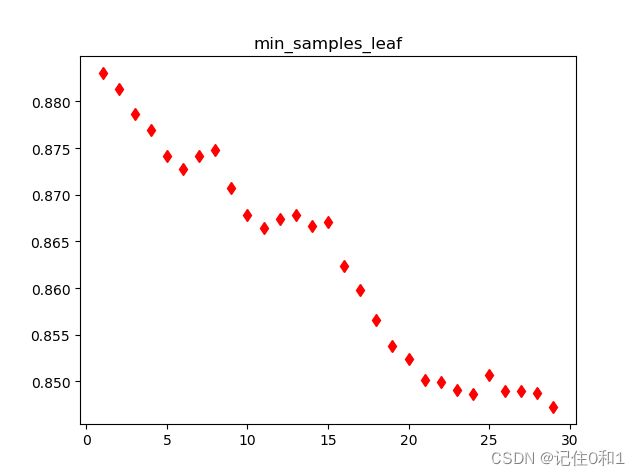
samples_split = list(range(1,30))
param_leaf = dict(min_samples_leaf=samples_split)
tree = GridSearchCV(DecisionTreeRegressor(max_depth=10,min_samples_split=15),param_leaf,cv=5,refit=True)
tree.fit(x_train,y_train)
means = tree.cv_results_['mean_test_score']
params = tree.cv_results_['params']
for mean,param in zip(means,params):
for depth in param:
mean_param = list([mean,param[depth]])
plt.plot(mean_param[1],mean_param[0],'rd')
plt.title('min_samples_leaf')
plt.show()
print("Best parameter:",tree.best_params_,
"\nBest Score:",tree.best_score_)
dtr = DecisionTreeRegressor(criterion='squared_error',max_depth=10,min_samples_split=15,min_samples_leaf=1)
dtr.fit(x_train,y_train)
return dtr
def r2score_score(dtr,x_train,x_test,y_train,y_test):
dt_train_pred = dtr.predict(x_train)
dt_test_pred = dtr.predict(x_test)
print("测试集:{:1f}".format(r2score(y_test,dt_test_pred)))
print("训练集:{:1f}".format(r2score(y_train,dt_train_pred)))
print('均方误差:{:1f}'.format(M_S_E(y_test,dt_test_pred)))
print('平均绝对误差:{:1f}'.format(MAE(dt_test_pred,y_test)))
#print('平均误差率:{:1f}'.format(mean_absolute_percentage_error(y_test,dt_test_pred)))
print(mean_absolute_percentage_error(y_test,dt_test_pred))
y_test = pd.DataFrame.reset_index(pd.DataFrame(y_test),drop=True)
dt_test_pred = round(pd.DataFrame(dt_test_pred),2)
conpare = pd.concat([y_test,dt_test_pred],axis=1)
conpare = np.array(conpare)
print(conpare[300:500])