论文笔记--Augmenting Pre-trained Language Models with QA-Memory for Open-Domain Question Answering
论文笔记--Augmenting Pre-trained Language Models with QA-Memory for Open-Domain Question Answering
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
-
- 3.1 QA
- 3.2 QAMAT(QA-Memory-Augmented Transformer)
-
- 3.2.1 Encoder
- 3.2.2 Dense Retriver
- 3.2.3 Neural Memory Integration
- 3.2.4 Neural+Discrete Memory Integration
- 3.3 QAMAT+
- 3.4 Two-Stage Pretraining
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:Augmenting Pre-trained Language Models with QA-Memory for Open-Domain Question Answering
- 作者:Wenhu Chen, Pat Verga, Michiel de Jong†, John Wieting, William W. Cohen
- 日期:2023
- 期刊:arxiv preprint
2. 文章概括
文章给出了一种ODQA(Open Domain Question Answering)方法QAMAT,该方法基于两阶段的训练框架,在现有RePAQ的基础上节省了内存和计算量,在多个QA benchmarks上取得更好的表现。
3 文章重点技术
3.1 QA
QA(Question Answering)可分为CBQA(Closed-Book)和ODQA(Open Domain):
- CBQA:基于大量语料库训练一个QA模型,然后直接询问模型得到答案。
- ODQA:一般来说会首先对语料库进行检索,然后对检索结果进行阅读理解,给出最终的答案。
现有的ODQA中的SOTA方法为RePAQ,即在推理阶段直接访问存储的QA对,检索和当前问题相似的Q,最终基于这些问题的回答得到现有问题的答案。但上述方法有以下局限性: 1)这种方法需要大量的监督数据以供问题检索,故一般来说RePAQ需要动态更新检索库,但这个更新过程本身又是昂贵且复杂的。2)RePAQ只支持检索显式存储于索引中的问题,很难满足复杂检索的需求。
3.2 QAMAT(QA-Memory-Augmented Transformer)
为了解决上述问题1),文章提出了一种QAMAT方法。具体来说,输入文本 X = x 1 , … , x n X=x_1, \dots, x_n X=x1,…,xn,其中 X X X可能为预训练阶段的段落或者微调阶段的问题(Q),模型的预训练任务为:给定语料库 ( X , { Q k , Q k } k = 1 m ) (X, \{Q^k, Q^k\}_{k=1}^m) (X,{Qk,Qk}k=1m),其中 A i A^i Ai为对应 Q i Q^i Qi在 X X X中的spans,我们从 X X X中随机采样 k k k个样本,并将对应 A i A^i Ai的位置替换为[MASK],模型需要尝试预测这些[MASK]对应的token。上述预训练目标为 P ( Y ∣ X ) = ∑ m i ∈ M p ( Y ∣ X , m i ) p ( m i ∣ X ) (1) P(Y|X) = \sum_{m_i\in M} p(Y|X, m_i)p(m_i|X)\tag{1} P(Y∣X)=mi∈M∑p(Y∣X,mi)p(mi∣X)(1),其中 M M M为存储的所有问题对。
3.2.1 Encoder
文章采用了T5[1]的Encoder-Decoder基本架构。其中编码函数 f θ : X → F θ ( X ) ∈ R n × d f_{\theta}: X\to \mathcal{F}_{\theta}(X) \in \mathbb{R}^{n\times d} fθ:X→Fθ(X)∈Rn×d将输入序列 X X X映射为一个向量,然后该向量的指定位置元素被用于表征query和memory:当前问题 X X X的[MASK]分词对应的嵌入 f θ ( X , [MASK] ) ∈ R d f_{\theta}(X,\text{[MASK]}) \in \mathbb{R}^{d} fθ(X,[MASK])∈Rd被用来表征query, memory中的key(Q)和value(Q+A)的[CLS]分词对应的嵌入 f θ ( m i k , [CLS] ) , f θ ( m i v , [CLS] ) ∈ R d f_{\theta}(m_i^k, \text{[CLS]}) , f_{\theta}(m_i^v, \text{[CLS]}) \in \mathbb{R}^{d} fθ(mik,[CLS]),fθ(miv,[CLS])∈Rd分别用于表征被访问的memory中的Q和A。
3.2.2 Dense Retriver
定义Memory为 M M M,包含上述key-value对。其中 m i k ∈ M m_i^k \in M mik∈M为一个问题,对应的 m i v m_i^v miv为问题和对应的回答合并"Q+A"。考虑到上述(1)式的计算量,我们可以通过获得和当前问题相似的Top- K ( M ) K(M) K(M)进行模拟。为了检索出Top- K ( M ) K(M) K(M),先用模型对当前的问题 X X X和所有 m i k m_i^k mik进行编码,然后计算 X X X的编码与每个候选问题 m i m_i mi编码的相似度(内积),找到和当前 X X X最相似的 K K K个问题对。
3.2.3 Neural Memory Integration
现在我们获取到和当前问题比较相似的 K K K个QA对,接下来需要把这些数据整合得到当前问题的回答。为此,文章将 m i v m_i^v miv通过如下方式整合进入encoder:
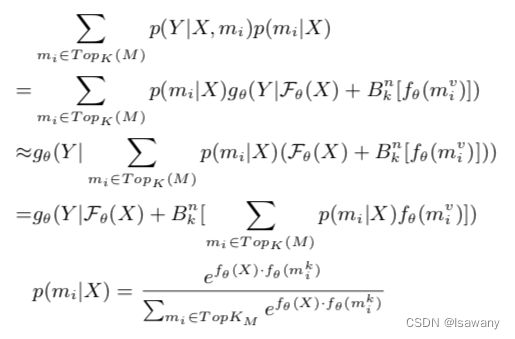
文章的训练目标(1)可近似为上式,其中概率 P ( Y ∣ X , m i ) P(Y|X, m_i) P(Y∣X,mi)可由解码函数 g θ g_{\theta} gθ表示,解码的输入为 X X X的向量嵌入 F θ ( X ) \mathcal{F}_{\theta}(X) Fθ(X)和候选问答 m i v m_i^v miv的[CLS]嵌入的广播形式 B k n [ f θ ( m i v ) ) ] B_k^n[f_{\theta}(m_i^v))] Bkn[fθ(miv))],其中广播算子 B k n ( x ) = [ 0 , … , x T , … , 0 ] B_k^n (x) = [\bold{0}, \dots, x^T, \dots, \bold{0}] Bkn(x)=[0,…,xT,…,0],即除了第 k k k行(列?)其余均为0。记上式条件概率的条件为 H ( X , T o p K ( M ) , p ( x ∣ X ) ) H(X, Top_K(M), p(x|X)) H(X,TopK(M),p(x∣X)),则我们的训练目标变为 p ( Y ∣ X ) = g θ ( Y ∣ H ( X , T o p K ( M ) , p ( x ∣ X ) ) ) . (2) p(Y|X) = g_{\theta} (Y|H(X, Top_K(M), p(x|X))) \tag{2}. p(Y∣X)=gθ(Y∣H(X,TopK(M),p(x∣X))).(2)上述过程可表示为下图的上半部分。
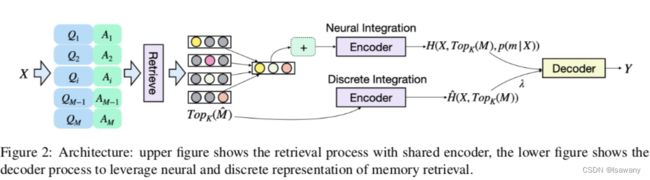
3.2.4 Neural+Discrete Memory Integration
上述广播算子的输入为 ∑ i p ( m i ∣ X ) f θ ( m i v ) ∈ R d \sum_i p(m_i|X) f_\theta (m_i^v) \in \mathbb{R}^d ∑ip(mi∣X)fθ(miv)∈Rd,表示topK文档的所有 m i m_i mi的汇总(加权求和)。为了让模型更好地利用每个 m i m_i mi自身的信息,文章增加了离散输入 X ^ = C o n c a t [ m k ; … ; m i ; X ] ∈ R ( n + k ∣ m ∣ ) × d \hat{X} = Concat[m_k;\dots ;m_i; X] \in \mathbb{R}^{(n+k|m|) \times d} X^=Concat[mk;…;mi;X]∈R(n+k∣m∣)×d,再对该输入进行编码,得到 H ^ ( X , T o p K ( M ) ) \hat{H}(X, Top_K(M)) H^(X,TopK(M)),最终基于 H ^ \hat{H} H^和 H H H进行预测: P ( Y ∣ X ) = g θ ( H ′ ( X , T o p K ( M ) , p ( m ∣ X ) ) + λ H ^ ( X , T o p K ( M ) ) ) (3) P(Y|X) = g_{\theta}(H'(X, Top_K(M), p(m|X)) + \lambda \hat{H}(X, Top_K(M))) \tag{3} P(Y∣X)=gθ(H′(X,TopK(M),p(m∣X))+λH^(X,TopK(M)))(3),其中 H ′ ( … ) = [ 0 ∣ m ∣ × d ; H ( … ) ] H'(\dots) = [\bold{0}^{|m|\times d}; H(\dots)] H′(…)=[0∣m∣×d;H(…)]为了令 H , H ^ H, \hat{H} H,H^的维度相同。
3.3 QAMAT+
为了处理Multi-Hop任务(即结合多个文本进行阅读理解),文章提出了一种级联的架构QAMAT+。假设对一个two-hop任务,我们先使用 X X X进行query得到第一轮的Top- K ( M ; 1 ) K(M;1) K(M;1)和 f θ f_{\theta} fθ;接下来我们令 X 1 = [ T o p K ( M ; 1 ) ; X ] X^1 = [Top_K(M;1); X] X1=[TopK(M;1);X]作为第二轮的query,得到新的Top − K ( M ; 2 ) -K(M;2) −K(M;2),最后计算 X 1 X^1 X1和Top − K ( M ; 2 ) -K(M;2) −K(M;2)对应的条件概率,整体结构如下图
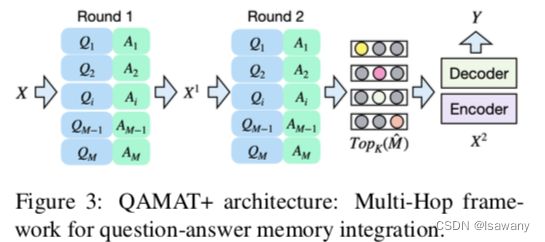
3.4 Two-Stage Pretraining
为了提升训练效率,文章提出了两阶段的训练框架:
- In-Batch Pretraining:第一阶段只考虑每个batch内部的样本。假设batch大小为 B B B,包含样本 { X i , { Q i k , A i k } k = 1 K } i = 1 B \{X_i, \{Q_i^k, A_i^k\}_{k=1}^K\}_{i=1}^B {Xi,{Qik,Aik}k=1K}i=1B,其中每个样本 X i X_i Xi都有 K K K个从 X i X_i Xi种得到的QA对,此外,我们再通过BM25方法生成K个hard-negative。最终得到 2 K 2K 2K个QA对的memory M ^ \hat{M} M^,得到memory 编码函数 f θ f_{\theta} fθ,(此阶段旨在训练一个in-batch index/query encoder(query和index共享))
- Global Pretraining and Fine-Tuning:在全局训练过程,我们冻结上述memory编码 f θ f_{\theta} fθ,并基于全局的memory-key对上述编码进行query得到全局的top-K候选,且更新query的参数。(此阶段旨在训练一个global query encoder,保持index encoder不变)
4. 文章亮点
文章提出了一种QAMAT框架,有效改善了RePAQ无法高效更新QA对且难以检索复杂问题的现状。数值实验表明,QAMAT比RePAQ的效果有显著提升,且大幅节省了性能开销。此外,QAMAT+在multi-hop问答任务上表现出色,可作为未来出来multi-hop任务的一种候选手段。
5. 原文传送门
Augmenting Pre-trained Language Models with QA-Memory for Open-Domain Question Answering
6. References
[1] 论文笔记–Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer