竞码编程-蓝桥杯模拟赛5（大学生组&青少年组）

A. 试题A：摆正方形 5

描述

JM有一些边长为11的小正方形，他想通过手中的小正方形，摆出各种边长的大正方形。

为了庆祝自己周末快乐，JM决定一次性摆出边长为11至130130的所有正方形。

请问，JM总共需要多少个小正方形。

边长位1，2，3的正方形

例如：一次性摆出1至3的所有正方形需要14个小正方形

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个数字，填写多余的内容将无法得分。

思路：找规律

code:

#include
using namespace std;
int main()
{
    int ans=0,n;
    while(true)
    {
        ans=0;
        cin>>n;
        for(int i=1;i<=n;i++)
        ans+=i*i;
        cout<

B. 试题B：打靶射击 6'

JM非常喜欢玩气球射击游戏，已知气球总共有三种颜色：红、绿、蓝。

击中蓝色气球得99分，击中红色气球得55分，击中绿色气球得22分。JM总共射击了10次，每一次都有击中一个气球，而且每一种颜色至少被击中了一次。JM共10次射击总得分61分，击中了几次绿色气球.

请输出击中了几次绿色气球。

思路：枚举

#include
using namespace std;
int main()
{
    int x,y,z;
    for(int i=1;i<=10;i++)
    {
        for(int j=1;j<=10;j++)
        {
            for(int k=1;k<=10;k++)
            {
                if(i+j+k==10&&9*i+5*j+2*k==61)
                cout<<"蓝色："<

C. 试题C：九溪十八涧 11'

描述

重重叠叠山,

曲曲环环路,

丁丁东东泉,

高高下下树

-----俞曲园(清末)

这首诗，暗藏玄机。

重+重叠=叠山，曲+曲环=环路，丁+丁东=东泉，高+高下=下树。

刚好可以写成四个A+AB=BC的等式，AB表示一个两位数，个位是B，十位是A；BC表示一个两位数；个位是C，十位是B。

按照字典序输出四个解A B C。每行一个解，相邻两个数字用空格隔开。

例如：5 + 56 = 61，A = 5， B = 6，C = 15+56=61，A=5，B=6，C=1

提示：字典序最小的解为：5 6 1，且A,B,C互不相等

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果四行，在提交答案时只填写这四个解，填写多余的内容将无法得分。

思路：模拟

#include
using namespace std;
bool judge(int a,int b,int c)
{
    if(a==b||b==c||a==c)return false;
    if(a>=10||b>=10||c>=10)return false;
    return true;
}
int main()
{
    for(int a=0;a<=100;a++)
    {
        for(int b=0;b<=100;b++)
        {
            for(int c=0;c<=100;c++)
            {
                if((a+a*10+b==b*10+c)&&judge(a,b,c))
                cout<

D. 试题D：完美数字 15'

描述

JM新研究出了一种完美数字，他是这样定义的：如果一个数字x的数位之和sum是一个平方数或者立方数，且x的数位中没有出现数字2，42，4,则称x为完美数字。

前1010个完美数字为：1，8，9，10，13，17，18，31，35，361，8，9，10，13，17，18，31，35，36

请你帮JM统计一下，[1,141516]中有多少个这样的完美数字。

 

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个数字，填写多余的内容将无法得分。

思路：模拟

#include
#include
using namespace std;
int cnt;
bool pingfang(int n)
{
    int temp=sqrt(n);
    if(temp*temp!=n)return false;
    return true;
}
bool lifang(int n)
{
    for(int i=1;i<=n;i++)
    {
        int temp=i;
        if(temp*temp*temp==n)return true;
        if(temp*temp*temp>n)return false;
    }
}
bool judge(int n)
{
    while(n)
    {
        int temp=n%10;
        if(temp==2||temp==4)return false;
        n/=10;
    }
    return true;
}
int f(int n)
{
    int t=0;
    while(n)
    {
        int temp=n%10;
        t+=temp;
        n/=10;
    }
    return t;
}
int main()
{
    int n=141516;
    //cin>>n;
    for(int i=1;i<=n;i++)
    {
        int t=f(i);
        if((pingfang(t)||lifang(t))&&judge(i))
        {
            cnt++;
            //cout<

E. 试题E：三角填数 17'

描述

 

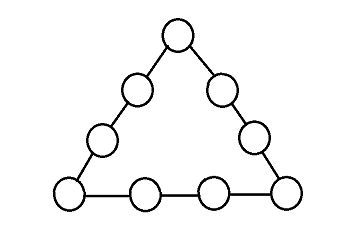
填入1-91−9数字，每个数字填一次，问有多少种方案使得三条边的数字之和相等。注意，只要有一个位置上的数不相同，则认为是两种不同的方案。

如图P1P1所示，是一种合法方案

P1

注意：三角形的每一个位置是固定的，不能够旋转。

 

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数(偶数)，在提交答案时只填写这个数字，填写多余的内容将无法得分。

思路：全排列

#include
#include
using namespace std;
int main()
{
    int a[9]={1,2,3,4,5,6,7,8,9};
    int cnt=0,n=9,x,y,z;
    do{
        x=a[0]+a[1]+a[2]+a[3];
        y=a[3]+a[4]+a[5]+a[6];
        z=a[6]+a[7]+a[8]+a[0];
        if(x==y&&y==z)
        {
            cnt++;
            cout<

F. 试题F：A+B 10'

描述

JM重新定义了加法运算。

两个长度为nn位的数字A,B做加法运算A+B，其结果C也是一个n位数,C的每一位为对应位置上A，B较小的数字。

输入

输入一个行，两个位数相等的两个数字，中间用空格隔开

输出

输出A+B的结果

样例

输入复制

456 178

输出复制

156

输入复制

123456789 987654321

输出复制

123454321

输入复制

0 0

输出复制

0

提示

样例1解释

A = 456, B = 178 , A + B = min(4, 1) min(5, 7) min(6, 8) = 156

数据规模

对于20%的数据，A = B, A <= 100000A=B,A<=100000

对于50%的数据，A，B<= 10^{18}

对于100%的数据，|A|=|B|<= 10^4，∣A∣表示数字A的位数。

#include
#include
using namespace std;
string a,b;
int c[100000];
int main()
{
    int n;
    cin>>a>>b;
    n=a.size();
    for(int i=0;i

G. 试题G：圈地养猪 15'

描述

由于猪价暴涨，JM准备圈地养猪。

但是猪崽从哪来呢？当然是去抓野山猪咯~

已知每一头野山猪的坐标，现在JM需要用围栏围成一个矩形，在矩形内的猪就都属于JM了。围起来的野山猪当然是越多越好啦，贪心的JM想把所有的野山猪给围起来。但是JM不知道得准备多长的围栏。你能帮JM吗计算一下至少需要多长的围栏，围成的矩形能够把所有的野山猪围起来。

注意：

1. 围栏的四个角必须在整数坐标点上，而且有野山猪的点是不能够构建围栏的~

2. 所围矩形的边必须平行于x或者y轴。

输入

第一行输入一个整数nn，表示野山猪的头数

接下来nn行，每行输入两个整数x\ yx y，表示野山猪所处的位置(x,y)(x,y)

输出

输出一个整数，表示需要的围栏长度

样例

输入复制

4
0 0
1 1 
2 2
3 3

输出复制

20

输入复制

5
44 62
34 69
24 78
42 44
64 10

输出复制

224

输入复制

4
1 100
1 0
1 -100
1 0

输出复制

408

提示

样例1解释

 

数据规模

对于50\%50%的数据，2 \le n \le 100, x = 12≤n≤100,x=1

对于100\%100%的数据，2 \le n \le 10000, -1000000 \le x, y \le 10000002≤n≤10000,−1000000≤x,y≤1000000，一个坐标点上可能会有多头野山猪

思路：找两个坐标即可，两种情况，一种左下右上，一种左上有下。最后往外扩一层

#include
#include
using namespace std;
int x1,y1,x2,y2;
int main()
{
    int n,x,y,ans=0;
    cin>>n;
    cin>>x>>y;
    x1=x;y1=y;x2=x;y2=y;
    for(int i=2;i<=n;i++)
    {
        cin>>x>>y;
        x1=min(x1,x);
        x2=max(x2,x);
        y1=min(y1,y);
        y2=max(y2,y);
    }
    if(x1<=x2&&y1<=y2)
    {
        x1-=1;y1-=1;
        x2+=1;y2+=1;
        ans=abs(x1-x2)*2+abs(y1-y2)*2;
    }
    else
    {
        x1-=1;y1+=1;
        x2+=1;y2-=1;
        ans=abs(x1-x2)*2+abs(y1-y2)*2;
    }
    cout<

H. 试题H：友好搭档 21'

描述

JM在学习了素数之后，决定挑3个素数构成和为n,并将这样一组的三个数称之为友好搭档

现在，JM同学想知道，它能够找出多少组不同的友好搭档。

例如：(2,2,5)(2,2,5)就是一组和为99的友好搭档

注意：同组元素没有先后次序关系，(2,2,5)和(2,5,2)(2,2,5)和(2,5,2)是同一组友好搭档

输入

输入一行，一个正整数nn。

输出

输出和为nn不同友好搭档的数量

样例

输入复制

9

输出复制

2

提示

样例解释

(2,2,5),(3,3,3)(2,2,5),(3,3,3)

数据规模

对于50\%50%的数据，1 \le n \le 1001≤n≤100

对于80\%80%的数据，1 \le n \le 20001≤n≤2000

对于100\%100%的数据，1 \le n \le 800001≤n≤80000

思路：首先要找的就是素数（打表）现在素数全部找出来之后开始组合，记住去重

 

#include
#include
#include
#include
using namespace std;
const int maxn=81000;
int prime[maxn],vis[maxn],cnt,n,vis1[maxn],answer;
int visit1[maxn],visit2[maxn],visit3[maxn];
void Prime()
{
    
    for(int i=2;i<=n;i++)
    {
        if(!vis[i])
        {
            vis[i]=1;
            vis1[i]=1;
            prime[cnt++]=i;
            for(int j=i*i;j<=n;j+=i)
            vis[j]=1;
        }
    }
}
struct node{
    int x,y,z;
    
};
queueans;
int main()
{
    cin>>n;
    Prime();
    for(int i=0;i0&&vis1[temp])
            {
                node t;
                t.x=prime[i];t.y=prime[j];t.z=temp;
                ans.push(t);
            }
        }
    }
    while(!ans.empty())
    {
        node t=ans.front();
        ans.pop();
        int a[3];
        a[0]=t.x;a[1]=t.y;a[2]=t.z;
        sort(a,a+3);
        if(!visit1[a[0]]||!visit2[a[1]]||!visit3[a[2]])
        {
            visit1[a[0]]=1;visit2[a[1]]=1;visit3[a[2]]=1;
            answer++;
            //cout<

总结：最后两组应该是超时了，可能线性筛会过把（待更）

  最后两题坐等官方题解（qaq）

更新：

#include
#include
#include
#include
using namespace std;
const int maxn=81000;
int prime[maxn],vis[maxn],cnt,n,answer;
void Prime()//素数打表 
{
	
	for(int i=2;i<=sqrt(n);i++)
	{
		if(!vis[i])
		{
			//vis1[i]=1;//一开始在内部统计素数以及他的个数，而这样i不能取sqrt(n)，只能去i=n,效率低 
			//prime[cnt++]=i; 
			for(int j=i*i;j<=n;j+=i)
			vis[j]=1;
		}
	}
}
int main()
{
	cin>>n;
	Prime();
	//统计素数
	for(int i=2;i<=n;i++)//在外部统计素数以及他的个数 
	if(!vis[i])
	prime[cnt++]=i; 
	
	for(int i=0;i1&&!vis[temp]&&temp>=prime[j])//保证temp>=peime[j]，（a<=b<=c）避免去重操作 
			{
				//cout<

I. 试题I：调皮的JM 25'

描述

在竞码小学，JM同学是捣蛋三巨头之一，调皮的很。

有一次，在课外活动的时候，JM同学偷偷跑到老师办公室玩耍，一不小心把英语老师电脑上准备上课用的英文文章给删掉了，导致英语老师暴跳如雷，生气的很~

老师给了JM一个改过自新的机会，如果JM能够找出删除的文章HH中出现了多少个子串与字符串SS等价，那么老师将原谅JM同学，否则，请家长是免不了的~

对于两个字符串等价，我们的定义为：两个字符串按照字典序排序后相同，则认为是等价字符串。

例如：aabaab 和 baabaa 两个字符串为等价字符串

abaaba 和 bbabba 则不是等价字符串。

输入 第一行输入一个字符串SS

第二行输入一个字符串HH

输出 输出子串个数

样例 输入复制 aab abacabaa 输出复制 3 提示 样例解释

第一个等价子串 aba cabaa

第二个等价子串 abac aba a

第三个等价子串 abaca baa

数据规模

对于50%的数据，|S|,|H| <= 2000∣S∣,∣H∣<=2000

对于100%的数据，|S|,|H| <= 100000∣S∣,∣H∣<=100000，保证输入的字符串只有小写字母

思路：50分做法：

#include
#include
#include 
#include
using namespace std;
const int maxn=110000;
char s[maxn],h[maxn],t[maxn];
int lens,lenh,len,ans;
bool cmp(char a,char b)//给字符串排序 
{
	return a>s>>h;
	lens=strlen(s);lenh=strlen(h);
	sort(s,s+lens,cmp);//给子串排序 
	for(int i=0;i<=lenh-lens;i++)//枚举模式串 
	{
		len=0;
		for(int j=i;j

100分做法：用前缀和的思想

#include
#include
#include
using namespace std;
string s,h;
int ans;
vectorcnts(26),cntt(26);
int main()
{
	cin>>s>>h;
	for(int i=0;i=s.size())
		cntt[h[i-s.size()]-'a']--;//只统计长度为lens区间的字符串个数 
		if(cnts==cntt)//相等说明2个vector具有相同的容量。所有位置的元素相等 
		ans++;
	}
	cout<

 

J. 试题J：冷嘲热讽 25’

描述

JM自从学习了约瑟夫问题，就特别感兴趣，研究了很久。设计了一个类似的游戏，取名叫做冷嘲热讽。

总共有NN个人参与游戏，一字排开，从左往右编号1，2，...，N1，2，...，N，每一个人初始有一个能力值A_iAi​。

每一轮，每一个人同时向嘲讽右边的人，如果被嘲讽的能力值比嘲讽的人大(A_i < A_{i + 1}Ai​

一轮结束，没被淘汰的人向左靠齐，调整站位，重新编号1，2，...，1，2，...，，进入下一轮。

当不再会有人被淘汰时，游戏结束。

现在JM想知道，这个游戏要多少轮才会结束。你能帮帮他吗？

输入

第一行输入11个整数NN，表示总共有NN个人参加游戏。

第二行NN个整数A_iAi​。

输出

一个整数，表示游戏要多少轮才会结束。

样例

输入

复制

7
6 5 8 4 7 10 9

输出

复制

2

输入

复制

5
2 4 6 8 3

输出

复制

2

输入

复制

3
3 2 1

输出

复制

0

提示

样例1解释

初始状态：6 5 8 4 7 10 9

第一轮：6 5 4 9

第二轮：6 5 4

样例2解释

初始状态：2 4 6 8 3

第一轮：2 3

第二轮：2

数据规模

30\%30%的数据，满足1≤N≤10^41≤N≤104;

50\%50%的数据，满足 1≤N≤10^51≤N≤105;

100\%100%的数据，满足1≤N≤10^6, 0≤Ai≤10^91≤N≤106,0≤Ai≤109.

思路：模拟

#include
#include
#include
using namespace std;
const int maxn=1100000;
int a[maxn],b[maxn];
int ans,flag,cnt;
int main()
{
	int n;
	cin>>n;
	for(int i=0;i>a[i];
//	for(int i=0;ia[i-1])
			{
				//vis[i]=1;
				flag=true;
			}
			else
			{
				b[cnt++]=a[i];			
			}
		}
		if(!flag)break;		
		ans++;
		for(int i=0;i

官方题解：单调栈