2022, Q1(Applied Soft Computing), Semantics in Multi-objective Genetic Programming

---

Abstract

语义已成为遗传程序设计 (GP) 研究的重点课题。语义是指 GP 个体在数据集上运行时的输出(行为)。大多数关注单目标 GP 中语义多样性的工作表明它在进化搜索中是非常有益的。令人惊讶的是，多目标 GP (Multi-Objective GP，MOGP) 在语义方面的研究微乎其微。在这项工作中，我们超越了对 MOGP 中语义的理解，提出了 SDO：基于语义距离作为一个额外的标准。这自然鼓励了 MOGP 中的语义多样性。为此，我们在第一个帕累托前沿(最有前途的前沿)的密度较小区域找到一个支点。然后用它来计算枢纽与种群中每个个体之间的距离。然后将得到的距离作为一个额外的标准进行优化，以有利于语义多样性。我们还使用了另外两种基于语义方法作为基线，称为基于语义相似度的方法. 此外，我们还使用非支配排序遗传算法-II (Non-dominated Sorting Genetic Algorithm II,NSGA-II) 和强度 Pareto 进化算法 2 (Strength Pareto Evolutionary Algorithm 2) 进行比较。我们使用高度不平衡的二分类问题，一致地展示了我们提出的 SDO 方法如何产生更多的非支配解和更好的多样性，从而导致更好的统计显著性结果，使用超体积结果作为评估措施，与其他 4 种方法相比。

1. Introduction

遗传规划 [1] 是 4 种典型的进化算法范式之一，由Koza于20世纪90年代初提出。多年来，研究人员一直对使GP更适合进化搜索感兴趣。已被证明使GP更加健壮的一个关键要素是语义。后者已成为全科医生研究的重点课题。语义可以看作是GP程序的行为。该行为是GP程序在一组适应度案例上执行时的输出。

得益于研究领域发现的有希望的结果，GP语义学的科学出版物数量显著增加。我们在第二节讨论了GP中语义学的一些相关工作。有趣的是，这些工作绝大多数都集中在单目标GP (SOGP) 上，在多目标GP (MOGP)上进展甚微，只有[ 2、3、4、5]例外。因此，这项科学工作大大扩展了这一研究领域，并在MOGP环境中使用了三种语义形式。分别与两种成熟的进化多目标优化(EMO)方法进行比较：非支配排序遗传算法-II (NSGA-II) [6]和强度Pareto进化算法(SPEA2) [7]。本研究采用的基于语义的MOGP方法是：

Semantic Similarity-based Crossover. (SSC).这是由文献[8]中提出的SOGP方法所激发的。这种方法是SOGP语义学中早期的方法之一，作者能够在连续搜索空间中推广这种方法。我们在MOGP中扩展了这个著名的方法。

Semantic-based Crowding Distance. (SCD). 这里的主要思想是将EMO算法中常用的拥挤距离替换为基于语义的距离，该距离最初是在第一作者的MOGP工作[3、4]中研究的。

Semantic-based Distance as an additional criteriOn. (SDO). 该方法借鉴了SCD，并使用产生的语义距离作为另一个组件来优化EMO算法，在[5]中简要研究。

使用这三种基于语义的方法可以让我们展示以下内容：

首先，通过使用SSC，我们展示了在单目标GP中，在交叉算子中计算并用于成功促进语义多样性的语义距离如何在MOGP中没有同样的积极影响。

其次，通过使用SCD，受EMO中常用的拥挤距离的启发，我们证明了在种群中的每个GP树和一个"枢纽"之间可以自然地计算语义距离。后者是位于第一Pareto前沿最稀疏区域的个体。然后SCD远离SSC，它通过反复使用交叉来强迫多样性出现，从而促进语义多样性，如[8]。

最后，我们借鉴SSC和SCD在语义上的理解，为MOGP中语义多样性的出现提出了一个健壮的机制。特别地，我们使用语义距离值作为一个额外的指标来进化种群。这自然地促进了MOGP中的语义多样性，从而在一系列高度不平衡的数据集中，基于演化的Pareto近似集相对于其他四种方法(两种基于语义的方法和两种EMO方法)的平均超体积获得了更好的、具有统计学意义的结果。

1.1. Main contributions of this scientific study

在前期工作[5]中，我们对多目标遗传规划(Multi-Objective Genetic Programming，MOGP)中的语义进行了初步的限定研究。具体来说，我们首先提出并使用了三种基于语义的方法，分别是基于语义相似度的交叉方法(Semantic Similaritybased Crossover，SSC)、基于语义距离的附加标准方法(Semantic-based Distance as an additional criteriOn，SDO)和基于枢纽相似度的附加标准方法(Pivot Similarity Semantic-based Distance as an additional criteriOn，PSDO)。

我们的初步研究的主要结论是，使用SDO或PSDO中计算的基于语义的距离值作为EMO环境中的另一个待优化目标，具有足够的鲁棒性，优于著名的NSGA-II和SPEA2方法的结果。此外，在我们最初的研究中，我们发现从搜索空间中最远的点枢轴计算到种群中每个个体的距离，并将其作为在EMO环境中优化的额外标准，可以提高基于语义的方法的性能。此外，我们能够微调如何计算这个距离来显著提高进化搜索。这是用SDO方法实现的，这在本文中再次使用。然而，值得一提的是，这些结论来自于最初的有限研究，包括有限的统计分析阻碍了一般结论的得出，有限的结果以及缺乏解释，这有助于我们清楚地说明为什么SDO比各自的规范方法以及其他两种基于语义的方法产生更好的结果。

在这项工作中，我们解决了所有这些问题。具体来说，本科学研究的主要贡献如下：

• 我们一致地展示了在多目标GP (MOGP)设置中，单目标GP中使用的、被广泛报道在GP中有益的基于语义相似度的交叉(SSC)如何不具有相同的积极影响。
• 由此，我们展示了基于语义的距离方法如何增强MOGP中的进化搜索。为此，我们使用了两种基于语义的方法：基于语义的拥挤距离(SCD)和作为附加标准的语义距离(SDO)。
• 我们展示了SDO如何比本文中使用的所有方法产生更好的结果，包括基于语义的方法和典型的EMO方法。
• 这项科学研究的另一个主要贡献是包含了使用两种成熟的EMO方法NSGA-II和SPEA2的详细结果。通过这样做，相对于[5]中报告的有限结果，我们现在能够通过进行系统的统计分析得出合理的结论，在第6节中详细解释。
• 这项工作的另一个重要贡献是，我们能够解释为什么SDO中使用的基于语义的技术倾向于改进进化搜索。我们通过广泛分析SDO在唯一解的数量、解的世代重复频率等方面的行为来实现。

现将此项工作整理如下。本工作的相关研究见第2节。第3节讨论了语义和MOPG的基本背景。第四部分介绍了本文提出并使用的MOGP语义方法。实验设置见第5节。第6节详细介绍了所有MOGP语义方法(SSC、SDO和SCD)和EMO方法(NSGAII和SPEA2)的结果。这也解释了为什么SDO比其他算法有更好的结果。在第7节中，我们得到了一些结论。

2. Relevant Work

2.1. Semantics

语义学已成为GP研究的一个重要课题，并提出了多种定义。语义可以看作GP程序的行为(在数据集上记录输出)。我们在第3节给出了语义的形式化定义。在过去的十年中，GP中的语义研究有了显著的增长，这是因为当语义在进化搜索中得到推广时，研究社区报告的结果比那些没有明确促进语义的GP方法更好。这些研究的重点从处理直接语义方法，如几何算子的使用[9]，到分析间接语义方法[3、8]。接下来，我们讨论了这方面的一些相关工作.

McPhee等人的分析。[10]为间接语义作品奠定了基础。他们的研究主要集中在分析布尔问题的程序子树和上下文(上下文是子树被移除后程序的剩余部分)的语义。这项研究的一个关键结果证明，常用的比例90-10交叉产生了高比例的个体，这些个体在语义上是等价的。换句话说，大多数的交叉事件并没有导致对语义空间的有效搜索，从而限制了执行该操作的潜在性能收益。

为了克服这个问题，Beadle和Johnson [11]提出了一种有助于促进语义多样性的算子，称为语义驱动的交叉(SDC)。为了验证父代与子代是否等价，为此，作者使用了简化的有序二元决策图。在他们的研究中，当父代和子代在语义上对等时，作者多次使用交叉。后来，Beadle和Johnson [12]也探索了类似的变异算子技术，称为语义驱动变异(Semantically Driven Variation，SDM)。这验证了父代和子代之间的语义等价性，其中子代是通过将一个子树替换为另一个随机生成的子树生成的。这种等价性分析是通过将子代化简为典范形式来进行的，而典范形式可以很容易地与它的父代进行比较。他们报告说，这两种技术都增加了语义多样性，并导致改进的进化搜索。

这些方法的一个缺点是使用离散的适应值情况，因此限制了它们对连续搜索空间的适用性。Uy等[13]通过在连续搜索空间中使用巧妙的语义交叉算子的激励方法克服了这一局限性。通过评估来自给定问题域的点的预定义样本来近似语义。因此，两个表达式(两棵树或两棵子树)的语义等价性可以通过这些表达式输出的绝对差值来计算。如果这两个表达式的差值落在一个预定义的阈值(一个称为语义敏感度的参数)的范围内，那么这些表达式可以被认为是语义等价的。Uy等人提出了4种不同的场景来实现这种形式的语义，其中前两种场景处理子树的语义。场景I通过检查交叉操作中使用的子树的语义等价性来促进语义多样性，如果它们被认为是等价的，则保留父代。否则，再次应用交叉，但现在使用两个不同的随机选择的交叉节点。在场景II中，如果子树彼此等价，则选择它们。后两个场景通过考虑完整的程序树来考虑语义。场景III检查父代对子代的语义。也就是说，如果发现子代和父代树在语义上是等价的，则子代被丢弃，父代被保留到下一代。场景IV与场景III相同，但在这种情况下，条件发生了逆转，即如果满足语义等价条件，后代被保留到下一代。与其他三种方法相比，场景I在符号回归问题上表现出更好的效果。

没有保证在执行交叉操作后会立即找到语义等价的子代，并且上述方法的扩展引入了试错机制来多次执行交叉操作，直到找到合适的候选者或直到达到某个预定义的迭代[8]。然而，一个显著的缺点是Uy等人的方法计算量大。针对这一缺陷，Galv ’ an等人提出了一种经济有效的方法，试图通过锦标赛选择算子来促进语义多样性。第一亲本的选择与往常一样。第二个父代是通过考虑：语义相异性和适应度来选择的。如果没有与第一个父代不相似的个体， 然后按照锦标赛选择中常用的方法选择第二个父代。语义相异度的获取与Uy等人[13]的方法相同，并在场景I中进行了描述。这种经济有效的方法与Uy等人的方法类似，其优点是消除了昂贵的试错机制。

Forstenlechner等人[14]研究了语义在程序合成中的应用，这是一个不同于(符号回归和布尔问题)之前的领域。这种方法使用多种不同的数据类型，而不仅仅是单一的数据类型。两个GP子树的语义存储在一对向量中。在他们的工作中，作者使用了两个条件来检查语义相似度：1) “部分变化”，表示至少一个词条的语义保持不变，但另一个词条的语义发生了变化；2) “任意变化”，表示任意项不同的向量。如果发生部分变化，两个子树进行交叉。如果不存在，则检查"任何变化"。作者在研究中使用的八个问题中有四个采用这两个条件时报告了更好的结果。语义方法的分析也被应用于间接语义的局部搜索方法中。例如，Dou和罗基特[15]测试了多种GP和局部搜索变体的混合，包括三种子树选择方法和四种替换策略。作者发现，与具有统计较小树大小的基线GP方法相比，基于语义的局部搜索在稳态或世代GP之后的表现显著更好。

由于与标准GP系统相比搜索性能的提高，直接语义方法在GP研究中也受到了关注。通过纳入直接语义的驱动动机是以前的间接方法被认为是浪费的[13、8]。为了解决这个问题，Moraglio等人[9]利用他之前的理论结果[16]，允许修改GP树的基因型使其与几何算子相关。这就产生了继承他们财产的后果。这导致通过构造形成一个锥形景观，为进化过程提供了一个"更容易"的搜索方向。然而，这种方法的一个潜在限制是它允许中立的存在。这可能是有益的，也可能是有害的，这取决于当前问题的特点- -例如，[17、18、19、20]，Galv ’ an和Poli对中立在不同类型问题中的作用进行了深入的解释。文献[9]中提出的方法的另一个局限性是这种对GP树的修改倾向于产生更大的个体。针对后者，Vanneschi等[21]提出了Moraglio方法的缓存实现。为此，作者将GP树的语义存储在一个表中，使得该过程确实有效。然而，Vanneschi等方法的一个局限性是GP个体的重建过程繁琐且在某些情况下难以获得。这是一个特别适用于需要表达式的应用场合的缺点。Uy等[22]采取了与Vanneschi等[21]不同的方法来处理个体的大小。Uy等人提出了子树语义几何交叉(SSGX)算子，允许它们控制个体的大小。但是，他们的做法有一定的局限性也如确定正确的values对于在GP系统中应用SSGX需要的多个参数。此外，它还基于昂贵的试错机制(在他们的工作中设置最多20个trial来搜索合适的子树)。

在文献[5]中，我们提出了基于语义的方法将它们集成到MOGP系统中。在这项初步研究中，我们能够在MOGP框架中自然地促进语义，使用从最佳帕累托前沿中提取的一个支点来计算它与种群中每个个体之间的语义距离。我们发现，与其典型的进化多目标变体相比，该距离及其变体倾向于产生更好的结果，在这种情况下，与著名的NSGA-II [6]和SPEA2 [7]算法相比。然而，文献[5]中报道的结果是有限的：缺乏解释为什么SDO方法比最初研究中使用的其他方法更容易产生更好的结果，缺乏深入的统计分析和对SDO方法局限性的讨论。相比之下，目前的工作解决了所有这些问题，我们应该在下一节中看到。特别地，我们详细地结合了SPEA2算法所得到的结果以及使用这种EMO方法的基于语义的变体，我们详细地解释了为什么SDO通过使用不同的元素来工作，比如种群中复制个体的频率。我们还对结果进行了详细的统计分析。

2.2. Multi-Objective Genetic Programming

多目标优化问题的目标是在同时考虑多个潜在冲突目标的基础上发现候选解。在GP的背景下，有许多方法可以实现这一点。从广义上讲，主要有两种方法。一种是将多个目标纳入到单个适应度函数中。另一种方法是利用候选解[23、24、25]之间的帕累托占优关系，分别考虑目标。由于进化多目标优化( EMO )的目的是在进化运行的目标中发现解决方案的最佳平衡，因此帕累托占优允许用一种直观的方法来处理多个(冲突的)目标。EMO的细节将在3.2节中进一步说明。EMO是EAs中最受欢迎和最活跃的研究领域之一，具有许多应用并经常取得令人印象深刻的结果[23、24、25]。接下来，我们讨论了GP系统中已经采用EMO的一些工作。

Bleuler et al等[26]提出了一种EMO方法来自然地控制偶数n-奇偶性问题的膨胀。作者定义了在MOGP框架内同时优化的两个目标；第一个目标是程序的适应度，第二个目标是程序树的大小。该方法与其他著名的控制膨胀的技术进行了比较，例如使用包含适应度和简约压力(恒定压力和自适应压力均被测试)的聚合单目标函数，以及通过两个阶段的优化过程。这种方式不仅在当时是新颖的，而且还演示了如何成功地控制GP bloat,与其他方法相比，可以更快地评估解决方案。

与本研究相关的是Bhowan等[27]开展的工作，其中作者使用MOGP在二进制不平衡类上找到了高精度，与成熟的机器学习分类方法相比取得了良好的效果。Galv ’ an等人也将MOGP用于同类型问题[2、3、4]。同样，Zhao通过将这种偏差小心地插入到适应度函数中，展示了如何成功地使用MOGP来定义对目标的部分偏好[28]。纳入这种嵌入的激励原因是，在现实生活场景中，分类错误往往是成本敏感的，对一个类的正确预测的好处可能会大大超过对另一个类的正确预测。例如，批准一笔不良贷款比否认一笔好贷款的成本更高。

Shao等[29]演示了如何使用自动生成的域自适应全局特征对图像进行分类。类似于Bleuler等[26]如何实现他们的优化过程，Shao等在他们的MOGP框架中使用个体的长度作为待优化的目标，其中第二个目标是分类错误率。Shao等人报告说，他们的MOGP方法与其他14种方法相比，包括两种基于神经网络的方法，都取得了更好的性能。

3. Background

本部分定义了与本文工作相关的一些基本概念，即语义、MO和EMO算法。

3.1. Semantics

我们使用了最初在[30]中定义的语义定义。对于一般的监督学习任务，特别是对于GP，通常将问题指定为一组输入-输出对，也称为适应度案例，其形式为 $T=(i{n}_i,o_i)$，其中 $i{n}_i\in I$ 为输入，$o_i\in O$ 为期望输出，$i=1，\cdot \cdot \cdot ，l$，其中 $l$ 为适应度案例的个数。程序$p$的语义$s(p)$被定义为程序根据问题的适应度案例集合中给定的输入计算的输出值向量。这在形式上定义为：

3.2. Multi-Objective Optimisation

多目标优化的目标是同时优化两个或多个目标函数。当考虑多个目标函数时，这些目标函数往往会发生冲突，因此重点是寻找一组折衷解作为全局最优变得不可实现。解决该问题的一种自然形式是利用帕累托占优关系：一个在搜索空间的解$x_1$被称为帕累托占优解$x_2$，如果对于所有目标，$x_1$至少和$x_2$一样好，对于至少一个目标，$x_1$严格更好。

在这项工作中，目标是最大化的。在第5节中定义的问题是二分类问题，其目标是最大化两个冲突目标的分类精度。帕累托占优概念定义为：(1)：

式中：$(S_i{)}_m$表示第$m$个目标中解$S_i$的值。反之，如果种群中没有其他解占优，则认为解是非支配解。一个MO问题的最优权衡解集被称为Pareto最优解集。因此，EMO算法的目标是找到这个集合的(一个很好的近似)。Pareto最优前沿是Pareto最优集的目标空间表示。在EMO算法中，Pareto占优被用不同的方式来处理这样的标准来偏向搜索。其中最广为人知的是优势度排序(dominance rank)[6]和优势度计数(dominance count)[ 26 ]。优势度排序是基于种群中支配另一个解的数量，这意味着较低的值是可取的。另一方面，占优数是某一特定解占优的解的数量，在这种情况下，更高的值是可取的。目前有两种流行的EMO算法包含了上述使用Pareto占优的方式，本文采用它们：使用优势度排序的非支配排序遗传算法II( NSGA-II ) [6]和使用优势度排序和优势度计数的强度Pareto进化算法(SPEA2) [26]

在NSGA-II中，支配排序被用作解$S_i$的适应度值。这表示为

另一方面，SEA2在计算个体的适应度值时使用和占优计数和占优排序。首先，为种群中的每个候选解赋予一个强度值$D$。这在形式上定义为，

$D$则决定了特定解$(S_i)$占优的解的个数.为了确定SPEA2中候选解i的适应度值，我们使用支配解i的所有解的强度。这表示为，

3.2.1. Diversity Preservation in Multi-objective Optimisation Through the Use of the Crowding Distance

帕累托占优不提供一个总序，这样就需要另一个准则来有效地比较搜索空间中的不同点，这是进化过程中执行选择和生存所必需的。一种方法是使用拥挤距离测度，使得人口稀少的区域比人口密集的区域更可取。在客观空间中通常使用拥挤距离来区分具有相同帕累托等级的个体，优先选择那些人口较少的区域。算法 1 展示了如何计算这个拥挤距离，改编自[6]。

3.2.2. MOGP Algorithm

本文采用的MOGP框架是基于NSGA-II的，下面对其进行介绍。这是我们在所有实验中使用的框架，我们只改变了使用NSGA-II或SPEA2计算个体适应度的方式，分别在公式2或3中正式定义。

两个种群(父代和子代)在每一代都是联合的。从这个整体种群中选择最好的个体复制到存档种群中，该种群包含与原始种群相同数量的个体。然后存档种群作为下一代的父代种群。存档种群在整个进化过程中提供了保持非支配解集的精英策略。

4. Semantic-based MOGP Methods

接下来，我们介绍本文使用的基于语义的方法，这些方法被纳入到基线MOGP算法中，即NSGA-II和SPEA-2。

4.1. Semantic Similarity-based Crossover MOGP

我们考虑在MOGP中融入语义的第一种方法是Uy等[8]针对单目标遗传规划提出的基于语义相似度的交叉(SSC)。

SSC要求语义距离。该距离被计算为父代和子代之间每一个$in\in I$ (或部分输入集合)的绝对值之差的平均值。当距离值落在一个特定的范围内时，由一个或两个边界定义，通过交叉的方式产生后代。考虑到这可能很难满足，原始方法通过重复交叉鼓励多样性，最多20次尝试。如果不满足条件，则按常规执行交叉操作。

SSC是对GP的一个显著贡献，因为它表明在连续的搜索空间中促进语义多样性是可行的，这导致了后续的一些研究[2、31、32、33、34]。在这项工作中，我们实现了文献[8]中提出的SSC，但首次将该方法作为MOGP框架的一部分，使用NSGA-II和SPEA2作为基线算法。我们在第6节讨论的结果表明，与单目标GP不同，MOGP SSC并没有带来显著的性能提升。

4.2. Semantic-based Crowding Distance

在基于语义拥挤距离(SCD)中，关键要素是定义一个个体(枢纽)，该个体(枢纽)可用于计算该个体与群体中某些要素之间的语义距离。算法2展示了SCD MOGP的工作原理。它利用父代种群$P_t$和子代种群$Q_t$的非支配排序解创建一个新的种群$P_{t+1}$，并将其合并为种群$R_t$(第2-3行)。直到$P_{t+1}$的尺寸与$P_t$(第4-12行)的尺寸相等。这可能是一个特定的锋面不完全适合新的种群，并且需要第二个标准来完成$P_{t+1}$。如果是这种情况，我们继续存储($F_r$)，剩下的那些没有被用来完成种群(第13-24行)的个体。然后我们使用语义距离作为标准从$F_r$中选择那些点来完成$P_{t+1}$。为此，我们使用拥挤距离寻找一个支点$v$，它是距离第一前沿最远的点，解释在3.2.1 (第15-16行)节。图1中的虚线红色矩形说明了如何从第1个前方选择支点(红点)。

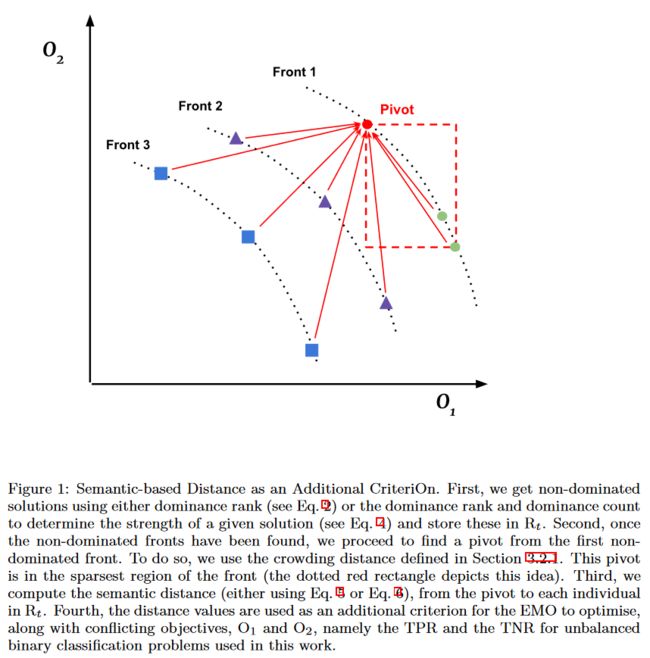
• 图1：基于语义的距离作为附加标准。首先，我们使用支配等级(见Eq.2 )或者支配等级和支配计数来确定给定解(见Eq.4 )的强度并将其存储在$R_t$中，得到非支配解。其次，一旦找到了非支配前沿，我们继续从第一个非支配前沿中寻找支点。为此，我们使用3.2.1节中定义的拥挤距离。该支点位于前方(点状红色矩形刻画了这一思想)最稀疏的区域。第三，我们计算了从枢轴到Rt中每个个体的语义距离(要么使用公式5或式6 )。第四，将距离值作为EMO优化的附加准则，并结合相互冲突的目标$O_1$和$O_2$，即本文所使用的非平衡二分类问题的TPR和TNR。

计算$F_r$中每个点与枢轴的语义距离(第17行)。因此，计算这个距离只需要一个枢轴。形式上，该距离的计算公式为(5)：

其中$p_j$是$R_t$中的个体，$l$是适应度案例的数量，LBSS和UBSS分别是语义相似度值的下界和上界。最后两个值用于促进一定范围内的语义多样性，正如文献[8]所报道的那样。

也有多项研究得出只有一个边界是必要的，以促进语义多样性[2、3、22]。我们可以用下面公式(6)的距离来计算枢轴$v$和$R_t$中每个个体之间的语义距离:

然后利用存储的$F_r$ (Line 18)上的语义距离值，选择搜索空间中稀疏区域的个体，直到完成$P_{t+1}$ (第20-23行)。

4.3. Semantic-based Distance as an Additional CriteriOn

我们进一步扩展SCD，使用得到的语义距离值作为另一个指标，通过MO过程选择解决方案。我们将这种方法称为基于语义的距离(SDO)。与SSC一样，对于SDO，我们继续使用上面描述的MOGP框架。该方法在算法 3中有详细介绍。

首先，我们将父代种群$P_t$和子代种群$Q_t$合并为$R_t$。然后得到非支配排序解(第2-3行)。为了计算$R_t$中每个点的语义距离，我们做了如下工作。我们首先计算距离第一个波阵面的拥挤距离并选择距离最远的点。我们以此作为枢轴$v$来计算$v$与$R_t$ (第4-5行)中包含的每个个体之间的语义距离。然后使用得到的距离值，利用式(5) (需要两个界限值)或式(6) (一个界限值是必要的)，作为另一个待计算的准则(第6行)。接下来，我们对$R_t$ (Line 7)进行排序，形成新的种群$P_{t+1}$(第8-12行)。当$P_{t+1}\cup F[j]$的规模大于$|Pt|$时，我们只取完成$P_{t+1}$所需的个体。图1描绘了这一思路。

References

Galván E, Trujillo L, Stapleton F. Semantics in multi-objective genetic programming[J]. Applied Soft Computing, 2022, 115: 108143.