2023牛客寒假算法基础集训营1题解

A-World Final? World Cup! (I)

传送门

思路

依次遍历每个字符串，然后在加的同时判断是否已经达到题目要求的：当前双方比分已经使得无论之后的罚球结果如何都不会影响比赛的结果，达到的话直接return，没达到的话就继续遍历，如果到最后也没有达到就return -1

code

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
vector<int> v;

void solve() {
    string s;
    cin >> s;
    s = " " + s;
    int res1 = 0, res2 = 0;
    for (int i = 1; i < s.size(); i ++ ) {
        if (s[i] == '1') {
            if (i % 2) {
                res1 ++ ;
            } else {
                res2 ++ ;
            }
        }
//        cout << i << " " << res1 << " " << res2 << endl;
        int cnt1 = 0, cnt2 = 0;
        if (i % 2 == 0) {
            cnt1 = (10 - i) / 2;
            cnt2 = (10 - i) / 2;
        } else {
            cnt1 = (10 - i) / 2;
            cnt2 = (10 - i) / 2 + 1;
        }
        if (res1 > res2 + cnt2) {
            cout << i << endl;
            return;
        }
        if (res2 > res1 + cnt1) {
            cout << i << endl;
            return;
        }
    }
    cout << -1 << endl;
}

int main() {
    int t = 1;
    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

C-现在是，学术时间 (I)

传送门

思路

只需要统计引用量大于0的文章数目即可。题目里对H指数的描述很复杂，说的是：有至少H篇论文的引用量大于等于H，因为求的是总和最大值，可以先转化为有H篇论文的引用量大于等于H，所以总和的最大值应该是求所有>0的引用量的文章个数，=0的情况对答案没有加成，就不算了。

code

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
vector<int> v;
int a[N];

void solve() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ ) {
        cin >> a[i];
    }
    sort(a + 1, a + 1 + n);
    int cnt = 0;
    for (int i = 1; i <= n; i ++ ) {
        if (a[i] < i) {
            cnt = i;
            break;
        }
    }
    LL res = 0;
    res += (n - cnt);
    for (int i = 0; i <= cnt; i ++ ) {
        if (a[i]) {
            res ++ ;
        }
    }
    cout << res << endl;
}

int main() {
    int t = 1;
    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

D-现在是，学术时间 (II)

传送门

思路

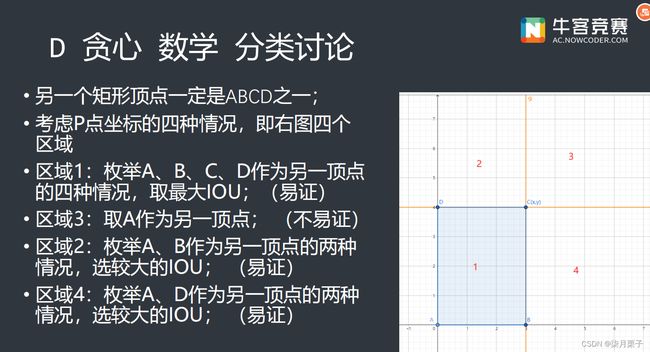
要使IOU数目最大，IOU = 交 / 并，并 = 两个面积相加 - 交，所以需要交最大。
分成四种情况：
① xp > x && yp > y
交最大面积是$x\ast y$, 并面积是$xp\ast yp$

② xp <= x && yp > y
$s1=x\ast y$
$s2=xp\ast yp$
$s3=(x-xp)\ast yp$
这个里面有两种情况 :
1)左半部分的交大，对应交面积为$xp\ast y$，并面积为$s1-交+s2$
2)右半部分的交大，对应交面积为$(x-xp)\ast y$,并面积为$s1-交+s3$

③xp > x && yp <= y
$s1=x\ast y$
$s2=xp\ast yp$
$s3=xp\ast (y-yp)$
这个里面有两种情况 :
1)下半部分的交大，对应交面积为$x\ast yp$，并面积为$s1-交+s2$
2)上半部分的交大，对应交面积为$x\ast (y-yp)$,并面积为$s1-交+s2$

④xp <= x && yp <= y
并面积是$x\ast y$
交面积有四种情况:
1)左下$xp\ast yp$
2)右下$(x-xp)\ast yp$
3)左上$xp\ast (y-yp)$
4)右上$(x-xp)\ast (y-yp)$
最后求交面积的最大值即可

code

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 400 + 10;
vector<int> v;
char g[N][10];

void solve() {
    double x, y, xp, yp;
    cin >> x >> y >> xp >> yp;
    if (xp > x && yp > y) {
        double s1 = x * y;
        double s2 = xp * yp;
        printf("%.10lf\n", s1 / s2);
    } else if (xp <= x && yp > y) {
        double s1 = x * y;
        double s2 = xp * yp;
        double s3 = (x - xp) * yp;
        double inter1 = xp * y;
        double inter2 = (x - xp) * y;
        double inter = max(inter1, inter2);
        double unionset;
//        cout << s1 << " " << s2 << " " << s3 << endl;
        if (inter == inter1) {
            unionset = s1 - inter + s2;
//             cout << ">";
        } else {
            unionset = s1 - inter + s3;
        }
//        cout << inter << " " << unionset << endl;
        printf("%.10lf\n", inter / unionset);
    } else if (xp > x && yp <= y) {
        double s1 = x * y;
        double s2 = xp * yp;
        double s3 = xp * (y - yp);
        double inter1 = x * yp;
        double inter2 = x * (y - yp);
        double inter = max(inter1, inter2);
        double unionset;
        if (inter == inter1) {
            unionset = s1 - inter + s2;
        } else {
            unionset = s1 - inter + s3;
        }
        printf("%.10lf\n", inter / unionset);
    } else if (xp <= x && yp <= y) {
        double s1 = xp * yp;
        double s2 = (x - xp) * yp;
        double s3 = xp * (y - yp);
        double s4 = (x - xp) * (y - yp);
        double inter = max(max(s1, s2), max(s3, s4));
        double unionset = x * y;
        printf("%.10lf\n", inter / unionset);
    }
}

int main() {
    int t = 1;
    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

E- 鸡算几何

传送门

F-鸡玩炸蛋人

传送门

G-鸡格线

传送门

H-本题主要考察了DFS

传送门

思路

开始看这个题的时候受题目影响想了DFS，因为数据范围也不大，但是想不出来咋搞，后面写了会别的又回来想，发现可以转化为 面积固定是$n\ast n\ast 10$，分别计算已知的每个小块面积是多少，最后相减即可。

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 400 + 10;
vector<int> v;
char g[N][10];

void solve() {
    int n;
    cin >> n;
    int m = n * n - 1;
    for (int i = 0; i < m; i ++ ) {
        cin >> g[i];
    }
    int res = n * n * 10;
    for (int i = 0; i < m; i ++ ) {
        int p = 10;
        for (int j = 0; j < 4; j ++ ) {
            if (g[i][j] == '1') {
                p -- ;
            } else if (g[i][j] == '2') {
                p ++ ;
            }
        }
        res -= p;
    }
    cout << res << endl;
}

int main() {
    int t = 1;
    cin >> t;
    while (t -- ) {
        solve();
    }
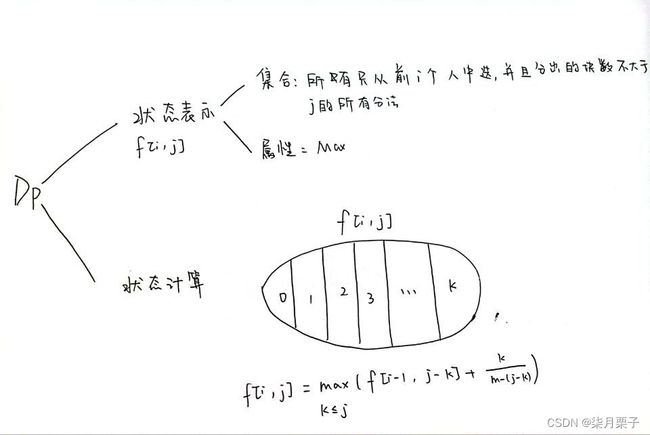
    return 0;
}

K-本题主要考察了dp

传送门

思路

分两种情况
① 0的个数小于2，坏区间是所有的区间 为 $n-2$
② 0的个数大于等于2 观察可以得出形似100100100的序列就没有坏区间（类似玄学），然后就可以构造这样的序列，100共有cnt个，前$cnt-1$个都不是坏区间，从第cnt个区间到最后依次遍历看区间的好坏

code

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 400 + 10;
vector<int> v;
char g[N][10];

void solve() {
    int n, m;
    cin >> n >> m;
    int p = n - m;
    if (p < 2) {
        cout << n - 2 << endl;
        return;
    }
    string s = "";
    int cnt = 0;
    for (int i = 1; i <= m; i ++ ) {
        s += "1";
        if (p >= 2) {
            s += "00";
            cnt ++ ;
            p -= 2;
        } else if (p == 1) {
            s += "0";
            p --;
        }
    }
//    cout << cnt << endl;
//    cout << s << endl;
    int c = (cnt - 1) * 3;
    int res = 0;
    for (int i = c; i <= n - 3; i ++ ) {
        int tmp = 0;
        if (s[i] == '1') {
            tmp ++ ;
        }
        if (s[i + 1] == '1') {
            tmp ++ ;
        }
        if (s[i + 2] == '1') {
            tmp ++ ;
        }
        if (tmp >= 2) {
            res ++ ;
        }
    }
    cout << res << endl;
}

int main() {
    int t = 1;
//    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

L-本题主要考察了运气

传送门

思路

概率题

期望 = 猜团期望 + 猜人期望 = $(1\ast 0.2+2\ast 0.2+3\ast 0.2+4\ast 0.4)+1\ast 0.25+2\ast 0.25+3\ast 0.5$ = $5.5$
由$3.45+0.05\ast i=5.5$ 得 $i=32$

code

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
vector<int> v;

void solve() {
    int i = 32;
    cout << i;
}

int main() {
    int t = 1;
//     cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

M-本题主要考察了找规律

传送门

思路

code

#include 
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 500 + 10;
vector<int> v;
double f[N][N];

void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 0; j <= m; j ++ ) {
            for (int k = 0; k <= j; k ++ ) {
                f[i][j] = max(f[i][j], f[i - 1][j - k] + (double)k / (m - j + k));
            }
        }
    }
    printf("%.10lf", f[n][m]);
}

int main() {
    int t = 1;
//     cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

赛况

除了L其他wa的次数比较少，但是做题速度也比较满，分类讨论还是不太会分

待补的题：EFG