TensorFlow入门
TensorFlow入门(二)
一、预备知识
1、tf.where(condition=seq, x=A, y=B, name=None)函数实现了选择的功能。该函数有3个参数,第一个为选择条件根据,是一个bool型的张量。当张量某一位置为True时,函数会返回第二个参数中相同位置的处的值,否则会返回第三个参数中相同位置处的值,最终返回与seq维度相同的张量。
2、tf.greater(a, b)函数的输入是两个维度相同的张量,此函数会比较第一个输入张量和第二个输入张量中相同位置处每一个元素的大小,如果在该位置第一个输入张量的元素大于第二个输入张量的元素,则函数返回True,否则为False。
以上两种函数经常一起使用,代码如下:
a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b) # 若a>b,返回a对应位置的元素,否则返回b对应位置的元素
print(c) # tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)
3、np.random.RandomState.rand(维度)函数,返回[0, 1)之间的随机数,维度为空就返回标量。
rdm = np.random.RandomState(seed=1) # 设置种子,使每次产生的随机数相同
a = rdm.rand()
b = rdm.rand(2, 3)
print(a) # 0.417022004702574
print(b)
# [[7.20324493e-01 1.14374817e-04 3.02332573e-01]
# [1.46755891e-01 9.23385948e-02 1.86260211e-01]]
4、np.vstack(数组1, 数组2)函数,将两个数组按照垂直方向叠加。
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.vstack((a, b)) # 必须加括号
print(c)
# [[1 2 3]
# [4 5 6]]
5、np.mgrid[]函数、.ravel()函数、np.c_[]函数经常一起使用。
np.mgrid[起始值: 结束值: 步长, 起始值: 结束值: 步长, …],左闭右开
x.ravel()函数将x拉直成一维数组
np.c_[数组1, 数组2, …]使返回的间隔数值点配对
三个函数配对使用用于生成网格坐标点
针对np.mgrid[]函数:当型如np.mgrid[a: b: c, d: e: f]时,维度为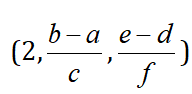
分为两块,第一块每一行的数值相同,逐行递增c;第二块每一列数值相同,逐列递增f。
x = np.mgrid[1:4:1, 2:5:0.5]
print(x)
# [[[1. 1. 1. 1. 1. 1. ]
# [2. 2. 2. 2. 2. 2. ]
# [3. 3. 3. 3. 3. 3. ]]
#
# [[2. 2.5 3. 3.5 4. 4.5]
# [2. 2.5 3. 3.5 4. 4.5]
# [2. 2.5 3. 3.5 4. 4.5]]]
针对.ravel()函数:按照维度优先级逐个元素放入一维数组。
k = np.mgrid[1:3:1, 2:3:0.5]
print(k)
# [[[1. 1. ]
# [2. 2. ]]
#
# [[2. 2.5]
# [2. 2.5]]]
print(k.ravel()) # [1. 1. 2. 2. 2. 2.5 2. 2.5]
针对np.c_[]函数,将给定数组中的每一块一一配对
a = np.array([[1, 2, 3], [2, 2, 2]])
b = np.array([[2, 4, 6], [1, 1, 1]])
print(np.c_[a, b])
# [[1 2 3 2 4 6]
# [2 2 2 1 1 1]]
c = np.array(([1, 2, 3]))
d = np.array(['one', 'two', 'three'])
print(np.c_[c, d])
# [['1' 'one']
# ['2' 'two']
# ['3' 'three']]
二、神经网络复杂度和学习率
1、NN复杂度:多用NN层数和NN参数的个数来表示。
2、空间复杂度:
层数=隐藏层的层数+1个输出层
总参数=总w+总b
3、时间复杂度:
乘加运算次数
4、指数衰减学习率:可以先用较大的学习率,快速得到较优解,然后逐步减小学习率,使模型在训练后期稳定。
指数衰减学习率=初始学习率*学习率衰减率
import tensorflow as tf
w = tf.Variable(tf.constant(5, dtype=tf.float32))
epoch = 40
LR_BASE = 0.2 # 最初学习率
LR_DECAY = 0.99 # 学习率衰减率
LR_STEP = 1 # 喂入多少轮BATCH_SIZE后,更新一次学习率
for epoch in range(epoch): # for epoch 定义顶层循环,表示对数据集循环epoch次,此例数据集数据仅有1个w,初始化时候constant赋值为5,循环100次迭代。
lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)
with tf.GradientTape() as tape: # with结构到grads框起了梯度的计算过程。
loss = tf.square(w + 1)
grads = tape.gradient(loss, w) # .gradient函数告知谁对谁求导
w.assign_sub(lr * grads) # .assign_sub 对变量做自减 即:w -= lr*grads 即 w = w - lr*grads
print("After %s epoch,w is %f,loss is %f,lr is %f" % (epoch, w.numpy(), loss, lr))
三、激活函数
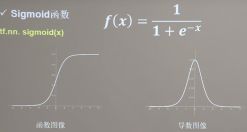
1、Sigmoid函数:tf.nn.sigmoid(x),把输入值变成0~1之间输出。如果输入值为非常大的负数,输出为0;输入值为非常大的正数,输出为1。
由于深层神经网络更新参数时,需要从输出层到输入层逐层进行链式求导,而Sigmoid函数导数为0~0.25之间的小数,会造成梯度消失。我们希望输入每层神经网络的特征是以0为均值的小数值,而经过Sigmoid函数的输出值大于0,会造成收敛太慢。另外Sigmoid函数存在幂运算,计算复杂度大,训练时间长。
2、Tanh函数:tf.math.tanh(x),输出以0为均值,但是导数在0~1之间,容易造成梯度消失。存在幂运算,训练时间长。
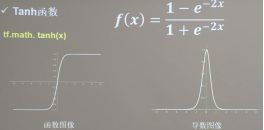
3、Relu函数:tf.nn.relu(x),解决了梯度消失问题(正区间),只需判断输入是否大于0,计算速度快,收敛速度远快于前两种激活函数。但是,输出不以0为均值,收敛慢,某些神经元可能永远无法被激活(输入为负数),导致相应参数永远不能被更新。

4、Leaky Relu函数:tf.nn.leaky_relu(x),理论上具有Relu的所有优点,且不会有神经元死亡现象,但又不是总好于Relu
5、★建议:
①首选Relu函数
②学习率设置较小值
③输入特征标准化,即让输入特征满足以0为均值,1为标准差的正态分布
④初始参数中心化,即让随机生成的参数满足以0为均值,

为标准差的正态分布。
四、损失函数
1、均方误差损失函数mse:tf.reduce_mean(tf.square(y-y_))
预测酸奶日销量y,x1、x2是影响日销量的因素,建模之前应预先采集数据:每日x1、x2和y_(最佳情况:产量=销量),还要有随机噪声。
import tensorflow as tf
import numpy as np
SEED = 23455
rdm = np.random.RandomState(seed=SEED) # 生成[0,1)之间的随机数
x = rdm.rand(32, 2) # 32 x 2矩阵
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32) # 转化为张量形式,并转换数据类型
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1)) # 权重变量2 x 1
epoch = 15001
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1) # 32x2 2x1 => 32x1
loss_mse = tf.reduce_mean(tf.square(y_ - y))
grads = tape.gradient(loss_mse, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
2、自定义损失函数
import tensorflow as tf
import numpy as np
SEED = 23455
COST = 1
PROFIT = 99
rdm = np.random.RandomState(SEED)
x = rdm.rand(32, 2) # 生成[0, 1)之间随机数
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 10000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))
grads = tape.gradient(loss, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
# Final w1 is: [[1.1626335]
# [1.1191947]]
# 自定义损失函数
# 酸奶成本1元, 酸奶利润99元
# 成本很低,利润很高,人们希望多预测些,生成模型系数大于1,往多了预测
3、交叉熵损失函数CE:表示两个概率分布之间的距离。
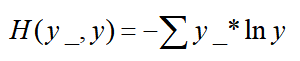
eg.二分类:已知答案y_=(1, 0),预测y1=(0.6, 0.4), y2=(0.8, 0.2),问哪一个更接近标准答案?
loss_ce1 = tf.losses.categorical_crossentropy([1, 0], [0.6, 0.4])
loss_ce2 = tf.losses.categorical_crossentropy([1, 0], [0.8, 0.2])
print(loss_ce1) # tf.Tensor(0.5108256, shape=(), dtype=float32)
print(loss_ce2) # tf.Tensor(0.22314353, shape=(), dtype=float32)
y2预测更准确
一般输出先经过tf.nn.softmax()函数,再计算y与y_的交叉熵损失函数。TensorFlow给出了两者的合并tf.nn.softmax_cross_entropy_with_logits(y_, y)
y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)
print('分步计算的结果:\n', loss_ce1)
# tf.Tensor(
# [1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00
# 5.49852354e-02], shape=(5,), dtype=float64)
print('结合计算的结果:\n', loss_ce2)
# tf.Tensor(
# [1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00
# 5.49852354e-02], shape=(5,), dtype=float64)
五、缓解过拟合
五、缓解过拟合
1、欠拟合:模型不能有效拟合数据集,是对现有数据集学习的不够彻底。
2、过拟合:模型对当前数据拟合的太好,但对从未见过的新数据难以做出 正确的判断,模型缺乏泛化力。
3、缓解欠拟合:增加特征项,给网络更多维度的输入特征,扩展网络规模;增加网络参数,提升模型表达力;减少正则化参数。
4、缓解过拟合:对数据进行清洗,减小数据集中的噪声;增加训练集;采用正则化,增大正则化参数。
5、★正则化缓解过拟合:正则化在损失函数中引入模型复杂度指标,利用给w加权值,弱化训练数据的噪声(一般不对偏置项b进行正则化)。使用正则化后,损失函数变为两部分:loss = loss(y, y_)+REGULARIZER*loss(w),前一部分为原损失函数,后一部分为用超参数REGULARIZER给出参数w在总loss中的比例,即正则化的权重。w为需要正则化的参数。
loss(w)的计算可以使用两种方法,一种是对所有参数w的绝对值求和,另一种是对所有参数w的平方求和,分别叫做L1正则化和L2正则化。
★两种正则化选择:L1正则化会大概率使很多参数变为0,因此可以通过稀疏参数,即减少参数的数量,降低模型复杂度;L2正则化会使参数接近0而不等于0,因此可以减小参数数值,有效缓解因噪声引起的过拟合。
六、神经网络参数优化器
1、待优化参数w,总损失函数loss,学习率lr,每次迭代一个batch(每个batch通常包含2的n次方组数据),t表示当前batch迭代的总次数。
2、更新参数需要四步:

其中一阶动量为与梯度相关的函数,二阶动量为与梯度平方相关的函数。不同的优化器实质上只是定义了不同的一阶动量和二阶动量公式。
3、SGD优化器(随机梯度下降): 常用的梯度下降法。
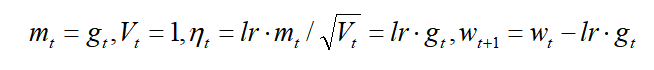
4、SGDM(在SGD基础上增加了一阶动量):

5、Adagrad(在SGD基础上增加二阶动量):

6、RMSProp(SGD基础上增加二阶动量):

7、Adam(同时结合SGDM一阶动量和RMSProp二阶动量):
