算法1—递归实现二叉树的前序、中序、后序遍历
为什么会有这三种遍历?
仅个人理解,计算机特点就是处理速度级快,为了不遗漏、不重复处理二叉树的每一个节点,总得按照某种顺序吧,前辈们发明了处理二叉树节点的顺序:前序遍历、中序遍历、后续遍历,经过时间的检验还是可以的。
二叉树的前序、中序、后序遍历的作用都是不遗漏且不重复地处理二叉树的每一个结点
理解前序、中序、后序遍历
前序
前序就是和构建二叉树一个顺序,先根节点、后左节点、最后右节点,如下图示:得到的遍历结果为:ABCDEF
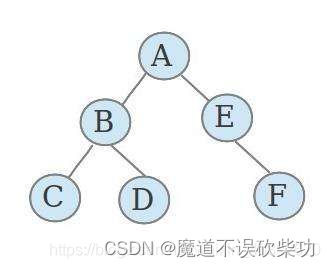
中序
中序遍历:先左节点、然后根节点、最后右节点,如下图示:得到的遍历结果为:CBDAEF
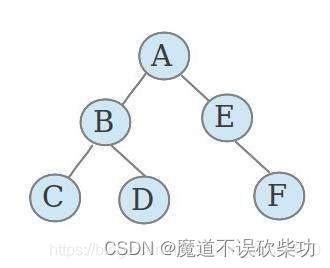
后序
后序遍历:先左节点、然后右节点、最后跟节点,如下图示:得到的遍历结果为:CDBFEA
应用场景
前序对应快排、回溯、深搜等等算法,中序对应对应汉诺塔、BST的判定等等算法,后序对应归并、堆排序、记忆搜索等等算法,各种算法模板之间是有联系的
代码实现
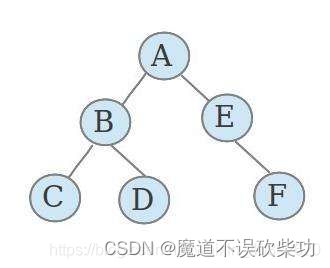
1、先构建一颗如下图所示的二叉树
定义一个 TrNode 用于封装左右指针、和 value 值
class TrNode {
public TrNode left;
public TrNode right;
public String value;
public TrNode(TrNode left, TrNode right, String value) {
this.left = left;
this.right = right;
this.value = value;
}
}
然后直接用最简单最暴力的方式构建二叉树,如下所示:
private static TrNode buildBtree() {
TrNode node_C = new TrNode(null,null,"C");
TrNode node_D = new TrNode(null,null,"D");
TrNode node_B = new TrNode(node_C,node_D,"B");
TrNode node_F = new TrNode(null,null,"F");
TrNode node_E = new TrNode(null,node_F,"E");
TrNode rootNode = new TrNode(node_B,node_E,"A");
return rootNode;
}
3、开始前序遍历二叉树代码演示:
基本思路——递归思想
- 退出条件:遍历到当前节点为 null 的时候退出这次递归调用
- 入参和返回值:入参从 root 开始,然后到他的左子右子树,返回值这里不需要,还有可以定义一个入参用于接收返回值,也可以直接使用 ThreadLocal 也可以,反正就是一个容器就行
- 处理逻辑:这里我们就直接去根节点的值作为返回结果
4、前序遍历代码演示:
public class PreOrderDemo {
public static void main(String[] args) {
TrNode rootNode = buildBtree();
List<String> result = new ArrayList<>();
preorder(rootNode,result);
System.out.println("result = " + result);
}
private static TrNode buildBtree() {
TrNode node_C = new TrNode(null,null,"C");
TrNode node_D = new TrNode(null,null,"D");
TrNode node_B = new TrNode(node_C,node_D,"B");
TrNode node_F = new TrNode(null,null,"F");
TrNode node_E = new TrNode(null,node_F,"E");
TrNode rootNode = new TrNode(node_B,node_E,"A");
return rootNode;
}
private static void preorder(TrNode curNode, List<String> result) {
// 递归退出条件
if (curNode == null) {
return;
}
// 填充本次递归调用的处理结果
fillResult(result,curNode.value);
// 递归遍历左子节点
preorder(curNode.right,result);
// 递归遍历右子节点
preorder(curNode.left, result);
}
// 就是封装跟节点值
private static void fillResult(List<String> result, String value) {
result.add(value);
}
}
输出结果所示:
result = [A, E, F, B, D, C]
Process finished with exit code 0
5、中序遍历代码演示:
public class PreOrderDemo {
public static void main(String[] args) {
TrNode rootNode = buildBtree();
List<String> result = new ArrayList<>();
preorder(rootNode,result);
System.out.println("result = " + result);
}
private static TrNode buildBtree() {
TrNode node_C = new TrNode(null,null,"C");
TrNode node_D = new TrNode(null,null,"D");
TrNode node_B = new TrNode(node_C,node_D,"B");
TrNode node_F = new TrNode(null,null,"F");
TrNode node_E = new TrNode(null,node_F,"E");
TrNode rootNode = new TrNode(node_B,node_E,"A");
return rootNode;
}
private static void preorder(TrNode curNode, List<String> result) {
if (curNode == null) {
return;
}
preorder(curNode.left, result);
// 只是这里不一样,其他都是一模一样
fillResult(result,curNode.value);
preorder(curNode.right,result);
}
private static void fillResult(List<String> result, String value) {
result.add(value);
}
}
输出结果所示:
result = [C, B, D, A, E, F]
Process finished with exit code 0
6、后序遍历代码演示:
public class PreOrderDemo {
public static void main(String[] args) {
TrNode rootNode = buildBtree();
List<String> result = new ArrayList<>();
preorder(rootNode,result);
System.out.println("result = " + result);
}
private static TrNode buildBtree() {
TrNode node_C = new TrNode(null,null,"C");
TrNode node_D = new TrNode(null,null,"D");
TrNode node_B = new TrNode(node_C,node_D,"B");
TrNode node_F = new TrNode(null,null,"F");
TrNode node_E = new TrNode(null,node_F,"E");
TrNode rootNode = new TrNode(node_B,node_E,"A");
return rootNode;
}
private static void preorder(TrNode curNode, List<String> result) {
if (curNode == null) {
return;
}
preorder(curNode.left, result);
preorder(curNode.right,result);
fillResult(result,curNode.value);
}
private static void fillResult(List<String> result, String value) {
result.add(value);
}
}
输出结果所示:
result = [C, D, B, F, E, A]
Process finished with exit code 0