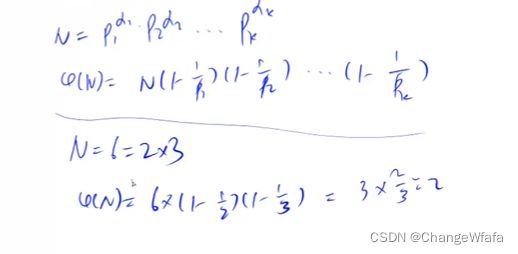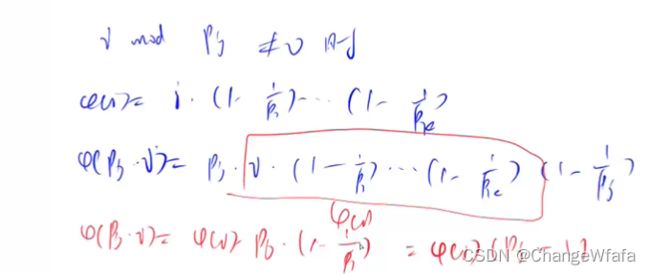算法题目总结：抓突破点的本质-解决问题

学习目的：生存的更好/卷得开心，改造环境

 将设计变现：算法逻辑实现，这就是编程的美妙之处（模板+输入输出的随机应变处理）
 学习方法：

画图，思考，应用————>提前准备好模板和应对措施就会大大提高效率（熟练掌握，能够非常快地把代码默写出来）
做题：
	1. 一定要看懂题目的前提下再做题：抓住突破点！！
	2. 先写出暴力思路，然后优化思路和实现
	3. 分解问题，解决问题

---

基础算法

二分

1. 性质：有单调性的话一定可以二分，但是二分的题目不一定必须要求单调性
2. 整数二分的本质：边界，整个区间一分为二，左满足右不满足，二分可以寻找满足性质的边界
   

两种不会错的万能板子：（整数二分）

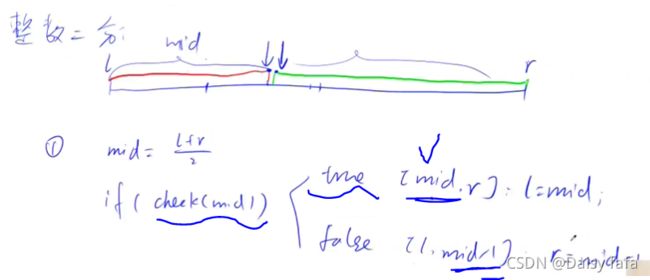
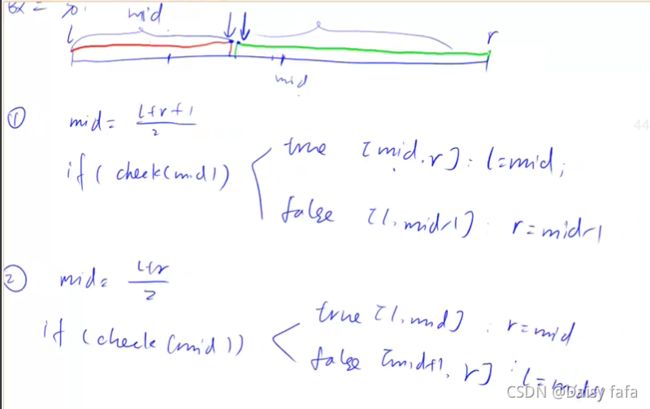
如何选择模板：

1. 先写check函数
2. 思考true和false如何更新

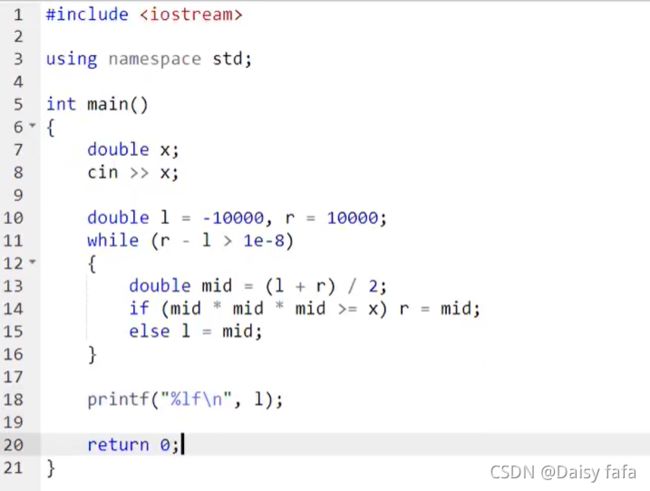
二分的主要思想：答案所在的区间（保证区间里面有答案）

3. 浮点数二分：
   输出r和l均可，因为r和l足够接近
   

前缀和与差分

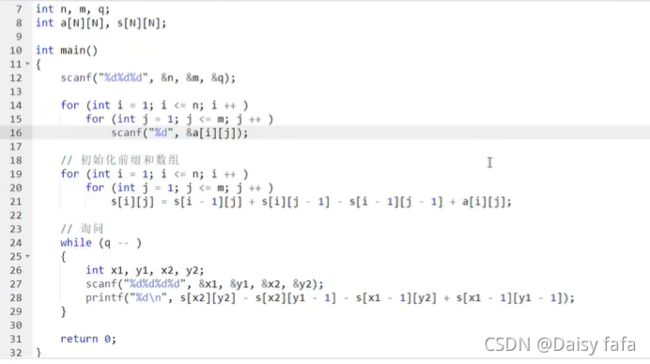
一维前缀和：
Si = a1+a2+a3+…+ai

1. 如何求Si：Si-1得到
2. 求sum[l， r]：Sr-Sl-1

二维前缀和：

差分：

1. 用处：构造差分数组，使得b数组是a数组的差分，对b数组求一遍前缀和就可以求出来原数组（O(n)）,能够使得在O(1)操作a数组中某连续区间增减固定数值
2. al-ar的区间加c：bl+c，br+1 - c

双指针

统一模板：最核心性质是将朴素的O(n^2)算法优化到O(n)
应用：输出单词，快排，KMP
思路：先思考暴力怎么写，然后看出i和j之间的单调关系，有单调关系的话利用ij之间的单调关系把时间复杂度由n^2转变成n

应用场景：

• 根据双指针唯一化数组：满足性质(a[i-1]!=a[i])，则a[j++]=a[i];

位运算操作

数字n的二进制中1的个数：n>>K&1

1. 先把第k位移到最后一位n>>k
2. 看个位是0 or 1：x&1

lowbit操作：返回x的最后一位1
x=1010，返回：10
x=101000， 返回：1000
表达式：x&-x（复数是取反加一）

区间合并算法：贪心（端点排序）

具体应用场景：快速地把有交集的区间进行合并

1. 首先根据区间左端点排序
2. 扫描，维护一个区间[st, ed]，根据下一个和当前右端点的交集关系判断

离散化：值域跨度很大，但是个数非常稀疏

1. 首先用vector对数组排序归一化（注意，已知下标数据和询问下标数据都要记录,进行离散化）
2. 离散化
   

高精度

加法，减法

设置vector，根据设置进位t，实时记录借位

乘法：大数*小数

本位：取模10
进位：除以10的数

排序算法

//基于比较的二分思想的排序算法

快速排序：分治 O(nlogn)

解决方案：确定分界点，确定左右区间（划分）
优美方法：双指针处理算法，循环迭代每次交换
背住板子，注意进入子函数后的边界问题和选择的点，避免死循环

//应用：第k个数
解决方案：快排的处理操作，单次递归
快排的每一趟，数轴的左边都会是 <= x 的， 右边都是 >= x 的。
左边元素的个数是 s1 = j - l + 1, 如果k <= s1 的话，那么下次递归的区间就是左边，否则右边。
直到 l == r 时返回q[l]。

归并排序: O(nlogn)

解决方案：以数字中间点为分界点（左右两端的二分点）划分左右区间，递归排序操作；归并操作合二为一

//应用：
求逆序对的数量
解决方案：

1. 根据中间的划分边界点利用分治思想将逆序对分成三大类，
2. 为什么能用归并板子做逆序对题目：在归并两个数组中正好根据元素所属可求出原数组逆序对数目

数据结构

//线性结构：
用数组模拟

效率：动态链表方式效率较低

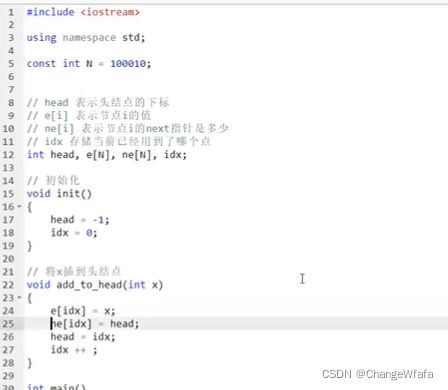
链表

数组模拟单链表：

最多的是邻接表（n个链表）：存储树和图

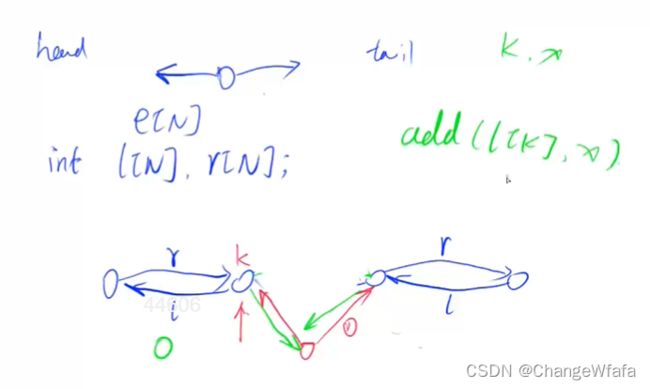
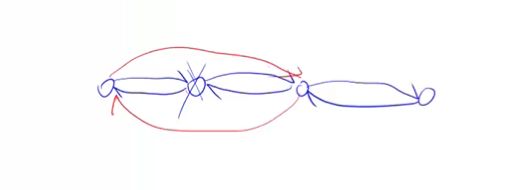
数组模拟双链表：

用来优化某些问题：每个节点有两个指针，一个指向前，一个指向后

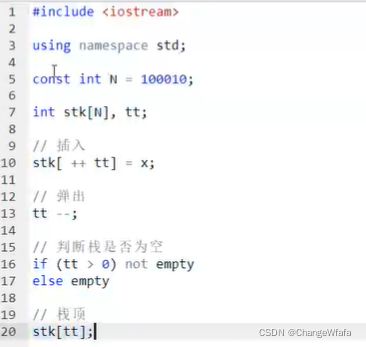
栈

数组模拟：
	栈：先进后出
	队列：先进先出

//应用：
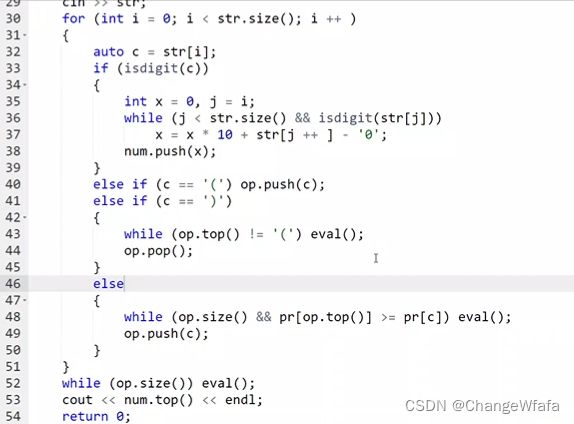
中缀表达式求值（中缀表达式树：遍历），运算顺序用栈来做
解决方案：

定义不同栈存储操作符和数字
处理初始表达式，进入不同栈，根据当前运算符和栈顶的元素选择是否操作

// 单调栈：
常见模型：给一个序列，求这个序列中某数离其左边/右边最近的最大/最小的数
解决方案：利用栈进行处理，根据单调要求，存储的是严格上升的数

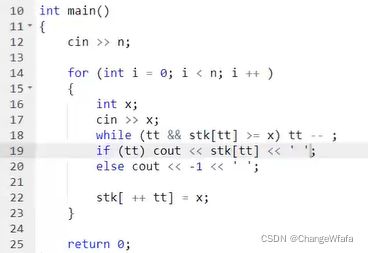
队列

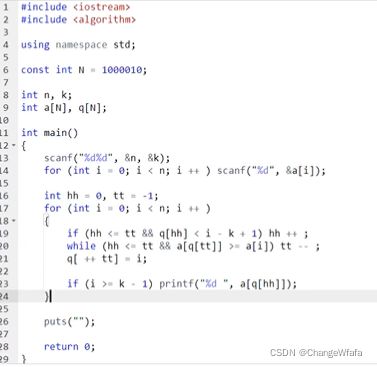
// 单调队列：滑动窗口
常见模型：求数组中滑动队列中数的最小值
解决方案：

1. 普通队列
2. 删除无用元素，使得队列具备单调性
3. 直接从模拟数组的队头/队尾O(1)取得最值

字符串

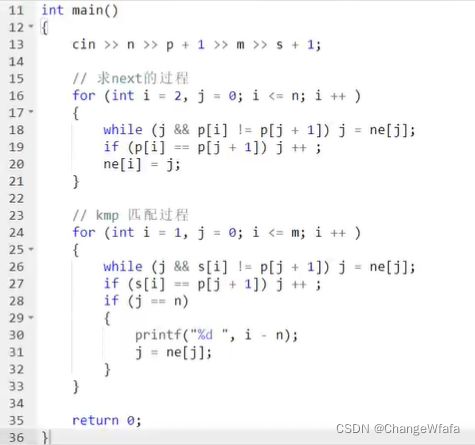
KMP

失配时：
朴素做法：O(n*m)，后移一位
KMP处理：根据预处理已匹配过的前后缀长度，利用后移数值增加 O(n)

Trie树（串树：字母类型不会很多 ）

应用：高效地存储和查找字符串集合的数据结构
问题模型：统计字符串出现频率
解决方案：

从根节点开始存储每个节点 ，每个叶节点打标记得到该字符串
根据字符串的内容创建路径/树的分支，即得串树

代码实现思路：数组模拟插入查询（多叉树）

//应用：最大异或对
问题模型：给定n个整数，从其中挑出两个整数，求最大异或值
解决方案：

优化暴力：
1. 首先将整数构造为01串，然后根据01字符串构造Trie树
2. 枚举每个数，根据Trie树查询到针对当前枚举的数找到的最大数

堆

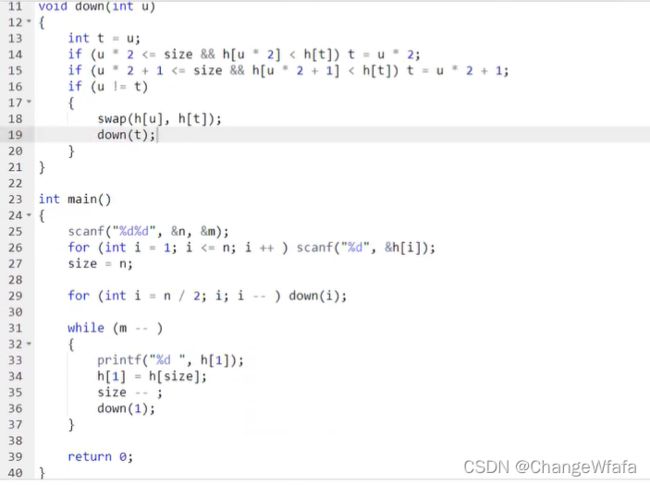
数组模拟手写实现：建堆，创建，删除
维护一个数据集合：up和down操作
1. 插入一个数
2. 求集合当中的最小值
3. 删除最小值
4. 删除任意一个元素
5. 修改任意一个元素

建堆：利用down操作的时间复杂度为O(n)

//应用-模拟堆：增加操作删去第k个元素

解决方案：
1. 增加双向映射hp（堆指向映射），ph（映射指向堆节点）
2. 增加外部映射数组，交换堆中两节点的同时交换

	首先交换蓝颜色两条边
	之后交换绿色指向边
	最后交换节点数值

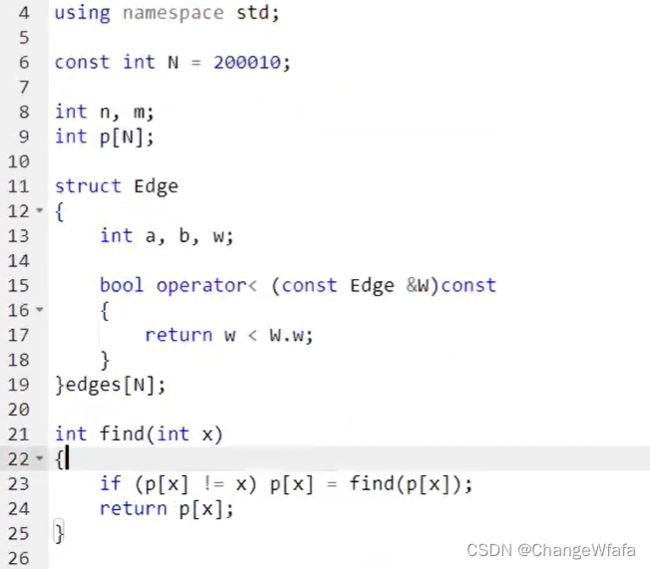
并查集：代码精简，思路精巧（思维性）

应用：快速处理集合，近乎O(1)

1. 将两个集合合并
2. 询问两个元素是否在一个集合当中

基本思想：

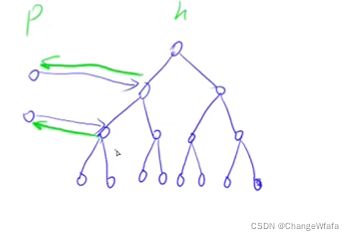
树的形式维护所有集合：每个集合用一颗树来表示，树根的编号就是整个集合的编号，每个节点存储它的父节点，p[x]表示x的父节点
问题1：如何判断树根：if(p[x] = x)
问题2：如何求x的集合编号：只要x不是树根编号，就一直往上走  while(p[x] != x) x = p[x];————>优化：路径上所有的节点都直接指向根节点，一遍即可（很好的加速-路径压缩）
问题3：如何合并两个集合：px，py分别是x，y的集合编号，让p[x]=y；

应用：图中连通块中点的数量

解决方案：集合维护连通块，维护一个size即可

应用：食物链

解决方案：判断构成环形

	并查集维护额外信息：表示同类和被吃的关系
	如何确定关系：记录每个点和根节点之间的关系，就可以知道任意两点之间的关系（判断领袖与节点的关系）
			点到根节点的距离表示关系：余1吃根节点，余2被根节点吃，余0与根节点同类
			从根节点到不同点的距离可来分析这些点的关系：不同点之间的d值模3同余的是同类

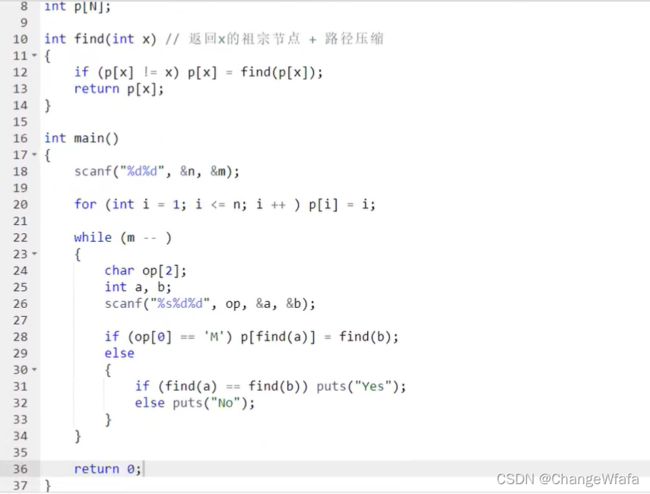
代码实现：p存储father，d存储点到根节点之间的距离（在find过程中处理）

	初始化集合
	处理关系：根据关系确定新节点的d值，处理的突破点是根据模余关系得到吃与被吃的关系

#include
#include

using namespace std;
const int N = 100010;
int p[N],d[N];

int find(int x){
    if(p[x] != x){
        int t = find(p[x]);
        d[x] += d[p[x]];   //回溯到根，在递归结束的栈顶依次处理节点到根的距离
        p[x] = t;    //节点关系路径压缩
    }
    return p[x];
}
int main(){
    int ans = 0;
    int n,m;
    scanf("%d%d",&n,&m);

    for(int i = 1;i <= n;i++)p[i] = i;   //初始化

    while(m--){
        int z,x,y;
        scanf("%d%d%d",&z,&x,&y);

        //取出x,y的两个根节点
        int px = find(x),py = find(y);

        if(x > n || y > n)ans++;
        else if(z == 1){
            //也就是说默认出现的第一个x,y都是默认正确的，只是寻找后面的x,y是否符合前面x,y的规范
            //注意只有在同一颗树的中，才能进行操作，否则将其进行加入
            //查看两个节点的距离是否模除为0 不要进行d[x] % 3 == d[y] % 3的操作 因为有可能出现负数
            if(px == py && (d[x] - d[y]) % 3 )ans++;  //在一个集合中不是同类
            else if(px != py){ //不在一个集合中，进行合并操作
                p[px] = py;
                d[px] = d[y] - d[x];
            }
        }
        else{
        //注意这里的d[x] - d[y] + 1 模3 判断，那么下面的将两个集合放在一起的操作就需要相应的减一
            if(px == py && (d[x] - d[y] + 1) % 3 )ans++;  //x不吃y说明这句话是假话
            else if(px != py){                             //若不在一个集合                     
                p[px] = py;
                d[px] = d[y] - d[x] - 1;
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

散列结构

哈希表：
	存储结构：开放寻址法，拉链法（链表存储冲突元素）
哈希函数的设置：一般情况下为模余，长度为取质数
算法操作：添加和查找某个数，打标记为删除操作

拉链法

开放寻址法

//拉链法实现

/*
 * Project: 11_哈希表
 * File Created:Sunday, January 17th 2021, 2:11:23 pm
 * Author: Bug-Free
 * Problem:AcWing 840. 模拟散列表 拉链法
 */
#include 
#include 

using namespace std;

const int N = 1e5 + 3;  // 取大于1e5的第一个质数，取质数冲突的概率最小 可以百度

//* 开一个槽 h
int h[N], e[N], ne[N], idx;  //邻接表

void insert(int x) {
    // c++中如果是负数 那他取模也是负的 所以 加N 再 %N 就一定是一个正数
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}

bool find(int x) {
    //用上面同样的 Hash函数 讲x映射到 从 0-1e5 之间的数
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i]) {
        if (e[i] == x) {
            return true;
        }
    }
    return false;
}

int n;

int main() {
    cin >> n;

    memset(h, -1, sizeof h);  //将槽先清空 空指针一般用 -1 来表示

    while (n--) {
        string op;
        int x;
        cin >> op >> x;
        if (op == "I") {
            insert(x);
        } else {
            if (find(x)) {
                puts("Yes");
            } else {
                puts("No");
            }
        }
    }
    return 0;
}

// 开放寻址法代码
/*
 * Project: 11_哈希表
 * File Created:Sunday, January 17th 2021, 4:39:01 pm
 * Author: Bug-Free
 * Problem:AcWing 840. 模拟散列表  开放寻址法
 */
#include 
#include 

using namespace std;

//开放寻址法一般开 数据范围的 2~3倍, 这样大概率就没有冲突了
const int N = 2e5 + 3;        //大于数据范围的第一个质数
const int null = 0x3f3f3f3f;  //规定空指针为 null 0x3f3f3f3f

int h[N];

int find(int x) {
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x) {
        t++;
        if (t == N) {
            t = 0;
        }
    }
    return t;  //如果这个位置是空的, 则返回的是他应该存储的位置
}

int n;

int main() {
    cin >> n;

    memset(h, 0x3f, sizeof h);  //规定空指针为 0x3f3f3f3f

    while (n--) {
        string op;
        int x;
        cin >> op >> x;
        if (op == "I") {
            h[find(x)] = x;
        } else {
            if (h[find(x)] == null) {
                puts("No");
            } else {
                puts("Yes");
            }
        }
    }
    return 0;
}

// 应用：字符串前缀哈希法

解决方案：

首先预处理所有前缀哈希
	1. 定义hash值：字符串看成p进制的数，通过取模Q把任何字符串映射到0-Q-1的数
	2. 哈希方式的选取：将字符串映射成一个数字（字符串哈希的思路）

// 字符串哈希的作用：快速判断两子串是否相同
Q: LL类型，溢出默认取模
哈希处理：h[i] = h[i-1]*p+str[i];

算法进阶

贪心

解决方案：贪心思路，尝试解决

区间问题

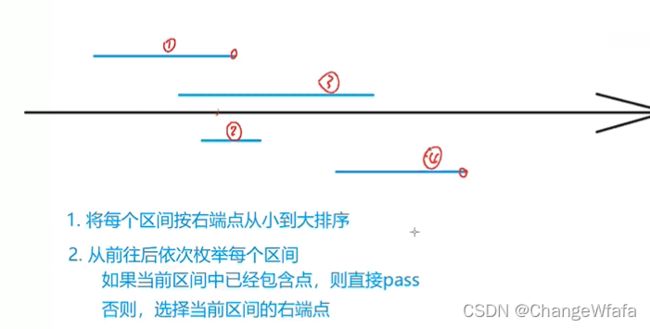
//应用：区间选点，寻找区间的交集
解决方案：

将区间排序，选择代表点，覆盖区间则pass当前区间，否则选择当前区间的右端点

// 应用：选择一组区间，是满足最大不相交区间的数量

//应用：区间分组：不相交区间分组

	给定  N  个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。输出最小组数。

// 应用：区间覆盖

	给定  N  个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。

	解决方案：将区间按照右端点从小到大排序，从覆盖起点的区间开始贪心搜索，选择覆盖范围最大的区间

// 应用：huffman编码树

	解决方案：贪心思想，利用堆（优先队列）构造Huffman树
	算法分析：堆删除和插入操作的计算量是O(logn)，总时间复杂度是O(nlogn)

#include 
#include 
#include 

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

    priority_queue<int, vector<int>, greater<int>> heap;  //初始化堆结构
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        heap.push(x);
    }

    int res = 0;
    while (heap.size() > 1)
    {
        int a = heap.top(); heap.pop(); //取出两最小节点合并
        int b = heap.top(); heap.pop();
        res += a + b;
        heap.push(a + b);
    }

    printf("%d\n", res);
    return 0;
}

//排序不等式

问题模型：排队等待打水
解决方案：从小到大排序，计算等待的最短时间

//绝对值不等式 |x-a|+|x-b|>=|a-b|

问题模型：货仓选址
解决方案：两两分组，取得最中间的那个数即可求得最小和
奇数：最中间的数进行选择
偶数：中间的前一个后一个都可选择

//推公式

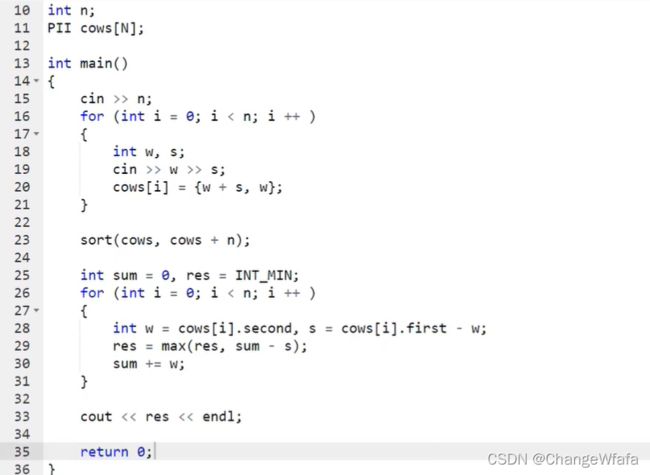
问题模型：耍杂技的牛
//一定要先审清楚题目，知道求的是什么再做题判断，不要随便解题

问题解决：
	分析：通过分析相邻两元素的危险值，得到将wi+si从大到小进行排序得到的序列结果即为最优解，因此排序求得危险值的最大值即可

搜索与图论

DFS

// 全排列

//n皇后问题

问题模型

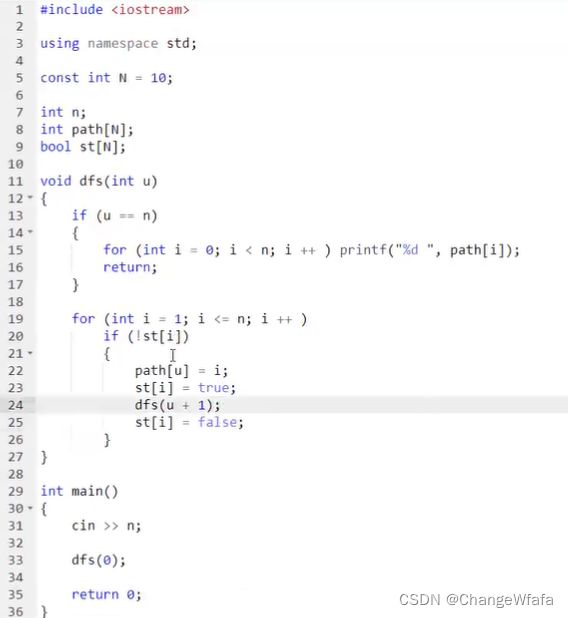
解题思路：//dfs没有模板，重要的是暴力思路和枚举顺序

两种解题效率：

1. 搜索全排列的思路：搜索顺序基本一致
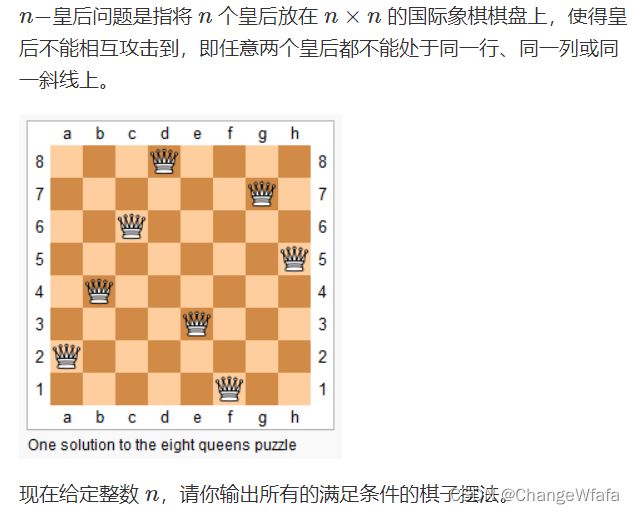
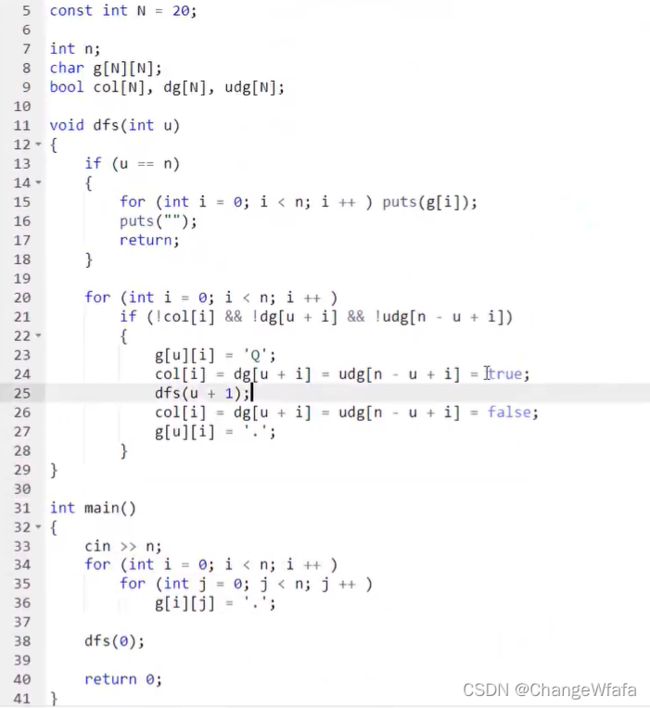
		设置对角线数组辅助记录满足条件，设置图邻接矩阵存储数据，处理过程中进行剪枝（按照行的顺序枚举）

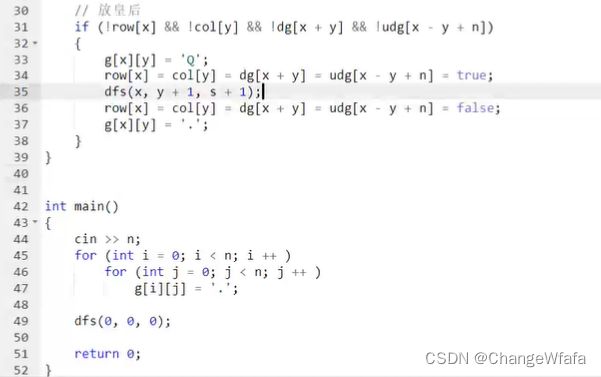
2. 枚举n^2个格子，枚举当前选择为：放或者不放

BFS

//走迷宫：兔子从窝边草开始吃

	宽搜：所有边权重相同的最短路问题

//八数码

	图中某个状态视为路径节点，从起点走到终点，BFS求最短路径
	问题：
	1. 状态表示复杂：存储方式——》字符串表示
	2. 如何记录每个状态的距离，如何做状态转移：表示状态_移动_转移状态


具体实现：距离数组存储距离，队列处理BFS

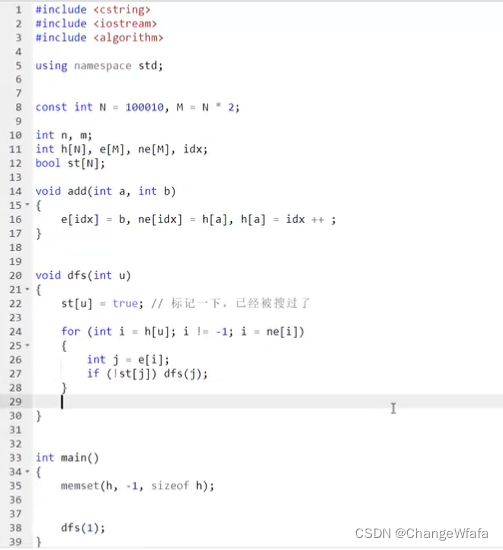
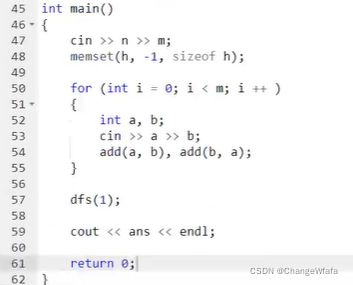
树与图的DFS

//树的重心

树与图的BFS

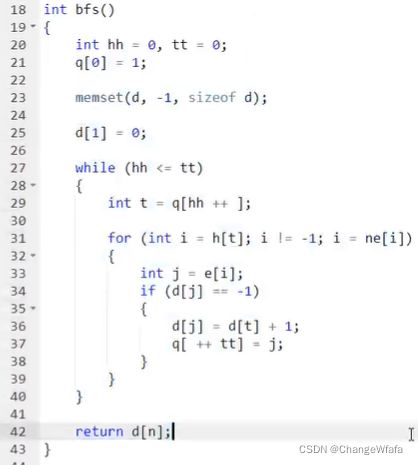
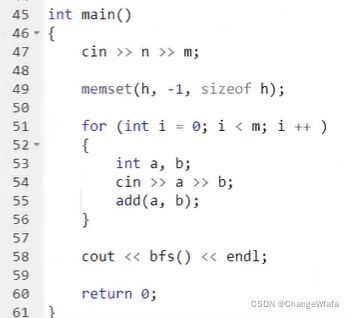
//图（权重相同为1，可用BFS求最短路径——宽搜框架搜索图）中点的层次：求图中的最短路径是否存在，存在输出

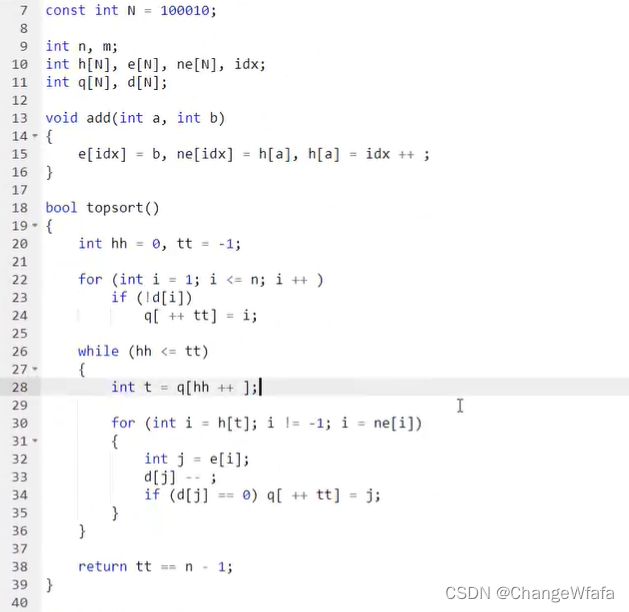
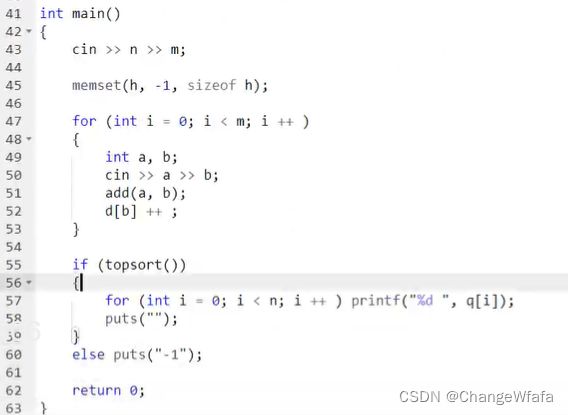
拓扑排序

//有向图的拓扑序列

解决方案：
	入度为0的点排在最前的位置
	若存在环，则一定不会入队

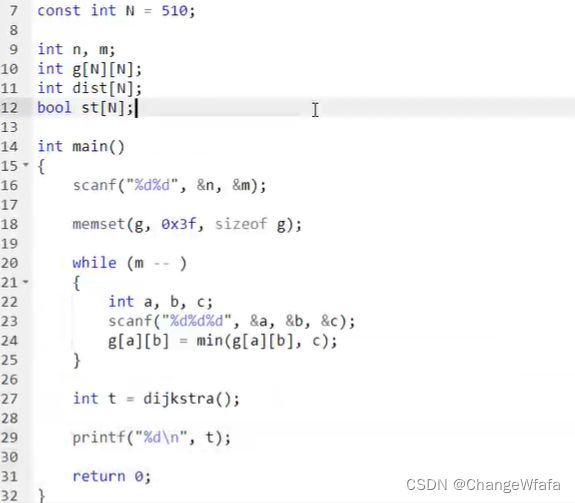
Dijkstra求最短路

//朴素dijkstra

1. 初始化初始距离
2. 迭代更新距离
		存储图：稠密-邻接矩阵，稀疏-邻接表
3. 模板（见下）

//优化dijkstra

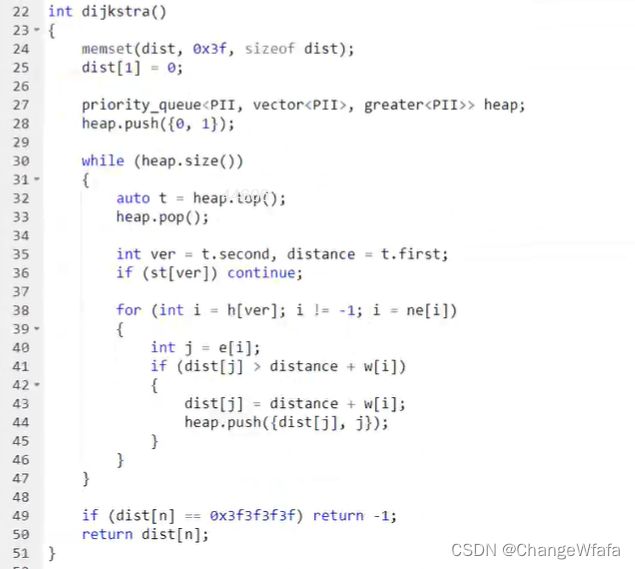
优化点：
1. 系数图：存储方式改为邻接表的方式
2. 在n次循环中，利用找到的最短距离点更新其他点的距离一共操作了m次，每次添加到堆中logn的复杂度，因此更新其他邻边节点的距离的总时间复杂度为mlogn
3. 在n次循环中，利用小根堆找到距离最近的点是O(1),所以优化到O(n)

Floyd 求最短路

应用：用来求多源最短路

	解决方案：邻接矩阵存储边
	三重循环：k从1~n，i:1~n，j:1~n
		每次更新一遍

Prim求最小生成树

//朴素版的prim算法：和dijkstra算法非常相似

Kruskal求最小生成树

//并查集的简单应用~kruskal算法

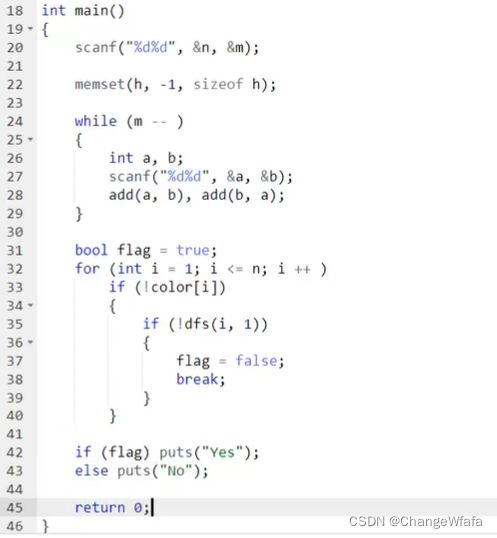
染色法：判定是否为二分图

	图论经典性质：一个图是二分图当且仅当图中不含有奇数环（环当中边的数量是奇数）
	二分图定义：根据边的邻接点的关系把所有点划分到两边集合当中，使得集合内部没有边
	解决方案：染色法判断是否为二分图

匈牙利算法：二分图的最大匹配

解决方案：
枚举左半部点，查找边，根据是否右节点已被匹配或者可更新(反悔之前的匹配)进行再次匹配，最后得到最大匹配结果

补充最短路径

//bellman-ford：有边数限制的最短路
//spfa：

• 求最短路
• 判断负环

数学知识：计算每个操作过程的时间复杂度

质数

//判定质数

判定一个数是不是质数
质数的定义：在严格大于1的整数中，如果只包含1和本身这两个约数，就被称为质数，或者叫素数

解决方案：
1. 暴力O(n)
2. 利用性质：质数都是成对出现，只枚举较小的那个即可，所以枚举到根号n即可

试除法判断质数:O(sqrt(n))

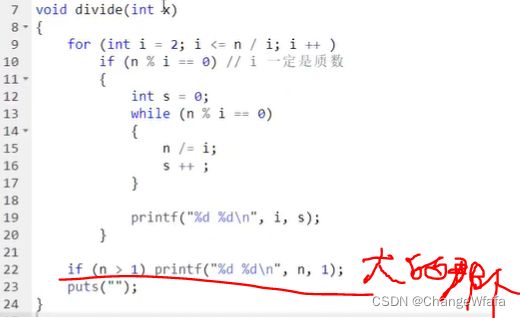
//试除分解质因数

从小到大枚举所有数
性质：n中最多只包含一个大于sqrt(n)的质因子，（反证）

//筛质数

给定一个正整数 n，请你求出 1∼n 中质数的个数
核心解决方案：根据当前以求得2-p-1中的质数的倍数筛除合数，未被筛除的p为质数（因为2-p-1中没有其质因数）

朴素筛法：枚举2-n，筛除每个i的倍数  O(nlogn)，留下质数

	优化筛除-埃式筛法：质数定理[1-n中有n/lnn个质数，O(n)一个级别]

 线性筛法：从小到大只枚举质数，筛除合数（合数是被枚举的最小的质因子筛除的）
 核心思路：
 1. n只会被最小质因子筛掉，每个数都只有一个最小质因子，所以每个数只会被筛一次，因而是线性的（pj是从小到大枚举的质数）
 2. 对于一个合数x，假设pj是x的最小质因子，当i枚举到x/pj的时候，一定会被筛掉

约数

//试除法求约数

枚举小约数，计算大约数（约数成对出现）
时间复杂度：

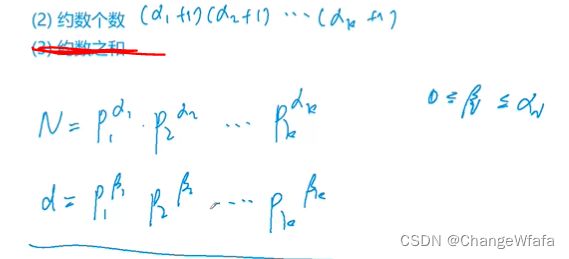
//约数个数

问题模型：给定 n 个正整数 ai，请你输出这些数的乘积的约数个数，答案对 109+7 取模
解决方案：算数公式1

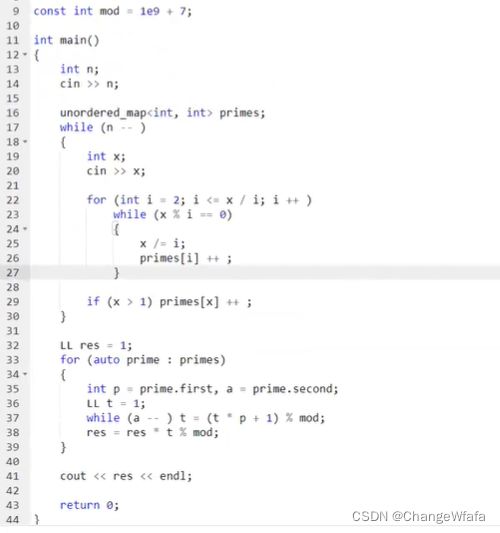
//约数之和

问题模型：给定 n 个正整数 ai，请你输出这些数的乘积的约数之和，答案对 109+7 取模
约数之和：每个括号内部选一项，根据算法分配律展开（乘积之和展开即为把所有约数加到一起）

//最大公约数/辗转相除法/欧几里得算法

欧拉函数

	解决方案：容斥原理
	利用公式定义直接求欧拉函数

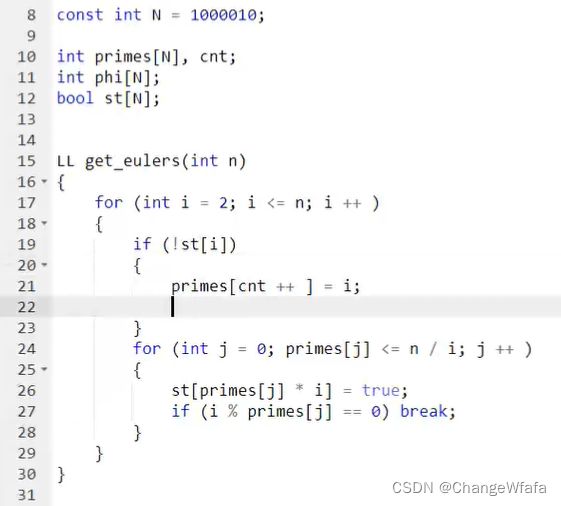
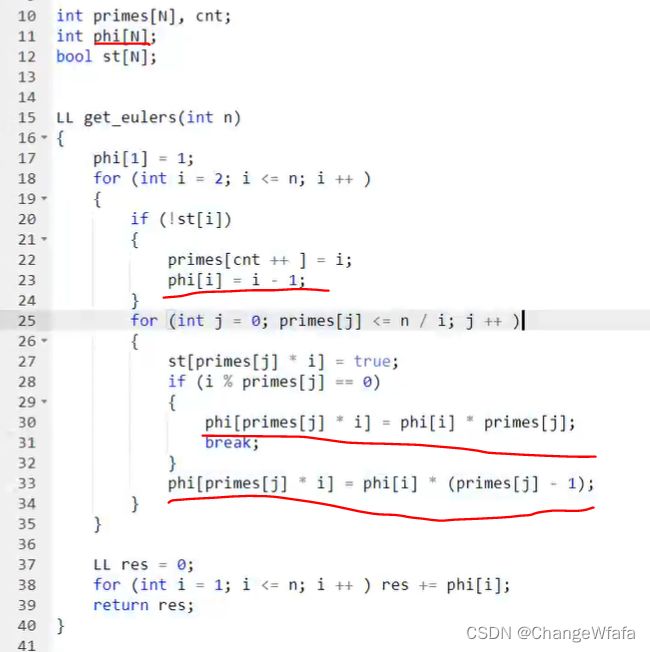
筛法求欧拉函数：O(n)复杂度求出每个数的欧拉函数

线性筛法

线性筛法求欧拉函数

快速幂

问题模型：给定 n 组 ai,bi,pi，对于每组数据，求出 ai的bi次方mod pi 的值
解决方案：反复平方法
1. 首先预处理logk个值：每个数都是上一个数的平方得到
2. 将a的k次方拆成若干个乘积的形式
3. 计算复杂度即为logk                                                                                                                                                

//快速幂求逆元

扩展欧几里得算法

	裴蜀定理：有任意正整数a, b，那么一定存在非0整数x，y使得 ax+by=gcd(a, b)    
	//求x，y的系数

//线性同余方程

 问题模型：给定 n 组数据 ai,bi,mi，对于每组数求出一个 xi，使其满足  ai  ×  xi ≡  bi  (mod  mi) ，如果无解则输出 impossible
 解决方案：b可以整除a和m的最大公约数

中国剩余定理

//表达整数的奇怪方式

高斯消元

求组合数

容斥原理

问题模型：给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个

博弈论

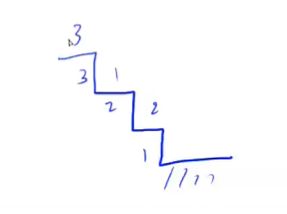
	解决方案：因为先手必须先拿some，所以可得（如下图）如果当前是全0局面，那么不管先手怎么操作，一定是非0局面；如果当前是非0局面，那么先手进行操作(拿走x使得最后为0)，一定可以得到全0局面
	核心本质：是0非0，在先后手之间来回切换

//台阶-NIM游戏

	解题方案：先手拥有必胜策略：每次挪动将奇数台阶上保持一致，最后对手先看到0----0败局，因而对手必输

//集合-NIM游戏

SG函数：状态函数（有点难，以后用了再学）

//其他游戏

动态规划：动规的本质是暴力的优化

1. 状态表示方式：化零为整，用状态表示一类问题，表示出当前所有方案
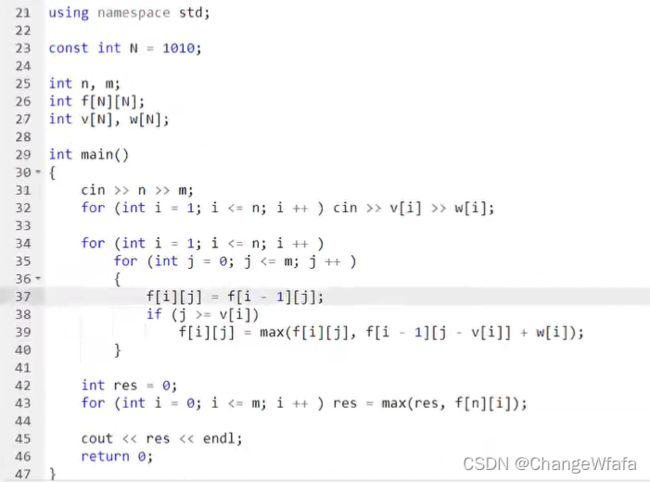
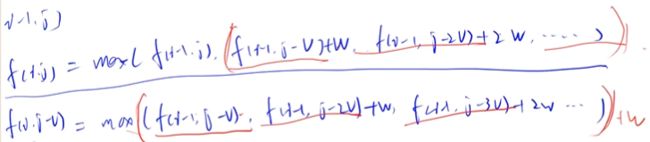
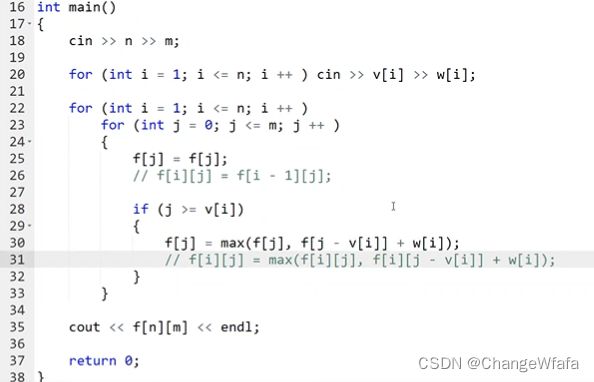
	1. 最朴素的动态规划：二维
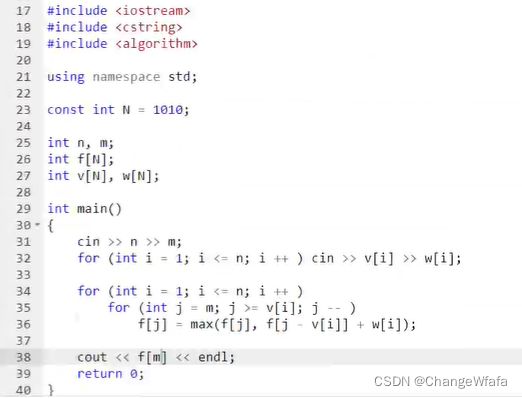
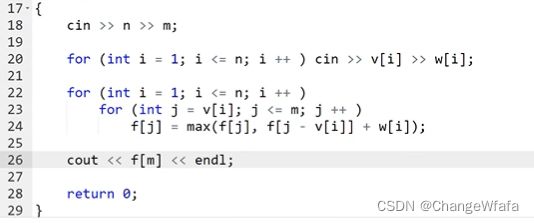
	2. 优化：一维
2. 状态计算：化整为零，状态转移计算问题（做分割，可以计算出方案之和）

背包问题

//01背包问题

滚动数组优化

//完全背包

利用性质结合滚动数组优化

//多重背包问题

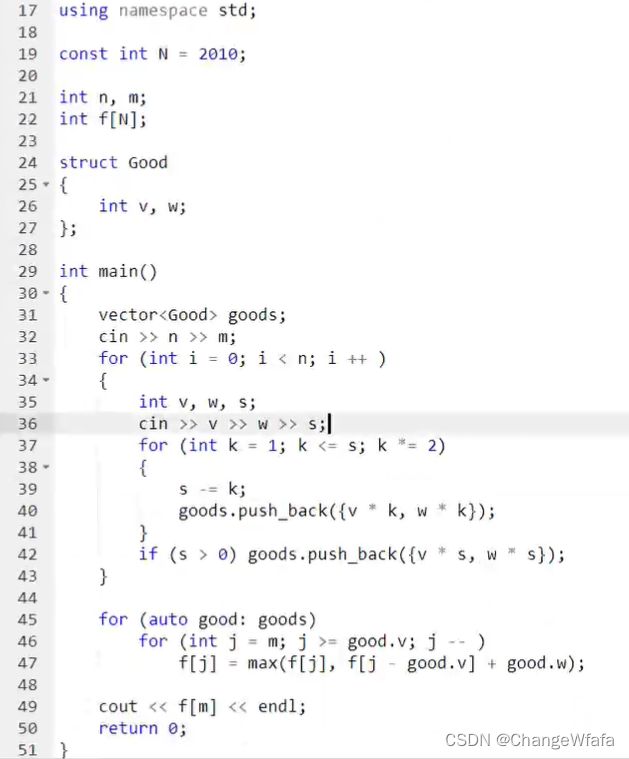
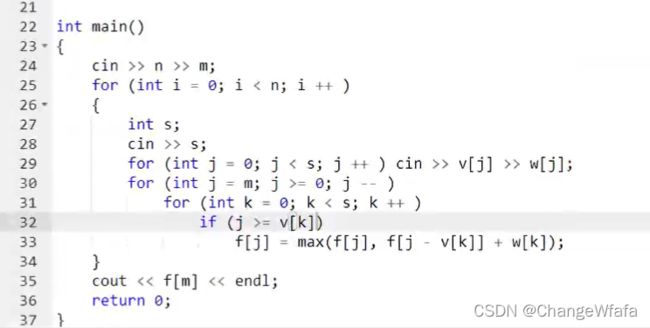
//解法2：数据范围较大，优化n^3：二进制优化方法，将S拆分成多个二进制数字累加

//分组背包

	每一组之间的物品互斥，01背包的变种
	多重背包问题是分组问题的特殊情况（0个，1个，2个打包的选择情况）

线性DP

//数字三角形

DP分析法：DP比暴搜快的原因是每次处理一类问题，暴力搜索是每次处理一个问题
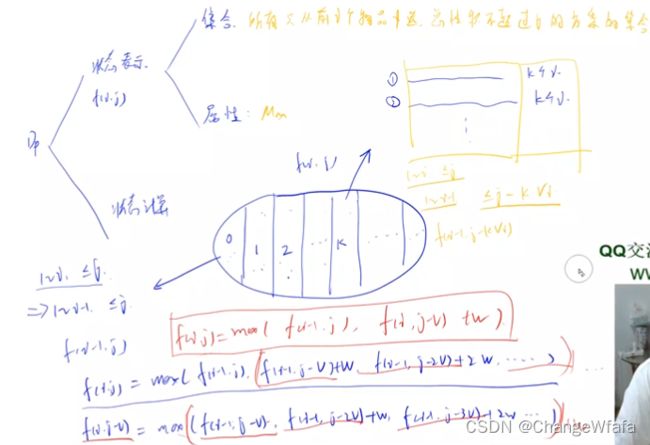
状态表示：集合，属性eg最值——(基于经验进行表示 )
状态计算：集合划分

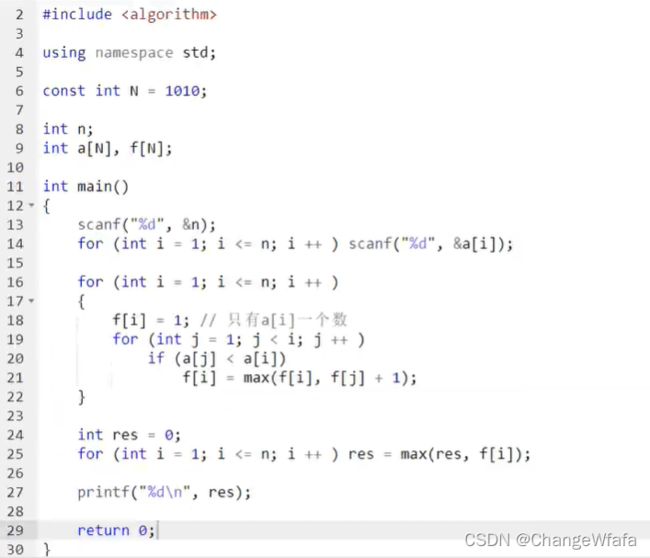
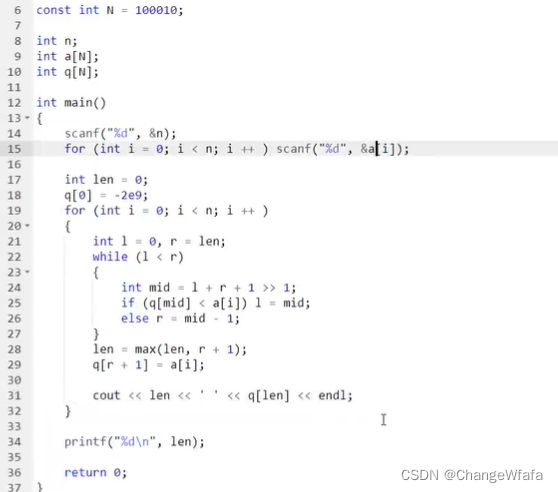
//最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少


解决方案：经典DP问题
1. 所有以i结尾的上升子序列可以分成哪些类呢？（状态计算）
2. 可以分成很多类：转换得到的先前状态

//优化：当数据更大超时候的处理

//最长公共子序列：求最长公共子序列的长度是多少

//最短编辑距离

解决方案：
分析步骤：
1. 状态表示
2. 状态计算

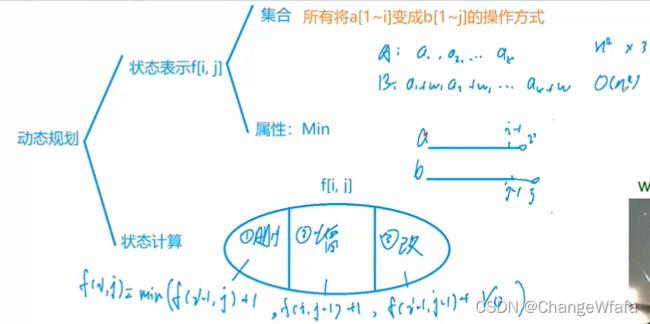
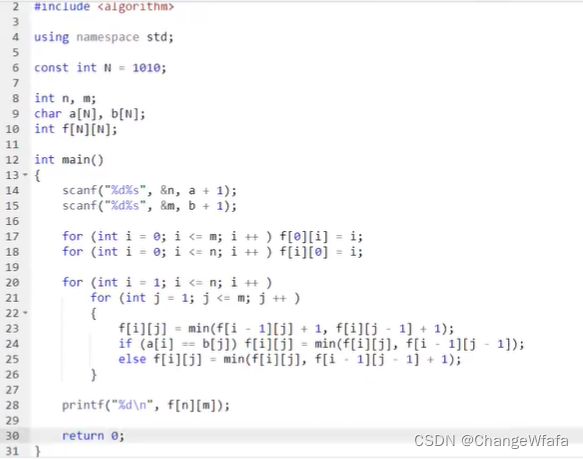
//编辑距离

	解决方案：求每个目标字符串和已有字符串的编辑距离，判断是否符合所给限制数目，最后求出问题解

区间DP

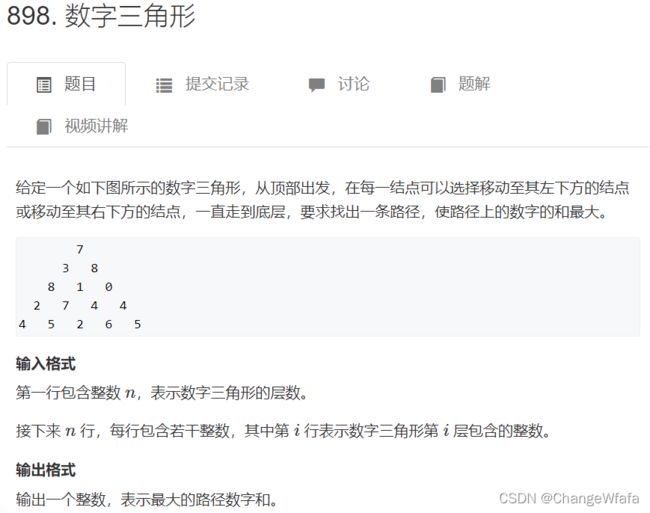
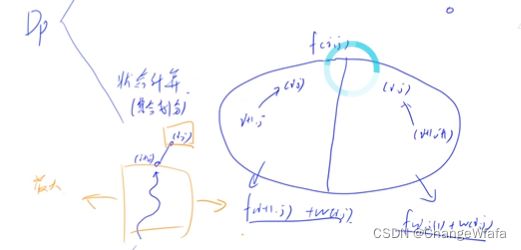
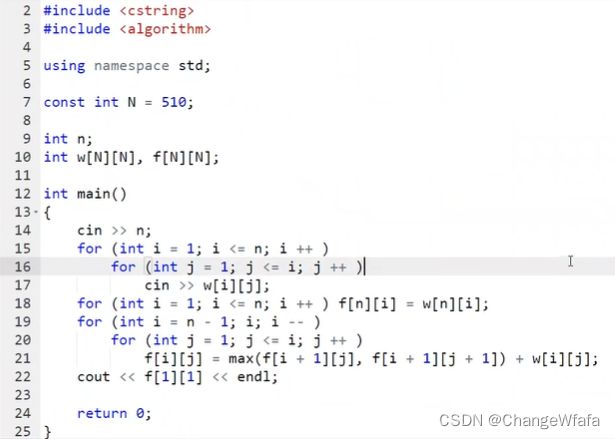
问题分析：合并相邻两堆
解决方案：
1. 状态表示：化零为整（把零散整合为一个  整体）
2. 状态计算：两区间合并，以合并临界点为标准
区间枚举套路：
	枚举区间长度
		枚举区间左端点_右端点

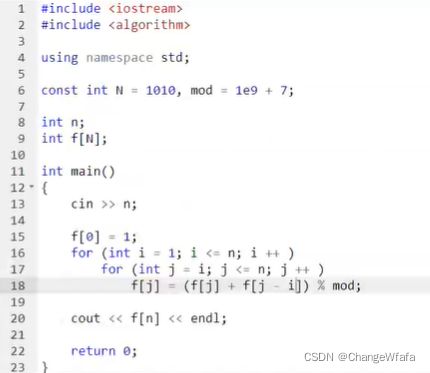
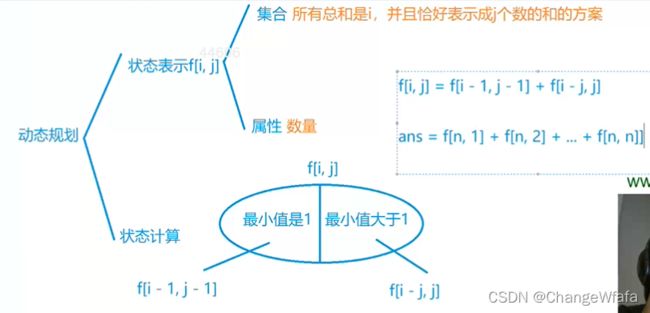
计数类DP

类似于完全背包问题的优化方式：
	找到优化方式：f[i][j] = f[i-1][j] + f[i][j-1]
	空间优化：（体积从小到大循环即可）f[j] = f[j] + f[j-1]
	本题：i是体积，j是容量
	解决方案1：变化的是选择哪些数（总和n不变）

解决方案2：最后求和才是答案（对比方案1）

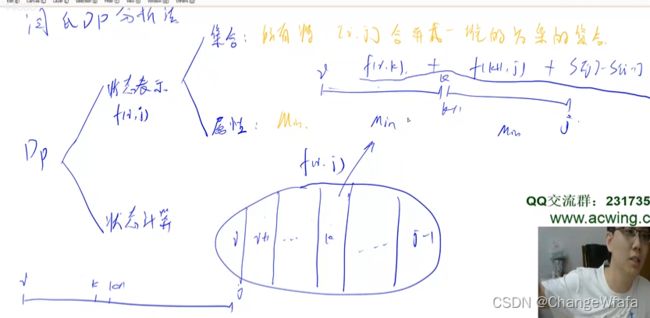
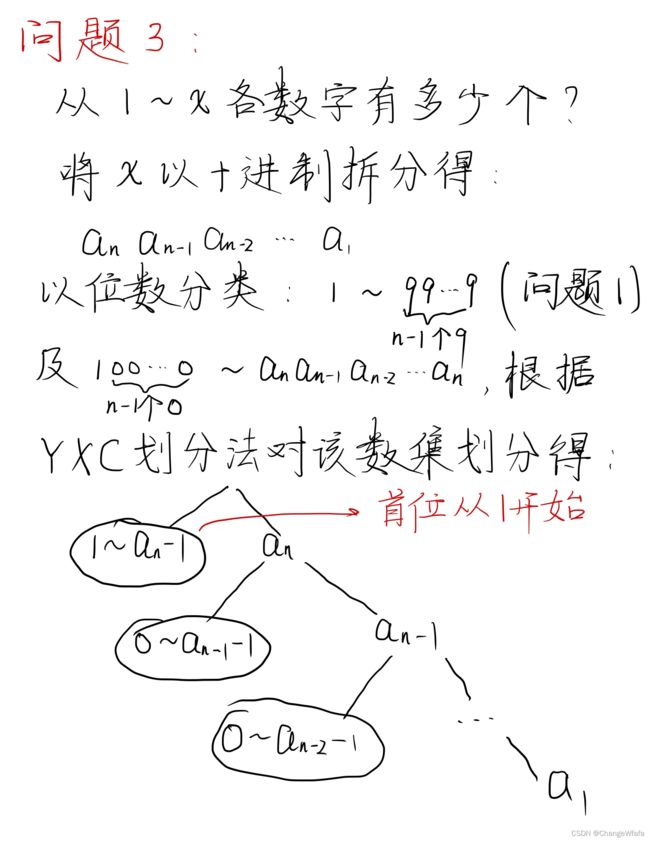
数位统计DP

解决方案：分情况讨论

//以下题解来源于acwing

#include 
#include 

using namespace std;

int base[10];
int f[10][10];
int g[10][10];

void init()
{
    base[0] = 1;
    for(int i = 1 ; i <= 9 ; i++) base[i] = base[i-1]*10;

    //从00……0 - 99……9 的各位数字有多少个，其中i为数字个数（包含前导零）
    for(int i = 0 ; i <= 9 ; i++) f[1][i] = 1;
    for(int i = 2 ; i <= 9 ; i++)
        for(int j = 0 ; j <= 9 ; j++)
            f[i][j] = f[i-1][j]*10 + base[i-1];

    //从1 - 99……9 的各位数字有多少个，其中i为数字个数（不包含前导零）
    for(int i = 1 ; i <= 9 ; i++) g[1][i] = 1;//循环从1开始
    for(int i = 2 ; i <= 9 ; i++) {
        g[i][0] = g[i-1][0] + f[i-1][0]*9;
        for(int j = 1 ; j <= 9 ; j++)
            g[i][j] = g[i-1][j] + f[i-1][j]*9 + base[i-1];
    }
}

vector<int> dp(int n)
{
    vector<int> ans(10,0); //记录答案
    if(n<=0) return ans; //边界条件

    vector<int> nums;
    while(n) nums.push_back(n%10), n/=10;

    vector<int> last(10,0); //记录前缀中各个数字个数

    //统计1 - 99……9(n-1个9)里面各个数字有多少个
    for(int i = 0 ; i <= 9 ; i++) ans[i] = g[nums.size()-1][i];
    //统计大于10……0(n-1个0) 的树里各个数字有多少个
    for(int i = nums.size()-1 ; i >=0 ; i--) {
        //循环变量i可以表示剩下的数字有多少个
        int x = nums[i];
        for(int j = i==nums.size()-1 ; j < x ; j++) { //第一次循环不能有0
            //前缀部分
            for(int k = 0 ; k <= 9 ; k++)
                ans[k] += last[k] * base[i];
            //当前位置部分
            ans[j] += base[i];
            //后缀部分
            for(int k = 0 ; k <= 9 ; k++)
                ans[k] += f[i][k];
        }
        //更新前缀计数器
        last[x] ++;

        //统计叶子节点（这个数本身）
        if(!i) for(int k = 0 ; k <= 9 ; k++) ans[k] += last[k];
    }
    return ans;
}

vector<int> ask(int a, int b)
{
    auto x = dp(b);
    auto y = dp(a-1);
    vector<int> ans;
    for(int i = 0 ; i <= 9 ; i++) ans.push_back(x[i]-y[i]);
    return ans;
}

void print(vector<int> ans)
{
    for(auto x:ans) printf("%d ",x);
    puts("");
}

bool check(int x)
{
    auto t = ask(x,x);
    vector<int> cnt(10,0);
    while(x) cnt[x%10]++,x/=10;
    for(int i = 0 ; i <= 9 ; i++)
        if(cnt[i] != t[i])
            return false;
    return true;
}

int main()
{
    init();

    //这里是一个DEBUG函数
    // for(int i = 1 ; i <= 1000000 ; i*=10) {
    //     if(!check(i))
    //         printf("ERROR:%d\n",i);
    // }

    int a,b;
    while(cin >> a >> b, a||b) {
        if(a>b) swap(a,b);
        auto t = ask(a,b);
        print(t);
    }

    return 0;
}

状态压缩DP

//蒙德里安的梦想

解决方案：

//最短Hamilton路径

解决方案：二进制01串表示状态

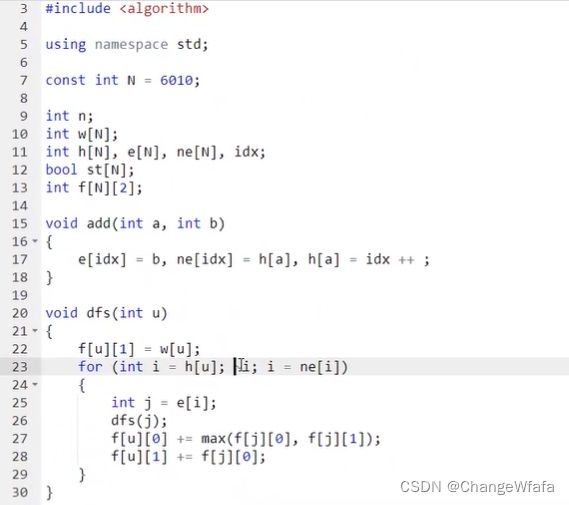
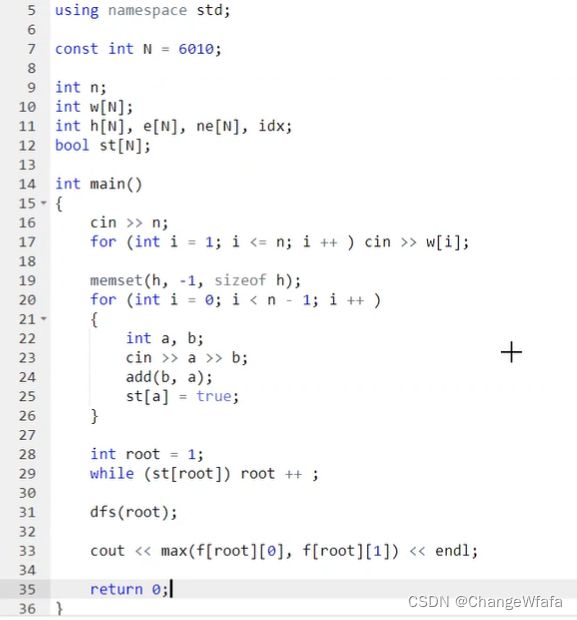
树形DP

 子树相互独立，每棵最大值之和+选根/不选根=当前根节点的最大值
 时间复杂度：O(n)

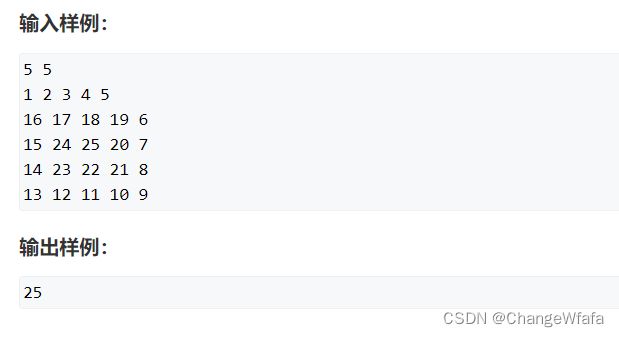
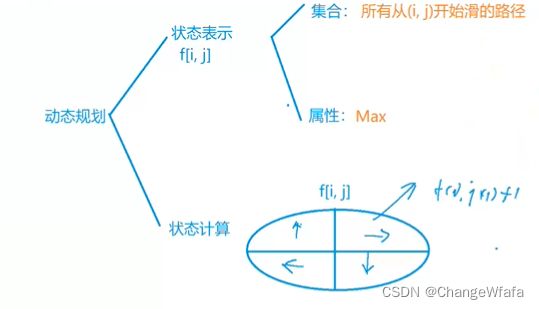
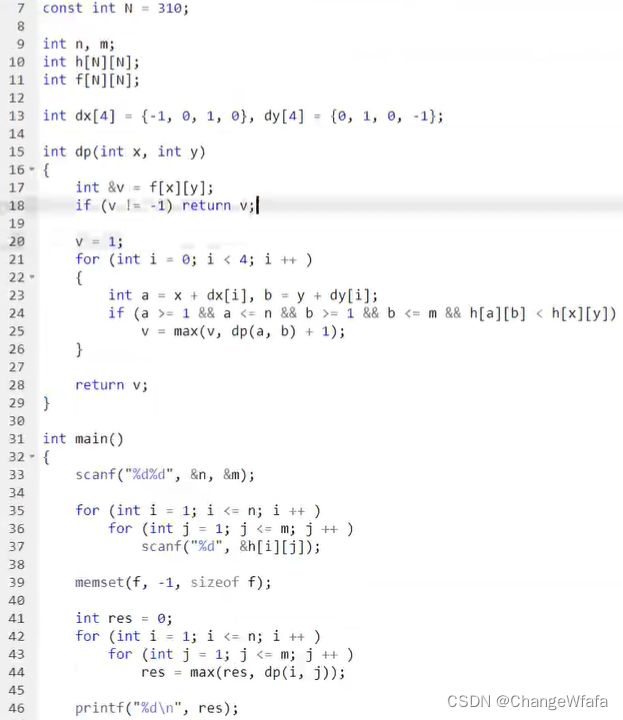
记忆化搜索

解题方案：动态规划思路
实现方式：递归-记忆化搜索

---

c++做题技巧

算法复杂度分析

• 算法优化：应用解题
• 算法设计：策略，思想
• 数学基础：级数