LeetCode刷题—岛屿问题
思路
一个二维矩阵从某个点开始向四周扩展,直到无法再扩展为止。
矩阵,可以抽象为一幅「图」,这就是⼀个图的遍历问题,也就类似⼀个 N 叉树遍历的问题。几行代码就能解决,直接上框架吧:
// (x, y) 为坐标位置
void fill(int x, int y) {
fill(x - 1, y); // 上
fill(x + 1, y); // 下
fill(x, y - 1); // 左
fill(x, y + 1); // 右
}
这个框架可以解决所有在二维矩阵中遍历的问题,说得高端点,这就叫深度优先搜索(Depth First Search,简称 DFS),说得简单点,这就叫四叉树遍历框架。坐标 (x, y) 就是 root,四个方向就是 root 的四个子节点。
DFS模板
void dfs(参数){
//dfs出口,不满足条件就退出
if(结束条件){
return;
}
操作
//递归,接着进一步DFS
dfs(...);
}
733,图像渲染,easy
有一幅以二维整数数组表示的图画,每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。
从初始坐标开始,记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。
最后返回经过上色渲染后的图像。
示例 1:
输入:
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
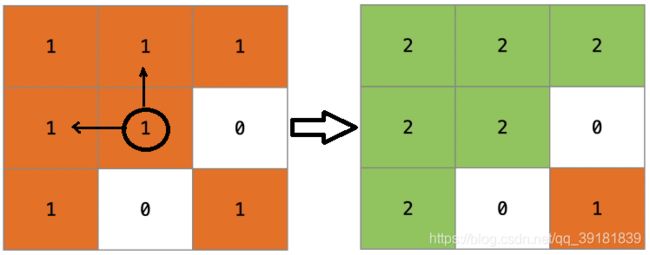
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析:
在图像的正中间,(坐标(sr,sc)=(1,1)),
在路径上所有符合条件的像素点的颜色都被更改成2。
注意,右下角的像素没有更改为2,
因为它不是在上下左右四个方向上与初始点相连的像素点。
题解
从起始点开始,搜索四个方向
-
如果这个方向越界且不需要渲染,结束搜索。
-
否则,继续从这个方向搜索它的上下左右。
代码
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
//如果新颜色与原来相同,不需更改
if(image[sr][sc] == newColor) return image;
dfs(image, sr, sc, newColor, image[sr][sc]);
return image;
}
public void dfs(int[][] image, int sr, int sc, int newColor, int oldColor){
//出口:不在合法范围内 或 此位置与初始颜色不同
if(!isValidArea(image, sr, sc) || image[sr][sc] != oldColor)
return;
//操作
image[sr][sc] = newColor;
//递归
dfs(image, sr - 1, sc, newColor, oldColor);
dfs(image, sr + 1, sc, newColor, oldColor);
dfs(image, sr, sc - 1, newColor, oldColor);
dfs(image, sr, sc + 1, newColor, oldColor);
}
//合法:不处于边界之外
public boolean isValidArea(int[][] image, int sr, int sc){
if(sr < 0 || sr >= image.length || sc < 0 || sc >= image[0].length)
return false;
return true;
}
}
200,岛屿数量,medium
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
题解
本题的目标是得到“岛屿数量”,上下左右相连的 1 都被认为是连续岛屿。
总体思路:遍历地图,找到一个陆地(’ 1 '),采用 dfs 向 上下左右 四个方向搜索,同时“岛屿数量” + 1。
dfs 流程:
-
结束条件:不在合法范围内 或 不是陆地
-
操作:避免重复遍历,网格的dfs 会重复向四个方向找,可能重复遍历节点。
将已遍历过的陆地标记为 ‘2’
-
递归:搜索上下左右的节点
代码
class Solution {
public int numIslands(char[][] grid) {
int cnt = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == '1'){
dfs(grid, i, j);
cnt++;
}
}
}
return cnt;
}
//从 一个陆地 ‘1’向四个方向遍历
public void dfs(char[][] grid, int r, int c){
if(!isValidArea(grid, r, c) || grid[r][c] != '1')
return;
//标记已遍历过的陆地
grid[r][c] = '2';
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
public boolean isValidArea(char[][] image, int sr, int sc){
if(sr < 0 || sr >= image.length || sc < 0 || sc >= image[0].length)
return false;
return true;
}
}
695,岛屿的最大面积,medium
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。
题解
和上面思路一致,根据题目对结果进行修改。
题目目标是得到最大岛屿面积,在 dfs 过程中求出每个岛屿的面积,在主函数中得到最大的一个。
代码
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == 1){
int a = dfs(grid, i, j);
res = Math.max(a, res);
}
}
}
return res;
}
public int dfs(int[][] grid, int r ,int c){
if(!isValidArea(grid, r, c) || grid[r][c] != 1)
return 0;
//标记已遍历过的陆地
grid[r][c] = 2;
return 1 + dfs(grid, r - 1, c) + dfs(grid, r + 1, c) + dfs(grid, r, c - 1) + dfs(grid, r, c + 1);
}
public boolean isValidArea(int[][] image, int sr, int sc){
if(sr < 0 || sr >= image.length || sc < 0 || sc >= image[0].length)
return false;
return true;
}
}
463,岛屿的周长,easy
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 1:
![]()
输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出:16
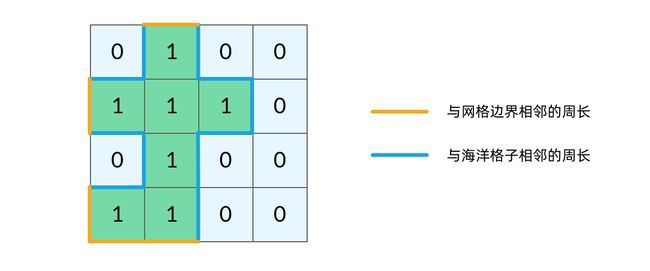
解释:它的周长是上面图片中的 16 个黄色的边
题解
岛屿的周长是计算岛屿全部的「边缘」,而这些边缘就是我们在 DFS 遍历中,dfs 函数返回的位置。
可以将岛屿的周长中的边分为两类,如下图所示。黄色的边是与网格边界相邻的周长,而蓝色的边是与海洋格子相邻的周长。
dfs 函数直接返回有这几种情况:
!inArea(grid, r, c),即坐标 (r, c) 超出了网格的范围,也就是「先污染后治理」的情况grid[r][c] != 1,即当前格子不是岛屿格子,这又分为两种情况:grid[r][c] == 0,当前格子是海洋格子grid[r][c] == 2,当前格子是已遍历的陆地格子
代码
class Solution {
public int islandPerimeter(int[][] grid) {
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == 1){
return dfs(grid, i, j);
}
}
}
return 0;
}
//从 一个陆地 ‘1’向四个方向遍历
public int dfs(int[][] grid, int r, int c){
//蓝色边界
if(!isValidArea(grid, r, c))
return 1;
//黄色边界
if(grid[r][c] == 0)
return 1;
//当前格子是已遍历的陆地格子,和周长没关系
if(grid[r][c] != 1)
return 0;
//标记已遍历过的陆地
grid[r][c] = '2';
return dfs(grid, r - 1, c) + dfs(grid, r + 1, c) + dfs(grid, r, c - 1) + dfs(grid, r, c + 1);
}
public boolean isValidArea(int[][] image, int sr, int sc){
if(sr < 0 || sr >= image.length || sc < 0 || sc >= image[0].length)
return false;
return true;
}
}
- 更简单的写法:遍历每一个空格,遇到岛屿,计算其上下左右的情况,遇到水域或者出界的情况,就可以计算边了。
class Solution {
public int islandPerimeter(int[][] grid) {
int[][] directions = {{0,1},{1,0},{0,-1},{-1,0}};
int res = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == 1){
//4个方向
for(int k = 0; k < 4; k++){
int r = i + directions[k][0];
int c = j + directions[k][1];
if(r < 0 || r >= grid.length || c < 0 || c >= grid[0].length || grid[r][c] == 0) res++;
}
}
}
}
return res;
}
}