【力扣每日一题】450. 删除二叉搜索树中的节点

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

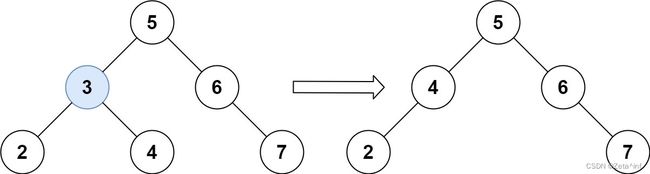
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 

另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

---

又是二叉树，还是二叉搜索树。我记得几天前刚刚在这里反思过自己的基础知识不足，没想到今天又打脸了啊。

照例看官方解法。

---

官方

官方用了两种方法，一种递归，一种迭代。

我们只分析递归，迭代的原理和递归一样，只不过实现思路不同。

这里进行了详尽的分类讨论：

先讨论当前节点是否为null，然后在root.val存在的情况下与key比较，val大于key则在左子树上继续递归，val小于key则在右子树上继续递归。

当val等于key时，这里面的情况又比较复杂了，于是又嵌套了一层分类讨论：

当前root没有左右子树时，即root为叶节点时，直接返回null，表示这个节点已经删除，没有val了；只有左/右子树时，直接返回左/右子树，表示当前root被删除，由左/右子树的root来接替。

当root的左右子树均存在时，事情变得复杂了一点，官方的解决方法是找到右子树的最小节点successor来接替root（或者找左子树的最大节点也一样 ），这个操作需要先把右子树中的那个节点successor删掉，然后再将root替换为successor，完成替换操作。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;        
        if (root.val > key)root.left = deleteNode(root.left, key);
        if (root.val < key)root.right = deleteNode(root.right, key);
        
        if (root.val == key) {
            if (root.left == null && root.right == null) return null;
            if (root.right == null)return root.left;
            if (root.left == null) return root.right;
            TreeNode successor = root.right;
            while (successor.left != null)successor = successor.left;
            root.right = deleteNode(root.right, successor.val);
            successor.right = root.right;
            successor.left = root.left;
            return successor;
        }
        return root;
    }
}

看了评论区其他大佬的解法，有些清奇的思路。

同样是构造二叉搜索树，官方的构造很中规中矩，就是代码过程的递归太多，消耗的空间比较多，也不容易读懂，但是这道题目要求的只是一个合法的BST，至于怎么排序，并没有规定，所以便有了下面的思路：

首先还是找到右子树的最小节点t，然后将root的整个左子树都接到t的左边再用右子树替代原本的root，相当于在这一部分少去了再次调用递归的过程。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val == key) {
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            TreeNode t = root.right;
            while (t.left != null) t = t.left;
            t.left = root.left;
            return root.right;
        } else if (root.val < key) root.right = deleteNode(root.right, key);
        else root.left = deleteNode(root.left, key);
        return root;
    }
}

---

今天简单理解了一下BST的删除过程，分析了两种稍微不同的解题思路。多一种思路能对知识的理解更深一层。而且删除操作也是比较实用的一种操作，以后的生活中可能会应用到这个东西。