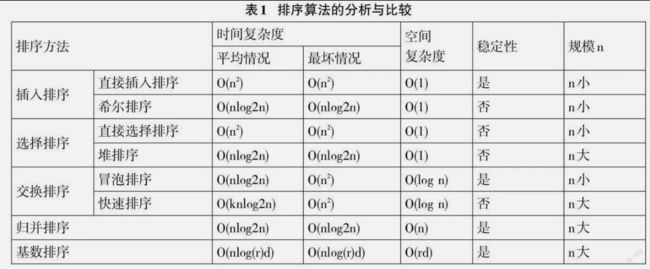
选择排序、冒泡排序、快速排序、归并排序
1、选择排序
设一个数据集有n个元素,选择这n个元素中最小的一个与第一个元素交换位置,再在剩下的n-1个元素中选择最小的一个与第二个元素交换位置,直到在最后两个元素中选择最小的一个放在倒数第二的位置上,简单选择排序是不稳定排序
f(a,n,i) 当i=n-1时:算法结束
f(a,n,i)否则:通过简单比较挑选a[i…n-1]中最小元素,a[k]放到a[i]处;f(a,n,i+1)
#include2、交换排序
2.1、冒泡排序
冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换。
#include2.2、快速排序
2.2.1、hoare(左右指针法)
2.2.2、挖坑法(递归)
时间复杂度最好情况nlogn
快速排序实现,从数组中选择一个key,数组中所有比key小的放左边,所有比key大的放右边,第一次递归,n个数被分为2部分,每部分2/n,第logn次递归,n个数被分为n部分,没部分为1,所以时间复杂度为nlogn
空间复杂度最坏情况n平方
如果第一次选择的是数组中的最大或最小值,则还需要递归n-1次,对于n个数来说需要n次递归,所以最坏时间复杂度为n的平方
#include3、归并排序
# include