《动手学深度学习 Pytorch版》 8.1 序列模型

到目前为止，我们遇到的数据主要是表格数据和图像数据，并且所有样本都是独立同分布的。然而，大多数的数据并非如此。比如语句中的单词、视频中的帧以及音频信号，都是有顺序的。

简言之，如果说卷积神经网络可以有效地处理空间信息，那么本章的循环神经网络（recurrent neural network，RNN）则可以更好地处理序列信息。循环神经网络通过引入状态变量存储过去的信息和当前的输入，从而可以确定当前的输出。

8.1.1 统计工具

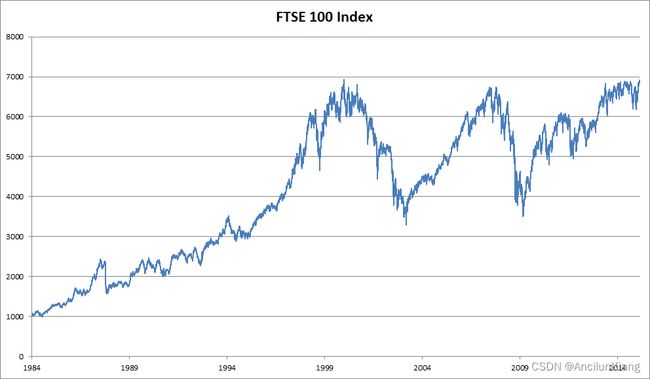
处理序列数据需要统计工具和新的深度神经网络架构。以下以富时100指数为例，用 $x_t$ 表示价格，即在时间步（time step） $t\in {\mathbb{Z}}^{+}$ 时，观察到的价格 $x$。需要注意的是，$t$ 对于本文中的序列通常是离散的，并在整数或其子集上变化。可以通过以下途径预测股市中表现良好的时间 $t$ 日：

$$x\sim P(x_t|x_{t-1},\dots ,x_1)$$

自回归模型

如果依然使用类似 3.3节的线性模型。最主要的问题就是输入数据的数量，输入数据的数量会随着我们遇到的数据量的增加而增加，因此需要一个近似方法来使这个计算变得容易处理。

评估 $P(x_t|x_{t-1},\dots ,x_1)$ 有以下两种策略：

• 自回归模型：

  序列 $x_{t-1},\dots ,x_1$ 可能不是必要的，可以取一个时间跨度 $\tau$，使用观测序列 $x_{t-1},\dots ,x_{t-\tau }$ 作为输入数据。自回归指的是对自己执行回归。

• 隐变量自回归模型：

  保留一些对过去观测的总结 $h_t$，并且同时更新预测 ${\hat{x}}_t$ 和总结 $h_t$。即使用 ${\hat{x}}_t=P(x_t|h_t)$ 估计 $x_t$，使用 $h_t=g(h_{t-1},x_{t-1})$ 更新模型。隐变量指的是 $h_t$ 从未被观察测到。

  

上述两个方法的整个序列的估计值都将通过以下的方式获得：

$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t|x_{t-1},\dots ,x_1)$$

马尔可夫模型

在自回归模型的近似法中使用时间跨度 $\tau$ 而不是全部序列来估计 $x_t$。只要这种是近似精确的，就可以说序列满足马尔可夫条件。

如果 $\tau =1$ 则得到一个一阶马尔可夫模型，$P(x)$ 由下式给出：

$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t|x_{t-1})当P(x_1|x_0)=P(x_1)$$

当 $x_t$ 仅是离散值时，使用动态规划可以沿着马尔可夫链精确地计算结果。如，我们可以高效地计算 $P(x_{t+1}|x_{t-1})$：

$$\begin{array}{rl}P(x_{t+1}|x_{t-1})& =\frac{{\sum }_{x_t}P(x_{t+1},x_t,x_{t-1})}{P(x_{t-1})}\\ & =\frac{{\sum }_{x_t}P(x_{t+1}|x_t,x_{t-1})P(x_t,x_{t-1})}{P(x_{t-1})}\\ & =\sum _{x_t}P(x_{t+1}|x_t)P(x_t|x_{t-1})\end{array}$$

因果关系

原则上，将 $P(x_1,\dots ,x_T)$ 倒序展开也没什么问题。事实上，基于一个马尔可夫模型还可以得到一个反向的条件概率分布。然而，在许多情况下，数据存在一个自然的方向，即在时间上是前进的。很明显，未来的事件不能影响过去。即如果我们改变 $x_t$ 可能会影响未来发生的事情 $x_{t+1}$，但不能反过来。也就是说，如果我们改变 $x_t$，基于过去事件得到的分布不会改变。因此，解释 $P(x_{t+1}|x_t)$ 比解释 $P(x_t|x_{t+1})$ 更容易。

8.1.2 训练

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

首先使用正弦函数和一些可加性噪声来生成序列数据，时间步为 $1,2,\dots ,1000$。

T = 1000  # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))  # 正弦函数叠加噪声
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

​

​

接下来将这个序列转换为模型的特征－标签对。

tau = 4  # 时间步长为4，即使用前四个状态预测第五个状态
features = torch.zeros((T - tau, tau))
for i in range(tau):  # features内容 0,1,2,3; 1,2,3,4; 4,5,6,7; ......
    features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))  # labels内容 4; 5; 6;......
# 最终效果4->0,1,2,3; 5->1,2,3,4; 6->4,5,6,7; ......

batch_size, n_train = 16, 600  # 只用前600个样本训练

train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                            batch_size, is_train=True)

在这里，我们使用一个相当简单的架构训练模型： 一个拥有两个全连接层的多层感知机，ReLU激活函数和平方损失。

# 初始化网络权重的函数
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)

# 一个简单的多层感知机
def get_net():
    net = nn.Sequential(nn.Linear(4, 10),
                        nn.ReLU(),
                        nn.Linear(10, 1))
    net.apply(init_weights)
    return net

# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

def train(net, train_iter, loss, epochs, lr):  # 常规训练流程
    trainer = torch.optim.Adam(net.parameters(), lr)
    for epoch in range(epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.sum().backward()
            trainer.step()
        print(f'epoch {epoch + 1}, '
              f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')

net = get_net()
train(net, train_iter, loss, 5, 0.01)

epoch 1, loss: 0.060140
epoch 2, loss: 0.056048
epoch 3, loss: 0.054582
epoch 4, loss: 0.050818
epoch 5, loss: 0.052746

8.1.3 预测

进行单步预测，用模型根据前面四个真实值预测后面一个值，效果不错，即使时间超过了 604 预测结果依然可信。

onestep_preds = net(features)  # 用模型根据前面四个真实值预测后面一个值
d2l.plot([time, time[tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
         'x', legend=['data', '1-step preds'], xlim=[1, 1000],
         figsize=(6, 3))

​

​

不使用真实值进行预测，而是使用前次预测的预测值进行预测。可以看到 604 以后的数据纯纯瞎搞。可能是由于预测误差一步步累积的结果。

multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
    multistep_preds[i] = net(  # 用前面四个预测值预测后一个
        multistep_preds[i - tau:i].reshape((1, -1)))

d2l.plot([time, time[tau:], time[n_train + tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy(),
          multistep_preds[n_train + tau:].detach().numpy()], 'time',
         'x', legend=['data', '1-step preds', 'multistep preds'],
         xlim=[1, 1000], figsize=(6, 3))

​

​

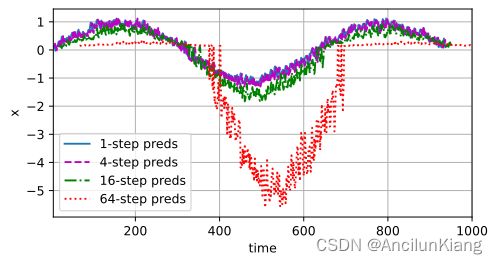
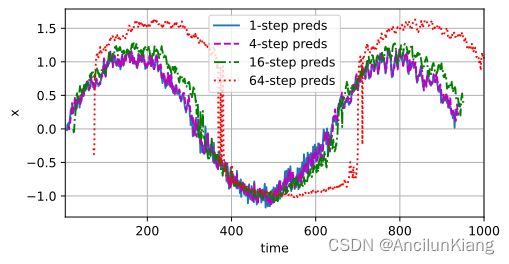
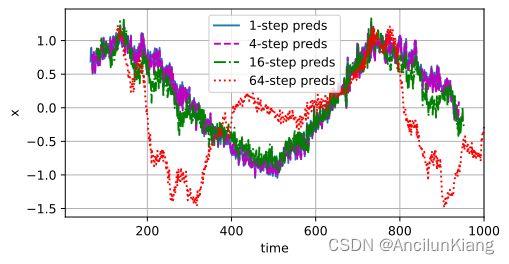
进行 k 步预测，即只给四个真实值，然后预测接下来 k 个点。下面分别用 k = 1, 4, 16, 64进行测试。可以看到1到16预测基本可信，虽然也是步长越大越不准。到64步时完全就是瞎预测了。

max_steps = 64

features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))

for i in range(tau):  # 填入前四个真实值
    features[:, i] = x[i: i + T - tau - max_steps + 1]

for i in range(tau, tau + max_steps):  # 进行最大步长的预测（小步长截取即可）
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)

steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
         [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
         legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
         figsize=(6, 3))

​

​

练习

（1）改进本节实验中的模型。

a. 是否包含了过去 4 个以上的观测结果？真实值需要是多少个？

b. 如果没有噪音，需要多少个过去的观测结果？提示：把 sin 和 cos 写成微分方程。

c. 可以在保持特征总数不变的情况下合并旧的观察结果吗？这能提高正确度吗？为什么？

d. 改变神经网络架构并评估其性能。

a. 这什么鬼翻译啊，明明就是让你试试不同的 tau，以下面的结果来看， tau稍大点有好处，但也不是越大越好

def test(tau):
    features = torch.zeros((T - tau, tau))
    for i in range(tau):
        features[:, i] = x[i: T - tau + i]
    labels = x[tau:].reshape((-1, 1))

    batch_size, n_train = 16, 600
    train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                                batch_size, is_train=True)

    def get_net():
        net = nn.Sequential(nn.Linear(tau, 10),
                            nn.ReLU(),
                            nn.Linear(10, 1))
        net.apply(init_weights)
        return net

    net = get_net()
    print(f'tau={tau}')
    train(net, train_iter, loss, 5, 0.01)

    max_steps = 64
    features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
    for i in range(tau):
        features[:, i] = x[i: i + T - tau - max_steps + 1]
    for i in range(tau, tau + max_steps):
        features[:, i] = net(features[:, i - tau:i]).reshape(-1)

    steps = (1, 4, 16, 64)
    d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
            [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
            legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
            figsize=(6, 3))

test(4)  # tau=4

tau=4
epoch 1, loss: 0.064608
epoch 2, loss: 0.054984
epoch 3, loss: 0.051668
epoch 4, loss: 0.051454
epoch 5, loss: 0.050462

test(8)  # tau=8

tau=8
epoch 1, loss: 0.070842
epoch 2, loss: 0.059001
epoch 3, loss: 0.052746
epoch 4, loss: 0.051375
epoch 5, loss: 0.045521

test(64)  # tau=64

tau=64
epoch 1, loss: 0.091182
epoch 2, loss: 0.105368
epoch 3, loss: 0.057070
epoch 4, loss: 0.052301
epoch 5, loss: 0.057420

test(16)  # tau=16

tau=16
epoch 1, loss: 0.062968
epoch 2, loss: 0.056878
epoch 3, loss: 0.047163
epoch 4, loss: 0.044272
epoch 5, loss: 0.047251

b. 没有噪音岂不是只要前一个就行了？

---

（2）一位投资者想要找到一种好的证券来购买。他查看过去的回报，以决定哪一种可能是表现良好的。这一策略可能会出什么问题呢？

证券需要考虑的特征可太多了，只看过去哪个回报高而不考虑复杂的影响因素所得的预测结果可能和抛硬币没啥区别。

---

（3）时间是向前推进的因果模型在多大程度上适用于文本呢？

文本的因果性应该更复杂些，比如某些文学性比较高的文章，倒叙、插叙、乱序之类的手法会很大的影响时间是向前推进的因果模型

---

（4）举例说明什么时候可能需要隐变量自回归模型来捕捉数据的动力学模型。

比如按分小组顺序汇报，每个组都会根据前一组的表现和老师点评来修正自己的PPT。