leetcode - 2251. Number of Flowers in Full Bloom

Description

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.

Example 1:

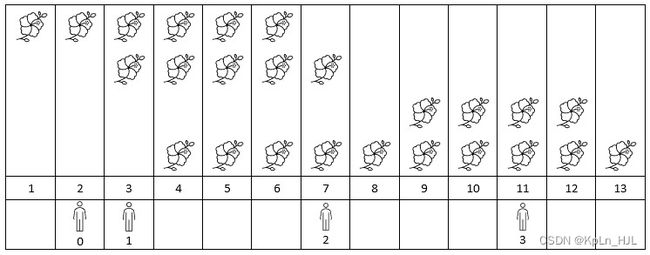
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], poeple = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

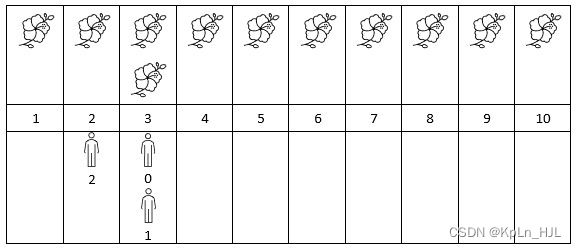
Input: flowers = [[1,10],[3,3]], poeple = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10^4
flowers[i].length == 2
1 <= starti <= endi <= 10^9
1 <= people.length <= 5 * 10^4
1 <= people[i] <= 10^9

Solution

Solved after hints…

Notice that for any given time t, the number of flowers blooming at time t is equal to the number of flowers that have started blooming minus the number of flowers that have already stopped blooming.

We can store the starting times in sorted order, which then allows us to binary search to find how many flowers have started blooming for a given time t. We do the same for the ending times to find how many flowers have stopped blooming at time t.

Time complexity: $o(n\ast \log n+n\ast \log n)=o(n\log n)$
Space complexity: $o(n)$

Code

class Solution:
    def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:
        start_flowers = [flowers[i][0] for i in range(len(flowers))]
        end_flowers = [flowers[i][1] for i in range(len(flowers))]
        start_flowers.sort()
        end_flowers.sort()
        res = []
        for each_people in people:
            start_index = bisect.bisect_right(start_flowers, each_people) + 1
            end_index = bisect.bisect_left(end_flowers, each_people) + 1
            res.append(start_index - end_index)
        return res

For using bisect package, remember:
bisect.bisect_left(a, x) returns i, so that a[:i] < x
bisect.bisect_right(a, x) returns i, so that a[:i] <= x