【无标题】AcWing算法基础课——基础算法
AcWing算法基础课
目录
1.1 快速排序
1.2 归并排序
1.3 二分算法
1.3.1 整数二分
1.3.2 实数二分
1.4 高精度加减乘除
1.4.1 高精度加法
1.4.2 高精度减法
1.4.3 高精度乘法
1.5 前缀和与差分
1.5.1 前缀和
1.5.2 差分
1.6 双指针
1.7 位运算
1.8 离散化
1.9 区间合并
1.1 快速排序
快速排序属于分治算法,快速排序的算法步骤,用分治的思想
- 确定分界点,数组内任意一个值(这里建议取中点,即(l+r)/2);
- 调整区间,让x左边的数都小于x,右边的数都大于x;
- 递归处理左右两个区间,直到细分到不能细分
对于第二步的调整区间,具体就是弄两个指针,分别指向数组的左右边界;不断的向中间遍历,将遍历过程中左边比x大的数和右边比x小的数交换;直到i,j相遇。
快排模版
void quick_sort(int q[],int l,int r)//放入数据:数组,左边界,右边界
{
if(l>=r) return ;//递归退出条件,不能在细分了
int i=l-1,j=r+1,x=q[l+r>>1];
while(ix);
if(i 1.2 归并排序
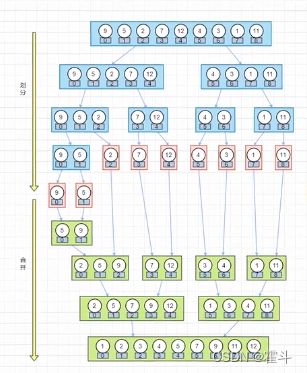
归并排序也属于分治算法;
- 确定分界点
- 递归成单个数
- 合并处理
具体思想:弄个临时数组,将已经排好序的两个部分通过两个指针将数从小到大放入临时数组,然后再将临时数组里面已经排好序的数放回本数组那段位置。
归并的流程图:
来源:B站up:请叫我AXin 讲的非常不错
归并模版
void merge_sort(int q[],int l,int r)
{
if(l>=r) return ;
int mid=l+r>>1,k=0;
merge_sort(q,l,mid); merge_sort(q,mid+1,r);
int i=l,j=mid+1;
while(i<=mid&&j<=r)//合并操作
{
if(q[i]<=q[j]) tmp[k++]=q[i++];
else tmp[k++]=q[j++];
}
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
for(i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];//转移操作,放回去
}1.3 二分算法
二分算是一个比较头疼的算法了,尤其是整数二分,如果边界问题没有处理好,就会要命了;
简单来说,二分就是找到你确定的那个分界点。
1.3.1 整数二分
步骤:
- 找到左右边界
- 找到中点(要么是(l+r>>1),要么是(l+r+1>>1))
当你写到 l=mid的时候,就需要把l+r变成l+r+1;
二分模版
int l=0,r=n-1;
while(l>1;
if(a[mid]>=k) r=mid;
else l=mid+1;
}
if(a[l]==k) cout<>1;
if(a[mid]<=k) l=mid;
else r=mid-1;
} 由于二分的特殊性,我决定拿一个题目来举例子;
第一题:题目链接
解题思想:
这个题目仔细一想,就是从一开始,每次把时间times加一,然后再把数组里面的每个小于times的数拿出来除个times再相加;
比如题目里面的例子: 当times为一的时候,把time数组里面的1拿出来,除个times,此时答案ans就等于一,小于5,所以需要继续加。
但是很明显这样暴力的枚举很难过,因为:
太大了。所以需要优化,怎么优化呢,可以发现,当时间times达到某一个值的时候,不论times怎么增加,后面的times都能使问题成立了,这就证明可以用二分来寻找答案。
思路:
- 找到times的上界和下界
- 寻找check函数,也就是判断当前点是大于交界点还是小于交界点
- 二分判断
答案:
class Solution {
public:
bool check(vector& time, int t, long long mid)
{
long long ans=0;
for(auto x : time)
{
if(ans>=t) return true;
ans+=mid/x;
}
return ans>=t;
}
long long minimumTime(vector& time, int t)
{
long long l=1;
long long r=1e16;
while(l> 1;
if(check(time,t,mid)) r=mid;
else l=mid+1;
}
return l;
}
}; 因为这个题目因为事r=mid,所以就不需要加+1了;
1.3.2 实数二分
一般的实数二分,条件是l与r都是相距的足够小;
下面是求某个数n(1e-4<=n<=1e4)的三次方根的二分代码:
#include
using namespace std;
int main()
{
double n; scanf("%lf",&n);
double l=-1e4,r=1e4;
while(r-l>1e-6)
{
double mid=(l+r)/2;
if(mid*mid*mid>n) r=mid;
else l=mid;
}
printf("%.6lf",l);
return 0;
} 一般当l与r的距离小于1e-6就差不多了。
1.4 高精度加减乘除
这个是指将特别大的整数存在字符串和数组里面进行处理,因为进位的原因,所以一般是倒着存,将高位存在后面,低位存在前面,也就是把个位存在首位,把十百千依次往后存。
1.4.1 高精度加法
这个算的是两个大整数的加法,方法与小学学过的加法思想一样,上过小学的应该都知道。
- 先将两个大整数存于字符串之中
- 将其反过来放在两个数组之中
- 按照小学加法进行运算
代码模版:
vector add(vector &A,vector &B)
{
vector C;
int t=0;
for(int i=0;i 解释: 从个位开始遍历A和B,用t来存储这一位相加的结果,t%10,就是这一位的结果,将t/10,就是处理了下一位的进位;最后,如果t不为0,就证明还有一个进位,将其加上即可。
注意: 如果不用&的话,A,B数组,使用add函数的时候会将A,B‘函数拷贝一遍,而使用引用&,就减少了拷贝所需要的时间。
数组A,B的处理:
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
auto C=add(A,B);
for(int i=C.size()-1;i>=0;i--) cout<输入字符串后,倒叙存在A,B中,最后C中的也是倒着的,倒着输出就行。
1.4.2 高精度减法
因为减法可能存在小数减大数的情况,所以需要处理一下
- 倒着存入A,B;
- 判断两个数谁大,A大就直接A“-”B,否则先输出一个“-”,,在输出B”-“A;
- 小学减法
由于需要判断两个数哪个大,所以需要一个cmp函数来判断
bool cmp(vector &A,vector &B)
{
if(A.size()!=B.size()) return A.size()>B.size();
for(int i=A.size()-1;i>=0;i--)
{
if(A[i]!=B[i]) return A[i]>B[i];
}
return true;
}//为什么不能用strcmp来比较,因为这个函数是从头开始比较字典序的,
//比如12345和678这两个数,就会判断错误
代码模版:
vector sub(vector &A,vector &B)
{
vector C;
int t=0;
for(int i=0;i1&&!C.back()) C.pop_back();//因为我们是前面存的低位,后面存的高位,所以需要将后面的0都去掉,保证没有前导0
return C;
} 主函数部分:
int main()
{
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
vector C;
if(cmp(A,B))
{
C=sub(A,B);
}
else
{
cout<<'-';
C=sub(B,A);
}
for(int i=C.size()-1;i>=0;i--) cout< 有了加减法之后,像加一个负数或者减一个负数什么的,就可以替换成减法或者加法来做。
1.4.3 高精度乘法
1.5 前缀和与差分
1.5.1 前缀和
前缀和就是某一个数组中,前多少个数的和,我们一般定义一个sum数组存a数组的前缀和,下标为i代表着a数组中前i个数的和。
前缀和一般是用来解决多次查询某一个数组的某个区间的和是多少,能用o(1)的时间复杂度解决。
代码模版:
#include
using namespace std;
const int N=1e5+10;
int a[N],sum[N];
int main()
{
int n,m; scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) //前缀和处理
{
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++) sum[i]+=sum[i-1]+a[i];
int l,r;
while(m--)//查询操作
{
scanf("%d%d",&l,&r);
printf("%d\n",sum[r]-sum[l-1]);
}
return 0;
} 前缀和处理还可以简写成这样:
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
a[i]+=a[i-1];
}直接用原数组存,如果原数组在问题中不再需要的时候
注意:for循环从一开始,是因为,有i-1这个操作。
说完一维的前缀和数组,接下来就是进阶版的二维前缀和数组
在一个矩阵中,给你两个点的坐标,分别是矩阵的左上角坐标和右下角坐标,让你求两个坐标围成的子矩阵中所有数的和;
关于前缀和数组的处理有图分析:题解链接
- 首先是前缀和数组的处理
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
}
}
每一个坐标[i][j],代表的就是以[0][0],[i][j]为左上角坐标和右下角坐标的子矩阵的和。
求子矩阵:
int x1,x2,y1,y2;
while(q--)
{
cin>>x1>>y1>>x2>>y2;
cout<1.5.2 差分
差分就是什么呢,比如说a数组是b数组的前缀和数组,那么b数组就是a数组的差分数组。
差分可以干什么呢,它可以在o(1)的时间复杂度下将a数组中的[l,r]区间上的每一个数都加上x;
差分模版:
#include
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main()
{
int n,m; scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[i]=a[i]-a[i-1];
int l,r,c;
while(m--)
{
scanf("%d%d%d",&l,&r,&c);
b[l]+=c,b[r+1]-=c;
}
for(int i=1;i<=n;i++) b[i]+=b[i-1],printf("%d ",b[i]);
return 0;
} 差分数组的实现还有一种方法:
void insert(int b[],int l,int r,int c)
{
b[l]+=c;
b[r+1]-=c;
}
定义一个差分的函数,然后 for(int i=1;i<=n;i++) scanf("%d",&a[i]),insert(b,i,i,a[i]);就可以了。
有图分析:题解链接
二维差分,也就是差分矩阵。就是一维差分的升级版,将子矩阵的每一个元素都加上x;
模版:
#include
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1]+=c;
b[x1][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c;
}
int main()
{
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
insert(i,j,i,j,a[i][j]);
}
}
int x1,y1,x2,y2,c;
while(q--)
{
cin>>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
b[i][j]+=b[i][j-1]+b[i-1][j]-b[i-1][j-1];
cout< 1.6 双指针
双指针一般是用来降低时间复杂度的算法;指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同方向( 快慢指针 )或者相反方向( 对撞指针 )的指针进行扫描,从而达到相应的目的。
题目链接
解答:
#include
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main()
{
int n; cin>>n;
for(int i=0;i>a[i];
}
int ans=0;
for(int i=0,j=0;i1)
{
b[a[j]]--;
j++;
}
ans=max(ans,i-j+1);
}
cout< 本题使用了哈希的思想加上双指针的算法,下面是大佬的部分题解:
双指针的使用很灵活,各种想不到的方法都可以用,而且一般是与其他的思想结合在一起使用,需要多找点题目来联系。
1.7 位运算
位运算是用符号如:^,&,|,<<,>>等符号进行数的处理,因为它是直接在二进制的基础上进行处理,所以一般比加减乘除快很多,并且还能用它去完成很多操作;接下来演示一下;
- 判断二进制中一的个数:
int lowbit(int x)
{
return x&-x;
}这个函数可以截取某个二进制数的最后面一个1及后面的所有的0;
比如 10101000 , 这个数的负数形式在计算机里面就是它的补码,也就是反码加一,为:01011000,这个时候,二者按位与得到了1000,也即是最后面一个1及后面的所有的0;
利用这个函数,每次都减去这个1,直到这个数为0,就可以得到所有一的个数了;
代码:
#include
using namespace std;
int main()
{
int n; scanf("%d",&n);
int x,ans;
while(n--)
{
ans=0;
scanf("%d",&x);
while(x) x-=x&-x,ans++;
printf("%d ",ans);
}
return 0;
} (更多位运算......)
1.8 离散化
离散化:定义取自这篇博客
离散化就是将无限空间中的值映射到有限的空间内,去提高算法的时空复杂度。
什么时候会用到离散化呢? 当一个非常大的数组需要开,但是操作的数特别少,就可一使用离散化,将间隔很大的点,映射到相邻的数组元素中,增加空间的利用。
比如下面这道题:题目链接
- 将操作的数的下标存到一个数组alls中去,再将操作的数值和对应的下标存到一个数组add里面去
- 将需要查询的下标也存到alls里面去
- 排序,去重
- 查询
在这里,需要一个函数find去查询元原下标在新数组alls里面对应的下标是什么
代码:
#include
#include
#include
using namespace std;
const int N=3e5+10;
typedef pair PII;
int a[N];
vectoralls;//allls数组用来存原数组下标
vectoradd,query;//add用来存初始化的n次操作中的x,c;
//query数组存的是查询的边界l,r;
int find(int x)//用来寻找原来的x在现在的新数组里面下标是什么
{
int l=0,r=alls.size()-1;
while(l>1;
if(alls[mid]>=x) r=mid;
else l=mid+1;
}
return r+1;//因为要求前缀和,所以需要加1,方便
}
int main()
{
int n,m;
cin>>n>>m;
int x,k;
for(int i=1;i<=n;i++)
{
cin>>x>>k;
alls.push_back(x);
add.push_back({x,k});
}
int l,r;
for(int i=1;i<=m;i++)
{
cin>>l>>r;
query.push_back({l,r});
alls.push_back(l);
alls.push_back(r);//之所以也要存l,r,是因为后面要查询映射值的时候好查
}
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());//排序去重操作
for(int i=0;i 1.9 区间合并
题目链接