神的规范：排序算法（五）：归并排序

写在前面：
排序又称为分类，它是数据处理中经常用到的一种重要运算。
虽然并未列入世界最伟大的几大算法之一，但毫无疑问，在各行各业的各个时期排序都是作为奠基者般的存在为程序所调用，也为编程者所敬仰。只是，也许正是因为它与我们息息相关，以至于我们竟然时常忽略它的存在。
事实上我们生活中无时无刻不在做排序：考试成绩排名，按身高、年龄、能力高低去评判他人，划分任务处理的优先级，等等·······
前面4篇博客我们讨论了简单插入排序、简单选择排序、冒泡排序和本领卓越的快速排序，而今天我们进入排序的最后一讲“归并排序”的学习，一步步去探索排序算法如何在反思中前进，在山重水复处柳暗花明。

其实，归并排序的思路可以看做是快速排序的逆向思考：
我们已经知道，所谓快排，采用的是一种分治策略，将一个大的待排序列逐步分化成小的序列，各个击破。当每个序列都只有一个元素是，整个序列的排序也就完成了。
而归并排序恰好反其道而行之，先把待排序列的每一个元素都看成是一个小序列，然后层层两两合并成有序序列，直到最终序列包含了原始待排序列的所有元素，整个序列元素已然有序。由归并排序的基本思想可以看出，最关键的一步是如何把两个位置相邻的有序子序列合并成一个有序序列。
下面我们来讨论归并排序的的基本算法：
设两个有序序列存储在一维数组a中，有序子序列1是从a[1]到a[m]，有序子序列2是从a[m+1]到a[r]。将归并后的有序序列放在一个一维数组x中，则x是从x[1]到x[r]。
（1）设置三个变量i，j，k，其中i，j分别代表序列1和2中要比较大小的相应元素，初始值应分别为1和m+1；k代表数组x的位置号，应从1开始。
（2）反复比较a[i]与a[j]的大小，将小数存储在x[k]中并将相应的小数下标和x元素下标加一。
（3）当序列1或2中的全部元素都已放置在数组x[k]中，即i = m或者j = r时，比较结束，然后将另一序列中所有剩余元素搬至数组x中，如此一来就完成了有序序列1和2的合并。

下面我们来给出一次归并排序的算法的C语言表示（假设待排元素为double型数据）：

void mergesort(double a[],int n) {
    int i,len;
    double x[NUM];     //New array to store elements
    len = 1; 
    while (len < n) {  //len changes every time
        merge(a,x,len,n); 
        for (i = 0;i < n;i++)  //Transfer elements back to aboriginal array
            a[i] = x[i];
        len = 2*len;   
    }
}

void merge(double a[],double x[],int len,int n) {  //a=primary array,x=new array which as output,len=step every time,n is array border
    int i,j,k = 0;
    int l1,l2,r1,r2;   //means left border and right border for sequence 1 and 2 respectively
    l1 = 0;

    while (l1 + len < n-1 ) {  //Loop until left border is at an end
        r1 = l1 + len -1;
        l2 = r1 + 1;
        r2 = (l2 + len -1 <= n-1) ? l2+ len -1 : n-1;
        for (i = l1,j = l2;i <= r1 && j <= r2;k++) {   //x[k] changes one by one
            if (a[i] <= a[j]) {
                x[k] = a[i];
                i++;
            }
            else {
                x[k] = a[j];
                j++;
            }
        }
        while (i <= r1) { //If sequence 1 is not ended
            x[k] = a[i];
            i++;
            k++;
        }
        while (j <= r2) { //If sequence 2 is not ended
            x[k] = a[j];
            j++;
            k++;
        }
        l1 = r2 + 1;   //Execute by step
    }

    for (i = l1; i < n;i++,k++)  //If there are not enough elements in primary sequence to make up a group
        x[k] = a[i];
}   

可以看到，归并排序的代码还是比较复杂的，需要考虑的因素也比较多，实际上使用率也不是很高。
下面证明一下它的排序功能可以实现：

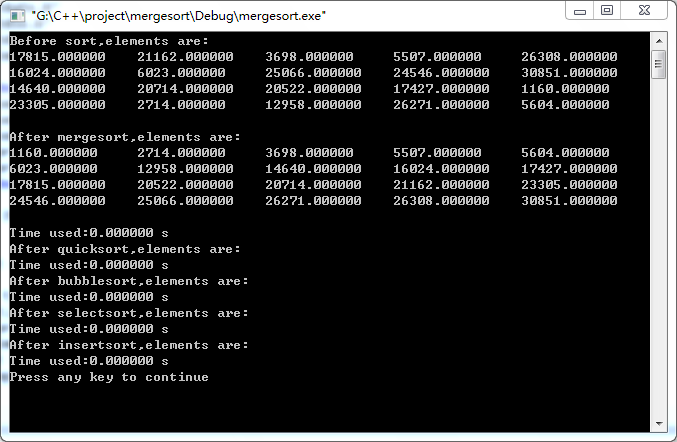
接下来，要证明我们前面的一个论断：归并排序也是排序界的一大高手，何出此言呢？先来几张图证明一下它的实力，再来说明为何如此：
5000个数据时：

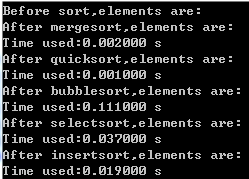
10000个数据时：

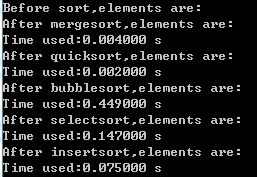
20000个数据时：

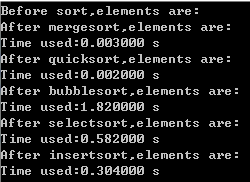
可以看到，归并排序速度略慢于快排（快排不愧是排序界的独孤求败），但是仍远远超过插入、选择和冒泡排序。
其实在算法复杂度上也很好理解，它同样是O[nlogn]，与快排相当。但是它不足的一点就是，在计算中需要一个和原始数组相同大小的辅助数组（代码中用x[]表示），占用了更多的存储空间。而且它在移动数据的开销上也大于快排。

那么，我们在五篇博客里也讨论了五种排序的算法，并且比较了它们的性能，相信大家对它们也都有了足够的了解。
至此，排序算法的博客就告一段落啦~虽然还有哈希排序、堆排序、基数排序等等经典算法未涉及，但是相信在以后的内容中多少也能捕捉到它们的影子，至于哈希，我将会在新的博客内容（神的目光：查找算法）里做一个系列分享。

Goodbye!