算法训练Day42 | 01背包问题的理论基础(二维和一维dp数组的全面剖析);LeetCode416. 分割等和子集(01背包的应用)
目录
01背包问题的理论基础
方法一:二维dp数组01背包
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
方法二:一维dp数组01背包(滚动数组)
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode416. 分割等和子集
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
01背包问题的理论基础
背包问题系列:
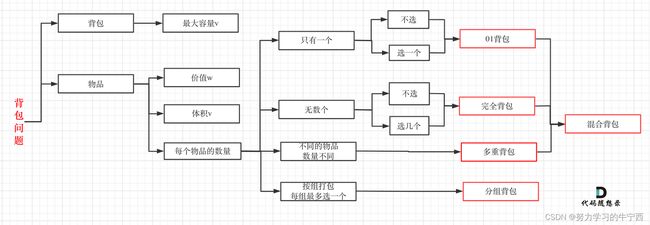
对于面试的话,其实掌握01背包,和完全背包,就够用了,最多可以再来一个多重背包;至于其他背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了;
而完全背包又是也是01背包稍作变化而来,即:完全背包的物品数量是无限的,**所以背包问题的理论基础重中之重是01背包,一定要理解透!**leetcode上没有纯01背包的问题,都是01背包应用方面的题目,也就是需要转化为01背包问题。所以我先通过纯01背包问题,把01背包原理讲清楚,后续再讲解leetcode题目的时候,重点就是讲解如何转化为01背包问题了。
题目描述
(LeetCode上没有纯粹的01背包问题)
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
方法一:二维dp数组01背包
1. 思路
这是标准的背包问题,以至于很多同学看了这个自然就会想到背包,甚至都不知道暴力的解法应该怎么解了。这样其实是没有从底向上去思考,而是习惯性想到了背包;
那么暴力的解法应该是怎么样的呢?
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是o(2^n),这里的n表示物品数量。所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
讲解所用到的例子:
背包最大重量为4,物品如下:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?以下讲解和图示中出现的数字都是以这个例子为例。
动态规划五部曲
1.1 确定dp数组以及下标的含义
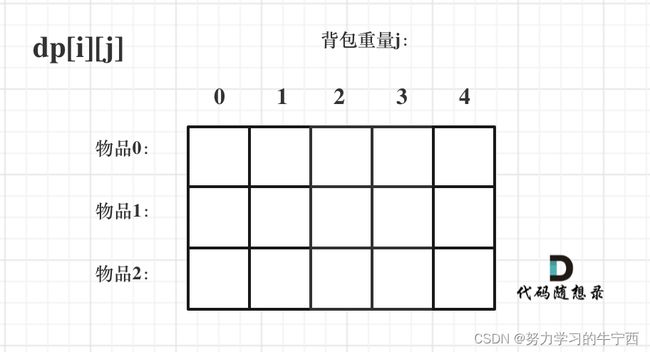
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
只看这个二维数组的定义,大家一定会有点懵,看下面这个图:
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的 ,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
1.2 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少,那么可以有两个方向推出来dp[i][j]:
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值;
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
1.3 dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱,首先回顾一下递推公式,看看到底要初始化那些元素?
递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
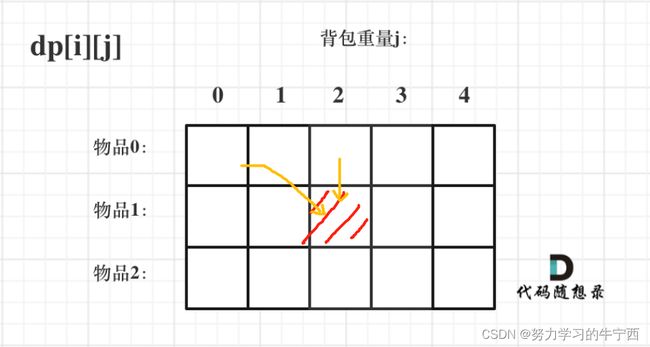
如果要得到dp[i][j],就要知道dp[i - 1][j]和dp[i - 1][j - weight[i]] ;dp[i - 1][j]在dp[i][j]的正上方,dp[i - 1][j - weight[i]]在dp[i][j]的左上方;
看清楚位置之后,我们就知道了,需要初始化的是这个矩阵的第一行以及第一列:
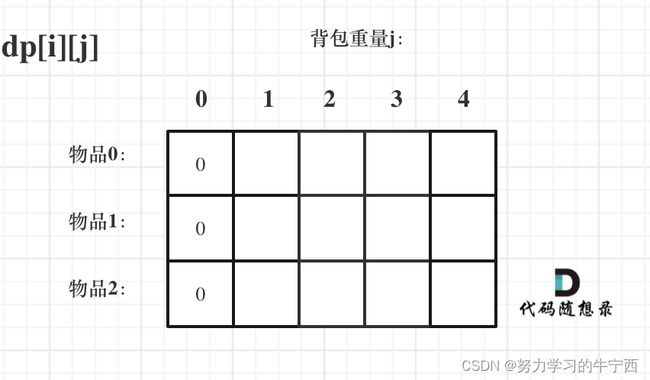
首先看第一列
如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
再看第一行
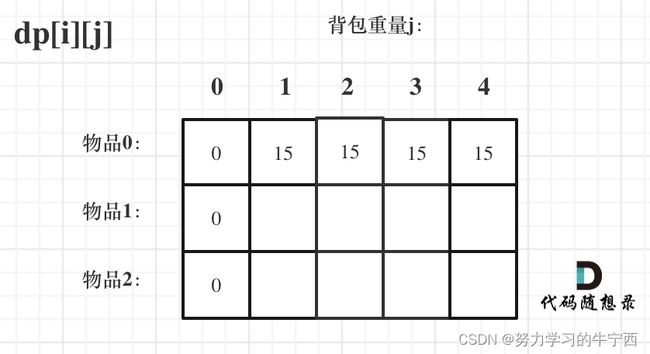
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值;
- 那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小;
- 当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
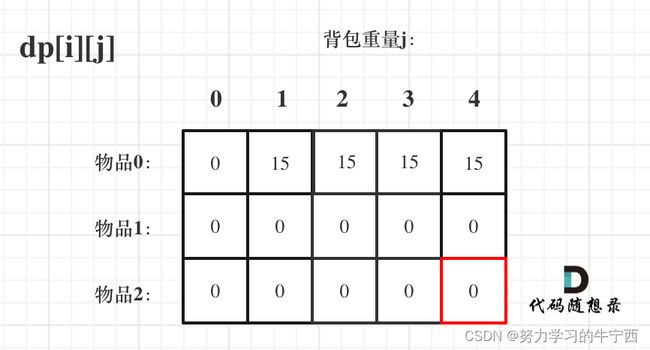
其他位置怎么初始化?
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。初始-1,初始-2,初始100,都可以!
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
最后初始化部分的代码如下:
def test_2_wei_bag_problem1(bag_size, weight, value) -> int:
rows, cols = len(weight), bag_size + 1
dp = [[0 for _ in range(cols)] for _ in range(rows)]
# 初始化dp数组.
for i in range(rows):
dp[i][0] = 0
first_item_weight, first_item_value = weight[0], value[0]
for j in range(1, cols):
if first_item_weight <= j:
dp[0][j] = first_item_value平时初始化dp数组很多时候是凭感觉来的,但有时候感觉是不靠谱的!
一个要注意的点
如果物品0的重量是2的话,那么i=0,j=1的位置应该初始化为0;
1.4 确定遍历顺序
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以,为什么也是可以的呢?要理解递归的本质和递推的方向。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的;
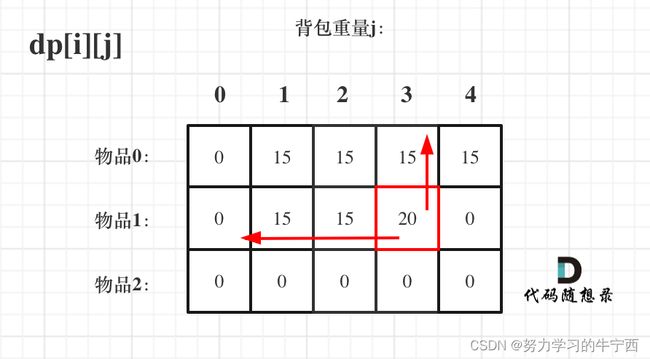
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
一行一行,由左到右,由上到下,这样的顺序可以保证遍历到每个位置的时候,它的正上方和左上方都是有值的;所以先物品再背包的顺序OK;
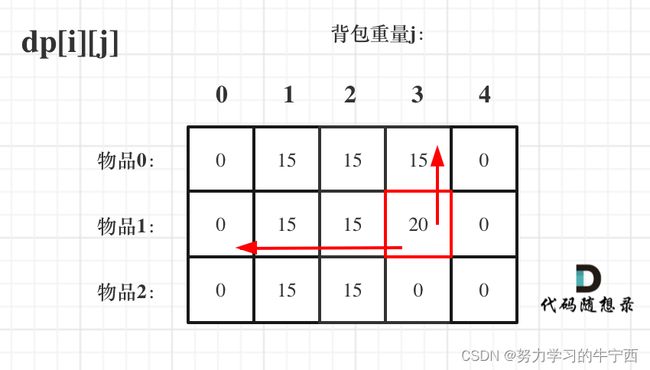
再来看看先遍历背包,再遍历物品呢,如图:
一列一列,从上到下,从左到右,这样的顺序也可以保证遍历到每个位置的时候,它的正上方和左上方都是有值的;所以先背包再物品的顺序也OK;
Conclusion:
大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!但先遍历物品再遍历背包这个顺序更好理解;
所以本质上就是看:得到dp[i][j],需要哪里的数,然后某种遍历顺序是否能够先产生那些位置的数,就可以了;本题中就是只要保证dp[i][j]的上方和左上方有值即可,其实背包问题里,两个for循环的先后循序是非常有讲究的,理解遍历顺序其实比理解推导公式难多了。
1.5 举例推导dp数组
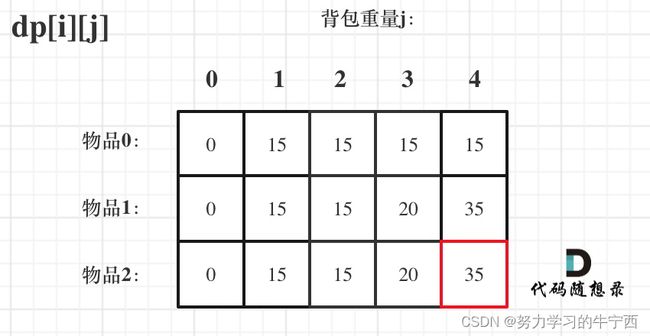
来看一下对应的dp数组的数值,如图:
在自己举例的过程中,发现不可以直接就在两个for loop下面写递推公式, dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);因为j - weight[i]的值是可能小于0 的,说明当前的背包容量不能装下物品i,所以就只有不装物品i 的那种可能性了;
最终结果就是dp[2][4]。建议大家此时自己在纸上推导一遍,看看dp数组里每一个数值是不是这样的,做动态规划的题目,最好的过程就是自己在纸上举一个例子把对应的dp数组的数值推导一下,然后在动手写代码!
很多同学做dp题目,遇到各种问题,然后凭感觉东改改西改改,怎么改都不对,或者稀里糊涂就改过了;主要就是自己没有动手推导一下dp数组的演变过程,如果推导明白了,代码写出来就算有问题,只要把dp数组打印出来,对比一下和自己推导的有什么差异,很快就可以发现问题了。
2. 代码实现
def bag_problem01_2d(bagsize,weight,value):
row = len(weight)
col = bagsize+1
# 初始化dp数组
dp = [[0 for _ in range(col)] for _ in range(row)]
print(dp)
for j in range(col):
if j >= weight[0]:
dp[0][j] = value[0]
# # 更新dp数组: 先遍历物品, 再遍历背包.
for i in range(1,row):
curWeight = weight[i]
curValue = value[i]
for j in range(1,col):
# 说明背包装不下当前物品
if j < curWeight:
# 所以不装当前物品.
dp[i][j] = dp[i-1][j]
else:
# 定义dp数组: dp[i][j] 前i个物品里,
# 放进容量为j的背包,价值总和最大是多少;
dp[i][j] = max(dp[i-1][j],dp[i-1][j-curWeight]+curValue)
print(dp)
return dp[row-1][col-1]
print(bag_problem01_2d(4,[1,3,4],[15,20,30]))
3. 复杂度分析
-
时间复杂度:O(m*n)
m为背包容量,n为物品个数;DP数组的每个位置都需要遍历求一遍,每次遍历的时候需要做的计算是常数级别,DP数组的位置个数为m*n;
-
空间复杂度:O(m*n)
m为背包容量,n为物品个数;dp数组所需的储存空间是m*n;
4. 思考与收获
- 讲了这么多才刚刚把二维dp的01背包讲完,**其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在如何初始化和遍历顺序上;**可能之前并没有注意到初始化 和 遍历顺序的重要性,我们后面做力扣上背包面试题目的时候,就会感受出来了;
方法二:一维dp数组01背包(滚动数组)
1. 思路
对于背包问题其实状态都是可以压缩的,其实并不用一个二维数组来记录,用一个一维数组就够了,下面讲解思路;
还是用这个例子讲解:背包最大重量为4,物品信息如下:
问背包能背的物品最大价值是多少?
在使用二维数组的时候:递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组);这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了,i是物品,j是背包容量。dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。一定要时刻记住这里i和j的含义,要不然很容易看懵了。
动态规划五部曲
1.1 确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j];
1.2 一维dp数组的递推公式
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
其实逻辑还是和二维数组中一样的,dp[j]有两种选择,要么放物品i,要么不放物品i;
- 如果不放物品i;取自己dp[j] 即可,相当于 二维dp数组中的dp[i-1][j];
- 如果放物品i;dp[j - weight[i]] + value[i];dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
所以递推公式是:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
对比二维的递推公式:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]+value[i])
可以看出相对于二维dp数组的写法,就是把dp[i][j]中i的维度去掉了。
1.3 一维dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp[j] 是由本身和前面的值加上一个value取最大值推导而来,那么本身应该初始化一个非负数的最小值,才不会因为初始化了一个很大的值,覆盖了在递推公式中本来应该计算的值,那么非0下标都初始化为0就可以了。这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了;
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
1.4 一维dp数组遍历顺序
# 先遍历物品, 再遍历背包容量
for i in range(len(weight)):
for j in range(bag_weight, weight[i] - 1, -1):
# 递归公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
why倒序?二维dp遍历的时候,背包容量是从小到大,而为什么一维dp遍历的时候,背包是从大到小?
最容易理解的解释是:
- 倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖;
- 二维数组情况下,用i-1行的已知最大价值来推断,换句话说是左上角的数据
- 但是换成一维数组的话,左上角的数据就是数组左边的数据,因此,只能从右边开始遍历背包的容量;
- 如果从左边开始遍历的话,相当于左边的数已经不是原来的i-1行的数据了,是已经被更新了的数据,这个数据就会导致物品i可能会被放入多次,导致结果错误;
总结来说,倒序遍历是为了保证物品i只被放入一次!倒序才能拿到原来左侧的旧值,而不是被更新过的。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
Example:
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
那么问题又来了,为什么二维dp数组历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!两层的数据是完全独立的,不会相互影响;
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品(Carl的理解方法,但是这个说法我不是很理解)
我认为首先倒着来的话,dp数组根本都不能压缩成一维的,因为这样的话是一列一列的遍历,我们当前列还没开始修改的时候,只有上一列的数值;
根据二维递推的公式:dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]+value[i])
dp[i-1][j]这个相当于是每列每列的前一个数值,但这个dp[i-1][j-weight[i],就不固定到底是前面那一列的数值了,所以说我认为这种遍历方式直接都不能压缩成一维的滚动数组;
1.5 举例推导dp数组
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
2. 代码实现
def bag_problem01_1d(bagsize,weight,value):
# 初始化: 全为0
dp = [0]*(bagsize+1)
# 先遍历物品, 再遍历背包容量
for i in range(len(weight)):
# 逆序遍历背包容量,截止的地方是j-weight[i]=0的地方
for j in range(bagsize,weight[i]-1,-1):
# 递推公式
dp[j] = max(dp[j],dp[j-weight[i]]+value[i])
print(dp)
return dp[-1]
print(bag_problem01_1d(4,[1,3,4],[15,20,30]))
3. 复杂度分析
-
时间复杂度:O(m*n)
m为背包容量,n为物品个数;需要用每个物品i 都遍历一遍背包,所以要遍历m*n次数;
-
空间复杂度:O(m)
m为背包容量,n为物品个数;dp数组所需的储存空间长度为背包容量+1;
4. 思考与收获
-
可以看出,一维dp 的01背包,要比二维简洁的多! 初始化 和 遍历顺序相对简单了;所以我倾向于使用一维dp数组的写法,比较直观简洁,而且空间复杂度还降了一个数量级!在后面背包问题的讲解中,我都直接使用一维dp数组来进行推导;
-
以上的讲解可以开发一道面试题目(毕竟力扣上没原题)。
就是本文中的题目,要求先实现一个纯二维的01背包,如果写出来了,然后再问为什么两个for循环的嵌套顺序这么写?反过来写行不行?再讲一讲初始化的逻辑。
然后要求实现一个一维数组的01背包,最后再问,一维数组的01背包,两个for循环的顺序反过来写行不行?为什么?
注意以上问题都是在候选人把代码写出来的情况下才问的。就是纯01背包的题目,都不用考01背包应用类的题目就可以看出候选人对算法的理解程度了。相信大家读完这篇文章,应该对以上问题都有了答案!
-
此时01背包理论基础就讲完了,把01背包的dp数组定义、递推公式、初始化、遍历顺序从二维数组到一维数组统统深度剖析了一遍,没有放过任何难点;都理解了之后,后面我们在做01背包的题目,就会发现非常简单了;不用再凭感觉或者记忆去写背包,而是有自己的思考,了解其本质,代码的方方面面都在自己的掌控之中。即使代码没有通过,也会有自己的逻辑去debug,这样就思维清晰了。
Reference:
- 代码随想录 (programmercarl.com)
- 代码随想录 (programmercarl.com)
本题学习时间:180分钟。
LeetCode416. 分割等和子集
LeetCode416. 链接:416. 分割等和子集 - 力扣(LeetCode)
1. 思路
这道题目是要找是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。那么只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。本题是可以用回溯暴力搜索出所有答案的,但最后超时了,也不想再优化了,放弃回溯,直接上01背包吧。
背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。要注意题目描述中商品是不是可以重复放入。即一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。那么来一一对应一下本题,看看背包问题如果来解决。
只有确定了如下四点,才能把01背包问题套到本题上来:
- 背包的容量: 为sum;
- 商品的重量and价值:重量和价值都为元素的数值;
- 背包如果正好装满,说明找到了总和为sum/2 的子集;
- 背包中每一个元素是不可重复放入的。
以上分析完,我们就可以套用01背包,来解决这个问题了。
动态规划五部曲
1.1 确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值可以最大为dp[j]。
套到本题,dp[j]表示 背包总容量是j,最大可以凑成j的子集总和为dp[j];
1.2 确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
1.3 dp数组如何初始化
在01背包,一维dp如何初始化,已经讲过;
从dp[j]的定义来看,首先dp[0]一定是0。如果如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
dp数组长度应该是多少?
- dp[i]中的i表示背包内总和,题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200,总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了;
- 也可以直接初始化为长度为target+1的全是0 的数组;
1.4 确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
1.5 举例推导dp数组
dp[j]的数值一定是小于等于j的。如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
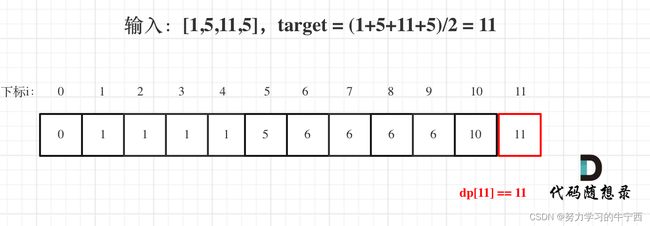
用例1,输入[1,5,11,5] 为例,如图:
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等;
2. 代码实现
# time:O(N*target);space:O(target)
class Solution(object):
def canPartition(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
# dp[j]的定义
# 背包容量为j,其中可以装的物品的最大总和为dp[j]
# 物品的重量为 nums数组,价值也为nums数组
# target = sum(nums)/2 如果dp[target] = target: return True
# 边界情况处理,如果是奇数,不可能平分
total = sum(nums)
if total %2 == 1: return False
target = total//2
# 初始化
dp = [0]*(target+1)
# 遍历顺序,外物品,内逆序背包容量
for i in range(len(nums)):
for j in range(target,nums[i]-1,-1):
# 递推公式
dp[j] = max(dp[j],dp[j-nums[i]]+nums[i])
# 背包容量为target的时候,其中可以装的物品的最大总和为dp[target]
return dp[target] == target
3. 复杂度分析
-
时间复杂度:O(n*target)
其中n为数组的长度(物品个数),target是整个数组的元素和的一半;需要计算出所有的状态,每个状态计算的时间复杂度为O(1);
-
空间复杂度:O(target)
其中 target是整个数组的元素和的一半;空间复杂度取决于dp数组,数组长度就是target+1;
4. 思考与收获
- 这道题目就是一道01背包应用类的题目,需要我们拆解题目,然后套入01背包的场景;(难点)01背包相对于本题,主要要理解,题目中物品是nums[i],重量是nums[i],价值也是nums[i],背包体积是sum/2;看代码的话,就可以发现,基本就是按照01背包的写法来的;
- (二刷再看)这道题目初步看,是如下两题几乎是一样的,可以用回溯法,解决如下两题
- 698.划分为k个相等的子集
- 473.火柴拼正方形
Reference:代码随想录 (programmercarl.com)
本题学习时间:60分钟。
本篇学习时间为4小时,总结字数10000+,把最基础的01背包问题的一维和二维做法非常全面的做了剖析,并且做了一道01背包的运用的题目,在我看来最难的过程是理解并套用到01背包问题的这个过程。(求推荐!)