【verilog学习23】HDLBits:Circuits_Sequential Logic_Finite State Machines
【HDLBits】Circuits_Sequential Logic_Finite State Machines
- I FSM 1 (asynchronous reset) (Fsm1)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- II FSM 1 (synchronous reset) (Fsm1s)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- III FSM 2 (asynchronous reset) (Fsm2)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- IV FSM 2 (synchronous reset) (sm2s)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- V Simple State transitions 3 (Fsm3comb)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- VI Simple one-hot State transitions 3 (Fsm3onehot)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- VII Simple FSM 3 (asynchronous reset) (fsm3)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- VIII Simple FSM 3 (synchronous reset) (Fsm3s)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- IX Design a moore FSM(Exams/ece241 2013 q4)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- X Lemmings 1
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XI Lemmings2
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XII Lemmings3
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XIII Lemmings4
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XIV One-hot FSM
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XV PS/2 packet parser
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XVI PS/2 packet parser and datapass
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XVII Serial receiver (Fsm serial)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XVIII Serial receiver and datapath
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- XIX Serial receiver with parity checking
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 20 Sequence recognition
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 21 Q8: design a Mealy FSM
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 22 Q5a: Serial two's complementer(Moore FSM)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 23 Q5b: Serial two's complementer(Mealy FSM)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 24 Q3a FSM(Exams/2014 q3fsm)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 25 Q3b:FSM(Exams/2014 q3bfsm)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 26 Q3c:FSM logic
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 27 Q6b:FSM next state logic
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 28 Q6c:FSM one-hot next state logic
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 29 Q6:FSM (Exams/m2014 q6)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 30 Q2a:FSM (Exams/2012 q2fsm)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 31 One-hot FSM equations (Exams/2012 q2b)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 32 Q2a:FSM (Exams/2013 q2afsm)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
- 33 Q2b:Another FSM (Exams/2013 q2bfsm)
-
- 1.代码编写
- 2.提交结果
- 3.题目分析
状态机简单介绍 {\color{plum}\small\textbf{状态机简单介绍}} 状态机简单介绍
https://blog.csdn.net/qq_39507748/article/details/108763514
I FSM 1 (asynchronous reset) (Fsm1)
1.代码编写
module top_module(
input clk,
input areset, // Asynchronous reset to state B
input in,
output out);//
parameter A=0, B=1;
reg state, next_state;
always @(*) begin // This is a combinational always block
// State transition logic
case(state)
A: begin
if(in==1'b1) begin
// out = 1'b0;
next_state = A;
end
else begin
// out = 1'b0;
next_state = B;
end
end
B: begin
if(in==1'b1) begin
// out = 1'b1;
next_state = B;
end
else begin
// out = 1'b1;
next_state = A;
end
end
endcase
end
always @(posedge clk, posedge areset) begin // This is a sequential always block
// State flip-flops with asynchronous reset
if(areset)
state <= B;
else
state <= next_state;
end
// Output logic
// assign out = (state == ...);
assign out = (state==A)? 1'b0:1'b1;
endmodule
2.提交结果
Success
3.题目分析
This is a Moore state machine with two states, one input, and one output. Implement this state machine. Notice that the reset state is B.
This exercise is the same as fsm1s, but using asynchronous reset.

本题引导我们用了个三段式的。
一段式:在一个时序电路完成所有工作。
两段式:时序逻辑电路实现状态转移,组合逻辑电路明确下一状态及输出。
三段式:时序逻辑电路实现状态转移,组合逻辑电路1 明确下一状态,组合逻辑电路2 明确输出。(私以为对此题用三段式最简单。)
**注意:**如果想用两段式,需要将out赋值为“当前状态下的输出”,而非“下一状态对应的输出”。因为这里是连续赋值,当状态由时序逻辑转移到下一状态时,自然会对应上应有的输出。
改动不大:
module top_module(
input clk,
input areset, // Asynchronous reset to state B
input in,
output out);//
parameter A=0, B=1;
reg state, next_state;
always @(*) begin // This is a combinational always block
// State transition logic
case(state)
A: begin
out = 1'b0;
if(in==1'b1) begin
// out = 1'b0;
next_state = A;
end
else begin
// out = 1'b0;
next_state = B;
end
end
B: begin
out = 1'b1;
if(in==1'b1) begin
// out = 1'b1;
next_state = B;
end
else begin
// out = 1'b1;
next_state = A;
end
end
endcase
end
always @(posedge clk, posedge areset) begin // This is a sequential always block
// State flip-flops with asynchronous reset
if(areset)
state <= B;
else
state <= next_state;
end
// Output logic
// assign out = (state == ...);
// assign out = (state==A)? 1'b0:1'b1;
endmodule
II FSM 1 (synchronous reset) (Fsm1s)
1.代码编写
// Note the Verilog-1995 module declaration syntax here:
module top_module(clk, reset, in, out);
input clk;
input reset; // Synchronous reset to state B
input in;
output out;//
reg out;
// Fill in state name declarations
reg present_state, next_state;
parameter A = 1'b1,B = 1'b0;
always @(posedge clk) begin
if (reset) begin
// Fill in reset logic
present_state = B; // 可以是 <=
out <= 1'b1;
end else begin
case (present_state)
// Fill in state transition logic
A: begin
if(in == 1'b1) begin
next_state = A;
end
else begin
next_state = B;
end
end
B: begin
if(in == 1'b1) begin
next_state = B;
end
else begin
next_state = A;
end
end
endcase
// State flip-flops
present_state = next_state;// 必须是阻塞,需因此判断此时的out
case (present_state)
// Fill in output logic
A: out = 1'b0;
B: out = 1'b1;
endcase
end
end
endmodule
2.提交结果
Success
3.题目分析
This is a Moore state machine with two states, one input, and one output. Implement this state machine. Notice that the reset state is B.
This exercise is the same as fsm1, but using synchronous reset.
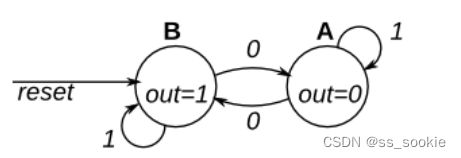
这是一个一段式状态机,注意next_state赋值的时候不要用阻塞赋值,否则延迟一个周期改变状态就乱了。
这里全部用了阻塞赋值 \color{plum}\textbf{这里全部用了阻塞赋值} 这里全部用了阻塞赋值
用一段式来写就很麻烦(阻塞非阻塞),不推荐。 \color{plum}\textbf{用一段式来写就很麻烦(阻塞非阻塞),不推荐。} 用一段式来写就很麻烦(阻塞非阻塞),不推荐。
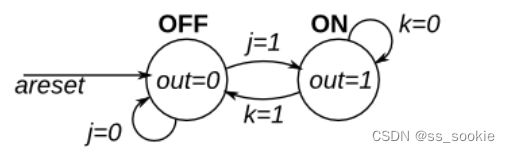
III FSM 2 (asynchronous reset) (Fsm2)
1.代码编写
module top_module(
input clk,
input areset, // Asynchronous reset to OFF
input j,
input k,
output out); //
parameter OFF=0, ON=1;
reg state, next_state;
always @(*) begin
// State transition logic
case(state)
OFF: begin
if(j==1'b0)
next_state = OFF;
else
next_state = ON;
end
ON: begin
if(k==1'b0)
next_state = ON;
else
next_state = OFF;
end
default: next_state = next_state;
endcase
end
always @(posedge clk, posedge areset) begin
// State flip-flops with asynchronous reset
if(areset)
state <= OFF;
else
state <= next_state;
end
// Output logic
// assign out = (state == ...);
assign out = (state == OFF)? 1'b0:1'b1;
endmodule
2.提交结果
Success
3.题目分析
This is a Moore state machine with two states, two inputs, and one output. Implement this state machine.
This exercise is the same as fsm2s, but using asynchronous reset.
IV FSM 2 (synchronous reset) (sm2s)
1.代码编写
module top_module(
input clk,
input reset, // Synchronous reset to OFF
input j,
input k,
output out); //
parameter OFF=0, ON=1;
reg state, next_state;
always @(*) begin
// State transition logic
case(state)
OFF: begin
if(j==1'b0)
next_state = OFF;
else
next_state = ON;
end
ON: begin
if(k==1'b0)
next_state = ON;
else
next_state = OFF;
end
default: next_state = next_state;
endcase
end
always @(posedge clk) begin
// State flip-flops with synchronous reset
if(reset)
state = OFF;
else
state = next_state;
end
// Output logic
// assign out = (state == ...);
assign out = state;
endmodule
2.提交结果
Success
3.题目分析
This is a Moore state machine with two states, two inputs, and one output. Implement this state machine.
This exercise is the same as fsm2, but using synchronous reset.

V Simple State transitions 3 (Fsm3comb)
1.代码编写
module top_module(
input in,
input [1:0] state,
output [1:0] next_state,
output out); //
parameter A=0, B=1, C=2, D=3;
// State transition logic: next_state = f(state, in)
// Output logic: out = f(state) for a Moore state machine
always@(*) begin
case(state)
A: begin
next_state = (in)? B:A;
end
B: begin
next_state = (in)? B:C;
end
C: begin
next_state = (in)? D:A;
end
D: begin
next_state = (in)? B:C;
end
endcase
end
always@(*) begin
case(state)
A: out = 1'b0;
B: out = 1'b0;
C: out = 1'b0;
D: out = 1'b1;
endcase
end
endmodule
2.提交结果
Success
3.题目分析
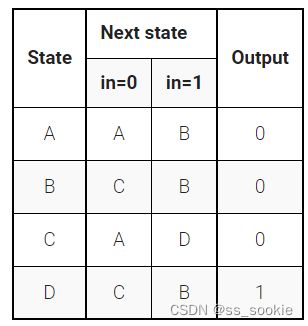
The following is the state transition table for a Moore state machine with one input, one output, and four states. Use the following state encoding: A=2’b00, B=2’b01, C=2’b10, D=2’b11.
Implement only the state transition logic and output logic (the combinational logic portion) for this state machine. Given the current state (state), compute the next_state and output (out) based on the state transition table.
VI Simple one-hot State transitions 3 (Fsm3onehot)
1.代码编写
module top_module(
input in,
input [3:0] state,
output [3:0] next_state,
output out); //
parameter A=0, B=1, C=2, D=3;
// State transition logic: Derive an equation for each state flip-flop.
assign next_state[A] = state[0]&~in|state[2]&~in;
assign next_state[B] = state[0]&in|state[1]&in|state[3]∈
assign next_state[C] = state[1]&~in|state[3]&~in;
assign next_state[D] = state[2]∈
// Output logic:
assign out = state[3];
endmodule
2.提交结果
Success
3.题目分析
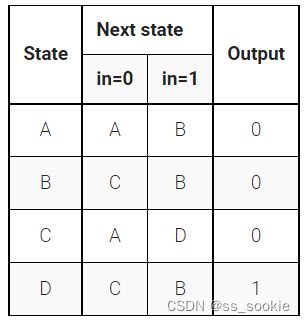
The following is the state transition table for a Moore state machine with one input, one output, and four states. Use the following one-hot state encoding: A=4’b0001, B=4’b0010, C=4’b0100, D=4’b1000.
Derive state transition and output logic equations by inspection assuming a one-hot encoding. Implement only the state transition logic and output logic (the combinational logic portion) for this state machine. (The testbench will test with non-one hot inputs to make sure you’re not trying to do something more complicated).
What does “derive equations by inspection” mean?
One-hot state machine encoding guarantees that exactly one state bit is 1. This means that it is possible to determine whether the state machine is in a particular state by examining only one state bit, not all state bits. This leads to simple logic equations for the state transitions by examining the incoming edges for each state in the state transition diagram.
For example, in the above state machine, how can the state machine can reach state A? It must use one of the two incoming edges: “Currently in state A and in=0” or “Currently in state C and in = 0”. Due to the one-hot encoding, the logic equation to test for “currently in state A” is simply the state bit for state A. This leads to the final logic equation for the next state of state bit A: next_state[0] = state[0]&(~in) | state[2]&(~in). The one-hot encoding guarantees that at most one clause (product term) will be “active” at a time, so the clauses can just be ORed together.
When an exercise asks for state transition equations “by inspection”, use this particular method. The judge will test with non-one-hot inputs to ensure your logic equations follow this method, rather that doing something else (such as resetting the FSM) for illegal (non-one-hot) combinations of the state bits.
Although knowing this algorithm isn’t necessary for RTL-level design (the logic synthesizer handles this), it is illustrative of why one-hot FSMs often have simpler logic (at the expense of more state bit storage), and this topic frequently shows up on exams in digital logic courses.
这里用的独热码,仅有一位是1,所以 next_state,out 都是 state 是 1 的那些位与 in 的逻辑表达式,无需兼顾非 1 的位。
VII Simple FSM 3 (asynchronous reset) (fsm3)
1.代码编写
module top_module(
input clk,
input in,
input areset,
output out); //
parameter A = 2'b00 , B = 2'b01 , C = 2'b10 , D = 2'b11;
reg [1:0] state,next_state;
// State transition logic
always@(*) begin
case(state)
A: begin
next_state = (in)? B:A;
end
B: begin
next_state = (in)? B:C;
end
C: begin
next_state = (in)? D:A;
end
D: begin
next_state = (in)? B:C;
end
endcase
end
// State flip-flops with asynchronous reset
always@(posedge clk,posedge areset) begin
if(areset)
state <= A;
else
state <= next_state;
end
// Output logic
assign out = (state == D)? 1'b1:1'b0;
endmodule
2.提交结果
Success
3.题目分析
See also: State transition logic for this FSM
The following is the state transition table for a Moore state machine with one input, one output, and four states. Implement this state machine. Include an asynchronous reset that resets the FSM to state A.
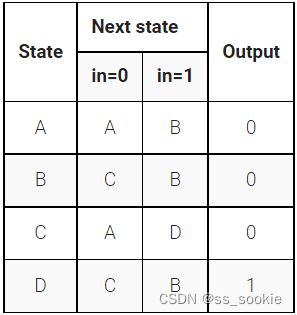
三段式 正常写。
VIII Simple FSM 3 (synchronous reset) (Fsm3s)
1.代码编写
module top_module(
input clk,
input in,
input reset,
output out); //
parameter A = 2'b00 , B = 2'b01 , C = 2'b10 , D = 2'b11;
reg [1:0] state,next_state;
// State transition logic
always@(*) begin
case(state)
A: begin
next_state = (in)? B:A;
end
B: begin
next_state = (in)? B:C;
end
C: begin
next_state = (in)? D:A;
end
D: begin
next_state = (in)? B:C;
end
endcase
end
// State flip-flops with asynchronous reset
always@(posedge clk) begin
if(reset)
state <= A;
else
state <= next_state;
end
// Output logic
assign out = (state == D)? 1'b1:1'b0;
endmodule
2.提交结果
3.题目分析
See also: State transition logic for this FSM
The following is the state transition table for a Moore state machine with one input, one output, and four states. Implement this state machine. Include a synchronous reset that resets the FSM to state A. (This is the same problem as Fsm3 but with a synchronous reset.)
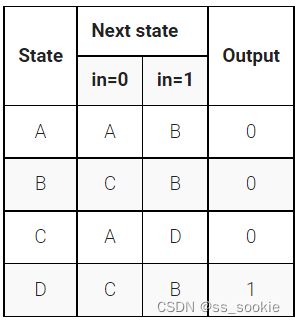
三段式,把上一题 时序逻辑 模块的 posedge areset 去掉即可。
IX Design a moore FSM(Exams/ece241 2013 q4)
1.代码编写
module top_module (
input clk,
input reset,
input [3:1] s,
output fr3,
output fr2,
output fr1,
output dfr
);
reg [1:0] state , next_state;
parameter b1 = 2'b00 , u1b2 = 2'b01 , u2b3 = 2'b10 , u3 = 2'b11; // 水位越高,状态值也越大。
always@(posedge clk) begin
if(reset)
state <= b1;
else
state <= next_state;
end
always@(*) begin
case(s) //根据传感器的输入判定水箱下一个状态
3'b000: next_state = b1;
3'b001: next_state = u1b2;
3'b011: next_state = u2b3;
3'b111: next_state = u3;
default: next_state = b1;
endcase
end
always@(posedge clk) begin
if(reset)
{fr3,fr2,fr1,dfr} <= 4'b1111;// dfr <= 1'b1; 不可,因为fr123 是依靠s赋值而非依靠 state赋值
else begin
case(s)
3'b000: {fr3,fr2,fr1} <= 3'b111;
3'b001: {fr3,fr2,fr1} <= 3'b011;
3'b011: {fr3,fr2,fr1} <= 3'b001;
3'b111: {fr3,fr2,fr1} <= 3'b000;
endcase
if(state < next_state)
dfr <= 1'b0;
else if(state > next_state) //一开始这里直接else了
dfr <= 1'b1;
else
dfr <= dfr;
end
end
endmodule
2.提交结果
Success
3.题目分析
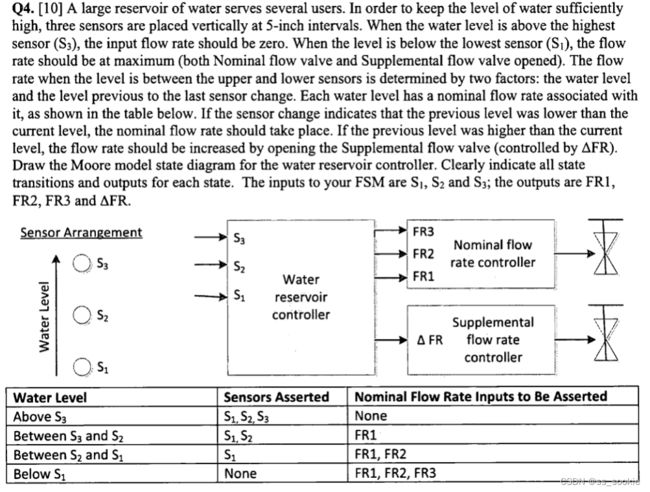
Also include an active-high synchronous reset that resets the state machine to a state equivalent to if the water level had been low for a long time (no sensors asserted, and all four outputs asserted).
有这样一个储水系统:
- 当水量在传感器S3以上时,输入流量最小(nominal和supplemental均为0).
- 当储水量在传感器S1以下时,输入流量最大(nominal和supplemental全打开,均为1).
- 当储水量在S1~S3之间时,输入流量与“上一状态和此状态的储水量大小关系”有关。每一个储水量与nominal flow rate有表格中的关系。 当上一状态储水量大于这一状态时,将触发nominal flow rate。当上一状态储水量小于这一状态时,还需打开supplemental flow rate controller 以增加水流。
- 高电平触发、同步置位,当置位时,状态为“水量在S1以下”,且“4个输出全都打开(nominal和supplemental全都打开)”。
代码中有一些需要注意的地方(见注释)
module top_module (
input clk,
input reset,
input [3:1] s,
output fr3,
output fr2,
output fr1,
output dfr
);
reg [1:0] state , next_state;
parameter b1 = 2'b00 , u1b2 = 2'b01 , u2b3 = 2'b10 , u3 = 2'b11; // 水位越高,状态值也越大。
always@(posedge clk) begin
if(reset)
state <= b1;
else
state <= next_state;
end
always@(*) begin
case(s) //根据传感器的输入判定水箱下一个状态
3'b000: next_state = b1;
3'b001: next_state = u1b2;
3'b011: next_state = u2b3;
3'b111: next_state = u3;
default: next_state = b1;
endcase
end
always@(posedge clk) begin // 这里用时序逻辑
// 因为这里用的是state 和 next_state,而题中要求用previous_state和state。
// case里用来判断的是s,对应了next_state的状态,又因为在状态转移模块用的就是时序逻辑,只有当这一周期末(下一周期初),state\next_state分别变为previous_state\state时,产生对应的输出(fr3,fr2,fr1,dfr)才可以。
if(reset)
{fr3,fr2,fr1,dfr} <= 4'b1111;// 之前写成了dfr <= 1'b1; 不可,因为fr123 是依靠s赋值而非依靠 state赋值
else begin
case(s)
3'b000: {fr3,fr2,fr1} <= 3'b111;
3'b001: {fr3,fr2,fr1} <= 3'b011;
3'b011: {fr3,fr2,fr1} <= 3'b001;
3'b111: {fr3,fr2,fr1} <= 3'b000;
endcase
if(state < next_state)
dfr <= 1'b0;
else if(state > next_state) //一开始这里直接else了,后来根据报错波形猜测出题人认为当水量不变时,dfr维持原输出。
dfr <= 1'b1;
else
dfr <= dfr;
end
end
endmodule
X Lemmings 1
1.代码编写
module top_module(
input clk,
input areset, // Freshly brainwashed Lemmings walk left.
input bump_left,
input bump_right,
output walk_left,
output walk_right); //
parameter LEFT=0, RIGHT=1;
reg state, next_state;
always @(*) begin
// State transition logic
case(state)
LEFT: begin
if(bump_left)
next_state = RIGHT;
else
next_state = LEFT;
end
RIGHT: begin
if(bump_right)
next_state = LEFT;
else
next_state = RIGHT;
end
endcase
end
always @(posedge clk, posedge areset) begin
// State flip-flops with asynchronous reset
if(areset)
state <= LEFT;
else
state <= next_state;
end
// Output logic
assign walk_left = (state == LEFT)? 1'b1:1'b0;
assign walk_right = (state == RIGHT)? 1'b1:1'b0;
endmodule
2.提交结果
Success
3.题目分析
The game Lemmings involves critters with fairly simple brains. So simple that we are going to model it using a finite state machine.
In the Lemmings’ 2D world, Lemmings can be in one of two states: walking left or walking right. It will switch directions if it hits an obstacle. In particular, if a Lemming is bumped on the left, it will walk right. If it’s bumped on the right, it will walk left. If it’s bumped on both sides at the same time, it will still switch directions.
Implement a Moore state machine with two states, two inputs, and one output that models this behaviour.
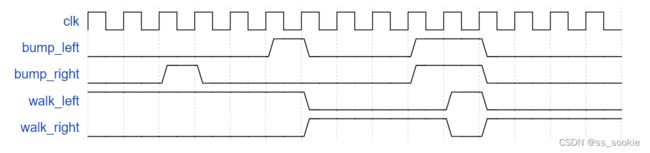
See also: Lemmings2, Lemmings3, and Lemmings4.
仔细读题
XI Lemmings2
1.代码编写
module top_module(
input clk,
input areset, // Freshly brainwashed Lemmings walk left.
input bump_left,
input bump_right,
input ground,
output walk_left,
output walk_right,
output aaah );
reg [1:0] state,next_state;
parameter LEFT = 2'b00,RIGHT = 2'b01,AHLEFT = 2'b11,AHRIGHT = 2'b10;
always@(*) begin
case(state)
LEFT: begin
if(!ground)
next_state = AHLEFT;
else if(!bump_left)
next_state = LEFT;
else
next_state = RIGHT;
end
RIGHT: begin
if(!ground)
next_state = AHRIGHT;
else if(!bump_right)
next_state = RIGHT;
else
next_state = LEFT;
end
AHLEFT: begin
if(!ground)
next_state = AHLEFT;
else
next_state = LEFT;
end
AHRIGHT: begin
if(!ground)
next_state = AHRIGHT;
else
next_state = RIGHT;
end
endcase
end
always@(posedge clk,posedge areset) begin
if(areset)
state <= LEFT;
else
state <= next_state;
end
assign walk_left = (state == LEFT)? 1'b1:1'b0;
assign walk_right = (state == RIGHT)? 1'b1:1'b0;
assign aaah = (state == AHLEFT || state == AHRIGHT)? 1'b1:1'b0;
endmodule
2.提交结果
Success
3.题目分析
See also: Lemmings1.
In addition to walking left and right, Lemmings will fall (and presumably go “aaah!”) if the ground disappears underneath them.
In addition to walking left and right and changing direction when bumped, when ground=0, the Lemming will fall and say “aaah!”. When the ground reappears (ground=1), the Lemming will resume walking in the same direction as before the fall. Being bumped while falling does not affect the walking direction, and being bumped in the same cycle as ground disappears (but not yet falling), or when the ground reappears while still falling, also does not affect the walking direction.
Build a finite state machine that models this behaviour.
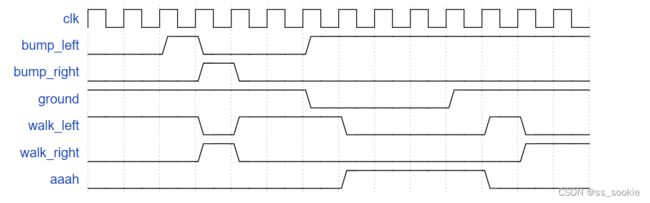
See also: Lemmings3 and Lemmings4.
是异步置位,直接用状态“向左掉落”,“向右掉落”,而无需再设一个“previous_state”(原来的思路)。
XII Lemmings3
1.代码编写
module top_module(
input clk,
input areset, // Freshly brainwashed Lemmings walk left.
input bump_left,
input bump_right,
input ground,
input dig,
output walk_left,
output walk_right,
output aaah,
output digging );
reg [2:0] state,next_state;
parameter LEFT = 3'b000 , RIGHT = 3'b001 , DLEFT = 3'b010 , DRIGHT = 3'b011 , FLEFT = 3'b100 , FRIGHT = 3'b101;
always@(*) begin
case(state)
LEFT: begin
if(!ground)
next_state = FLEFT; //high precedence
else if(dig)
next_state = DLEFT;
else if(bump_left)
next_state = RIGHT;
else
next_state = LEFT;
end
RIGHT: begin
if(!ground)
next_state = FRIGHT; //high precedence
else if(dig)
next_state = DRIGHT;
else if(bump_right)
next_state = LEFT;
else
next_state = RIGHT;
end
DLEFT: begin
if(!ground)
next_state = FLEFT;
else
next_state = DLEFT;
end
DRIGHT: begin
if(!ground)
next_state = FRIGHT;
else
next_state = DRIGHT;
end
FLEFT: begin
if(!ground)
next_state = FLEFT;
else
next_state = LEFT;
end
FRIGHT: begin
if(!ground)
next_state = FRIGHT;
else
next_state = RIGHT;
end
endcase
end
always@(posedge clk,posedge areset) begin
if(areset)
state <= LEFT;
else
state <= next_state;
end
assign walk_left = (state == LEFT)? 1'b1:1'b0;
assign walk_right = (state == RIGHT)? 1'b1:1'b0;
assign aaah = (state == FLEFT || state == FRIGHT )? 1'b1:1'b0;
assign digging = (state == DLEFT || state == DRIGHT)? 1'b1:1'b0;
endmodule
2.提交结果
Success
3.题目分析
See also: Lemmings1 and Lemmings2.
In addition to walking and falling, Lemmings can sometimes be told to do useful things, like dig (it starts digging when dig=1). A Lemming can dig if it is currently walking on ground (ground=1 and not falling), and will continue digging until it reaches the other side (ground=0). At that point, since there is no ground, it will fall (aaah!), then continue walking in its original direction once it hits ground again. As with falling, being bumped while digging has no effect, and being told to dig when falling or when there is no ground is ignored.
(In other words, a walking Lemming can fall, dig, or switch directions. If more than one of these conditions are satisfied, fall has higher precedence than dig, which has higher precedence than switching directions.)
Extend your finite state machine to model this behaviour.
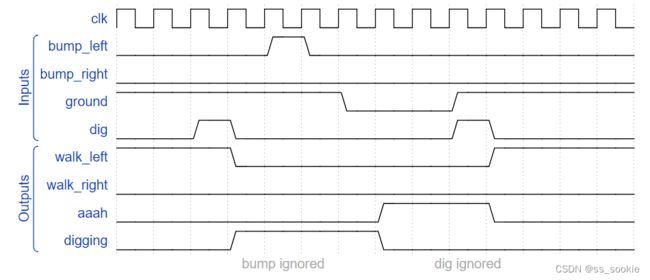
Hint: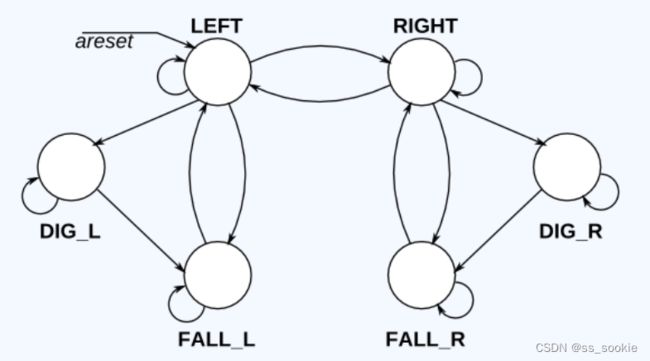
像上一道题,分别设置不同方向的 FALL,不同方向的 DIG即可,编程的时候按照优先级排序,还挺清晰的。
XIII Lemmings4
1.代码编写
module top_module(
input clk,
input areset, // Freshly brainwashed Lemmings walk left.
input bump_left,
input bump_right,
input ground,
input dig,
output walk_left,
output walk_right,
output aaah,
output digging );
reg [4:0] counter;
reg [2:0] state,next_state;
parameter LEFT = 3'b000 , RIGHT = 3'b001 , DLEFT = 3'b010 , DRIGHT = 3'b011 , FLEFT = 3'b100 , FRIGHT = 3'b101 , SPLATTER = 3'b110;
always@(*) begin
case(state)
LEFT: begin
if(!ground)
next_state = FLEFT; //high precedence
else if(dig)
next_state = DLEFT;
else if(bump_left)
next_state = RIGHT;
else
next_state = LEFT;
end
RIGHT: begin
if(!ground)
next_state = FRIGHT; //high precedence
else if(dig)
next_state = DRIGHT;
else if(bump_right)
next_state = LEFT;
else
next_state = RIGHT;
end
DLEFT: begin
if(!ground)
next_state = FLEFT;
else
next_state = DLEFT;
end
DRIGHT: begin
if(!ground)
next_state = FRIGHT;
else
next_state = DRIGHT;
end
FLEFT: begin
if(!ground)
next_state = FLEFT;
else if(counter == 5'd20)
next_state = SPLATTER;
else
next_state = LEFT;
end
FRIGHT: begin
if(!ground)
next_state = FRIGHT;
else if(counter == 5'd20)
next_state = SPLATTER;
else
next_state = RIGHT;
end
SPLATTER: begin
next_state = SPLATTER;
end
endcase
end
always@(posedge clk,posedge areset) begin //state transfer
if(areset)
state <= LEFT;
else
state <= next_state;
end
always@(posedge clk,posedge areset) begin // count up
if(areset)
counter <= 5'd0;
else if(state == FLEFT || state == FRIGHT) //Falling
counter <= (counter == 5'd20)? counter:counter + 5'd1;
else //not Falling
counter <= 5'd0;
end
assign walk_left = (state == LEFT)? 1'b1:1'b0;
assign walk_right = (state == RIGHT)? 1'b1:1'b0;
assign aaah = (state == FLEFT || state == FRIGHT)? 1'b1:1'b0;
assign digging = (state == DLEFT || state == DRIGHT)? 1'b1:1'b0; // SPLATTER不是其中任何一个状态,所以无需特殊赋值
endmodule
2.提交结果
Success
3.题目分析
See also: Lemmings1, Lemmings2, and Lemmings3.
Although Lemmings can walk, fall, and dig, Lemmings aren’t invulnerable. If a Lemming falls for too long then hits the ground, it can splatter. In particular, if a Lemming falls for more than 20 clock cycles then hits the ground, it will splatter and cease walking, falling, or digging (all 4 outputs become 0), forever (Or until the FSM gets reset). There is no upper limit on how far a Lemming can fall before hitting the ground. Lemmings only splatter when hitting the ground; they do not splatter in mid-air.
Extend your finite state machine to model this behaviour.
Falling for 20 cycles is survivable:
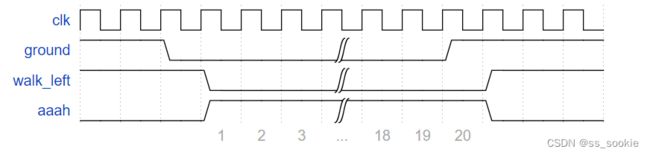
Falling for 21 cycles causes splatter:
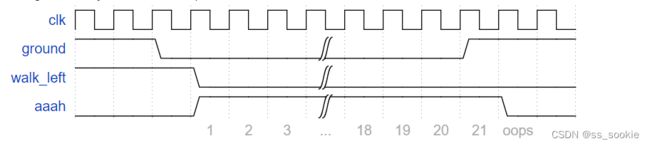
可见,在 fall 的第19个周期出现ground,不会splatter;在 fall 的第20个周期开始,出现ground,才会splatter,所以counter卡5’d20。
XIV One-hot FSM
1.代码编写
module top_module(
input in,
input [9:0] state,
output [9:0] next_state,
output out1,
output out2);
parameter [9:0] S0 = 10'b0000_0000_01,S1 = 10'b0000_0000_10,S2 = 10'b0000_0001_00,S3 = 10'b0000_0010_00,S4 = 10'b0000_0100_00;
parameter [9:0] S5 = 10'b0000_1000_00,S6 = 10'b0001_0000_00,S7 = 10'b0010_0000_00,S8 = 10'b0100_0000_00,S9 = 10'b1000_0000_00;
assign next_state[0] = ~in&(state[0]|state[1]|state[2]|state[3]|state[4]|state[7]|state[8]|state[9]);
assign next_state[1] = in&(state[0]|state[8]|state[9]);
assign next_state[2] = in&state[1];
assign next_state[3] = in&state[2];
assign next_state[4] = in&state[3];
assign next_state[5] = in&state[4];
assign next_state[6] = in&state[5];
assign next_state[7] = in&(state[6]|state[7]);
assign next_state[8] = ~in&state[5];
assign next_state[9] = ~in&state[6];
assign out1 = state[8]|state[9];
assign out2 = state[7]|state[9];
endmodule
2.提交结果
Success
3.题目分析
Given the following state machine with 1 input and 2 outputs:
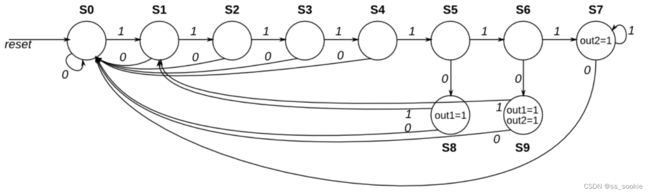
Suppose this state machine uses one-hot encoding, where state[0] through state[9] correspond to the states S0 though S9, respectively. The outputs are zero unless otherwise specified.
Implement the state transition logic and output logic portions of the state machine (but not the state flip-flops). You are given the current state in state[9:0] and must produce next_state[9:0] and the two outputs. Derive the logic equations by inspection assuming a one-hot encoding. (The testbench will test with non-one hot inputs to make sure you’re not trying to do something more complicated).
指出了,只需要实现状态转移模块与输出模块,不用实现触发器。
应用独热码的性质,直接组合赋值即可。
Hint:Logic equations for one-hot state transition logic can be derived by looking at in-edges of the state transition diagram.
独热码的状态转移,可以仅通过观察状态转移图的输入边来实现。
不同的“1”位,代表不同的state。
XV PS/2 packet parser
1.代码编写
module top_module(
input clk,
input [7:0] in,
input reset, // Synchronous reset
output done); //
reg [1:0] state,next_state;
parameter [1:0] search_1 = 2'b00,search_2 = 2'b01,search_3 = 2'b11,DONE = 2'b10;
// State transition logic (combinational)
always@(*) begin
case(state)
search_1: begin
next_state = (in[3])? search_2:search_1;
end
search_2: begin
next_state = search_3;
end
search_3: begin
next_state = DONE;
end
DONE: begin
next_state = (in[3])? search_2:search_1;
end
default: next_state = search_1;
endcase
end
// State flip-flops (sequential)
always@(posedge clk) begin
if(reset)
state <= search_1;
else
state <= next_state;
end
// Output logic
assign done = (state == DONE)? 1'b1:1'b0;
endmodule
2.提交结果
Success
3.题目分析
The PS/2 mouse protocol sends messages that are three bytes long. However, within a continuous byte stream, it’s not obvious where messages start and end. The only indication is that the first byte of each three byte message always has bit[3]=1 (but bit[3] of the other two bytes may be 1 or 0 depending on data).
We want a finite state machine that will search for message boundaries when given an input byte stream. The algorithm we’ll use is to discard bytes until we see one with bit[3]=1. We then assume that this is byte 1 of a message, and signal the receipt of a message once all 3 bytes have been received (done).
The FSM should signal done in the cycle immediately after the third byte of each message was successfully received.
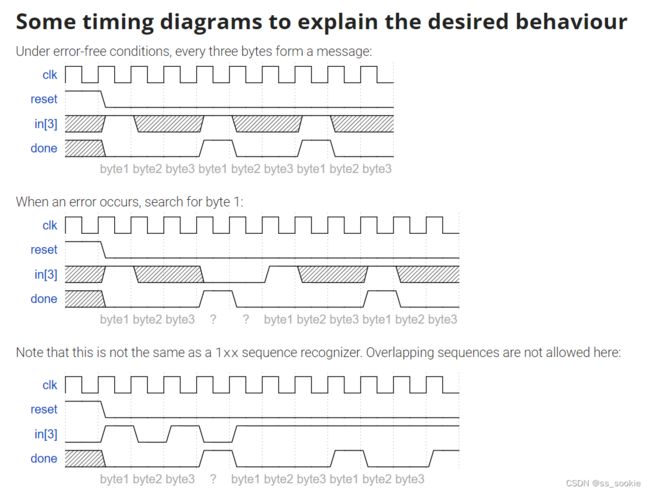
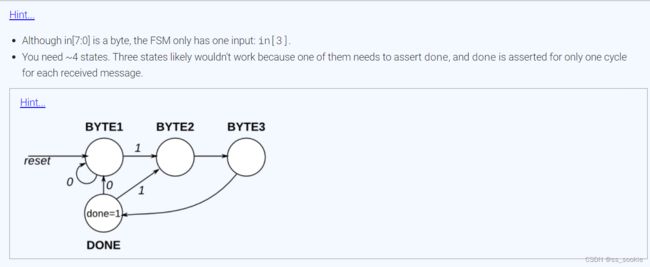
不如将状态BYTE1,BYTE2.BYTE3理解为‘search for Byte1(Byte2/Byte3)’,当收到in[3]=1,代表收到了Byte1,转而搜寻第2、3个字节。
XVI PS/2 packet parser and datapass
1.代码编写
module top_module(
input clk,
input [7:0] in,
input reset, // Synchronous reset
output [23:0] out_bytes,
output done); //
reg [1:0] state,next_state;
parameter [1:0] search_1 = 2'b00,search_2 = 2'b01,search_3 = 2'b11,DONE = 2'b10;
// FSM from fsm_ps2
always@(*) begin
case(state)
search_1: begin
next_state = (in[3])? search_2:search_1;
end
search_2: begin
next_state = search_3;
end
search_3: begin
next_state = DONE;
end
DONE: begin
next_state = (in[3])? search_2:search_1;
end
default: next_state = search_1;
endcase
end
// State flip-flops (sequential)
always@(posedge clk) begin
if(reset)
state <= search_1;
else
state <= next_state;
end
// Output logic
assign done = (state == DONE)? 1'b1:1'b0;
// New: Datapath to store incoming bytes.
always@(posedge clk) begin
if(reset)
out_bytes <= 24'd0;
else
out_bytes <= {out_bytes[15:0],in}; //24位,逻辑左移,在低位补充in。
end
endmodule
2.提交结果
Success
3.题目分析
See also: PS/2 packet parser.
Now that you have a state machine that will identify three-byte messages in a PS/2 byte stream, add a datapath that will also output the 24-bit (3 byte) message whenever a packet is received (out_bytes[23:16] is the first byte, out_bytes[15:8] is the second byte, etc.).
out_bytes needs to be valid whenever the done signal is asserted. You may output anything at other times (i.e., don’t-care).
For example:

**Hint:**需要读取出Byte1~Byte3,并且只对DONE状态下输出感兴趣,这只需要有一个拼接数据的操作,即每三个连续的字节都被记录,知识DONE状态下被读出即可。
之前还想了一大堆条件,什么时候开始记录,什么时候输出0,太麻烦了,学习到了好方法,真棒!
XVII Serial receiver (Fsm serial)
1.代码编写
module top_module(
input clk,
input in,
input reset, // Synchronous reset
output done
);
reg [3:0] cnt;
reg [2:0] state,next_state;
parameter [2:0] IDLE = 3'd1,START = 3'd2,DATA = 3'd3,DONE = 3'd4,ERROR = 3'd5;
// state transfer
always@(*) begin
case(state)
IDLE: begin
next_state = (in)? IDLE:START;
end
START: begin
next_state = DATA;
end
DATA: begin
if(cnt == 4'd8) begin
next_state = (in)? DONE:ERROR;
end
else begin
next_state = DATA;
end
end
DONE: begin
next_state = (in)? IDLE:START;
end
ERROR: begin
next_state = (in)? IDLE:ERROR;
end
default: next_state = IDLE;
endcase
end
// flip-flops & counter
always@(posedge clk) begin
if(reset) begin
state <= IDLE;
cnt <= 4'd0;
done <= 1'd0;
end
else begin
state <= next_state;
case(next_state)
DATA: begin
cnt <= cnt+4'd1;
done <= 1'b0;
end
DONE: begin
cnt <= 4'd0;
done <= 1'b1;
end
IDLE: begin
cnt <= 4'd0;
done <= 1'b0;
end
START: begin
cnt <= 4'd0;
done <= 1'b0;
end
default: begin
cnt <= 4'd0;
done <= 1'b0;
end
endcase
end
end
endmodule
2.提交结果
Success
3.题目分析
In many (older) serial communications protocols, each data byte is sent along with a start bit and a stop bit, to help the receiver delimit bytes from the stream of bits. One common scheme is to use one start bit (0), 8 data bits, and 1 stop bit (1). The line is also at logic 1 when nothing is being transmitted (idle).
Design a finite state machine that will identify when bytes have been correctly received when given a stream of bits. It needs to identify the start bit, wait for all 8 data bits, then verify that the stop bit was correct. If the stop bit does not appear when expected, the FSM must wait until it finds a stop bit before attempting to receive the next byte.
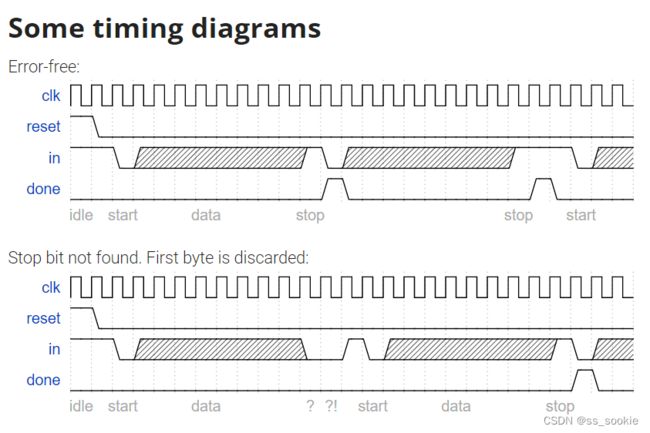
可以做出状态转移图:
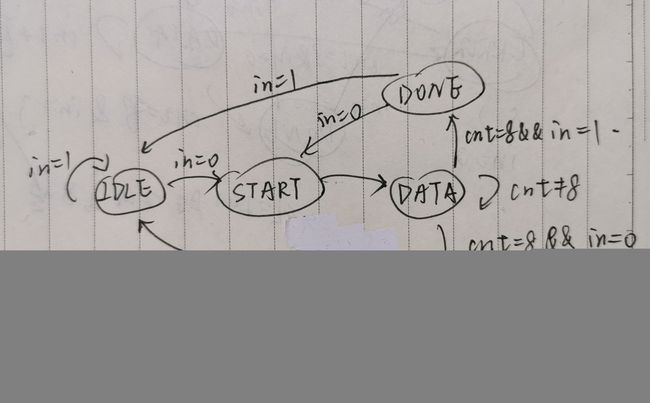
另,这里是由next_state来代替state的(next_state的名字才是当前state下比特的名字),所以,在之后的计数、赋值输出模块中,用next_state作为条件来代替state做条件即可得到正确输出。
XVIII Serial receiver and datapath
1.代码编写
module top_module(
input clk,
input in,
input reset, // Synchronous reset
output [7:0] out_byte,
output done
); //
reg [3:0] cnt;
reg [2:0] state,next_state;
parameter [2:0] IDLE = 3'd1,START = 3'd2,DATA = 3'd3,DONE = 3'd4,ERROR = 3'd5;
// Use FSM from Fsm_serial
// state transfer
always@(*) begin
case(state)
IDLE: begin
next_state = (in)? IDLE:START;
end
START: begin
next_state = DATA;
end
DATA: begin
if(cnt == 4'd8) begin
next_state = (in)? DONE:ERROR;
end
else begin
next_state = DATA;
end
end
DONE: begin
next_state = (in)? IDLE:START;
end
ERROR: begin
next_state = (in)? IDLE:ERROR;
end
default: next_state = IDLE;
endcase
end
// flip-flops & counter
always@(posedge clk) begin
if(reset) begin
state <= IDLE;
cnt <= 4'd0;
done <= 1'd0;
end
else begin
state <= next_state;
case(next_state)
DATA: begin
cnt <= cnt+4'd1;
done <= 1'b0;
end
DONE: begin
cnt <= 4'd0;
done <= 1'b1;
end
IDLE: begin
cnt <= 4'd0;
done <= 1'b0;
end
START: begin
cnt <= 4'd0;
done <= 1'b0;
end
default: begin
cnt <= 4'd0;
done <= 1'b0;
end
endcase
end
end
// New: Datapath to latch input bits.
always@(posedge clk) begin
if(reset)
out_byte <= 8'd0;
else
out_byte <= (next_state == DATA)? {in,out_byte[7:1]}:out_byte;
end
endmodule
2.提交结果
Success
3.题目分析
See also: Serial receiver
Now that you have a finite state machine that can identify when bytes are correctly received in a serial bitstream, add a datapath that will output the correctly-received data byte. out_byte needs to be valid when done is 1, and is don’t-care otherwise.
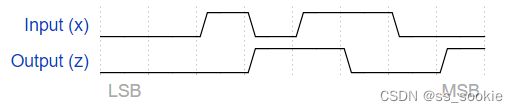
Note that the serial protocol sends the least significant bit first.
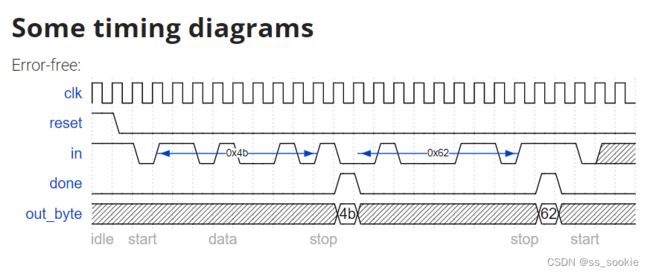
Hint:The serial bitstream needs to be shifted in one bit at a time, then read out in parallel.
只需要在上一道题的基础上加上New: Datapath to latch input bits.部分。这也不用过于复杂,只要进行实时存储即可,只是这里只要输出Data数据,所以不应记录start和stop。理由和上一题一样,状态机的状态是延迟了一个时钟周期的,判断时要用next_state,且当next_state!=DATA时,应选择 保持输出 而非 归零,因为next_state==DATA和读取out_byte之间还需要隔一个next_state = DONE状态,我们需要将输出数据保持,直至读取。
XIX Serial receiver with parity checking
1.代码编写
module top_module(
input clk,
input in,
input reset, // Synchronous reset
output [7:0] out_byte,
output done
); //
reg odd_reset,odd;
reg [3:0] cnt;
reg [2:0] state,next_state;
parameter [2:0] IDLE = 3'd1,START = 3'd2,DATA = 3'd3,DONE = 3'd4,ERROR = 3'd5,PARITY = 3'd0;
// Use FSM from Fsm_serial
// state transfer
always@(*) begin
case(state)
IDLE: begin
next_state = (in)? IDLE:START;
end
START: begin
next_state = DATA;
end
DATA: begin
next_state = (cnt == 4'd8)? PARITY:DATA;
end
PARITY: begin
next_state = (in)? DONE:ERROR;
end
DONE: begin
next_state = (in)? IDLE:START;
end
ERROR: begin
next_state = (in)? IDLE:ERROR;
end
default: next_state = IDLE;
endcase
end
// flip-flops
always@(posedge clk) begin
if(reset)
state <= IDLE;
else
state <= next_state;
end
// counter
always@(posedge clk) begin
if(reset)
cnt <= 4'd0;
else begin
cnt <= (next_state == DATA)? cnt+4'd1:4'd0;
end
end
// New: Datapath to latch input bits.
always@(posedge clk) begin
if(reset)
out_byte <= 8'd0;
else
out_byte <= (next_state == DATA)? {in,out_byte[7:1]}:out_byte;
end
// Modify FSM and datapath from Fsm_serialdata
// instantiate only check when next_state=DATA
parity instance1(.clk(clk),.reset(odd_reset),.in(in),.odd(odd));
//You have to reset parity module when reset\next_state == IDLE
// start bit = 0,it wont influence on parity result;
// odd_reset = 0 when next state = DONE,for odd cant be reset to 0 here
// You have to reset odd when state = START,there odd will be 0 while receiving the 1st DATA bit.
assign odd_reset = reset||(next_state == IDLE)||(next_state == START);
// New: Add parity checking.
always@(posedge clk) begin
done <= (next_state == DONE) && odd; // here it is odd or not ~odd, stop bit ==1 ,but it's too late to influence done. it'll influence the state next to next_state = DONE
end
endmodule
2.提交结果
Success
3.题目分析
See also: Serial receiver and datapath
We want to add parity checking to the serial receiver. Parity checking adds one extra bit after each data byte. We will use odd parity, where the number of 1s in the 9 bits received must be odd. For example, 101001011 satisfies odd parity (there are 5 1s), but 001001011 does not.
Change your FSM and datapath to perform odd parity checking. Assert the done signal only if a byte is correctly received and its parity check passes. Like the serial receiver FSM, this FSM needs to identify the start bit, wait for all 9 (data and parity) bits, then verify that the stop bit was correct. If the stop bit does not appear when expected, the FSM must wait until it finds a stop bit before attempting to receive the next byte.
You are provided with the following module that can be used to calculate the parity of the input stream (It’s a TFF with reset). The intended use is that it should be given the input bit stream, and reset at appropriate times so it counts the number of 1 bits in each byte.
module parity (
input clk,
input reset,
input in,
output reg odd);
always @(posedge clk)
if (reset) odd <= 0;
else if (in) odd <= ~odd;
endmodule
Note that the serial protocol sends the least significant bit first, and the parity bit after the 8 data bits.
Some timing diagrams
No framing errors. Odd parity passes for first byte, fails for second byte.
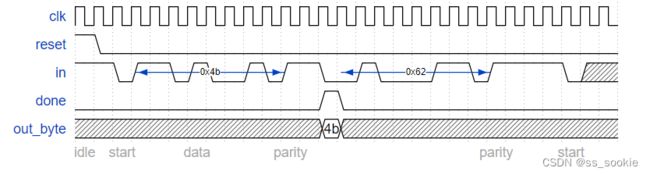
做出状态转移图:

之前犯过一个错误导致一直调不出来,就是代码第 67 行没有加 next_state = START.
当时考虑的是next_state = START状态下收到的in为0,不会影响odd判定结果。
但如若状态为 state = DONE , next_state = START时,in为0不影响odd结果,但odd会保持上一次判别的 odd = 1,所以这里应该使用next_state = START条件,使odd置位,再对DATA进行奇偶校验。
20 Sequence recognition
1.代码编写
module top_module(
input clk,
input reset, // Synchronous reset
input in,
output disc,
output flag,
output err);
reg [3:0] state ,next_state;
parameter [3:0] B1 = 4'd0,B2 = 4'd1,B3 = 4'd2,B4 = 4'd3,B5 = 4'd4,B6 = 4'd5,B7 = 4'd6,FLAG = 4'd7,ERR = 4'd8,DISC = 4'd9;
// state transfer
always@(*) begin
case(state)
B1: begin
next_state = (in)? B2:B1;
end
B2: begin
next_state = (in)? B3:B1;
end
B3: begin
next_state = (in)? B4:B1;
end
B4: begin
next_state = (in)? B5:B1;
end
B5: begin
next_state = (in)? B6:B1;
end
B6: begin
next_state = (in)? B7:DISC;
end
B7: begin
next_state = (in)? ERR:FLAG;
end
FLAG: begin
next_state = (in)? B2:B1;
end
DISC: begin
next_state = (in)? B2:B1;
end
ERR: begin
next_state = (in)? ERR:B1;
end
endcase
end
// flip-flop
always@(posedge clk) begin
if(reset)
state <= B1;
else
state <= next_state;
end
always@(*) begin
flag = (state == FLAG);
disc = (state == DISC);
err = (state == ERR);
end
endmodule
2.提交结果
Success
3.题目分析
Synchronous HDLC framing involves decoding a continuous bit stream of data to look for bit patterns that indicate the beginning and end of frames (packets). Seeing exactly 6 consecutive 1s (i.e., 01111110) is a “flag” that indicate frame boundaries. To avoid the data stream from accidentally containing “flags”, the sender inserts a zero after (在之后插,不是两头插)every 5 consecutive 1s which the receiver must detect and discard. We also need to signal an error if there are 7 or more consecutive 1s.
Create a finite state machine to recognize these three sequences:
0111110: Signal a bit needs to be discarded (disc).
01111110: Flag the beginning/end of a frame (flag).
01111111…: Error (7 or more 1s) (err).
When the FSM is reset, it should be in a state that behaves as though the previous input were 0.
Here are some example sequences that illustrate the desired operation.
Discard 0111110:
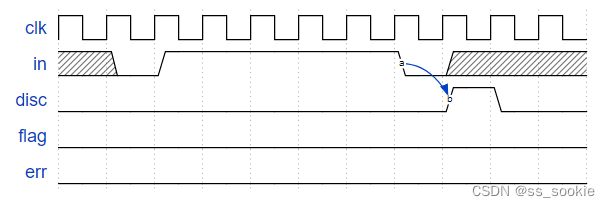
Flag 01111110:

Reset behaviour and error 01111111…:
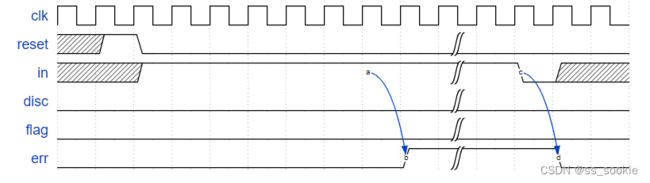
Implement this state machine.
- 当收到 0111110,丢弃这个 为了区别于帧边沿信号而插入的0,disc = 1。(一开始理解错了,以为凡是011111(<=5个1)0,都需要disc=1).
- 当收到01111110,代表信号边沿,flag = 1。
- 当收到01111111(7个及以上1),代表接受错误,err = 1;
- disc\flag\err的值与状态之间是无延迟的。
- 所以得到状态转移图如下:
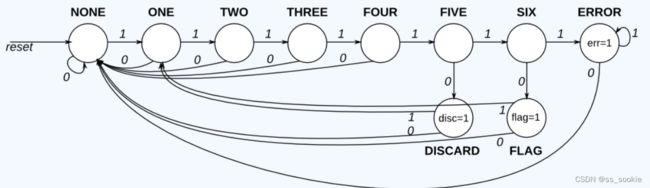
实现它就好啦!
21 Q8: design a Mealy FSM
1.代码编写
module top_module (
input clk,
input aresetn, // Asynchronous active-low reset
input x,
output z );
reg [1:0] state,next_state;
parameter [1:0] IDLE = 2'd0,S1=2'd1,S2 = 2'd2;
// state transfer
always@(*) begin
case(state)
IDLE: begin
next_state = (x)? S1:IDLE;
end
S1: begin
next_state = (x)? S1:S2;
end
S2: begin
next_state = (x)? S1:IDLE;
end
endcase
end
// flip-flop
always@(posedge clk,negedge aresetn) begin
if(~aresetn)
state <= IDLE;
else
state <= next_state;
end
// output
always@(*) begin
if(~aresetn)
z <= 1'b0;
else if(state == S2&&x==1'b1)
z <= 1'b1;
else
z <= 1'b0;
end
endmodule
2.提交结果
Success
3.题目分析
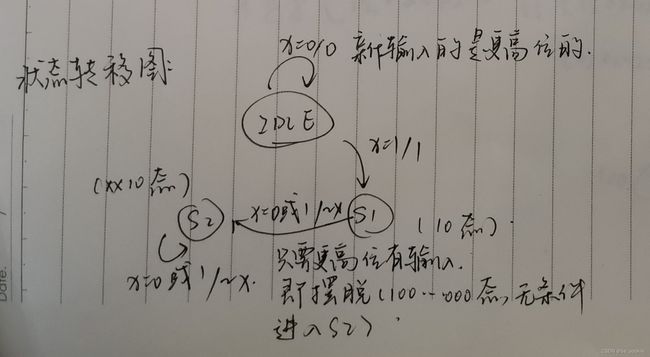
Implement a Mealy-type finite state machine that recognizes the sequence “101” on an input signal named x. Your FSM should have an output signal, z, that is asserted to logic-1 when the “101” sequence is detected. Your FSM should also have an active-low asynchronous reset. You may only have 3 states in your state machine. Your FSM should recognize overlapping sequences.
M o o r e 状态数:收数据状态 + 1 ( I D L E )(只要到达最后一个状态,无论再输入什么输出都是一定的,因为都成功接收了,所以输入仅决定 n e x t s t a t e 而不决定 o u t p u t ), {\color{blue}Moore 状态数:收数据状态+1(IDLE)(只要到达最后一个状态,无论再输入什么输出都是一定的,因为都成功接收了,所以输入仅决定next_state而不决定output),} Moore状态数:收数据状态+1(IDLE)(只要到达最后一个状态,无论再输入什么输出都是一定的,因为都成功接收了,所以输入仅决定nextstate而不决定output),
M e a l y 状态数:收数据状态(少最后一个状态,多一个 I D L E ,倒数第二个状态的 n e x t s t a t e 取决于输入,输出也取决于输入)。 {\color{blue}Mealy状态数:收数据状态(少最后一个状态,多一个IDLE,倒数第二个状态的next_state取决于输入,输出也取决于输入)。} Mealy状态数:收数据状态(少最后一个状态,多一个IDLE,倒数第二个状态的nextstate取决于输入,输出也取决于输入)。
状态转移图如下:

22 Q5a: Serial two’s complementer(Moore FSM)
1.代码编写
module top_module (
input clk,
input areset,
input x,
output z
);
reg [1:0] state,next_state;
parameter [1:0] IDLE = 2'd0,S1 = 2'd1,S2 = 2'd2;
// state transfer
always@(*) begin
case(state)
IDLE: begin
next_state = (x)? S1:IDLE;
end
S1: begin
next_state = S2;
end
S2: begin
next_state = S2;
end
endcase
end
// flip-flop
always@(posedge clk,posedge areset) begin
if(areset)
state <= IDLE;
else
state <= next_state;
end
always@(posedge clk, posedge areset) begin
if(areset)
z = 1'b0;
else begin
case(next_state)
IDLE: begin
z = 1'b0;
end
S1: begin
z = 1'b1;
end
S2: begin
z = ~x;
end
endcase
end
end
endmodule
2.提交结果
3.题目分析
You are to design a one-input one-output serial 2’s complementer Moore state machine. The input (x) is a series of bits (one per clock cycle) beginning with the least-significant bit of the number, and the output (Z) is the 2’s complement of the input. The machine will accept input numbers of arbitrary length. The circuit requires an asynchronous reset. The conversion begins when Reset is released and stops when Reset is asserted.
- IDLE: 输出都是0,此时输出(比特流的补码)也都是0。
- S1:刚刚输入了第一个1(还作为最高位),输入比特流为 100……000,此时的输出(比特流的补码)与输入一致
- S2: 输入了不止一个1或输入了一个1但以不在最高位,此时的输出(比特流的补码)遵循这样一个规律:“1”中处在最低位的那个保持,比其更高的bit位全部取反。
在断言 M o o r e 及 M e a l y 状态机的输出时, M o o r e 一般判断条件为 n e x t s t a t e , M e a l y 为 s t a t e 与 i n p u t ,二者都放在时序逻辑时, M e a l y 会比 M o o r e 慢一个 c l k c y c l e {\color{blue}在断言Moore及Mealy状态机的输出时,Moore一般判断条件为next_state,Mealy为state与input,二者都放在时序逻辑时,Mealy会比Moore慢一个clk cycle} 在断言Moore及Mealy状态机的输出时,Moore一般判断条件为nextstate,Mealy为state与input,二者都放在时序逻辑时,Mealy会比Moore慢一个clkcycle
23 Q5b: Serial two’s complementer(Mealy FSM)
1.代码编写
module top_module (
input clk,
input areset,
input x,
output z
);
reg [1:0] state,next_state;
parameter [1:0] A = 2'd01,B = 2'd10;
// state transfer
assign next_state[0] = ~x&&state[0];
assign next_state[1] = state[1] || ~state[1]&&x;
// flip-flop
always@(posedge clk,posedge areset) begin
if(areset)
state <= A;
else
state <= next_state;
end
// output
always@(*) begin // 组合逻辑赋值保证output变化与state变化之间不延迟
// if(areset)
// z = 1'b0;
if(state == A&&x || state == B&&~x)
z = 1'b1;
else
z = 1'b0;
end
endmodule
2.提交结果
3.题目分析
The following diagram is a Mealy machine implementation of the 2’s complementer. Implement using one-hot encoding.
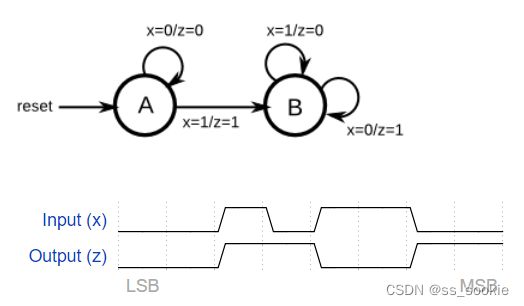
有一篇介绍Moore和Mealy状态机的文章,感觉不错
https://blog.csdn.net/weixin_43727437/article/details/104654195
24 Q3a FSM(Exams/2014 q3fsm)
1.代码编写
module top_module (
input clk,
input reset, // Synchronous reset
input s,
input w,
output z
);
reg breset;
reg [1:0] cnt;
reg [2:0] in;
reg [1:0] state,next_state;
parameter[1:0] A = 2'd0,B = 2'd1;
// state transfer
always@(*) begin
case(state)
A: begin
next_state = (s)? B:A;
end
B: begin
next_state = B;
end
default: next_state = A;
endcase
end
// flip-flop
always@(posedge clk) begin
if(reset)
state <= A;
else
state <= next_state;
end
// output
always@(posedge clk) begin
in <= (state == B)? {w,in[2:1]}:3'd0; // 这里next_state和state是一样的,只是多读一个最后的A时的in,但这个in不计入z。
cnt <= (state == B && cnt != 2'd2)? cnt+2'd1:2'd0;
breset <= reset;
end
assign z = (cnt == 2'd0&&~breset)? (in[2]&in[1]&~in[0])|(in[2]&~in[1]&in[0])|(~in[2]&in[1]&in[0]):1'b0;//in中有大于等于2个1,z才得1
endmodule
这题写了一天啊,可难坏我了,写这道题的时候用了类似前面几道题的datapass,一开始不能通过,本想学习其他作者的方法,设置一个cnt来记录B状态的cycle数,另一个w_cnt记录这3个cyc中w=1的状态数。
BUT!后来越发觉得我写的也有道理,不应该有错的,遂改代码改了大半天……
最后,没有加倒数第4行的breset <= reset;,倒数第2行条件里也没有~breset。
// output
always@(posedge clk) begin
in <= (state == B)? {w,in[2:1]}:3'd0; // 这里next_state和state是一样的,只是多读一个最后的A时的in,但这个in不计入z。
cnt <= (state == B && cnt != 2'd2)? cnt+2'd1:2'd0;
end
assign z = (cnt == 2'd0)? (in[2]&in[1]&~in[0])|(in[2]&~in[1]&in[0])|(~in[2]&in[1]&in[0]):1'b0;//in中有大于等于2个1,z才得1
仿真报错:

发现,这应该是在正常的B状态下,进行reset的问题,我确实在一开始忽视了。
后尝试了直接
assign z = (cnt == 2'd0&&reset)? (in[2]&in[1]&~in[0])|(in[2]&~in[1]&in[0])|(~in[2]&in[1]&in[0]):1'b0;
这显然不可取,这会使只要reset=1,便置z=0。而z应是在reset=1状态下的时钟上升沿被置位的。
而我已经用了组合逻辑进行输出,将其改为时序逻辑又引发了很多有关延迟的错误。
遂,直接让reset延迟一个周期,且在下一周期保持时钟上升沿时的reset取值(在flip-flop中由非阻塞赋值直接可以实现)之后用组合输出,便可得到正确结果。
2.提交结果
Success
3.题目分析
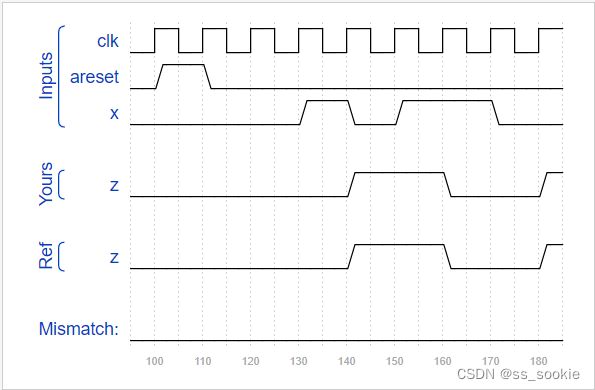
Consider a finite state machine with inputs s and w. Assume that the FSM begins in a reset state called A, as depicted below. The FSM remains in state A as long as s = 0, and it moves to state B when s = 1. Once in state B the FSM examines the value of the input w in the next three clock cycles. If w = 1 in exactly two of these clock cycles, then the FSM has to set an output z to 1 in the following clock cycle. Otherwise z has to be 0. The FSM continues checking w for the next three clock cycles, and so on. The timing diagram below illustrates the required values of z for different values of w.
Use as few states as possible. Note that the s input is used only in state A, so you need to consider just the w input.
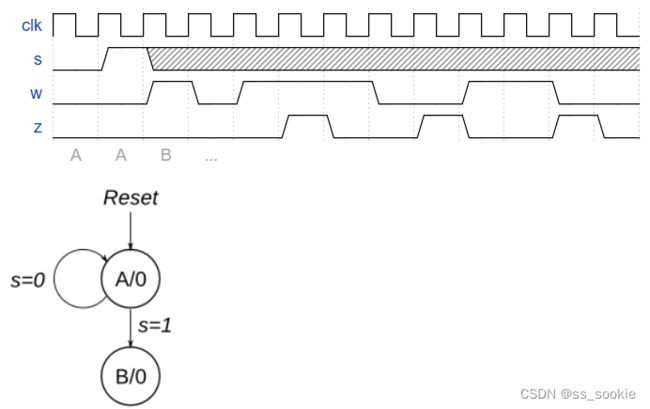
由我的代码进行分析:

cnt:state步入B的下一个状态cnt=1,每一个cnt=0,认为是3个cycle之后的那个cycle,刚好需要进行组合逻辑输出(不能再滞后了)。
in:由flip-flip,in的bit比w滞后一个cycle,刚好在cnt=0,in收集了三个需要的w,刚好在这时需进行组合逻辑判断(不能再滞后了)。
25 Q3b:FSM(Exams/2014 q3bfsm)
1.代码编写
module top_module (
input clk,
input reset, // Synchronous reset
input x,
output z
);
reg [2:0] state,next_state;
parameter [2:0] S1 = 3'b000,S2 = 3'b001,S3 = 3'b100,S4 = 3'b011,S5 = 3'b010;
// state transfer
always@(*) begin
case(state)
S1: begin
next_state = (x)? S2:S1;
end
S2: begin
next_state = (x)? S3:S2;
end
S3: begin
next_state = (x)? S3:S4;
end
S4: begin
next_state = (x)? S5:S2;
end
S5: begin
next_state = (x)? S2:S5;
end
endcase
end
// flip-flop
always@(posedge clk) begin
if(reset)
state <= S1;
else
state <= next_state;
end
// output;
assign z = (state == S3 || state == S4)? 1'b1:1'b0;
endmodule
2.提交结果
Success
3.题目分析
Given the state-assigned table shown below, implement the finite-state machine. Reset should reset the FSM to state 000.
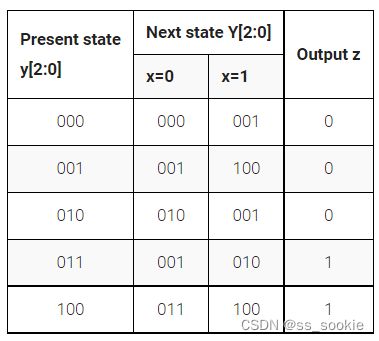
这道不怎么难
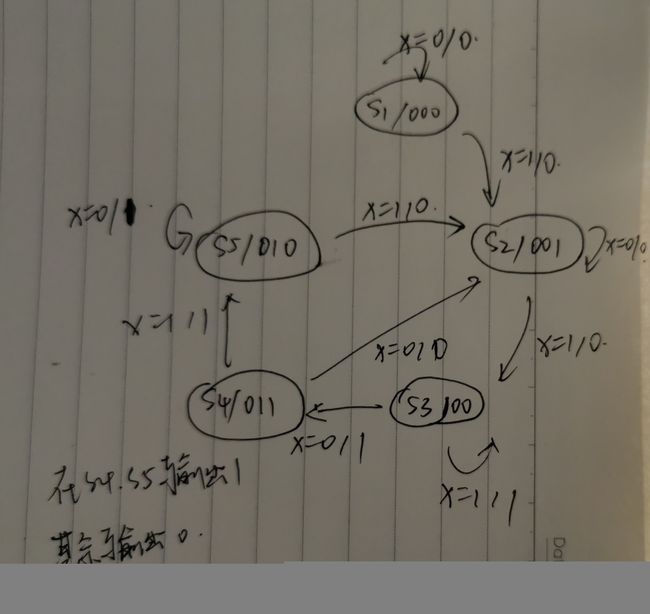
26 Q3c:FSM logic
1.代码编写
module top_module (
input clk,
input [2:0] y, // 是输入的state
input x,
output Y0,
output z
);
reg [2:0] next_state;
parameter [2:0] S1 = 3'b000,S2 = 3'b001,S3 = 3'b100,S4 = 3'b011,S5 = 3'b010;
// state transfer
always@(*) begin
case(y)
S1: begin
next_state = (x)? S2:S1;
end
S2: begin
next_state = (x)? S3:S2;
end
S3: begin
next_state = (x)? S3:S4;
end
S4: begin
next_state = (x)? S5:S2;
end
S5: begin
next_state = (x)? S2:S5;
end
default: next_state = S1;
endcase
end
// output;
assign z = (y == S3 || y == S4);
assign Y0 = next_state[0];
endmodule
2.提交结果
Success
3.题目分析
Given the state-assigned table shown below, implement the logic functions Y[0] and z.
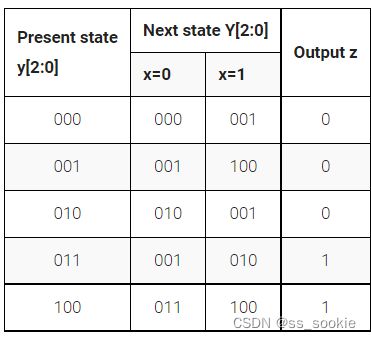
这道题不难,一开始错在了读题上。
- 这里是implement Y[0]和z,而不是整个FSM。
- 上图中标注了,“Next state Y[2:0]”,所以Y0是Next state的最低位,而不是state的最低位。
27 Q6b:FSM next state logic
1.代码编写
module top_module (
input [3:1] y,
input w,
output Y2);
reg [3:1] next_state;
parameter[3:1] A = 3'b000,B = 3'b001,C = 3'b010,D = 3'b011,E = 3'b100,F = 3'b101;
// Implement just the next-state logic for y[2].
// state transfer
always@(*) begin
case(y)
A: begin
next_state = (w)? A:B;
end
B: begin
next_state = (w)? D:C;
end
C: begin
next_state = (w)? D:E;
end
D: begin
next_state = (w)? A:F;
end
E: begin
next_state = (w)? D:E;
end
F: begin
next_state = (w)? D:C;
end
endcase
end
// output
assign Y2 = next_state[2];
endmodule
2.提交结果
Success
3.题目分析
Consider the state machine shown below, which has one input w and one output z.
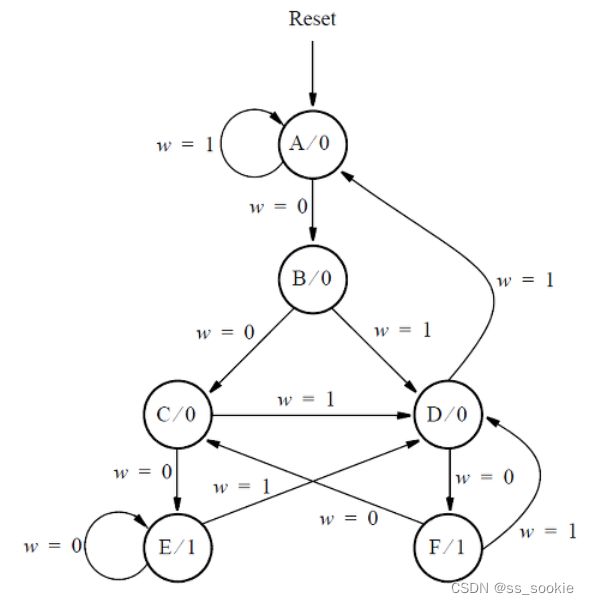
Assume that you wish to implement the FSM using three flip-flops and state codes y[3:1] = 000, 001, … , 101 for states A, B, … , F, respectively. Show a state-assigned table for this FSM. Derive a next-state expression for the flip-flop y[2].
Implement just the next-state logic for y[2]. (This is much more a FSM question than a Verilog coding question. Oh well.)
这题就状态转移图看着复杂一些。
做出状态转移矩阵如下:

另外注意,只需要综合Y[2](next_state of y[2])的输出逻辑,而非综合出一整个FSM。
28 Q6c:FSM one-hot next state logic
1.代码编写
module top_module (
input [6:1] y,
input w,
output Y2,
output Y4);
reg [6:1] next_state;
parameter [6:1] A = 6'b000001,B = 6'b000010,C = 6'b000100,D = 6'b001000,E = 6'b010000,F = 6'b100000;
always@(*) begin
next_state[1] = (y[1]||y[4])&&w;
next_state[2] = y[1]&&~w;
next_state[3] = (y[2]||y[6])&&~w;
next_state[4] = (y[2]||y[3]||y[5]||y[6])&&w;
next_state[5] = (y[3]||y[5])&&~w;
next_state[6] = y[4]&&~w;
end
assign Y2 = next_state[2];
assign Y4 = next_state[4];
endmodule
2.提交结果
Success
3.题目分析
Consider the state machine shown below, which has one input w and one output z.
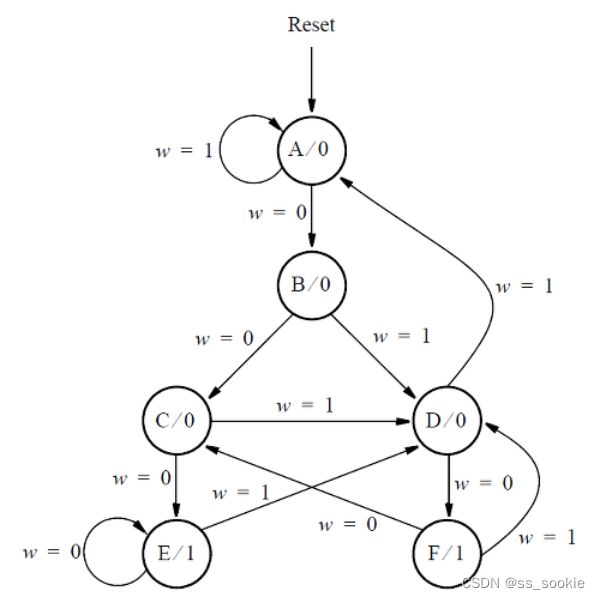
For this part, assume that a one-hot code is used with the state assignment 'y[6:1] = 000001, 000010, 000100, 001000, 010000, 100000 for states A, B,…, F, respectively.
Write a logic expression for the next-state signals Y2 and Y4. (Derive the logic equations by inspection assuming a one-hot encoding. The testbench will test with non-one hot inputs to make sure you’re not trying to do something more complicated).
和上一道题差不多,用到了独热码的组合逻辑。
对上一题的状态转移图做出改进:

29 Q6:FSM (Exams/m2014 q6)
1.代码编写
用独热码:
module top_module (
input clk,
input reset, // synchronous reset
input w,
output z);
reg [6:1] y,next_state; // y for current state
parameter [6:1] A = 6'b000001,B = 6'b000010,C = 6'b000100,D = 6'b001000,E = 6'b010000,F = 6'b100000;
// state transfer (one-hot bit)
always@(*) begin
next_state[1] = (y[1]||y[4])&&w;
next_state[2] = y[1]&&~w;
next_state[3] = (y[2]||y[6])&&~w;
next_state[4] = (y[2]||y[3]||y[5]||y[6])&&w;
next_state[5] = (y[3]||y[5])&&~w;
next_state[6] = y[4]&&~w;
end
// flip-flop
always@(posedge clk) begin
if(reset)
y <= A;
else
y <= next_state;
end
// output
assign z = y[5]||y[6];
endmodule
用非独热码:
module top_module (
input clk,
input reset, // synchronous reset
input w,
output z);
reg [3:1] state,next_state;
parameter[3:1] A = 3'b000,B = 3'b001,C = 3'b010,D = 3'b011,E = 3'b100,F = 3'b101;
// Implement just the next-state logic for y[2].
// state transfer
always@(*) begin
case(state)
A: begin
next_state = (w)? A:B;
end
B: begin
next_state = (w)? D:C;
end
C: begin
next_state = (w)? D:E;
end
D: begin
next_state = (w)? A:F;
end
E: begin
next_state = (w)? D:E;
end
F: begin
next_state = (w)? D:C;
end
endcase
end
// flip-flop
always@(posedge clk) begin
if(reset)
state <= A;
else
state <= next_state;
end
// output
assign z = (state == E) || (state == F);
endmodule
2.提交结果
Success
3.题目分析
Consider the state machine shown below, which has one input w and one output z.
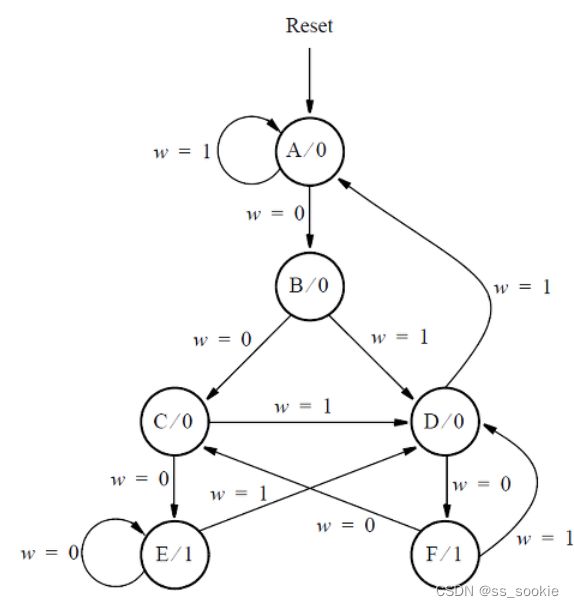
Implement the state machine. (This part wasn’t on the midterm, but coding up FSMs is good practice).
综合一整个FSM,而不是其中的一部分。
对前两道题稍加改动即可。
30 Q2a:FSM (Exams/2012 q2fsm)
1.代码编写
module top_module (
input clk,
input reset, // Synchronous active-high reset
input w,
output z
);
reg [2:0] state,next_state;
parameter [2:0] A = 3'd0,B = 3'd1,C = 3'd2,D = 3'd3,E = 3'd4,F = 3'd5;
// state transfer
always@(*) begin
case(state)
A: begin
next_state = (w)? B:A;
end
B: begin
next_state = (w)? C:D;
end
C: begin
next_state = (w)? E:D;
end
D: begin
next_state = (w)? F:A;
end
E: begin
next_state = (w)? E:D;
end
F: begin
next_state = (w)? C:D;
end
endcase
end
// flip-flop
always@(posedge clk) begin
if(reset)
state <= A;
else
state <= next_state;
end
// output
assign z = (state == E) || (state == F);
endmodule
2.提交结果
Success
3.题目分析
Consider the state diagram shown below.
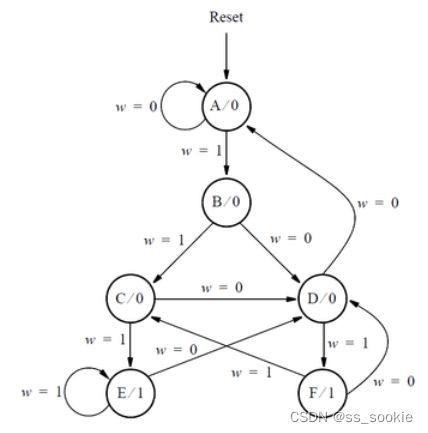
Write complete Verilog code that represents this FSM. Use separate always blocks for the state table and the state flip-flops, as done in lectures. Describe the FSM output, which is called z, using either continuous assignment statement(s) or an always block (at your discretion). Assign any state codes that you wish to use.
新的状态转移图,按照图进行代码实现即可。
31 One-hot FSM equations (Exams/2012 q2b)
1.代码编写
module top_module (
input [5:0] y,
input w,
output Y1,
output Y3
);
// Write a logic expression for the signal Y1, which is the input of state flip-flop y[1].
// Write a logic expression for the signal Y3, which is the input of state flip-flop y[3].
reg [5:0] next_state;
parameter [5:0] A = 6'b000001,B = 6'b000010,C = 6'b000100,D = 6'b001000,E = 6'b010000,F = 6'b100000;
// state transfer
always@(*) begin
next_state[0] = (y[0]||y[3])&&~w;
next_state[1] = y[0]&&w;
next_state[2] = (y[1]||y[5])&&w;
next_state[3] = (y[1]||y[2]||y[4]||y[5])&&~w;
next_state[4] = (y[2]||y[4])&&w;
next_state[5] = y[3]&&w;
end
assign Y1 = next_state[1];
assign Y3 = next_state[3];
endmodule
2.提交结果
Success
3.题目分析
The state diagram for this question is shown again below.

Assume that a one-hot code is used with the state assignment y[5:0] = 000001(A), 000010(B), 000100©, 001000(D), 010000(E), 100000(F)
Write a logic expression for the signal Y1, which is the input of state flip-flop y[1].
Write a logic expression for the signal Y3, which is the input of state flip-flop y[3].
(Derive the logic equations by inspection assuming a one-hot encoding. The testbench will test with non-one hot inputs to make sure you’re not trying to do something more complicated).
32 Q2a:FSM (Exams/2013 q2afsm)
1.代码编写
module top_module (
input clk,
input resetn, // active-low synchronous reset
input [3:1] r, // request
output [3:1] g // grant
);
reg [1:0] state,next_state;
parameter [1:0] A = 2'd0,B = 2'd1,C = 2'd2,D = 2'd3;
// state transfer
always@(*) begin
case(state)
A: begin
if(r[1])
next_state = B;
else if(r[2])
next_state = C;
else if(r[3])
next_state = D;
else
next_state = A;
end
B: begin
if(r[1])
next_state = B;
else
next_state = A;
end
C: begin
if(r[2])
next_state = C;
else
next_state = A;
end
D: begin
if(r[3])
next_state = D;
else
next_state = A;
end
endcase
end
// flip-flop
always@(posedge clk) begin
if(~resetn)
state <= A;
else
state <= next_state;
end
// output
assign g = {(state == D),(state == C),(state==B)};
endmodule
2.提交结果
Success
3.题目分析
Consider the FSM described by the state diagram shown below:

This FSM acts as an arbiter circuit, which controls access to some type of resource by three requesting devices. Each device makes its request for the resource by setting a signal r[i] = 1, where r[i] is either r[1], r[2], or r[3]. Each r[i] is an input signal to the FSM, and represents one of the three devices. The FSM stays in state A as long as there are no requests. When one or more request occurs, then the FSM decides which device receives a grant to use the resource and changes to a state that sets that device’s g[i] signal to 1. Each g[i] is an output from the FSM. There is a priority system, in that device 1 has a higher priority than device 2, and device 3 has the lowest priority. Hence, for example, device 3 will only receive a grant if it is the only device making a request when the FSM is in state A. Once a device, i, is given a grant by the FSM, that device continues to receive the grant as long as its request, r[i] = 1.
Write complete Verilog code that represents this FSM. Use separate always blocks for the state table and the state flip-flops, as done in lectures. Describe the FSM outputs, g[i], using either continuous assignment statement(s) or an always block (at your discretion). Assign any state codes that you wish to use.
这像是一个资源分配器,其中设备1的请求(r1,亦是r[1]具有最高优先级,2,3优先级降低)。
当决定给某个设备分配资源时,置g[i]=1,i为相应设备号。
以上功能均能由提供的状态转移(state-assigned graph)图满足。
33 Q2b:Another FSM (Exams/2013 q2bfsm)
1.代码编写
module top_module (
input clk,
input resetn, // active-low synchronous reset
input x,
input y,
output f,
output g
);
reg [3:0] state,next_state;
parameter [3:0] A = 4'd0,IDLE = 4'd1,S1 = 4'd2,S2 = 4'd3,S3 = 4'd4,R1 = 4'd5,R2 = 4'd6,R3 = 4'd7,R4 = 4'd8,IDLE2 = 4'd9;
// state transfer
always@(*) begin
case(state)
A: begin
next_state = IDLE2; // 修改1,延迟1个cycle进行x序列检查
end
IDLE2: begin
next_state = IDLE;
end
IDLE: begin
next_state = (x)? S1:IDLE;
end
S1: begin
next_state = (x)? S1:S2;
end
S2: begin
next_state = (x)? S3:IDLE;
end
S3: begin
next_state = (y)? R1:R2;
end
R1: begin
next_state = R3;
end
R2: begin
next_state = (y)? R3:R4;
end
R3: begin
next_state = R3;
end
R4: begin
next_state = R4;
end
default: next_state = A;
endcase
end
// flip-flopA
always@(posedge clk) begin
if(!resetn)
state <= A;
else
state <= next_state;
end
// output
always@(posedge clk) begin
if(!resetn) begin
f <= 1'b0;
g <= 1'b0;
end
else if(state == A && resetn) // Mealy!!
f <= 1'b1;
else if(next_state == S3 || next_state == R1 || next_state == R2 || next_state == R3)
g <= 1'b1;
else begin
f <= 1'b0;
g <= 1'b0;
end
end
endmodule
2.提交结果
Success
3.题目分析
Consider a finite state machine that is used to control some type of motor. The FSM has inputs x and y, which come from the motor, and produces outputs f and g, which control the motor. There is also a clock input called clk and a reset input called resetn.
The FSM has to work as follows. As long as the reset input is asserted, the FSM stays in a beginning state, called state A. When the reset signal is de-asserted, then after the next clock edge the FSM has to set the output f to 1 for one clock cycle. Then, the FSM has to monitor the x input. When x has produced the values 1, 0, 1 in three successive clock cycles, then g should be set to 1 on the following clock cycle. While maintaining g = 1 the FSM has to monitor the y input. If y has the value 1 within at most two clock cycles, then the FSM should maintain g = 1 permanently (that is, until reset). But if y does not become 1 within two clock cycles, then the FSM should set g = 0 permanently (until reset).
(The original exam question asked for a state diagram only. But here, implement the FSM.)
第一次提交(Incorrect):
做出 state transtion diagram:

错误波形如下:
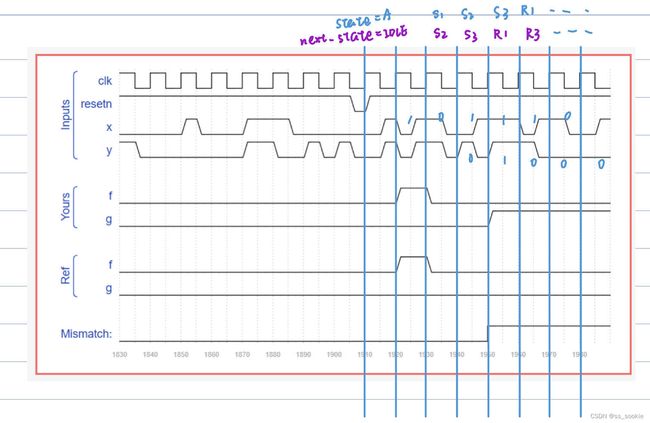
这于我的逻辑是自洽的,但从波形可以猜测:这是一个中途置位后,x 立即出现‘101’序列时的判断问题,结合题干中加粗的Then,猜测应该是令 f 输出一个完整时钟周期的 1 之后,再监控 x 序列。
只需要在 state = A 和 state = IDLE (监测resetn =0 -> 1的下一个x输入),之间多打一拍时钟即可。添加状态IDLE2。
新的 state transiton diagram 如下:

这样输出就正确啦!
我真傻,真的,一开始想要把几种不同颜色的部分设置为不同的FSM,前一个FSM会输出后一个FSM的使能信号,另外还想用cnt来记位,这可太麻烦啦!