HashMap源码解析【java进阶笔记二】

目录

知识储备

个人理解

源码解析：从构造函数入手

1> 创建table数组

2> 向table数组中赋值

 1） 没有发⽣哈希冲突

 2） 发生了哈希冲突

3> 如超过阈值，则进行扩容

---

知识储备

① HashMap 1.8前：数组+链表

                    ​  1.8后：数组+链表+红黑树

② 红⿊树 是⼀种⾃平衡的⼆叉树，它可以避免⼆分搜索树在极端的情况下蜕化成链表的情况。

​         ● 条件⼀：每个节点要么是红⾊，要么是⿊⾊。

​         ● 条件⼆：根节点⼀定是⿊⾊的。

​         ● 条件三：每个叶⼦节点⼀定是⿊⾊。

​         ● 条件四：如果⼀个节点是红⾊，那么它的左右⼦节点⼀定都是⿊⾊的。

​         ● 条件五：从任意⼀个节点到叶⼦节点，所经过的⿊⾊节点的数量⼀样多。

③ 2-3树 是⼀种绝对平衡的多叉树，在这棵树中，任意⼀个节点，它的左右⼦树的⾼度是相同的。

​         2-3树分为两种节点，分别为：2-节点和3-节点。其中，2-节点表示节点中保存⼀个元素，3-节点则表示节点中保存两个元素。

个人理解

        我一直很纠结上面说的 数组+链表+红黑树 的数据结构。所以花了点时间来理解了一下，不知道是否正确。我的理解是：HashMap 的存储结构本质上就是个数组 tab，只是数组里存的元素是节点node。这些节点根据长度来维护为单向链表或者红黑树（红黑树中的节点还同时维护一个双向链表）。

源码解析：从构造函数入手

// 1、构造函数
public HashMap() {
    this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

// 【变量源码】
// 负载因子：用于判定扩容
static final float DEFAULT_LOAD_FACTOR = 0.75f;

下面是整个框架的流程图，下面会具体分析，图放在这里就是为了有个大概印象

// 2、对 hashMap 对象进行操作
hashMap.put(0, "a0");
​
// 2.1 put 方法插入键值  返回插入的值
    public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }
​
// 2.2 进入 putVal() 函数，首先解析一下入参
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {}
/**
  *【参数解释】
  * @param hash         key 的哈希值
  * @param key          key 值
  * @param value        value 值
  * @param onlyIfAbsent 如果是 true ,则不改变已存在的 value 值，默认false：同 key 覆盖原值
  * @param evict        驱逐，赶出，逐出 if false, the table is in creation mode.
  *                                 实际上函数体为空，即什么都没做，默认为true
  *
  * @return previous value, or null if none
  */
​
    // hash() 函数用于计数 key 的哈希值【扰动函数】
    static final int hash(Object key) {
        int h;
        /**
         * 按位异或运算（^）：两个数转为二进制，然后从高位开始比较，如果相同则为0，不相同则为1。
         *
         * 扰动函数————(h = key.hashCode()) ^ (h >>> 16) 表示：
         *      将key的哈希code一分为二。其中：
         *      【高半区16位】数据不变。
         *      【低半区16位】数据与高半区16位数据进行异或操作，以此来加大低位的随机性。
         * 注意：如果key的哈希code小于等于16位，那么是没有任何影响的。
         * 只有大于16位，才会触发扰动函数的执行效果。
         * */
        // egx: 110100100110^000000000000=110100100110，由于k1的hashCode都是在低16位，
        //                                                           所以原样返回3366
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }

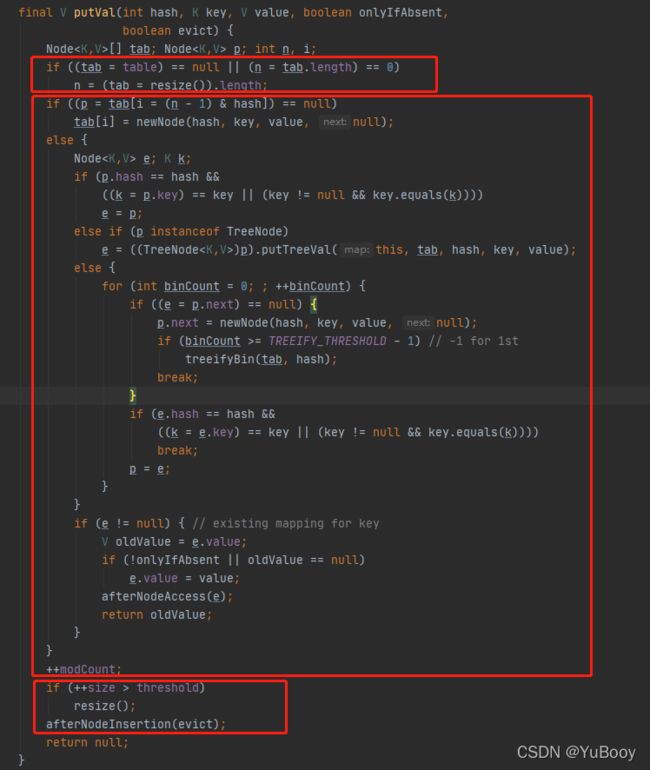
putVal 分成三部分内容：

1> 创建table数组

2> 向table数组中赋值，这⾥⾯分为哈希不冲突和哈希冲突两种情况。

3> 如果超过阈值，则进⾏扩容操作。

 

1> 创建table数组

// 3.1 第一次进入 resize() 创建一个 node 数组
/** 如果是空的table，那么默认初始化一个长度为16的Node数组*/
        if ((tab = table) == null || (n = tab.length) == 0) {
            // eg1: resize返回(Node[]) new Node[16]，
            // 所以：tab=(Node[]) new Node[16]， n=16
            n = (tab = resize()).length;
        }
// 【变量源码】
// 默认 table 数组为空
transient Node[] table;

resize() 函数是进行扩容的函数，但第一次调用则是进行新建。新建一个 table 数组仅用到下面框住的代码。

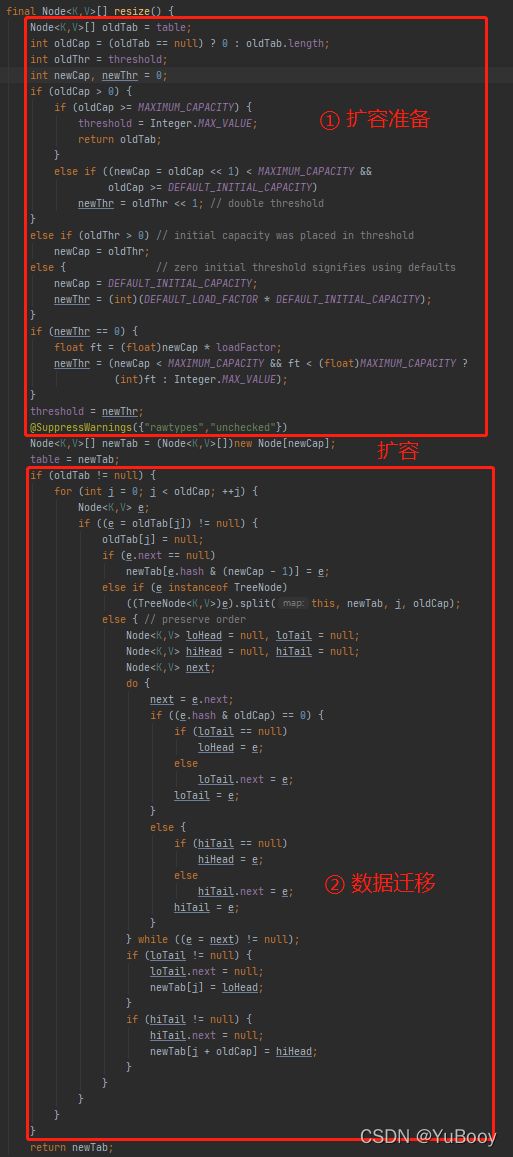
resize() 扩容函数分为 两部分：

① 计数新的长度；计数新的阈值；根据新的长度创建新的 table 数组；

② 数据迁移到新的 table 数组 （老 table 数组非空的话）。

// 【全局变量】
transient Node[] table;  //当前所使⽤的table数组
int threshold;                 //当前所使⽤的table数组的阈值。
final float loadFactor;        //当前所使⽤的table数组的加载因⼦
this.loadFactor = DEFAULT_LOAD_FACTOR; // 在构造函数完成了赋值
​
// 【局部变量】
Node[] oldTab = table;   //oldTab： 表示旧的table数组
int oldThr = threshold;        //oldThr： 表示旧table数组的阈值
int oldCap = (oldTab == null) ? 0 : oldTab.length;//oldCap： 表示旧table数组的容量/⻓度
Node[] newTab = (Node[]) new Node[newCap];//newTab： 表示新的table数组
int newThr = 0;                //表示新table数组的阈值
int newCap = 0;                //表示新table数组的容量/⻓度

下面对第一部分：扩容准备进行具体分析：

Node[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;

● 由于是第⼀次调⽤put⽅法，所以是第一次进入 resize() 函数，所以 table 数组还没有被初始化，所以它默认是 null 的，所以 oldTab 也等于 null，oldCap就等于0了。

● threshold 的默认值是0，所以oldThr也等于0。

if (oldCap > 0) {
    if (oldCap >= MAXIMUM_CAPACITY) {
        threshold = Integer.MAX_VALUE;
        return oldTab;
    }
    else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY)
        newThr = oldThr << 1; 
}
else if (oldThr > 0) 
    newCap = oldThr;
else {             
    newCap = DEFAULT_INITIAL_CAPACITY;
    newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}

判断1：如果旧的table数组⻓度⼤于0（即：oldCap > 0）说明当前 table 数组有数据

        判断1.1：如果旧 table 数组⻓度⼤于等于最⼤容量（MAXIMUM_CAPACITY）

​                 则阈值 threshold 被赋值为 Integer 的最⼤值，返回旧的 table 数组。

// 【变量源码】
// MAXIMUM_CAPACITY 表示的⼆进制为 1000 0000 0000 0000 0000 0000 0000 0000
static final int MAXIMUM_CAPACITY = 1 << 30;
​
// MAX_VALUE 为2^31-1  1后面有30个1 
// 表示的⼆进制为 01111111 11111111 11111111 11111111 = 2147483647
@Native public static final int   MAX_VALUE = 0x7fffffff;

        判断1.2： newCap = oldCap << 1 表示将 oldCap 左移1位，也就是按照 oldCap*2 来扩容

​         条件1：新的 table 数组容量（newCap）⼩于 MAXIMUM_CAPACITY

​         条件2：旧的 table 数组容量（oldCap）⼤于等于 DEFAULT_INITIAL_CAPACITY（默认值为：16）

​                 都满足则 threshold 阈值也左移1位，阈值提示一倍。

// 【变量源码】
// 默认初始长度为 16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; 

---

else if (oldThr > 0) 
    newCap = oldThr;

判断2：如果旧的 table 数组阈值⼤于0（即：oldThr > 0）

        判断1 为假（即：oldCap <= 0） table 数组容量小于等于0，但判断2为真（即：oldThr > 0）旧 table 数组阈值大于0。说明 table 数组太⼤了，以⾄于⻓度越界了，出现了从整数变为了负数的情况。如果这种情况发⽣了，那么就将旧的 table 数组的阈值作为新 table 数组的容量进⾏赋值，相当于适度的进⾏⻓度修复。

---

else {             
    newCap = DEFAULT_INITIAL_CAPACITY;
    newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}

判断3：如果上⾯条件都不满⾜，就执⾏判断3

通过上⾯的判断1和判断2，可以知道首次进入 resize() 函数时，对 table 数组进行初始化，就会进⼊到判断3的代码。做两件事：

1> 将新的 table 数组⻓度赋值为 DEFAULT_INITIAL_CAPACITY。（这个默认值为16）

2> 将新的 table 数组的阈值赋值为 ：

        DEFAULT_INITIAL_CAPACITY * DEFAULT_INITIAL_CAPACITY = 16 * 0.75=12。

DEFAULT_INITIAL_CAPACITY 负载因子默认值为0.75f。

---

// 判断2
else if (oldThr > 0) 
    newCap = oldThr;
​
// 判断4
if (newThr == 0) {
    float ft = (float) newCap * loadFactor;
    newThr = (newCap < MAXIMUM_CAPACITY && ft < (float) MAXIMUM_CAPACITY ? 
              (int) ft : Integer.MAX_VALUE);
}

上面的判断还剩下一部分：判断4： （即 newThr == 0）这块代码

这部分主要是为上⾯【判断2：旧的 table 数组阈值⼤于0（即：oldThr > 0）】服务的。因为进⼊到判断2，说明旧的 table 数组太⼤导致越界变为负数。判断2⾥只是对 newCap 赋值了，并没有赋值newThr，所以进入判断4 对 newThr 进行赋值。

① 首先通过 ft = 0.75f * newCap，

② 然后判断新的阈值（ft）是否⼩于最⼤容量（MAXIMUM_CAPACITY），且新的容量（newCap）是否小于最⼤容量（MAXIMUM_CAPACITY）。是的话则作为新的阈值了。否则，那么就默认赋值为 Integer 的最⼤值 （Integer.MAX_VALUE）

---

上面的判断确定了新的 table 数组的容量 （newCap）和阈值（newThr），为了下⾯创建新的 table 数组作准备。

threshold = newThr;
Node[] newTab = (Node[])new Node[newCap];
table = newTab;

首次对 HashMap 进行 put 操作，调用是的 resize() 函数进行的 table 数组创建，用到的代码是上图框住的部分。下面 if( oldTab != null ) 部分代码是进行数组扩容后数据迁移操作的，第一次初始化操作并不涉及，就留到下面再次进 resize() 函数扩容的时候再分析。

2> 向table数组中赋值

这一部分又可分成哈希冲突和哈希不冲突两部分，而哈希冲突又可分成三种情况。所以这部分代码比较多，也比较绕。这部分代码才是 HashMap 的核心。下图简单对整个赋值架构有个映像。

 

再看看整个 putVal

 1） 没有发⽣哈希冲突

if ((p = tab[i = (n - 1) & hash]) == null)
    tab[i] = newNode(hash, key, value, null);

通过 (n - 1) & hash 来寻址，找到待插⼊的位置 i，tab 就是 table 数组1>中赋值，如果发现 tab[i] == null，也就是待插⼊的位置是空的，直接插⼊就可以了。

如果 tab[i] 为空，说明哈希不冲突 ，通过 newNode ⽅法构建 Node 节点，最后放到刚刚寻址的 tab[i] 上⾯。

Node newNode(int hash, K key, V value, Node next) {
    return new Node<>(hash, key, value, next);
}

 2） 发生了哈希冲突

 

2.1） 冲突的节点key值相同

p = tab[i = (n - 1) & hash]
Node e; K k;
​
if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
    e = p;

把旧的 Node 节点取出来赋值给新节点 e，然后在最后执行以下代码，进行覆盖（onlyIfAbsent 在 调用 put() 函数时默认赋值了 false）。如果我们要覆盖旧值，则 onlyIfAbsent=false，如果不覆盖，则 onlyIfAbsent=true

if (e != null) { 
    V oldValue = e.value;
    if (!onlyIfAbsent || oldValue == null)
        e.value = value;
    afterNodeAccess(e);
    return oldValue;
}

2.2）红黑树结构处理

else if (p instanceof TreeNode)
    e = ((TreeNode)p).putTreeVal(this, tab, hash, key, value);

p 为寻址得到的节点，此节点为 TreeNode 节点的话，则进行红黑树的插入处理。

下图为 TreeNode 的结构关系。

 

● 从源码中可以看出来，TreeNode包含两部分内容：

1> 树结构（⽗节点：parent，左⼦节点：left，右⼦节点：right）

2> 链表结构（前指针：prev，后指针：next）

next 指针是在 TreeNode 祖⽗类 HashMap.Node ⾥⾯定义的。

下面具体分析红黑树结构处理的 putTreeVal() 函数

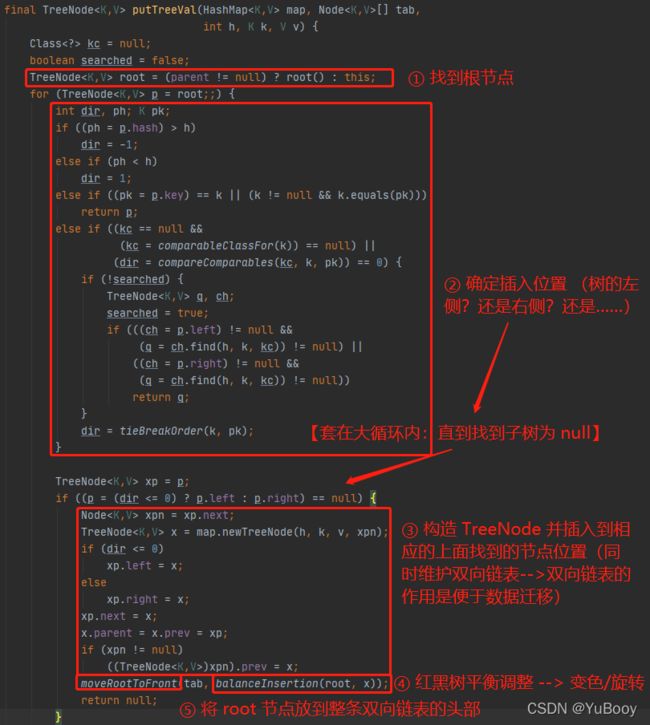
 putTreeVal ⽅法分为5部分，分别是：

● 1> 找到根节点

● 2> 确定插⼊位置

● 3> 构造 TreeNode 并插⼊到相应的⼦节点位置

● 4> 红⿊树平衡调整

● 5> moveRootToFront

2.2.1）找到根节点

TreeNode root = (parent != null) ? root() : this;

为了插入需要先找到插入的位置，在树结构里查找位置就需要先找到根节点。通过当前节点的 parent 节点来迭代寻找根节点。那这个当前节点是谁呢？这需要往回看，看是谁调用的 putTreeVal方法。如下图，是 p 节点调用的putTreeVal 方法。而 p 节点则是通过 hash 寻址的节点。

 如果 p 的⽗节点等于 null，则说明节点 p 就是 root 根节点，如果不等于null，就需要调⽤ root() ⽅法来进⾏迭代查找了。顺着 p 节点的⽗类往上查找⽗类，直到找到⼀个节点它没有⽗节点，则这个节点就是 root 根节点。

final TreeNode root() {
    for (TreeNode r = this, p;;) {
        if ((p = r.parent) == null)
            return r;
        r = p;
    }
}

2.2.2） 确定插⼊位置

for (TreeNode p = root; ; ) {
    int dir, ph;
    K pk;
    if ((ph = p.hash) > h) {
        dir = -1;
    } else if (ph < h) {
        dir = 1;
    } else if ((pk = p.key) == k || (k != null && k.equals(pk))) {
        return p;
    } else if ((kc == null && (kc = comparableClassFor(k)) == null) ||
                        (dir = compareComparables(kc, k, pk)) == 0) {
        if (!searched) {
            TreeNode q, ch;
            searched = true;
            if (((ch = p.left) != null &&
                    (q = ch.find(h, k, kc)) != null) ||
                      ((ch = p.right) != null &&
                      (q = ch.find(h, k, kc)) != null)) {
                            return q;
            }
        }
        dir = tieBreakOrder(k, pk);
    }
    TreeNode xp = p;
    if ((p = (dir <= 0) ? p.left : p.right) == null) {
        ……
    }
}

这部分代码就是对⽐ p 节点的 hash 值与待插⼊元素的 hash值：

① 如果 p 节点 hash 值⼤，则说明待插⼊的元素在 p 节点的左侧；

② 如果 p 节点 hash 值⼩，则说明待插⼊的元素在 p 节点的右侧；

③ 如果 p 节点的 key 值就是我们待插⼊的 key 值，返回 p 节点给上层调用。

可以看到最外层的 for 循环是⽆限循环的，就是说会慢慢的向下寻找，直到找到⼀个节点，它的左子节点或者右子节点为 null ，那么就插⼊了。这个过程和搜索⼆叉树中某个值的过程是⼀样的。

2.2.3）构造 TreeNode 并插⼊到相应的⼦节点位置

TreeNode xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
    Node xpn = xp.next;
    TreeNode x = map.newTreeNode(h, k, v, xpn);
    if (dir <= 0)
        xp.left = x;
    else
        xp.right = x;
    xp.next = x;
    x.parent = x.prev = xp;
    if (xpn != null)
        ((TreeNode)xpn).prev = x;
    ……
}

这部分需要完成两件事：① 树结构插入数据；② 链表结构插入并维护双向链表。

有几个局部变量需要了解：（树与链表结构并存，但操作的时候分开操作）

● x 表示待插⼊的树节点。

● xp 表示 x 节点的 parent 节点。

● xpn 表示 xp 的 next 节点，即后置节点。

首先在插入之前要新建一个 TreeNode 节点

TreeNode x = map.newTreeNode(h, k, v, xpn);

然后 ① 完成树结构插入数据

插入到左子树还是右子树是通过上面第二部计算的 dir 决定的：

dir = -1：表示待插⼊节点在 p 节点的左侧

dir = 1：表示待插⼊的节点在 p 节点的右侧

如果 p.left 等于 null，说明 p 是没有左⼦节点的，那么我们就可以执⾏插⼊操作 xp.left = x

之后再 ② 链表结构插入数据并维护双向链表

将新节点 x 插入到原来链表的 xp 和 xpn 之间

TreeNode x = map.newTreeNode(h, k, v, xpn);// 构造函数实例对象，参数 xpn 是指向 x.next 的指针
​
xp.next = x;                // xp.next 指向 x 的指针
x.parent = x.prev = xp;     // x.parent 指向 xp 维护树结构；x.prev 指向 xp 维护链表结构
if (xpn != null)
    ((TreeNode)xpn).prev = x; // xpn.prev 指向 x 的指针
​

// 构造函数实例对象，参数 xpn 是指向 x.next 的
Node(int hash, K key, V value, Node next) {
    this.hash = hash;
    this.key = key;
    this.value = value;
    this.next = next;
}

2.2.4）红⿊树平衡调整

上面完成新节点的插入之后，需要进行红黑树的平衡调整 balanceInsertion(root, x)

【红黑树的五大基本特性】

① 每个节点或者为红色，或者为黑色

② 根节点的颜色一定是黑色

③ 每一个叶子节点（最后的根节点）一定是黑色的

④ 如果一个节点是红色的，那么它的孩子节点都是黑色的

⑤ 从任意一个节点到叶子节点，经过的黑色节点的数量一样多

红黑树的平衡调整，本质上就是根据位置进行变色和左右旋转。下图是程序分析：

 主要是两部分：① 变色；② 旋转

① 变色：

 ② 旋转：

 具体的左旋操作函数 rotateLeft() 和右旋操作函数 rotateRight() 这里就不分析了，本质上就是根据位置改变链接指针指向的位置。具体的分析在最后的参考链接里有详细的图解分析，可以去看看。

 

2.2.5）moveRootToFront

红⿊树的平衡操作后，需要执⾏ moveRootToFront ⽅法，将 root 节点放到整条双向链表的头部，并插⼊到table数组中。这是红黑树结构处理插入数据的最后一步。

注意：这里的双向链表 ，和平常说的 jdk 1.8 后 HashMap 结构为：链表 + 红⿊树 中的链表不是⼀个概念。此双向链表是红黑树上的节点维护的双向链表，作用是便于数据迁移。而 HashMap 结构的链表为单向链表，那个链表是在数据量较小的时候，未形成树结构时的存储结构（下面哈希冲突第三种情况会讲到）。

 

2.3）向单向链表中插入元素

上面的 2.2 部分以树结构插入数据，是在长度足够转换成红黑树结构之后的操作。但刚刚新建一个 HashMap对象，插入数据长度不足的时候，是以单向链表的方式存储数据。

 

// 【变量源码】
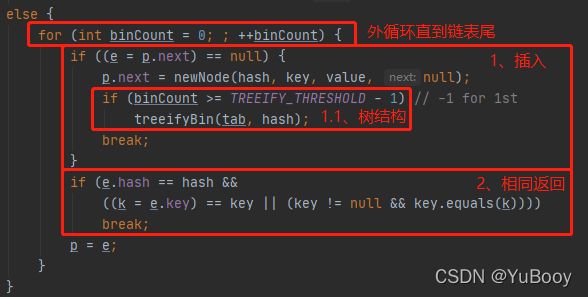
static final int TREEIFY_THRESHOLD = 8;

● 外面的 for 循环一直找到能插入数据的链表尾，然后分成两种情况：① 插入；② 比较hash 和 key 值，都相同则直接返回，后面根据 onlyIfAbsent 来选择是否覆盖旧的 value 值。

● 新建节点插入后，会根据阈值进行判断，判断是否需要转变成红黑树（ treeifyBin() 函数）。注意：binCount 是从0开始的，但对应的是链表中的第 2个 元素，⽽TREEIFY_THRESHOLD 默认值为 8，则只要 binCount >= 8-1，则尝试转变红⿊树（是否转变，还要看 treeifyBin ⾥⾯的逻辑）。 当 binCount >=7 的时候，其实链表中的元素已经超过了8个。

treeifyBin() 函数：

// 【变量源码】
static final int MIN_TREEIFY_CAPACITY = 64;

● treeifyBin 可以分为两部分：

1> table 数组⻓度⼩于64，只扩容 table 数组，不转换为红⿊树

2> table 数组⻓度大于64，则转换为红⿊树

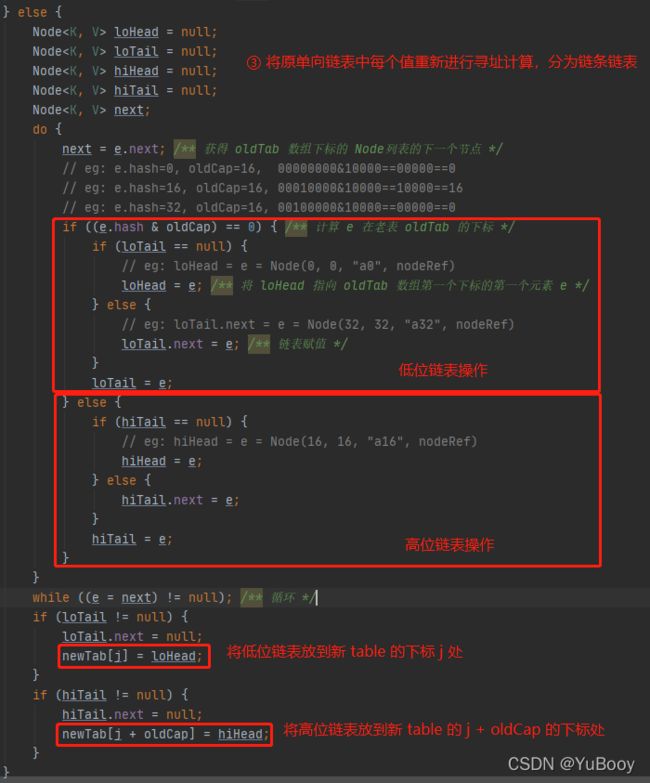
扩容 resize() 函数：

 第一部分扩容准备已经在上面 2> 向 table 数组中赋值讲过，下面就分析第二部分数据迁移部分。这一部分又可以分成三种情况：

 为方便理解上图说的单向链表只有一个元素，下图是 HashMap 的存储结构：（下标1位置的链表就只有一个元素）

 当下标 0 插入第 9 个元素，就会触发扩容的条件，但是由于 table 数组的⻓度小于 64，所以不会转为红⿊树。扩容和数据迁移后，存储结构变成如下所示：

 对第③种情况的代码分析如下：

 

② 树结构处理 split() 函数：

// 调用入口
else if (e instanceof TreeNode)
    ((TreeNode)e).split(this, newTab, j, oldCap);

// 【变量源码】
static final int UNTREEIFY_THRESHOLD = 6;

红⿊树的拆分⽅式与单向链表的拆分一样⼯，都是将⼀个整体拆分为⾼位和低位两部分。不同的是，拆分后的⾼低位双向链表中，如果数据⼩于等于6个，就不构成红黑树，而是构成链表。构成红黑树的目的是为了在大数据量的情况下能快速查询。但由于每次插⼊或者删除节点，都需要重新调整红⿊树的结构，以满⾜红⿊树的约束，所以，增删操作要慢于链表。所以，当元素很少的情况下，就直接采⽤链表的存储方式。下面分析在此过程中转为链表的 untreeify() 函数；和转为红黑树的 treeify() 函数。

untreeify() 函数：

final Node untreeify(HashMap map) {
    Node hd = null, tl = null;
    for (Node q = this; q != null; q = q.next) {
        Node p = map.replacementNode(q, null);
        if (tl == null)
            hd = p;
        else
            tl.next = p;
        tl = p;
    }
    return hd;
}
​
// 将树节点转换为链表节点
Node replacementNode(Node p, Node next) {
    return new Node<>(p.hash, p.key, p.value, next);
}

这部分代码就是遍历 TreeNode 双向链表，然后把每个节点转变为 Node 类型的节点，再拼装成⼀个单向链表。

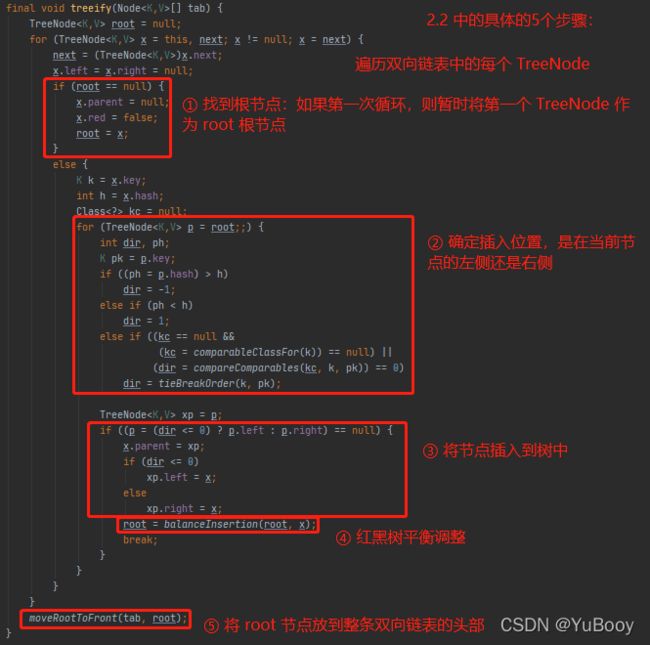
treeify() 函数：

这部分代码，跟前面【2.2 红黑树结构处理 中插入数据 putTreeVal()】内容是⼀样的。其实就是三个步骤：

● 步骤⼀：将待插⼊的节点插⼊到红⿊树中。

● 步骤⼆：由于树形结构变化了，所以要对红⿊树的平衡进⾏调整。

● 步骤三：如果由于对红⿊树进⾏了调整，有可能造成root节点的变化，那么就要把最新的root节点放到双向链表的头部，并插⼊到table数组中。

 

3> 如超过阈值，则进行扩容

// putVal() 方法的最后
if (++size > threshold)
    resize();

⼀直往 HashMap 中插⼊元素，总会有把 table 数组填满的时候，当 table 数组中数据越多，哈希冲突就越容易发⽣。为了减少这种情况发⽣，table 会根据约定好的阈值，即总容量的 2/3 或 0.75，如果超过了这个阈值，则会进⾏ table 数组的扩容操作。扩容函数 resize() 的解析：① 扩容准备【详看：1> 创建 table 数组】；② 数据迁移【详看：2.3）向单向链表中插入元素】

参考：长文多图——HashMap源码解析（包含红黑树）

PS：面试问题：多线程死循环问题（1.7从头插入；1.8从尾插入）

详见：jdk1.7 HashMap的死循环与jdk1.8 HashMap的优化_lzf的博客-CSDN博客