树学习笔记
树学习笔记
本文参考以及引用内容来自——数据结构(C语言版)—清华大学出版社—严蔚敏，吴伟民)
纯学习用，如有侵权请私信我告知！
一、树的定义
树的定义:
- 含有n(n ≥ 0)个节点的有限集合;
- 有且只有⼀个根节点;
- 当n > 1时，其他节点可分为 m (m > 0)个互不相交的有限集合T1,T2,…,Tm, 其中每⼀个集合本⾝⼜构成⼀棵树，并且称为根的子树。
即，子树之间是互不相交的集合。
结点(Node):
- 结点的度数(Degree of Node): 节点拥有的⼦树的数目
- 叶⼦结点(Leaf Node): 度为0的结点
- 孩⼦结点(Child Node): 某结点的⼦树的根结点称为该结点的孩⼦节点, ⽽该结点是这些孩⼦结点的⽗结点(Parent).
- 兄弟结点(Sibling Node): ⼀个⽗结点下的所有孩⼦结点之间互相称为兄弟结点.
- 结点的层次: 根为第⼀层; 若某结点在第l层, 则其⼦结点在l+1 层.
树的深度: 结点的最⼤层深为树的深度.
有序树: 树中结点的⼦树的顺序不能改变
路径: 从⼀个结点如何到达另⼀个结点. (只能是从根结点到⼦的⽅向)。
树的抽象数据类型：
ADT Tree<T> {
数据:D={di | di 属于 T , i = 0,1,..,n, n≥0}
关系:R={若D为空或只有⼀个元素, R为空;
否则R={ H (前驱关系) } :
1)存在唯⼀⼀个元素root,在 H 中⽆前驱;
2)对于D-{root},有⼀个将其分为若干个不想交⼦集的划分Di;每个⼦集
中有唯⼀⼀个元素和root构成前驱关系<root, xi>.
3)对应上述Di的划分,H-{<root,xi>}有唯⼀⼀个不想交的划分,且对任意的i,{Di, {Hi}}
是⼀棵符合本定义的树,{Di, {Hi}}成为root的⼦树.
对数据的操作(只列核⼼操作):
TraverseTree(…);
InsertNode(…);
DeleteNode(…);
TreeDepth(…);
Successor(…);
PreDecessor(…);
Parent(…);
Find(…);
};
二、二叉树
二叉树是一棵每个节点最多只能有两个子节点的有序树。
⼆叉树的基本性质
- ⼆叉树的第i层最多有 2^(i-1)个结点(i ≥ 1).
- 深度为k的⼆叉树，最多有2k-1个结点(k ≥ 1).
满二叉树：如果一棵二叉树有2^k-1个节点，该二叉树被称为满二叉树。
完全二叉树：如果一棵二叉树深度为h，则前h-1层都是满的，最后一层节点从左到右排序，则该二叉树被称为完全二叉树。
完全二叉树由满二叉树延伸出来，形似一个缺失右下角的三角形。 - ⾮空⼆叉树上叶⼦结点树等于度为2的结点数+1
三、二叉树的表示与实现（顺序和链式）
1.二叉树的顺序实现
二叉树的顺序实现，本质上就是创建一个数组，将树中的每个节点通过与该树对应的完全二叉树的节点编号和数组下标对应起来，从而达到用数组存储二叉树的目的。
但是数组在存储非完全二叉树时会浪费很多空间（数组中间会有很多被分配的空间没有被利用）。
2.二叉树的链式实现
二叉树的链式实现，将使用二叉链表。
节点设置两个指针，分别指向当前节点的左儿子和右儿子：
template<typename ElemType>
struct Node {
ElemType data;
Node* l_child, *r_child;
};
二叉树本身由一个指向根节点的指针表示。
template<typename ElemType>
class Binary_Tree {
Node<T>* root;
//其他操作
};
二叉树的操作：
CreateTree(String) : 根据所给”序列”构造⼆叉树, “序列”格式
应对应所构造⼆叉树的完全⼆叉树
CreateTree( ) : 根据⽤户输⼊构造⼆叉树, ⽤户输⼊格式为所
构造⼆叉树的完全⼆叉树
DestroyTree( ) : 销毁⼀棵树, 释放分配给其所含结点的内存
DestroyTree( )//层序遍历将节点放进队列，然后从根节点开始依次释放空间
if (root ==NULL) return;
L<Node*>.push_back(root); //L is a queue.
while(L not empty)
node = L.pop_front();
if(node == NULL) continue;
L.push_back(node->l_child);
L.push_back(node->r_child);
delete node;
LevelOrderTraverse( … ) : 层序遍历(宽度优先遍历BFS)
LevelOrderTraverse( )//继承destoryTree的思路
if (root ==NULL) return;
L<Node*>.push_back(root); //L is a queue.
while(L not empty)
node = L.pop_front();
if(node == NULL) continue;
L.push_back(node->l_child);
L.push_back(node->r_child);
visit(node); //访问node结点的数据
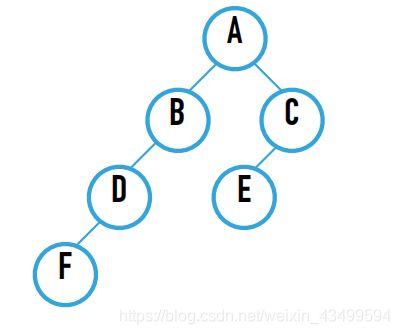
CreateTree(String) : 根据所给”序列”构造⼆叉树, “序列”格式按照待构造⼆叉树所对应的完全⼆叉树形式给出，假设 输⼊序列: A,B,C,D,#,E,#,F（#表示该位置的节点为空）
CreateTree(List s)
root = NULL;//根节点
if (s is empty) return;//如果队列为空则返回
idx = 0;//用来对应当前该读的子节点的下标
root = new Node(s[idx++], NULL, NULL);//初始化根节点
L.push_back(root); //L is a queue.//队列用来存储及遍历根节点
while( idx < s.length)
node = L.pop_front();//从队列中取出第一个元素
if (node == NULL) { idx += 2; continue;}
a = s[idx++];//取该节点对应下一个节点的值
if ( a != ‘#’) //如果为空，则将左儿子赋为空节点
node->l_child = new Node(a, NULL, NULL);
L.push_back(node->l_child); //将该值赋给左节点
if ( idx >= s.length) break;
a = s[idx++];//取该节点对应下一个节点的值
if ( a != ‘#’)//如果为空，则将右儿子赋为空节点
node->r_child = new Node(a, NULL, NULL);
L.push_back(node->r_child);//将该值赋给右节点
3.二叉树的遍历
1）递归遍历
所谓的中序、前序、后序，指的是当前节点对于其左⼦树和右⼦树的访问顺序，即先访
问⾃⼰,然后左,最后右（前序）; 还是先左,⾃⼰,最后右（中序）；还是先左,后右,最后⾃⼰（后序）
InOrderTraverse( … ) : 中序遍历⼀棵⼆叉树
InOrderTraverse( Node *p)
if (p ==NULL) return;
InOrderTraverse(p->l_child);
visit(p);
InOrderTraverse(p->r_child);
PreOrderTraverse( … ) : 前序遍历⼀棵⼆叉树
PreOrderTraverse(Node *p)
if(p==NULL) return;
visit(p);
PreOrderTraverse(p->l_child);
PreOrderTraverse(p->r_child);
PostOrderTraverse( … ) : 后序遍历⼀棵⼆叉树
PostOrderTraverse(Node *p)
if(p==null) return;
PostOrderTraverse(p->l_child);
PostOrderTraverse(p->r_child);
visit(p);
2）⼆叉树遍历的⾮递归版
此处引用于二叉树遍历之非递归算法，使用辅助栈来实现。
前序遍历的非递归版:
void preOrderIter(struct node *root)
{//按照当前节点，右儿子，左儿子的顺序压栈，利用栈先进后出的性质实现中→左→右的遍历
if (root == NULL) return;
stack<struct node *> s;
s.push(root);//根节点压栈
while (!s.empty()) {
struct node *nd = s.top();//取出节点并打印
cout << nd->data << " ";
s.pop();
if (nd->right != NULL)
s.push(nd->right);//右儿子压栈
if (nd->left != NULL)
s.push(nd->left);//左儿子压栈
}
cout << endl;
}
中序遍历的⾮递归版
void inOrderIter(struct node *root)
{
stack<struct node *> s;
while (root != NULL || !s.empty()) {
if (root != NULL) {
s.push(root);
root = root->left;
}
else {//此时已访问到最左下节点
root = s.top();
cout << root->data << " "; //访问完左子树后才访问根结点
s.pop();
root = root->right; //访问右子树
}
}
cout << endl;
}
}
后序遍历的非递归版
void postOrderIter(struct node *root)
{
if (!root) return;
stack<struct node*> s, output;
s.push(root);//压入根节点
while (!s.empty()) {
struct node *curr = s.top();//记录当前根节点
output.push(curr);
s.pop();
//先左后右进栈，之后会先右后左的进output，达到左→右→中的目的
if (curr->left)
s.push(curr->left);
if (curr->right)
s.push(curr->right);
}
while (!output.empty()) {
cout << output.top()->data << " ";
output.pop();
}
cout << endl;
}
3）⼆叉树的三叉链表实现的中序遍历
三叉链表的深度遍历，依然可以使⽤递归来完成。整个过程和⼆叉链表版本没有任何区别。
但是因为有了指向⽗亲的指针，我们可以写出⼀个迭代版本的中序遍历，即不⽤递归也不⽤辅助栈。
思路：
- 找到⼆叉树最左下的结点p;
- visit§; p = inorder_successor§;
- 返回2),直到 p 没有后继(p == NULL).
⼆叉树的三叉链表实现的中序遍历(⾮递归,不⽤栈)
//中序遍历,⾮递归,不⽤栈
void inOrder_No_Stack() {
if(root == NULL) {
print “空树”;
return;
}
cur = find_most_left_node(root);
do{
visit(cur)
cur = inOrder_Successor(cur);
}while(cur != NULL);
}
//对⾮空的结点p，找其最左下的结点
Node* find_most_left_node(Node *p) const {
while(p->l_child != NULL){
p = p->l_child;
}
return p;
}
//对⾮空的结点x，找其中序遍历下的后继结点
Node* inOrder_Successor(Node *x) const {
if(x->r_child != NULL)//如果x有右⼉⼦，则所求⼀定是其x的右⼦树中最左下的点
return find_most_left_node(x->r_child);
//否则就是x的祖先结点中的某⼀个.
p = x->parent;
while(p != NULL && x == p->r_child){ //如果为右节点，则应当已经被遍历过，往一个双亲结点回溯
x = p;
p = p->parent;
}
return p;
}
4.线索⼆叉树
1）线索二叉树的概念
二叉树节点的前驱和后继：中序遍历时的前一个或者后一个节点。
我们求二叉树的前序、中序、后序序列的时候，都必须用递归遍历相应的二叉树，或者借助栈等结构来记录。这样的话，如果我们想很快的找到某个节点在某种序列下的前驱或后继，每次都要遍历，这显然十分浪费时间。为了节省时间，可以把所有节点的前驱和后继记录下来，需要时可以直接查记录。但这种行为是用空间换时间下，需要单独分配存储前驱和后继信息的节点。
与此同时，用二叉链表构造的二叉树空链域的个数总是大于非空链域。假设一个二叉树一共有n个节点，则其拥有2n个链域。除了根节点以外的节点都有一个父节点，也就相当于有1条边，则n个节点的二叉树一共有n-1条边，即非空链域有n-1个，相对的，空链域有n+1个。
可以利⽤这些空指针把某个节点的前驱和后继记录下来：对于⼀个结点,如果左⼉⼦为空,那么左⼉⼦指向中序前驱(线索指针),如果右⼉⼦为空,则让它指向中序后继(线索指针)。
注意事项:
1.某个结点没有左/右⼉⼦时,才能成为线索指针;
2.⼀个结点,如果有左线索,那么其指向该结点的前驱; 右线索(如果有)则指向其后继;
3.第⼀个结点和最后⼀个结点没有前驱和后继(或者说他们的前驱和后继是NULL)
2）线索二叉树的存储结构
需要单独设置两个标志域来区分该节点的左右指针是否为线索
template<typename T>
struct Thread_Node {
bool l_thread, r_thread;//分别表⽰左右指针是否为线索.false表⽰不是.
Thread_Node *l_child, *r_child;
};
3）线索二叉树的遍历
1.线索二叉树的非递归遍历
通过设置左右线索，只需要找到该二叉树最左下的节点（即中序遍历所要输出的第一个节点），后面可以通过读后继来遍历整棵二叉树。
//中序线索遍历,⾮递归,不⽤栈
void inOrder_thread() const {
if(root == NULL) {
print "Empty tree.";
return;
}
Thread_Node <T>* cur = find_most_left_node_thread(root); //找到最左下的节点
do{
visit(cur);
cur = inOrder_successor_thread(cur);//找该节点的后继
}while(cur != NULL);
}
//对⾮空的结点x，找其中序遍历下的后继结点
//如果x的右⼉⼦不是线索，则x的中序后继⼀定是其右⼦树最左下的点
//否则x的右⼉⼦是线索指针，正好指向x的中序后继
Thread_Node <T>* inOrder_successor_thread(Thread_Node <T> *x) const {
if(x->r_thread != true)
return find_most_left_node_thread(x->r_child);
return x->r_child;
}
//对⾮空的结点p，找其最左下的结点，左⼉⼦不是线索，则⼀定有左⼉⼦
Thread_Node <T>* find_most_left_node_thread(Thread_Node <T> *p) const {
while(p->l_thread != true){
p = p->l_child;
}
return p;
}
2.线索二叉树的递归遍历
//中序线索遍历的建⽴,递归,把visit()换成建⽴线索
void inOrder_threading(Thread_Node <T>* p,Thread_Node <T>*& pre) const
{
if(p){//p不是空的
inOrder_threading(p->l_child, pre); //递归左⼦树
if(p->l_child == NULL) {
p->l_thread = true;
p->l_child = pre;
}
if(pre != NULL && pre->r_child == NULL){
pre->r_thread = true;
pre->r_child = p;
}
pre = p;
inOrder_threading(p->r_child, pre);
}
}
//中序线索遍历的建⽴,主调函数
void inOrder_threading() const {
if(root){//root不是空的
Thread_Node <T>* pre = NULL;
inOrder_threading(root, pre);
pre->r_thread = true;//线索化最后⼀个结点
pre->r_child = NULL;
}
}
5.二叉搜索树
1）、二叉搜索树的概念
性质及定义：
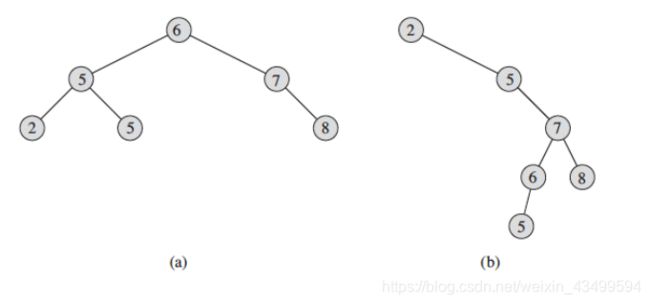
- T⾸先是⼀课⼆叉树,2) 如果x是⼆叉搜索树的⼀个节点，那么对所有来⾃其左⼦树的节点y，有y.key <= x.key；对于其所有来⾃其右⼦树的节点y，有y.key >= x.key.
即，某个节点的左子树所有节点都比它的值小，右子树所有节点都比它的值大。对⼀颗⼆叉搜索树进⾏中序遍历，可按⼤⼩顺序打印出所有元素。
查询元素时，如果值比当前节点的值小，则转左子树，反之则转右子树。
1.插入节点
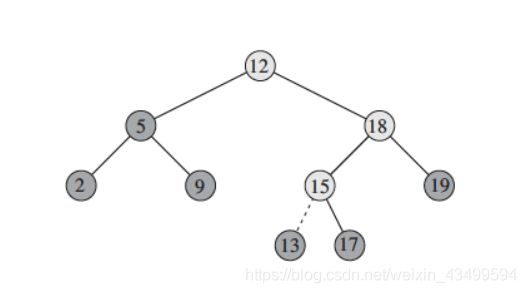
和查询的方法相似，如果要插入的值比当前节点的值小，则转左子树，反之则转右子树。
2.删除节点
从树T中删除一个节点z有三种情况：
- 该节点没有孩子，将其父节点指向它的指针直接置为NULL
- 该节点只有一个孩子，将这个孩子提升为它父节点的孩子，取代它的位置
- 该节点有两个孩子，寻找该节点的中序后继y（必在右子树里），将中序后继对应的节点y提升为其父节点的孩子，z中右子树剩下的部分成为y的新的右子树，z的左子树成为y的新左子树。 (第三种情况⽐较⿇烦，取决于y是不是z的右孩⼦)
Transplant(T, u, v):在T中，⽤以v为根的⼦树替换以u为根的⼦树。
⼆叉搜索树的插⼊、删除、查询，最⼤值、最⼩值都是O(h),h为树⾼.