数据结构与算法-Part6——数组与广义表
目录
一丶数组
1：一维数组
2：二维数组
1）二维数组的概念
2）二维数组的顺序存储结构
3）二维数组的遍历
3：在C#中自定义矩阵类
二丶稀疏矩阵
1：稀疏矩阵的三元组
2：稀疏矩阵三元组集合的顺序存储结构
1）稀疏矩阵的顺序存储结构三元组类
2）基于三元组顺序存储结构的稀疏矩阵类
3：稀疏矩阵三元组集合的链式存储结构
三丶广义表
1：广义表的概念及定义
2：广义表的特性和操作
1）广义表的特性
2）广义表的操作
3：广义表的图形表示
4：广义表的存储结构
1）基于单链表示的广义表
2）基于双链表示的广义表
数组是一种基本而又重要的数据集合，一个数组对象是由一组具有相同类型的数据元素组成的集合，数据元素按次序存储与一个地址连续的内存空间中。
一维数组可以看作是一个顺序存储结构的线性表，二维数组则可以视为数组的数组。
一般采用二维数组存储矩阵，但这种方法存储特殊矩阵和稀疏矩阵的效率较低，需采用一些特殊的方法进行压缩处理。
一丶数组
数组是一种重要的基础性数据集合，是其他数据结构实现顺序存储的基础，它的对象可以是由一组相同类型的数据元素组成的集合，也可以是复杂的用户自定义类型。
逻辑上数组可以看成二元组<下标，值>的集合 ，以后还会有二元组<键，值>的集合（哈希表）
1：一维数组
一维数组是由n个相同类型的数据元素
构成的有限序列，n称为数组长度。任意一个元素在序列中的位置可由其数组下标标识，通过数组名加下标的形式可以访问数组中任一指定元素。
假设数组的首地址是
,每个数据元素占用c个存储空间，则第i个数据元素的地址为：
该操作的复杂度是O（1），数组是一种随机存储结构
一般由两种为数组分配内存空间的方式：
1）编译时分配数组空间：源程序中声明数组时给出数组元素类型和个数。当程序开始时，数组即获得系统分配的一块连续地址的内存空间
2）运行时分配数组空间：源程序声明数组时，仅说明数组元素类型，不指定数组长度。当程序运行中需要使用数组时，向系统申请指定长度数组所需的存储单元空间。在C#中，数组都是在运行时分配所需空间。
更多有关数组的属性方法，见博客：
零基础自学C#——Part2：C#中的运算符、语句、类型转换、数据结构_代码历险记的博客-CSDN博客
2：二维数组
1）二维数组的概念
二维数组可以看作是元素为一维数组的数组，三维数组可以看成是由二维数组组成的数组。
2）二维数组的顺序存储结构
假设每个数据元素占有c个存储空间，
为元素ai,aj的存储地址，
为首元素的地址，即起始地址，可以由两种方式实现二维数组的顺序存储：
①一种是按行优先次序存储（行主序，row major order），则元素
的地址计算函数为：
②另一种是按列优先次序存储（列主序，column major order），则元素的地址计算函数为：
3）二维数组的遍历
一维数组只有一种遍历方式，而二维数组则有两种基本遍历次序：
①行优先次序遍历：对二维数组依行序逐行访问每个数据元素
②列优先次序遍历：对二维数组依列序逐列访问每个数据元素
更多有关二维数组的属性和方法见：
零基础自学C#——Part2：C#中的运算符、语句、类型转换、数据结构_代码历险记的博客-CSDN博客
3：在C#中自定义矩阵类
在普遍的使用中，应多设计通用和专用的矩阵类对矩阵数据的处理带来效率提升
例：自定义矩阵类及矩阵的相加操作
本例声明Matrix类来表示矩阵对象，类中成员items是一个元素类型为整型int的一堆数组，成员变量rows记录矩阵的行数，成员变量cols记录矩阵列数，设计了多个构造方法以便构造和初始化矩阵
Add()方法实现与另一个矩阵的相加操作，Transpaose()方法实现矩阵的转置操作。
public class Matrix //定义矩阵类
{
private int[] items; //私有一个int类的数组Items
private int rows,cols; //私有整型变量行数，列数
public Matrix(int nRows,int nCols) //声明一个矩阵，n行n列，内容为行数*列数
{
rows=nRows;
cols=nCols;
items=new int[rows*cols];
}
public Matrix(int nSize):this(nSize,nSize){}
public Matrix():this(1){}
public Matrix(int nRows,int nCols,int[] mat)
{
rows=nRows;
cols=nCols;
items=new int[rows*cols];
Array.Copy(mat,items,mat.Length);
}
public Matrix(Matrix omat)
{
rows=omat.Rows;
cols=omat.Columns;
int size=rows*cols;
items=new int[size];
Array.Copy(omat.items,this.items,size);
}
public int Rows
{
get{return rows;}
}
public int Columns
{
get{return cols;}
}
//获得或设置第i行第j列的元素
public int this[int i,int j]
{
get{return items[i*cols+j];}
set{items[i*cols+j]=value;}
}
//两个矩阵相加
public void Add(Matrix b)
{
for(int i = 0; i < Rows; i++)
{
for(int j=0;jMatrix类定义在Matrix.cs源文件中，同样也声明为DSA命名空间中，加法和转置操作程序如下：
using System;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
namespace matrixtest
{
public class MatrixTest
{
public static void Main(string[] args)
{
int[] m1={1,2,3,4,5,6,7,8,9};
Matrix a=new Matrix(3,3,m1);
a.Show();
Matrix b=new Matrix(3,3,m2);
b.Show();
a.Add(b);
a.Show();
Matrix c=a+b;
c.Show();
c.Transpose();
Matrix d=new Matrix(c);
d.Show();
}
}
}二丶稀疏矩阵
在工程计算中常常会出现一些阶数很高的矩阵，在这类矩阵中常常存在许多零元素或值相同的元素，如果对这类矩阵按常规方法存储会占用很大的存储空间，应该采用特殊的方法进行压缩存储以节省存储空间。
设一个n×m的矩阵有t个非零元素，则矩阵中非零元素占比为δ=t/(m×n)，当δ≤0.1时，称这类矩阵为稀疏矩阵(sparse matrix)
当矩阵中有很多零元素且非零元素具有某种分布规律时，可以只对非零元素进行顺序存储，此时仍可以对元素进行随机存取，如：下三角矩阵
0 ... 0
... 0
.... ..... .... ..
,....,
当i
,因此元素的地址可用下式计算：
![Addr(a_{i,j})=Addr(a_{0,0})+[\frac{i(i+1)}{2}+j]\times c](http://img.e-com-net.com/image/info8/95fbd232a2714890b2734f5df7b80f11.png){kind=small}
,其中0≤j≤j≤n-1
当矩阵中大多数元素值为0且非零元素的分布没有规律时，可以用顺序存储结构或链式存储结构表示非零元素的三元组
1：稀疏矩阵的三元组
稀疏矩阵的一个非零元素可以由一个三元组<行下标，列下标，矩阵元素值>来表示一个稀疏矩阵则可以用它的三元组集合表示，例如稀疏矩阵
A=[ 1 0 0 0
0 0 0 0
2 0 0 3
0 4 0 5] 可以用三元组序列表示为{0,0,1},{2,0,2},{2,3,3},{3,1,4},{3,3,5},即有非零元素的时候用它的行列数和它的本身值来表示，称为该三元
2：稀疏矩阵三元组集合的顺序存储结构
1）稀疏矩阵的顺序存储结构三元组类
为描述顺序存储结构的稀疏矩阵中表示非零元素的三元组，定义TripleEntry类：
namespace DSA
{
public class TripleEntry
{
private int row;
private int column;
private int data;
public TripleEntry(int i,int j,int k)
{
row= i;
column=j;
data=k;
}
public TripleEntry():this.(0,0,1){}
public int Row
{
get
{
return row;
}
set
{
row=value;
}
}
public int Column
{
get
{
return column;
}
set
{
column=value;
}
}
public int Data
{
get
{
return data;
}
set
{
data =value;
}
}
public void Show()
{
Console.WriteLine("r:"+row +"\t c:"+column+"\t v:"+data);
}
}
}用TripleEntry类型定义的实例表示稀疏矩阵的一个三元组，用来记录稀疏矩阵中的一个非零元素的行列位置和值
2）基于三元组顺序存储结构的稀疏矩阵类
下面声明的SSpareMatrix类表示基于三元组顺序存储结构的稀疏矩阵对象
using System;
using System.Collections.Generic;
namespace DSA
{
public class SSparseMatrix
{
private int rows,cols;
protected List items;//三元数组线性表
public int Row
{
get
{
return rows;
}
set
{
rows=value;
}
}
public int Columns
{
get
{
return cols;
}
set
{
cols=value;
}
}
public SSparseMatrix(int[,] mat)
{
Console.WriteLine("稀疏矩阵(二维数组):");
rows=mat.GetLength(0);
cols=mat.GetLength(1);
items=new List();
for(int i = 0; i < rows; i++)
{
for(int j = 0; j 三元组TripleEntry和稀疏矩阵SSParseMatrix类都定义了成员Show()方法，TripleEntey类中的Show()方法输出一个矩阵元素的三元组值，SSparseMatirx类中的Show()方法输出一个稀疏矩阵中所有的三元组
例：测试基于三元组顺序存储结构的稀疏矩阵类
using System;
using System.Collections.Generic;
namespace matrixtest
{
public class SSparseMatrixTest
{
public static void Main[string[] args]
{
//稀疏矩阵
int[,]mat={{1,0,0,0},{0,0,0,0},{2,0,7,0},{0,0,8,9}};
SSparseMatrix ssm=new SSparseMatrix(mat);
ssm.Show();
}
}
}
输出为矩阵所有元素
3：稀疏矩阵三元组集合的链式存储结构
稀疏矩阵的三元组集合可以用集中方式的链式存储结构来表示，例如基于行，基于列，和十字链表示等方法，下面介绍基于行的单链的方法来存储稀疏矩阵的三元组集合。
1）将稀疏矩阵每一行上的非零元素作为结点链接成一条单向链表
2）用一个数组记录这些链表，从上到下的元素依次指向各行第一个数据结点
为了以行的单链表示法描述稀疏矩阵，可以声明如下的两个类：三元组结点类LinkedTriple和链式存储结构稀疏矩阵类LSparseMatirx
namespace DSA
{
public class LinkedTriple
{
private int column;
private int data;
private LinkedTriple next;
public int Column
{
get
{
return column;
}
set
{
column=value;
}
}
public int Data
{
get
{
return data;
}
set
{
data=value;
}
}
public LinkedTriple Next
{
get
{
return next;
}
set
{
next=value;
}
}
public LinkedTriple(int i,int k)
{
column=i;
data=k;
next=null;
}
public LinkedTriple():this(0,1){}
public void Show()
{
LinkedTriple p=this;
while(p!=null)
{
Console.Write(" "+p.Column+" "+p.Data+"->");
p=p.Next;
}
Console.WriteLine();
}
}
}
三元结点类LInkedTriple定义链表结点的类型，它由三个成员组成：conlumn、data、next（用来引用后继节点）。 一个LInkedTriple类型的对象表示链表中的一个结点，对应于稀疏矩阵中的一个非零元素
下面定义LSparseMatrix稀疏矩阵类的一个构造方法将一个用二维数组表示的常规矩阵转换成行的单链表示，然后用SHow()依次输出
namespace DSA
{
public class LsparseMartix
{
LinkedTriple[] rowLink;
private int rows,cols;
public int Rows
{
get
{
return rows;
}
set
{
rows=value;
}
}
public int Columns
{
get
{
return cols;
}
set
{
cols=value;
}
}
public SparseMatrix(int[,] mat)
{
rows=mat.GetLength(0);
cols=mat.GetLength(1);
rowLink=new LinkedTriple[rows];
int i,j;
LinkedTriple p=null,q;
for(int i = 0; i < rows; i++)
{
p=rowLink[i];
for(j=0;j
例：基于行单链的稀疏矩阵实现
下面的程序调用LSparseMatrix类实现稀疏矩阵行的单链表示
using System;
namespace matrixtest
{
public class LSparseMatrixTest
{
public static void Main(string[] atgs)
{
int[,] mat={{1,0,0,0},{0,0,0,0},{2,0,0,3},{0,4,0,5}};
LSparseMatrix lsm=new LSparseMatrix(mat);
lsm.Show();
}
}
}
运行结果表示为：
Row Triples[0]=0 1->.
Row Triples[1]=.
Row Triples[2]=0 2 -> 3 3->.
Row Triples[3]=1 4 -> 3 5->
三丶广义表
1：广义表的概念及定义
线性表结构可以是简单的数组，也可以扩展为复杂的数据结构——广义表(general list)，广义表是n个元素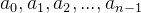组成的有限序列，记作：
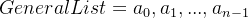
这里的广义表在结构复杂性上可以拓展，元素可以是不可再分的单元素，也可以是还可以再分的线性表或广义表，这些可以再分的元素称为子表。广义表所包含的数据元素的个数n称为广义表的长度。
广义表的元素为原子或子表，用小写字母表示原子，大写字母表示表和子表：
L1=( ) ：L1为空表
L2=（L1）=（（））：广义表L2包含一个子表元素L1，L2的长度为1
L=（1，2）：常规线性表L包含了两个（原子）元素，长度为2
T=（3，L）=（3，（1，2））：广义表T包含原子元素3和子表元素L，T的长度为2
在表示广义表时，可以将表明写在对应的括号前，这样即表明了每个表的名字，又说明了它的组成。广义表可以表示多层次的结构，它用递归的形式进行定义，广义表层次的深度即是广义表的深度
2：广义表的特性和操作
1）广义表的特性
①广义表可以作为其他广义表的子表元素
②广义表是一种多层次的结构
③广义表是一种广义的线性结构
④广义表可以递归
2）广义表的操作
用广义表的形式可以表示线性表、树、图等多种基本的数据结构，因此广义表的操作既包含与线性表、树、图等数据结构类似的基本操作，也包含一些特殊操作，主要有：
Initialize:初始化，建立一个广义表
IsAtom:判别某数据元素是否为原子
IsList:判别某数据元素是否为子表
Insert:插入
Remove:删除
Equals：判别两个广义表是否相同
Copy：复制
3：广义表的图形表示
1）广义表L的数据元素都是原子，元素对应的结点都是原子结点，则该广义表是具有线性特征的线性表
2）广义表数据元素既有原子，又有子表，但表中不存在共享和递归成分，该广义表为具有树结构特性的纯表。
3）广义表数据元素中有子表，且表中有共享存在，该广义表为具有图结构特性的再入表
4）广义表的数据元素有子表且有递归成分，该广义表为具有图结构特性的递归表
4：广义表的存储结构
具有线性特性的普通线性表有顺序存储结构和链式存储结构两种实现方式，具有层次结构的广义表则通常采用链式存储结构
1）基于单链表示的广义表
广义表可以用单向链表结构存储，有如下三个域构成
public class GSLinkedNode
{
public bool isAtom;
public object data;
public GSLinkedNode next;
其他成员
}
域isAtim是一个标志域，表示数据元素（结点）是否为原子，data存放数据值，Next成员存放与当前数据元素处于同层的下一个数据元素所对应结点的引用
2）基于双链表示的广义表
广义表也可以采用双向链表存储，由以下三个域组成：
public class GSLinkedNode
{
public T data;
public GSLinkedNode next;
public GSLinkedNode child;
其他成员
}
域child是子表中第一个数据元素所对应结点的引用，next则引用同与本数据元素处于同层的下一个数据元素所对应的结点