《机器学习》第5章 神经网络
文章目录
- 5.1 神经元模型
- 5.2 感知机与多层网络
- 5.3 误差逆传播算法
- 5.4 全局最小与局部最小
- 5.5 其他常见神经网络
-
- RBF网络
- ART网络
- SOM网络
- 级联相关网络
- Elman网络
- Boltzmann机
- 5.6 深度学习
5.1 神经元模型
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。
神经网络中最基本的成分是神经元模型,即上述定义中的简单单元。
M-P神经元模型

理想中的跃阶函数:

实际常用Sigmoid作激活函数:

把许多个这样的神经元按一定层次结构连接起来就形成了神经网络。
5.2 感知机与多层网络
感知机由两层神经元组成,如下图所示,输入层接收外界输入信号后传递给输出层,输出层是M-P神经元,亦称阈值逻辑单元。

感知机权重:


要解决非线性可分问题,需要考虑使用多层神经元.如下图简单的两层感知机就能解决异或问题,输入层与输出层之间的一层神经元被称为隐层或隐含层,隐含层和输出层神经元都是拥有激活函数的功能神经元。

每层神经元与下一层神经元完全互连,神经元之间不存在同层连接,也不存在跨层连接,这样的神经网络结构通常称为“多层前馈神经网络”。
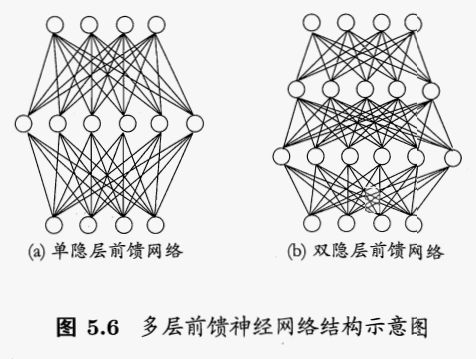
5.3 误差逆传播算法
误逆差传播算法(BP):训练多层网络,BP算法不仅可用于多层前馈神经网络,还可用于其他类型的神经网络。但通常说“BP网络”时,一般指用BP算法训练多层前馈神经网络。

假定神经网络的输出为:

则均方误差为:

确定参数:
网络中有(d+l+1)q+l个参数需确定:输入层到隐层的d × q个权值、隐层到输出层的q × l 个权值、q个隐层神经元的阙值、l个输出层神经元的阈值.BP是一个迭代学习算法,在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计。任意参数v的估计公式为:

缓解BP过拟合的两种方式:
- (1)早停:将数据分成训练集和验证集,训练集用来计算梯度、更新连接权和阈值,验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阈值。
- (2)正则化:在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权与阈值的平方和,则误差目标函数(5.16)改变为:

5.4 全局最小与局部最小
5.5 其他常见神经网络
RBF网络
RBF:径向基函数,是一种单隐层前馈神经网络,它使用径向基函数作为隐层神经元激活函数,而输出层则是对隐层神经元输出的线性组合。
假定输入为d维向量x,输出为实值,则RBF网络可表示为:



ART网络
竞争型学习是神经元网络中一种常用的无监督学习策略,在使用该策略时,网络的输出元神经相互竞争,每一时刻仅有一个竞争获胜的神经元被激活,其他神经元的状态被抑制。这种机制被称为“胜者通吃”原则。
ART:自适应协振理论,竞争型,该网络由比较层、识别层、识别阈值和重置模块构成。
比较层负责接收输入样本,并将其传递给识别层神经元。识别层每个神经元对应一个模式类,神经元数目可在训练过程中动态增长以增加新的模式类。
ART比较好的缓解了竞争型学习中“可塑性-稳定性窘境”,可塑性是指神经网络要有学习新知识的能力,而稳定性是指神经网络在学习新知识时要保持对旧知识的记忆。这就使得ART网络有一个很重要的优点:可进行增量学习或在线学习。
SOM网络
SOM:自组织映射,一种竞争学习型的无监督神经网络,它能将高维输入数据映射到低维空间,同时保持输入数据在高维空间的拓扑结构,即将高维空间中相似的样本点映射到网络输出层中的临近神经元。
SOM的训练过程很简单:在接收到一个训练样本后,每个输出层神经元会计算该样本与自身携带的权向量之间的距离,距离最近的神经元成为竞争获胜者,称为最佳匹配单元(best matching unit).然后,最佳匹配单元及其邻近神经元的权向量将被调整,以使得这些权向量与当前输入样本的距离缩小.这个过程不断迭代,直至收敛.

级联相关网络
一般的神经网络模型通常假定网络结构是事先固定的,训练的目的是利用训练样本来确定合适的连接权、阈值等参数.与此不同,结构自适应网络则将网络结构也当作学习的目标之一,并希望能在训练过程中找到最符合数据特点的网络结构.级联相关(Cascade-Correlation)网络[Fahlman and Lebiere, 1990]是结构自适应网络的重要代表.

与一般的前馈神经网络相比,级联相关网络无需设置网络层数、隐层神经元数目,且训练速度较快,但其在数据较小时易陷入过拟合.
Elman网络
与前馈神经网络不同,“递归神经网络”(recurrent neural networks)允许网络中出现环形结构,从而可让一些神经元的输出反馈回来作为输入信号.这样的结构与信息反馈过程,使得网络在t时刻的输出状态不仅与t时刻的输入有关,还与t―1时刻的网络状态有关,从而能处理与时间有关的动态变化.










