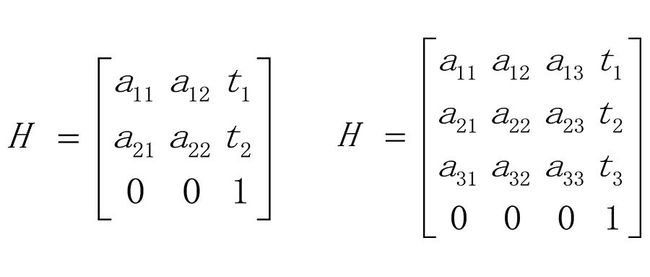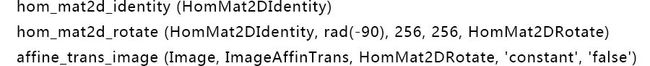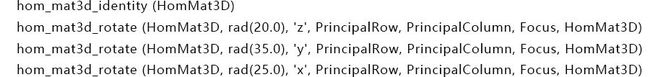halcon中相似变换、仿射变换、投影变换的区别以及应用方式和例程
在机器视觉系统中,镜头是重要成像部件之一,而基于小孔成像原理的工业镜头往往会产生透视畸变现象,如何校正畸变是进行图像分析的前提 ,这其中就会用到投影变换,也是几何变换的一种。除此之外,图像处理中常用到的平移、旋转、缩放等,也属于几何变换。本文将通过实例详细介绍HALCON中的几何变换。
基础知识
齐次坐标(Homogenous Coordinate)
齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。例如二维点p(x,y)àp(x,y, w)就成了齐次坐标,同理三维点p(x,y,z)àp(x,y,z, w)也成了齐次坐标。显然,齐次坐标的表达并不是唯一的,随w值的不同而不同。在计算机图学中,w 作为通用比例因子,它可取任意正值,但一般在几何变换中,总是取w=1。齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易于进行几何变换。
以点p(x,y)为例,如果想把它平移至p(x+a,y+b),是不可能用矩阵计算完成的,现在换成齐次坐标(x,y,1),通过矩阵相乘(左侧公式) ,很方便得到平移后的坐标(x+a,y+b)。通常把变换矩阵写到左侧,为了保持一致把变换矩阵改成右下角形式,这就是齐次变换矩阵。
齐次变换矩阵
在同一变换矩阵中既表示姿态(旋转、缩放等)又表示位置(平移),这种形式的矩阵称为齐次变换矩阵。如下:
齐次坐标的使用,使得几何变换更容易计算,尤其对于仿射变换(二维/三维)更加方便,由于图形硬件、视觉算法已经普遍支持齐次坐标与矩阵乘法,因此更加促进了齐次坐标使用,使得它成为图形学中的一个标准,下面提到的几何变换(仿射变换)都以齐次坐标和齐次变换矩阵为基础。
几何变换
几何变换包括:
相似变换(Similarity Transformation)
仿射变换(Affine Transformation)
投影变换(Projective Transformation)
注:线性变换不包含平移,所以没有归入几何变换,总之HALCON中常用几何变换是仿射和投影变换,而相似变换是仿射变换的一种简单情况!相似变换、仿射变换、投影变换既可以发生在二维空间内也可发生在三维空间内。
相似变换
相似变换的定义:由一个平面/立体图形变换到另一个平面/立体图形,在改变的过程中保持形状不变(大小方向和位置可变),任何相似变换都可以分解为等比例缩放、平移、旋转的组合,例如,对于缩放,用齐次变换矩阵可以如下表示(二维和三维),其中a≠0。
仿射变换
仿射变换的定义:由一个平面/立体图形变换到另一个平面/立体图形,在改变的过程中保持直线和平行线不变(平行线映射为平行线),任何仿射变换都可以分解为缩放、平移、旋转和切变(Shearing)的组合,对于仿射变换,齐次变换矩阵如下表示(二维和三维):
对于仿射变换,有两个比较特殊的变换:非等比例缩放和切变(如下图),除了这两个特殊的变换之外,相似变换可以看做是仿射变换的特殊形式,注:线性变换包括旋转、缩放、切变,但不包含平移,因此仿射变换也定义为一个线性变换再加上一个平移变换。
投影变换的定义:变换过程中,直线映射为直线(但不一定保证平行度),任何二维投影变换都可以用3x3可逆矩阵表示,而任何三维投影变换都可以用4x4可逆矩阵表示。如下:
从定义来看,仿射变换可以看做是投影变换的特殊形式。另外,把投影变换矩阵的最后一行变为[0,0,1]或者[0,0,0,1],即可变为仿射变换矩阵,也可以证明仿射变换是投影变换的特殊形式。因此,对于平移、缩放、切变等,仿射变换和投影变换都可以实现。
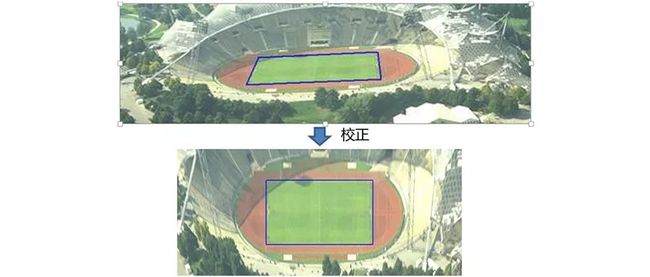
如下例子,把左图进行旋转操作变成右图,可以用仿射变换和投影变换两种方式实现。
仿射变换实现方法
投影变换实现方法之一
(直接用给定点生成投影变换矩阵)
-
投影变换实现方法之二
(用三维仿射变换矩阵生成投影变换矩阵)
-
注:对于旋转来说,也可以看做是相机沿Z轴旋转90度后的成像效果,因此也可以用三维仿射变换,先转换相机坐标系,再生成投影变换矩阵!
旋转示例中的仿射变换矩阵(也是齐次变换矩阵)
旋转示例中的投影变换矩阵(3X3),也是可逆矩阵
同理,缩放、切变等,仿射变换和投影变换也都可以实现,但如下变换,只能用二维投影变换矩阵实现,因为变换过程中没有保证线的平行性。
总结
HALCON中所用的变换知识只涉及到了二维、三维仿射变换和二维投影变换,二维仿射变换多用于平面图像的平移、旋转、缩放等;三维仿射变换多用于三维坐标系的平移、旋转等(或者用3D位姿表示),而二维投影变换多用于校正透视畸变,也就是三维空间的景象如何投影到相机靶面上的效果,如果相机和被测平面不垂直就会有畸变。
在成像过程中,普通工业镜头(小孔成像原理)都会带来透视畸变,也就是常见的近大远小现象,除非相机和被测平面保持绝对垂直,否则透视畸变是不可避免的。因此,通过三维空间的仿射变换(变换坐标系,使相机不垂直于被摄平面),可以产生透视畸变效果,也就是相当于进行了投影变换,HALCON也提供了算子hom_mat3d_project,能直接把三维仿射变换矩阵转换成二维投影变换矩阵(4x4的矩阵转换成3x3矩阵)。下面我们通过一个例子来说明一下。
首先生成单位矩阵,进行一系列的旋转变换,产生三维仿射变换矩阵,也就是使得相机和被摄平面不垂于!
把三维仿射变换矩阵再转化成二维投影变换矩阵
![]()
进行投影变换,也就是我们看到的右侧的效果
![]()
另外一种方法是,直接使用给定点生成投影变换矩阵,可以得到同样的效果
上面的这个例子是很好的说明了透视畸变现象如何产生的,左侧图是相机垂直于被摄平面,没有透视变形现象。然后进行了一系列的三维仿射变换,产生的效果就是相机不再垂直于被摄面,所以右图产生了透视畸变现象,那么从左图到右图恰恰是进行了一次二维投影变换。因为投影变换矩阵是可逆的,所以也可以把右图校正为左图,这恰恰是HALCON中投影变换的用处所在!
以下例子也是HALCON中典型的畸变校正示例,使用的正是投影变换。
附录
解释一下HALCON中的:
hom_mat2d_*和hom_mat3d_*算子
hom_mat2d_identity产生2x3矩阵,用于描述二维变换,实际上是3x3齐次变换矩阵(仿射变换);
hom_mat3d_identity产生3x4矩阵,用于描述三维变换,实际上是4x4齐次变换矩阵(仿射变换);
hom_mat2d_*既支持2x3矩阵(仿射变换)也支持3x3矩阵(投影变换);
hom_mat3d_*支持3x4矩阵(仿射变换),也就是4x4齐次变换矩阵
关于如何在HALCON中生成的:
仿射变换矩阵和投影变换矩阵
仿射变换矩阵
用hom_mat2d_identity或hom_mat3d_identity产生单位矩阵,然后经过平移、旋转、缩放等操作后得到仿射变换矩阵。
投影变换矩阵
hom_mat3d_project能直接把三维仿射变换矩阵转换成投影变换矩阵,如果知道空间坐标系是如何变换的,可以用这种方法;
hom_vector_to_proj_hom_mat2d用给定点生成投影变换矩阵,输入点的坐标为三维齐次坐标,可以支持无穷远点和有限远点的变换;
vector_to_proj_hom_mat2d用给定点生成投影变换矩阵,输入点为二维非齐次坐标,支持有限远的点的变换;
注:对于涉及有限远点的变换,以上两个算子都可以!
最后给出halcon的投影变换实例:2d_data_codes_rectify_symbol.hdev
例子中用到的图像:
接着是正文具体代码:
*参考例子:
*投射变换和二维码识别:2d_data_codes_rectify_symbol.hdev
*轮廓转线及调整直线:measure_metal_extended.hdev(例子中还有调整弧线,本例没有用到)
dev_set_draw ('margin')//设置填充模式
read_image (Image, 'code2d')//获取图片
threshold (Image, Region, 10, 90)//通过阈值分割,获取二维码的区域
shape_trans (Region, RegionTrans, 'convex')//把区域的边缘连接起来
gen_contour_region_xld (RegionTrans, Contours, 'border')//区域转轮廓
segment_contours_xld (Contours, ContoursSplit, 'lines', 5, 10, 1)//把轮廓断开成线
XCoordCorners := []//保存四边形的顶点X坐标
YCoordCorners := []//保存四边形的顶点Y坐标
*对轮廓进行排序,不排序会影响投射变换操作
sort_contours_xld (ContoursSplit, SortedRegions, 'lower_left', 'true', 'row')
count_obj (SortedRegions, Number)//获取区域数量
for Index := 1 to Number by 1
select_obj (SortedRegions, ObjectSelected, Index)//遍历区域
*把弯线变直
fit_line_contour_xld (ObjectSelected, 'tukey', -1, 0, 5, 2, RowBegin, ColBegin, RowEnd, ColEnd, Nr, Nc, Dist)
gen_contour_polygon_xld (Contour, [RowBegin,RowEnd], [ColBegin,ColEnd])//画线看效果
tuple_concat (XCoordCorners, RowBegin, XCoordCorners)//保存X轴数据
tuple_concat (YCoordCorners, ColBegin, YCoordCorners)//保存y轴数据
endfor
*标记出记录的点
gen_cross_contour_xld (Crosses, XCoordCorners, YCoordCorners, 6, 0.785398)
*获取投射变换参数HomMat2D
hom_vector_to_proj_hom_mat2d (XCoordCorners, YCoordCorners, [1,1,1,1], [70,270,270,70], [100,100,300,300], [1,1,1,1], 'normalized_dlt', HomMat2D)
*对图像进行投射变换
projective_trans_image (Image, Image_rectified, HomMat2D, 'bilinear', 'false', 'false')
*以下为对二维码的识别
create_data_code_2d_model ('Data Matrix ECC 200', [], [], DataCodeHandle)
find_data_code_2d (Image_rectified, SymbolXLDs, DataCodeHandle, [], [], ResultHandles, DecodedDataStrings)
clear_data_code_2d_model (DataCodeHandle)
area_center_xld (SymbolXLDs, Area, Row, Column, PointOrder)
*显示二维码解析到的数据
disp_message (3600, DecodedDataStrings, 'window', Row+160, Column-100, 'black', 'true')