力扣刷题-动态规划算法3:完全背包问题
目录
- 1. 完全背包问题概念
- 2. 完全背包问题第一种:求最大价值(和题目描述一致)
- 3. 完全背包问题第二种:求最多的组合(类似0-1第二种)
- 4. 完全背包的总结
-
- 4.1 第一类完全背包问题::求最大价值
- 4.2 第二类完全背包问题:装满可能性
- 4.3 0-1背包和完全背包的区别:就在重量是否是正逆序上面。
- 第一题:518.零钱兑换II(完全背包第二类问题:组合数)
- 第二题:377.组合总和IV(完全背包第二类问题,考虑排列数)
- 第三题:70.爬楼梯(完全背包第二类问题,考虑排列数)
- 第四题:322.零钱兑换(完全背包第一类问题,求最小值)
- 第五题:279.完全平方数(完全背包第一类问题,求最小值)
- 第六题:139.单词拆分?(完全背包第一类问题,求可能不可能)
- 7. 多重背包问题
- 8. 总结:
1. 完全背包问题概念
-
问题描述:
1)有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。
2)每件物品都有无限个(也就是可以放入背包多次)(比0-1背包多出的条件)
3) 求解将哪些物品装入背包里物品价值总和最大。 -
求解步骤:
1)首先遍历物品,然后遍历重量,都是从小到大遍历,顺序没有关系(因为性价比最高的只有一个)
2. 完全背包问题第一种:求最大价值(和题目描述一致)
- 代码
//1. 先遍历物品,再遍历重量最常见,也更好理解一点
public class demo2 {
public static void main(String[] args) {
int[] weight = new int[]{1, 3, 4};
int[] value = new int[]{15, 20, 30};
int maxweight = 4;
//1)dp数组的定义,默认初始化零
int[] dp = new int[maxweight + 1];
//2)遍历和迭代:先物品再重量,是正序
for (int i = 0; i < weight.length; i++) {
for (int j = weight[i]; j <= maxweight ; j++) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
System.out.println("dp=" + Arrays.toString(dp));
}
}
//2. 先遍历重量,再遍历物品
public class demo2 {
public static void main(String[] args) {
int[] weight = new int[]{1, 3, 4};
int[] value = new int[]{15, 20, 30};
int maxweight = 4;
//1)dp数组的定义,默认初始化零
int[] dp = new int[maxweight + 1];
//2)遍历和迭代:先重量再物品,是正序
for (int j = 0; j <= maxweight ; j++) {
for (int i = 0; i < weight.length; i++) {
if(j>=weight[i]) dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
System.out.println("dp=" + Arrays.toString(dp));
}
}
3. 完全背包问题第二种:求最多的组合(类似0-1第二种)
题目描述:容量为k背包,存放物品int[] coins,装满有多少种可能性(每种物品有无限个)
注意:遍历先物品还是先重量是有区别的:
1)先物品再重量,那么就是组合数
//1. 求组成的种类,因为是完全背包,故重量也是从小到大
public int change(int amount, int[] coins) {
//1)dp数组的定义和初始化
int[] dp =new int[amount+1];
dp[0]=1;
//2)dp数组遍历和迭代 //迭代公式一定要记住,是一个累加的过程。
for(int i=0;i<coins.length;i++){
for(int j=coins[i];j<=amount;j++){
dp[j]+=dp[j-coins[i]];
}
}
return dp[amount];
}
1)先重量再物品,那么就是排列数
//1. 求组成的种类,因为是完全背包,故重量也是从小到大
public int change(int amount, int[] coins) {
//1)dp数组的定义和初始化
int[] dp =new int[amount+1];
dp[0]=1;
//2)dp数组遍历和迭代 //迭代公式一定要记住,是一个累加的过程。
for(int j=0;j<=amount;j++){
for(int i=0;i<coins.length;i++){
if(j>=coins[i]) dp[j]+=dp[j-coins[i]];
}
}
return dp[amount];
}
4. 完全背包的总结
4.1 第一类完全背包问题::求最大价值
1)问题描述:若干个物品,每个物品有对应的重量和价值,当背包大小固定为K时,如何装存物品,使得背包中物品的价值最大?其中同一种物品的个数不限制。
2)求解方法:
(1):用一维dp数组:使用默认初值0;双层遍历,先正序遍历物品,再正序遍历重量或者先正序遍历重量,再逆序遍历物品,两种遍历方向都可以,但是必须都为正序遍历。
4.2 第二类完全背包问题:装满可能性
1)问题描述:容量为k背包,存放物品,装满有多少种可能性?其中同一种物品的个数不限制。
2)求解方法:
(1):用一维dp数组:dp[0]=1;双层遍历
先正序遍历物品,再正序遍历重量,迭代方法为累加,求的是组合数;
先正序遍历重量,再正序遍历物品,迭代方法为累加,求的是排列数。
4.3 0-1背包和完全背包的区别:就在重量是否是正逆序上面。
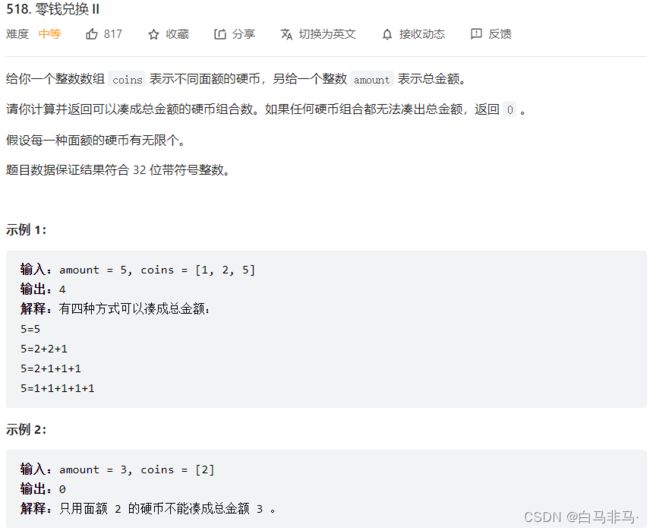
第一题:518.零钱兑换II(完全背包第二类问题:组合数)
- 题目描述
 ```
```
2. 步骤
1)就是第二类完全背包问题,求背包满的种类数,只是这里用了组合数,所以需要先遍历物品,再遍历重量。
4. 代码
```java
//1. 求组成的种类,因为是完全背包,故重量也是从小到大
public int change(int amount, int[] coins) {
//1)dp数组的定义和初始化
int[] dp =new int[amount+1];
dp[0]=1;
//2)dp数组遍历和迭代 //迭代公式一定要记住,是一个累加的过程。//先物品再重量
for(int i=0;i第二题:377.组合总和IV(完全背包第二类问题,考虑排列数)
public int combinationSum4(int[] nums, int target) {
//定义dp数组,并初始化
int[] dp=new int[target+1];
dp[0]=1;
//迭代遍历:先金额,再硬币种类
for(int i=0;i<=target;i++){
for(int j=0;j<nums.length;j++){
if(i>=nums[j]) dp[i]+=dp[i-nums[j]];
}
}
return dp[target];
}
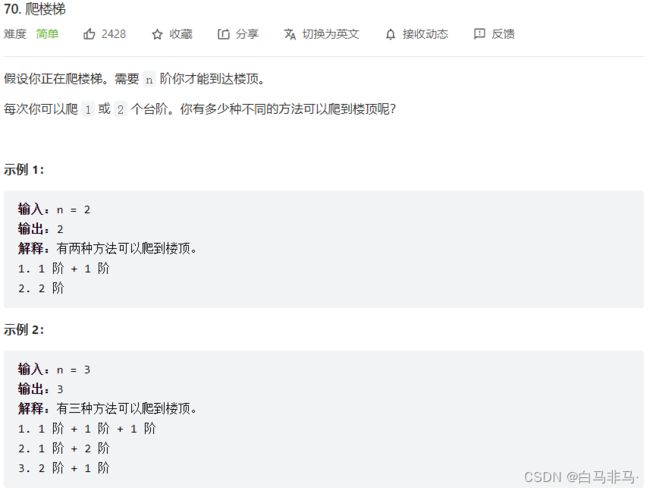
第三题:70.爬楼梯(完全背包第二类问题,考虑排列数)
- 题目描述
- 解题思路
1)这是之前出现的一道题目,用斐波那契算法类似的。
2)也可以从完全背包方面进行解析。 - 代码
//以前的思路
public int climbStairs(int n) {
//1)斐波那契算法
int[] dp=new int[n+1];
if(n<=2) return n;
dp[0]=0;
dp[1]=1;
dp[2]=2;
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
//完全背包的思路
public int climbStairs(int n) {
//完全背包问题:两个物体【1和2】,背包的大小为n,物品的个数为无限
//求解符合要求的情况有多少种,求排列数
//1)dp数组的定义和初始化
int[] dp=new int[n+1];
dp[0]=1;
//2)遍历和迭代:先背包,后物品,正序
for(int i=0;i<=n;i++ ){
for(int j=1;j<=2;j++){
if(i>=j) dp[i]+=dp[i-j];
}
}
return dp[n];
}
第四题:322.零钱兑换(完全背包第一类问题,求最小值)
- 题目描述
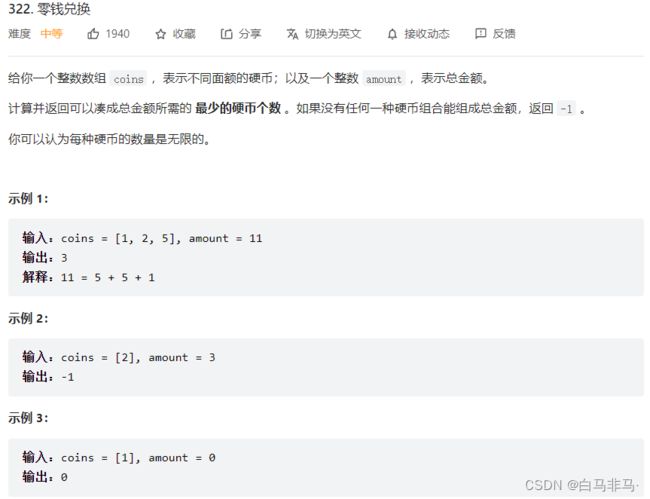
- 解题步骤
1)先遍历物品,再遍历钱;
2)dp[ i] 数组的含义为:为了凑成总金额所需的最少硬币个数
3)迭代公式:
(1):加入硬币i,故其硬币总数为:dp[ j-weight[ i ] ]+1
(2):不加入硬币i,故其硬币维持之前的为:dp[ j ] - 代码
class Solution {
public int coinChange(int[] coins, int amount) {
//核心思路:这是一个典型的完全背包问题,两层遍历,从前向后,只是迭代公式不一样
//迭代公式:dp[j]=Math.min(dp[j],dp[j-coins[i]]+1)
//dp数组的新建和初始化(第一个为0,剩下的初始为最大值max)
int max=Integer.MAX_VALUE;
int[] dp=new int[amount+1];
for(int i=1;i<amount+1;i++){
dp[i]=max;
}
//System.out.println("dp1="+ Arrays.toString(dp));
//遍历(没有顺序)
for(int i=0;i<coins.length;i++){
for(int j=coins[i];j<=amount;j++){
//易错点:如果退回去的值dp[j-coins[i]]=max,那么这一步就不算数
if(dp[j-coins[i]]!=max) dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);
}
//System.out.println("dp="+ Arrays.toString(dp));
}
//返回判断:如果最后时max,则不能够组成
return dp[amount]==max?-1 : dp[amount] ;
}
}
- 注意点:
1)初始化数组的时候,因为要比较的是最小值,所以第一个值初始化为0,后面的初始化应该为比较大的值(相对于于比较最大值的区别)
2)在中间比较的时候,当之前的硬币数数有效时,即不是初始值的时候,才是有效的,进行判断才有价值。
第五题:279.完全平方数(完全背包第一类问题,求最小值)
- 题目描述
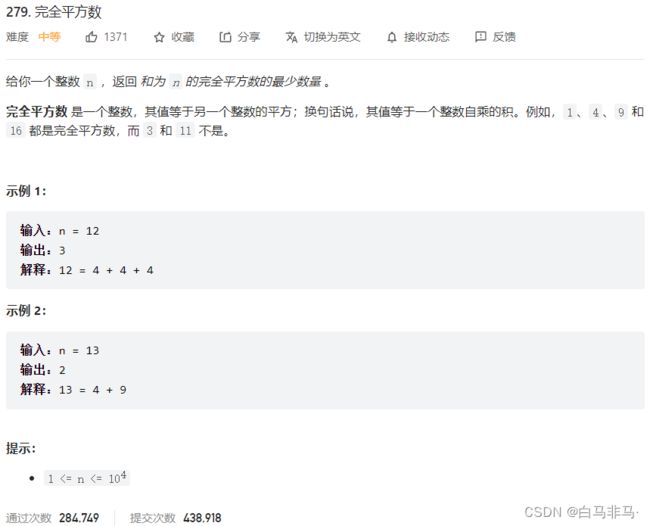
- 解题步骤
1)此题和上一题一模一样,只是需要通过给定的n,然后自己给出物品数组 - 代码
class Solution {
public int numSquares(int n) {
//1)根据给定的值,得出物品的集合
int[] things=new int[n+1];
for(int i=1;i<=n;i++) things[i]=i*i;
//System.out.println(Arrays.toString(things));
//2)初始化dp数组
int max=Integer.MAX_VALUE;
int[] dp=new int[n+1];
for(int i=1;i<=n;i++) dp[i]=max;
//System.out.println(Arrays.toString(dp));
//3)遍历和迭代
for(int i=1;i<=n;i++){
for(int j=things[i];j<=n;j++){
if(dp[j-things[i]]!=max) dp[ j ]=Math.min(dp[j-things[i]]+1, dp[j]);
}
}
//4)输出
return dp[n];
}
}
第六题:139.单词拆分?(完全背包第一类问题,求可能不可能)
- 题目描述
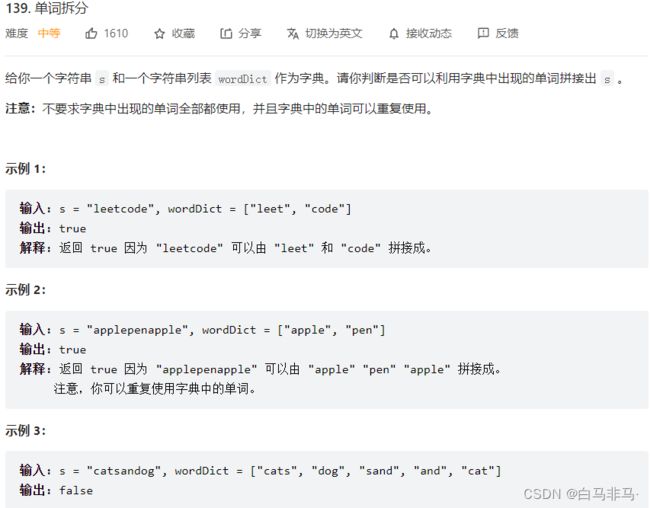
- 解题步骤
1)dp[i] :即从0-i个字符,是否都在wordDict里面能够找到对应的值;可能是全部,可能是一部分。
2)迭代公式:
(1):把s的前i个字符分为两部分:如果前面一部分已经判断能够找到,剩下的一部分能够凑成一个单词,那么就可以判定为true了。
3)遍历顺序:遍历背包放在外循环,将遍历物品放在内循环。内循环从前到后。 - 代码
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
//完全背包问题:数组就是硬币,字符串就是金钱
//1)数组的定义和初始化:boolean[] 默认值为false;
boolean[] dp=new boolean[s.length()+1];
dp[0]=true; //dp[0]=true;
//2)遍历迭代:先重量,后物品
for(int i=1;i<=s.length();i++){ //**遍历背包**
for(int j=0;j<i;j++) //**遍历物品**
//前一部分 dp[j]=s.substring(0,j+1)在字典中能够找到
//后一部分:wordDoct.contains(s.substring(j,i) 能够找到对应的单词
if( dp[j] && wordDict.contains(s.substring(j,i)) ) dp[i]=true;
}
//3)输出:
return dp[s.length()];
}
}
7. 多重背包问题
- 有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
- 与0-1背包问题区别:0-1背包问题每件物品个数为1,而多重背包为设定的值x
- 求解思路:直接在0-1背包问题上面进行改写:先遍历物品,再遍历重量,然后再加一层循环,即遍历物品的个数,就可以解出来了。
8. 总结:
- 完全背包第二类问题:求解装满背包的种类:
(0):迭代公式:dp[j] += dp[j - nums[i]]
(1):组合数:518.零钱兑换II
(2):排列数:377.组合总和IV,70.爬楼梯 - 完全背包第一类问题:问装满背包所有物品的最小个数:
(0):dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
(1):322.零钱兑换
(2):279. 完全平方数
