【数据结构-树】C语言实现哈夫曼树及哈夫曼编码

存储结构

//哈夫曼树存储结构 
typedef struct
{
	int weight;
	int parent,lchild,rchild;
}HTNode,*HuffmanTree;

查找算法

//查找算法
void Select(HuffmanTree HT,int end,int *S1,int *S2)
{
	int min1,min2;   //记录最小的两个权值   min1比min2要小 
	int j,i=1;
	while(HT[i].parent != 0 && i<=end)   //结点的双亲值不为0继续循环找到等于0的结点为止 
		i++;
	min1 = HT[i].weight;   //第一个双亲值为0的结点的权 
	*S1 = i++;   //先复制后自加，记录这个结点在哈夫曼树储存表里的位置 
	while(HT[i].parent !=0 && i<=end)    //同样结点双亲值为0继续循环 
		i++;
	if(HT[i].weight < min1)   //比较两个结点的权，min1储存最小的，min2储存较大的 
	{
		min2 = min1;
		*S2 = *S1;
		min1 = HT[i].weight;
		*S1 = i;
	}
	else     //否则直接给min2 
	{
		min2 = HT[i].weight;
		*S2 = i;
	}
	//用最先找到的两个没有双亲的结点和后面的进行比较
	for(j=i+1;j<=end;j++)
	{
		if(HT[j].parent != 0) continue;   //不为0的跳过 
		if(HT[j].weight < min1)  //比最小的min1还小，就重新赋值给最小的min1 
		{
			*S2 = *S1;
			min2 = min1;
			*S1 = j;
			min1 = HT[j].weight;
		}
		else if(HT[j].weight>=min1 && HT[j].weight<min2)   //注意=表达的意思，即和最小的权一样时赋值给min2 
		{
			*S2 = j;
			min2 = HT[j].weight;
		}
	}
}

创建哈夫曼树

//创建哈夫曼树
void CreateHuffmanTree(HuffmanTree *HT,int n)
{
	//初始化工作 
	if(n<=1) return;
	int m = 2*n-1;   //一棵哈夫曼树总有2n-1个结点 
	*HT = (HuffmanTree)malloc(sizeof(HTNode)*(m+1));     //从1开始，所以有m+1个   malloc返回首元素地址——HuffmanTree类型指针 
	for(int i=1;i<=m;++i)
	{   //初始化 
		(*HT)[i].parent = 0;
		(*HT)[i].lchild = 0;
		(*HT)[i].rchild = 0;
	}
	for(int i=1;i<=n;++i)   //循环输入权值 
		scanf("%d",&((*HT)[i].weight));   //如果是（A，weight）类型，可以自定义结构体类型
	
	//开始创建哈夫曼树
	for(int i=n+1;i<=m;++i)
	{
		int S1,S2;   //S1、S2是最小值和次最小值在数组里的下标
		Select(*HT,i-1,&S1,&S2);   //调用函数找出最小的那两个 
		(*HT)[S1].parent = i;   //给最小的那两个的双亲值赋值 
		(*HT)[S2].parent = i;
		(*HT)[i].lchild = S1;   //给新结点添加孩子位置 
		(*HT)[i].rchild = S2;
		(*HT)[i].weight = (*HT)[S1].weight + (*HT)[S2].weight;   //新结点等于俩孩子权值之和 
	}
}

以权值[1,2,3,4,5]为例，哈夫曼树（其一）如下：

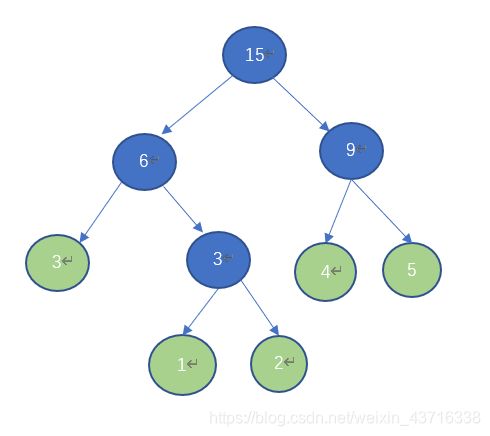
建立以下哈夫曼树存储结构。

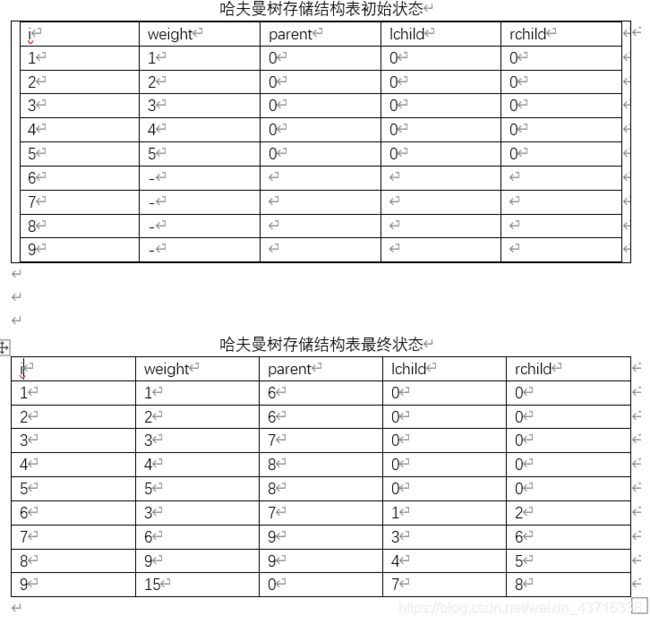
创建哈夫曼编码表

void CreateHuffmanCode(HuffmanTree HT,HuffmanCode *HC,int n)
{
	int start,i;
	*HC = (HuffmanCode)malloc(sizeof(char *)*(n+1));   //哈夫曼编码表，元素值是指向char类型的指针 
	char *cd = (char *)malloc(sizeof(char)*n);        //结点元素编码表，临时存储叶子结点逆序至根结点的编码 
	cd[n-1]='\0';   //添加字符串结尾符 
	for(i=1;i<=n;++i)
	{
		start = n-1;  //从倒数第二开始 
		int c=i;     //当前叶子节点位置，赋值给c变量，c——孩子 （child） 
		int f=HT[i].parent;     //当前叶子结点的双亲结点位置   f——双亲（father and mother） 
		while(f!=0)  //双亲不为0继续循环 
		{
			--start;   //因为数组从0开始，所以倒数第二表示为n-2=start 
			if(HT[f].lchild == c) cd[start]='0';   //是否等于该双亲结点的左孩子 
			else cd[start]='1';    //否则等于该双亲的右孩子 
			c=f;   //回溯，双亲结点也是它双亲的孩子（双重身份） 
			f=HT[f].parent;  //找到它双亲位置 
		}
		(*HC)[i] = (char *)malloc(sizeof(char)*(n-start));    //用当前编码数创建一个等数内存储存该编码串，并把地址传给哈夫曼编码表（存放指针变量）存放 
		strcpy((*HC)[i],&cd[start]);   //复制 
	}
	free(cd);
}

接着以上哈夫曼树，表如下：

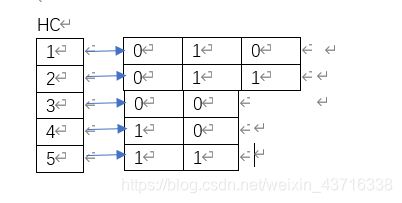
运行结果：

代码整合测试

#include 
#include 
#include 

typedef char **HuffmanCode;   //二重指针，用于创建哈夫曼编码表 

//哈夫曼树存储结构 
typedef struct
{
	int weight;
	int parent,lchild,rchild;
}HTNode,*HuffmanTree;

//查找算法
void Select(HuffmanTree HT,int end,int *S1,int *S2)
{
	int min1,min2;   //记录最小的两个权值   min1比min2要小 
	int j,i=1;
	while(HT[i].parent != 0 && i<=end)   //结点的双亲值不为0继续循环找到等于0的结点为止 
		i++;
	min1 = HT[i].weight;   //第一个结点的双亲值为0的权 
	*S1 = i++;   //先复制后自加，记录这个结点在哈夫曼树储存表里的位置 
	while(HT[i].parent !=0 && i<=end)    //同样结点双亲值为0继续循环 
		i++;
	if(HT[i].weight < min1)   //比较两个结点的权，min1储存最小的，min2储存较大的 
	{
		min2 = min1;
		*S2 = *S1;
		min1 = HT[i].weight;
		*S1 = i;
	}
	else     //否则直接给min2 
	{
		min2 = HT[i].weight;
		*S2 = i;
	}
	//用最先找到的两个没有双亲的结点和后面的进行比较
	for(j=i+1;j<=end;j++)
	{
		if(HT[j].parent != 0) continue;   //不为0的跳过 
		if(HT[j].weight < min1)  //比最小的min1还小，就重新赋值给最小的min1 
		{
			*S2 = *S1;
			min2 = min1;
			*S1 = j;
			min1 = HT[j].weight;
		}
		else if(HT[j].weight>=min1 && HT[j].weight<min2)   //注意=表达的意思，即和最小的权一样时赋值给min2 
		{
			*S2 = j;
			min2 = HT[j].weight;
		}
	}
}

//创建哈夫曼树
void CreateHuffmanTree(HuffmanTree *HT,int n)
{
	//初始化工作 
	if(n<=1) return;
	int m = 2*n-1;   //一棵哈夫曼树总有2n-1个结点 
	*HT = (HuffmanTree)malloc(sizeof(HTNode)*(m+1));     //从1开始，所以有m+1个   malloc返回首元素地址——HuffmanTree类型指针 
	for(int i=1;i<=m;++i)
	{   //初始化 
		(*HT)[i].parent = 0;
		(*HT)[i].lchild = 0;
		(*HT)[i].rchild = 0;
	}
	for(int i=1;i<=n;++i)   //循环输入权值 
		scanf("%d",&((*HT)[i].weight));
	
	//开始创建哈夫曼树
	for(int i=n+1;i<=m;++i)
	{
		int S1,S2;
		Select(*HT,i-1,&S1,&S2);   //调用函数找出最小的那两个 
		(*HT)[S1].parent = i;   //给最小的那两个的双亲值赋值 
		(*HT)[S2].parent = i;
		(*HT)[i].lchild = S1;   //给新结点添加孩子位置 
		(*HT)[i].rchild = S2;
		(*HT)[i].weight = (*HT)[S1].weight + (*HT)[S2].weight;   //新结点等于俩孩子权值之和 
	}
}

//哈夫曼编码
void CreateHuffmanCode(HuffmanTree HT,HuffmanCode *HC,int n)
{
	int start,i;
	*HC = (HuffmanCode)malloc(sizeof(char *)*(n+1));   //哈夫曼编码表，元素值是指向char类型的指针 
	char *cd = (char *)malloc(sizeof(char)*n);        //结点元素编码表，临时存储叶子结点逆序至根结点的编码 
	cd[n-1]='\0';   //添加字符串结尾符 
	for(i=1;i<=n;++i)
	{
		start = n-1;  //从倒数第二开始 
		int c=i;     //当前叶子节点位置，赋值给c变量，c——孩子 （child） 
		int f=HT[i].parent;     //当前叶子结点的双亲结点位置   f——双亲（father and mother） 
		while(f!=0)  //双亲不为0继续循环 
		{
			--start;   //因为数组从0开始，所以倒数第二表示为n-2=start 
			if(HT[f].lchild == c) cd[start]='0';   //是否等于该双亲结点的左孩子 
			else cd[start]='1';    //否则等于该双亲的右孩子 
			c=f;   //回溯，双亲结点也是它双亲的孩子（双重身份） 
			f=HT[f].parent;  //找到它双亲位置 
		}
		(*HC)[i] = (char *)malloc(sizeof(char)*(n-start));    //用当前编码数创建一个等数内存储存该编码串，并把地址传给哈夫曼编码表（存放指针变量）存放 
		strcpy((*HC)[i],&cd[start]);   //复制 
	}
	free(cd);
}

int main()
{
	int i;
	int n=5;
	HuffmanTree HT;   //哈夫曼树指针变量 
	HuffmanCode HC;   //哈夫曼编码指针（二重指针） 
	CreateHuffmanTree(&HT,n);    //创建哈夫曼树 
	CreateHuffmanCode(HT,&HC,n);  //创建哈夫曼编码表 
	for(i=1;i<=n;i++)   //位置一样的，所以遍历即可 
	{
		printf("%d: ",HT[i].weight);
		printf("%s\n",HC[i]);  //HC[i]是编码串首地址值，%s格式时首地址就可以 
	}
	return 0;
}