浅谈BFS使用与设计
目录
前言
那些疑问:BFS为什么可以求取最短路?
以题磨“剑”
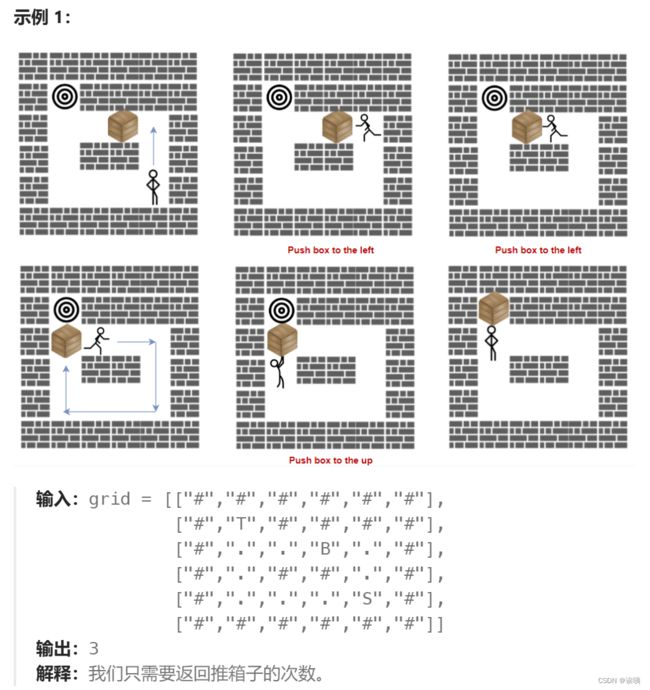
题1:迷宫与宝藏
思路解析
AC代码
题2:推箱子
思路解析
AC代码(以Leetcode为例)
引用资料
前言:
在阅读本文时,默认读者对BFS算法,宽度优先搜索算法,有所了解以及理解。BFS算法的思路,代码实现本文不给出。还望海涵,本文的创作是源于一些进阶的BFS使用。后续还会有所更新。
闲言少叙,书归正传。让我们进入正题!
那些疑问:BFS为什么可以求取最短路?
我相信大家在首次接触到BFS算法的时候,算法课老师肯定会说明BFS可以用于求解最短路径问题。但是大部分老师却不愿意说道说道为什么BFS可以求取最短路?
我希望可以通过抛出我手头的“砖块”,引出大家伙手中的“玉石”,欢迎各位在评论区留下自己的见解。以下是我个人的见解:
首先,面对BFS算法的思路,我觉得最为贴切的描述就是“水漫金山式搜索”。以“起点”为水源,向外逐步扩散,这有点像MC中水的扩散方式。
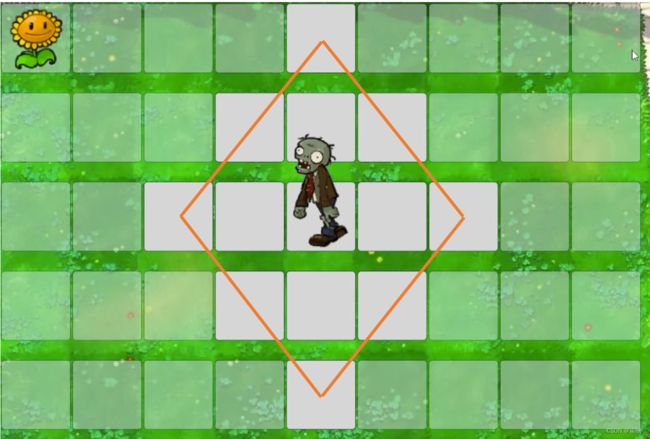
举一个简单的例子:僵尸吃向日癸。
我们已知僵尸每秒可以移动 1 步,现在僵尸想知道自己最少需要几步(秒)可以吃到向日葵。同时规定在第 0 秒时,僵尸在某一位置,称为“起点”。向日癸的位置称为“终点”。
那么在第 1 秒钟末时,僵尸可以走到的位置使用灰色方块标出。从中我们可以发现,最远位置就是灰色方块的边界。
同理,当时间来到第 2 秒末时,僵尸可以走到的范围(灰色方块)如下图所示,其中最远可以抵达的地方也是灰色方块的边界。
以此类推,我们可以知道当灰色方块恰好覆盖到向日癸所在位置,即终点时的时间就是我们需要的答案。这是符合人类直观想法的说明方式。
(注:图片来自B站UP主 -- 打工人小棋的影视资料,链接放在文末,推荐大家观看优质资源)
但是如果在挖的深层次一些。如何“专业化”?这里我们注意到一个特点:最优性+单调性!这是问题得以解释的根源。最优性就是僵尸第 n 秒末时可以抵达的最远位置,而单调性可以视为一种检索与判定,如果一旦判定到终点包含在最优状态内,那么程序终止。
以题磨“剑”
题1:迷宫与宝藏
题目描述:
机器人要在一个矩形迷宫里行动(不能原地停留,只能走向上/下/左/右),每移动一格花费1个单位时间。 迷宫有以下几种元素: 【*】 机器人的起点 【#】 墙。机器人不能走过这些格子 【.】 平地。机器人可以在上面自由行走 【0-9】 宝藏。当机器人走到此处会立刻获得该数字相应的宝藏,宝藏不会消失,可以反复获取(但不能停留) 若机器人要恰好获得总和为x的宝藏,它最少需要多少时间?
输入要求:
第一行输入任务数量T, 接下来有T个任务 每块第一行有两个整数, n(0≤n≤100), m(0≤m≤100), 表示迷宫有n+1行和m+1列 接下来n+1行输入迷宫 最后一行输入你要收集的宝藏的总价值x(x ≤ 100)
输出要求:
对于每个任务,输出最少花费的时间,如果完成不了该任务则输出-1
样例1:
样例输出:
思路解析
首先,这道题是一道“最短/长代价”的题目,同时与图挂钩。所以,我们很自然能够想到使用BFS,或者说是动态规划(DAG规划)。但是这道题存在一个难点,就是每个位置可以重复访问。这意味着我们不能够使用 vis 数组进行剔除操作。因为原版BFS中的剔除操作无效化,使得这道题看起来具有无穷性!这也是上述难点的根本问题 -- 无穷性。面对无穷性,我们可以考虑使用 链表来表示循环无穷性,以及分析题目是否存在上确界,或者变换描述使得状态有限化。根据上述三个策略的描述,我们可以很快分析出策略1,链表表示,不适合。所以我们可以考虑接下来两种策略。其次就是因为题目给出的要求是恰好为 x ,所以,上确界不存在。
至此,我们考虑变换描述使得状态有限化。但是注意,我们还有一个重要线索 -- 采取BFS算法 + 动态规划。所以,我们需要关注到两个算法特性,首先动态规划的特性显然是可以轻易满足的。所以,我们重点考虑BFS算法的特性:最优性 + 单调性。因为动态规划和BFS都涉及最优性质,所以在这个性质上,我们不需要特别考虑。因此,我们的考虑重心来到单调性。
在原版BFS中,单调性的体现在“步数”上。但是,我们之前分析过,如果使用步数的单调性会产生无穷性。所以,我们需要做出改变,我们不能使用步数的单调性。而是采取其他状态的单调性。而除了步数以外,具有单调性的状态就是“金币数量”。故此,我们应当考虑使用“金币数量”。在结合动态规划。我们可以很快设计出状态 Step[x][y][money]。 Step[x][y][money] 表示在 (x, y) 处获得money 个金币数量的最小步数。依照BFS核心思路:根据单调性扩展,不断更新状态到最优。
AC代码
#include
#include
#include
#include
#include
#include
#define MAX_N 105
#define MAX_M 105
#define MAX_X 105
#define INF 0x3F3F3F3F
int T, n, m, x;
int Step[MAX_N][MAX_M][MAX_X];
int Map[MAX_N][MAX_M];
const int direct[4][2] = { {1, 0} , {-1, 0} , {0, 1} , {0, -1} };
struct Info {
int x, y, money;
};
std::queue que;
inline bool check(int x, int y) {
return 0 <= x && x <= n && 0 <= y && y <= m && Map[x][y] != INF;
}
int BFS() {
while (!que.empty()) {
Info cur_status = que.front();
que.pop();
for (int i = 0; i < 4; ++i) {
int nxt_x = cur_status.x + direct[i][0];
int nxt_y = cur_status.y + direct[i][1];
if (check(nxt_x, nxt_y)) {
int nxt_money = cur_status.money + Map[nxt_x][nxt_y];
if (nxt_money == x) return Step[cur_status.x][cur_status.y][cur_status.money] + 1;
if (nxt_money > x) continue; // 大于x的不需要继续往下检索,因为money单调增
// case: < x
if (Step[nxt_x][nxt_y][nxt_money] > Step[cur_status.x][cur_status.y][cur_status.money] + 1) {
Step[nxt_x][nxt_y][nxt_money] = Step[cur_status.x][cur_status.y][cur_status.money] + 1;
que.push({nxt_x, nxt_y, nxt_money}); // 压入更新状态
} // 更新发生时
} // 合法状态
} // 尝试四个方向
}
return -1; // 无法完成任务
}
int main() {
scanf("%d", &T);
while (T--) {
memset(Map, 0, sizeof Map);
memset(Step, 0x3F, sizeof Step);
scanf("%d%d", &n, &m);
char ch;
for (int i = 0; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
scanf(" %c", &ch);
if (ch == '#') Map[i][j] = INF;
else if (ch == '*') {
Step[i][j][0] = 0;
que.push({ i, j, 0 });
}
else if (ch == '.') ; // 空地不做处理--空语句
else Map[i][j] = ch - '0';
}
} // 读入地图
scanf("%d", &x);
printf("%d\n", BFS()); // 输出答案
} // solution
return 0;
} 题2:推箱子
题目描述:
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m * n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
- 玩家用字符
'S'表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。 - 地板用字符
'.'表示,意味着可以自由行走。 - 墙用字符
'#'表示,意味着障碍物,不能通行。 - 箱子仅有一个,用字符
'B'表示。相应地,网格上有一个目标位置'T'。 - 玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
- 玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
样例:
思路解析
有了第一题的训练,我们知道BFS关注单调性和最优性。在推箱子中,我们仍然可以将题目抽象为“图的最短路问题”。但是,这里的难点是箱子的移动被做出了限制!导致单调性被破坏。为了方便理解这件事情,我们简单地说明一下。如果按照原版的“步数”来实现,我们就有两种“步数” -- 人的步数,箱子的步数。二者缺一不可,因为箱子的步数被人的限制。所以,我们会有二元组(box_step, man_step) 但是人物每一次移动(状态更新)并不意味着box_step + 1。所以,在压入队列时,二元组不一定存在单调性。这可能会导致代码错误。特别注意,我们说的单调性是指队列中是单调的。在理论上该二元组一定是具有单调性的,但是在实际的压入过程中是难以保证的,因为这与更新状态的压入次序有关,我们不能保证单调性与压入次序相关。
所以,为了实现二元组在队列中具有单调性,我们可以使用优先队列。但是这会增加时间复杂度。可以视具体数据规模而定。
在这里,我不打算讲解使用优先队列的解决方案。因为比较简单,只需要相关状态记录的时候按照(box_step, man_step)二元组排序即可。那么,我们来考虑一下其他的思路,可以更高效的处理该问题。
推箱子这类题目中,最重要的是某一个元素是我们的关注核心,但是另外一个就稍显不足道。或者说是作为“约束”出现的。所以,我们重点来考虑箱子。容易发现,每一次箱子移动时,人物位置必然在箱子的未移动的位置上!所以,我们可以考虑上述情况绑定成一个状态。当两个物体被绑定成一个时,我们的思路就简单了,因为我们可以对整体进行原版BFS--在方向上(队列中)单调性。但是,还没有结束。直接对整体BFS跟对箱子直接BFS没有区别,因为这忽略了局部元素--人产生的影响。所以,对整体状态判定、更新时,我们需要考虑人的可达性。
状态更新时,只需要压入(移动后箱子的位置, 未移动时箱子位置/移动后人的位置)。值得注意的是,人的推动位置是 “此状态箱子位置” - dir数组, 箱子的移动位置是 “此状态箱子位置” + dir数组。
AC代码(以Leetcode为例)
leetcode. 1263 推箱子
class Solution {
private:
int dir[4][2] = { {0,1},{0,-1},{1,0},{-1,0} };
struct Point {
int x, y;
bool operator==(const Point& other) const {
return x == other.x && y == other.y;
}
void operator=(const Point& other) {
x = other.x;
y = other.y;
}
bool operator!=(const Point& other) const {
return x != other.x || y != other.y;
}
};
struct state {
Point box, people;
state(Point box, Point people) : box(box), people(people){};
};
public:
int minPushBox(vector>& grid) {
const int m = grid.size();
const int n = grid[0].size();
Point t, b,s;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'T') {
t.x = i, t.y = j;
}
else if (grid[i][j] == 'B') {
b.x = i, b.y = j;
}else if (grid[i][j] == 'S') {
s.x = i, s.y = j;
}
}
}
//-----------------定义需要的函数--------------
auto check = [&](Point x) -> bool {
return 0 <= x.x && x.x < m && 0 <= x.y && x.y < n && grid[x.x][x.y] != '#';
};
auto bfs = [&](Point& star, Point& pur, Point &box) -> bool {
vector > vis(m, vector(n, 0));
vis[star.x][star.y] = 0;
queue _que;
_que.push(star);
Point move;
while (!_que.empty()) {
Point curr = _que.front();
_que.pop();
if (curr == pur) return true;
for (int i = 0; i < 4; ++i) {
move.x = curr.x + dir[i][0], move.y = curr.y + dir[i][1];
if (check(move) && move != box && !vis[move.x][move.y]) {
_que.push(move);
vis[move.x][move.y] = 1;
}
} // 尝试四个方向移动
}
return false;
}; // 对人的可达性经行判断,注意人不能走未移动时箱子的位置
// 定义剔除状态数组vis[x][y][dir]表示通过向dir移动来到(x, y)
// 表明状态在方向上单调,避免排序操作
std::vector< std::vector< std::vector< int > > > vis(m,
std::vector >(n, std::vector< int >(4, 0)));
std::vector > dp(m, vector(n, -1) );
dp[b.x][b.y] = 0;
queue que;
state now(b,s);
que.push(now);
Point people, move_dir;
while (!que.empty()) {
Point curr = que.front().box;
s = que.front().people;
que.pop();
if (curr == t) {
return dp[t.x][t.y];
}
for (int i = 0; i < 4; ++i) {
// 箱子移动后的位置
move_dir.x = curr.x + dir[i][0], move_dir.y = curr.y + dir[i][1];
// 人的推动位置
people.x = curr.x - dir[i][0], people.y = curr.y - dir[i][1];
// 推动位置和移动位置合法,状态首次更新,且推动位置可达
if (check(people) && check(move_dir) &&
!vis[move_dir.x][move_dir.y][i] && bfs(s, people, curr)) {
vis[move_dir.x][move_dir.y][i] = 1;
que.push(state(move_dir, curr));
dp[move_dir.x][move_dir.y] = dp[curr.x][curr.y] + 1;
}
}
}
return dp[t.x][t.y];
}
}; 引用资料
【最用心 の Unity百宝箱】A星寻路算法+迪杰斯特拉+广度优先寻路
《算法竞赛进阶指南》
在线OJ平台 -- leetcode