RSA攻击：Smooth攻击

目录

前言：缘起

P-1光滑攻击

P+1光滑攻击

    前缀知识

        Lucas-Subsquence(卢卡斯序列)

    编码实现与理解

小试牛刀

    [NCTF 2019]childRSA

    引用

---

前言：缘起

    Smooth攻击(光滑攻击)，在最近刷题的时候总是能偶尔蹦跶到我的脑子里面。不是天天遇见它，而是其背后的原理总是让人头痛。所以，为了解决心头大患，只好尽自己所能搜罗网上资料理解Smooth攻击背后的数学原理。特此来记录这几天克服中的重重险阻时，迸发的灵感。

    光滑攻击有两种：p-1光滑攻击，p+1光滑攻击。其中p-1光滑攻击是容易理解的，理解他并非什么难事。网上也不缺少它的证明，但是p+1光滑攻击则恰恰相反。首先，它违反人类感觉上的认知(编码上)，所以阅读代码解析时困难，其次理论知识需要一定储备，所以学习上成本较大。因此，本文会对前者做出证明和记录，对后者给出部分性质证明以及一些个人的理解。

    下面就进入正文啦~

---

P-1光滑攻击

    P-1光滑攻击的底层原理，比较符合我们的小学认知。我们先给出一些定义以及结论。

定义1：一个数n可以被分解为若干小质数的乘积，则称其为光滑数。

定义2：若一个光滑数最大的小质数因子 <= B, 则称其为 B-光滑数。

即 n = 。

    特此说明，定义2中的表达式解释中应当满足这条关系：。

    从上面的两个定义中，我们不难可以得出一个事实。如果光滑数N的小质数因子互不相同，那么有  。也就是说，。

    正是因为B-光滑数的这一特性，加上给出的条件是p-1为光滑数，我们可以很自然的联想到使用费马小定理来配合求解。

    以为下为p-1光滑数的证明：

    通过上述证明，我们明确了因此P的可计算性，一旦N，P，Q知其二，那么RSA就得以破解。剩下的计算过程想必大家都了如指掌，就不展开说了。

    上脚本

# 采用Python语言编写

imoprt gmpy2

def Pollards_p_1(N):
    a = 2 # 为了快速计算以及满足费马小定理条件
    n = 2 # 从1开始没必要
    
    while(True):
        a = pow(a, n, N) # 递推计算a^B!
        p = gmpy2.gcd(a - 1, N) # 尝试计算p
        if p != 1 and p != n: # 满足要求则返回
            return p
        n += 1
    

P+1光滑攻击

     在这种攻击方式下，底层的数学原理并非那么被人熟知或者被我们频繁使用。因此，我需要较大篇幅的导入一些前缀知识。如果你嫌弃篇幅过长的话，可以根据目录索引至代码部分的理解。

    前缀知识

        Lucas-Subsquence(卢卡斯序列)

            这个名字有些令人陌生，确实它不如它的“好兄弟”，Fiboncci，那般有名气。现在，我们直接给出卢卡斯序列的样子(在密码学应用中)，,于是，我们可以使用特征根将其求解。先将原式子变换为 ,得到两个根为。因此，等于。带入n = 1时，由待定系数法可知，λ = 1。

            接下来，我们需要找到卢卡斯序列的最小循环节。令s = 。

            注意：两个多项式出去首位两项，其他的偶数都是p的配属二次项系数决定了p已知存在。 

    编码实现与理解

      当然有了一些潦草的前缀知识之后，我们并不能马上解出答案。因为这需要我们对RSA原过程做出一些变换，以及扩展一些数学知识。

        引理1：对于卢卡斯序列，成立。

        引理可以通过通项式子证明，其次因为m，n位置可以到对调，所以我们不让m>n吧，这样序列就不有负下标。

        根据前缀知识，我们了解到，S(N)一定是数列的一个循环周期，但不一定是最小周期。但是这已经够了。

def lucas(c, d, N):
	x = c # a1
	y = (c**2 - 2) % N # a2
	for bit in bin(d)[3:]: # 快速乘(从高到低位)--我个人理解
		if bit == '1':
			x = (x*y - c) % N # 下标对应a_{x+y}，其次保证a_{2k-1}=a_{k}a_{k-1}-a_{0}成立
			y = (y**2 - 2) % N # 使得y翻倍--正常的快速幂流程
		else:
			y = (x*y - c) % N # 保证a_{2k-1}=a_{k}a_{k-1}-a_{0}成立
			x = (x**2 - 2) % N # a_{k} 翻倍
	return x #返回a_{ed}

        关于编码层面上采用快速乘的想法。源于引理1，由其可知，， ，且。所以计算小标ed时，我们可以把d拆分为2进制数，依次用来完成快速乘。

小试牛刀

    [NCTF 2019]childRSA

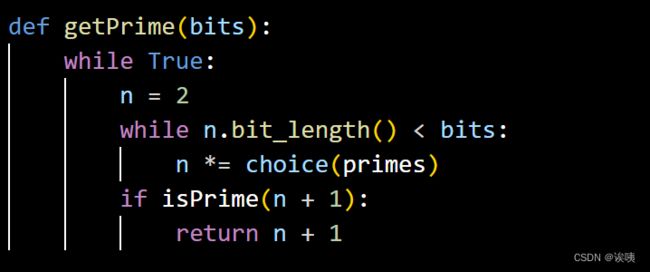
    获取附件之后，我们可以看到以下代码段。

    我们，容易分析出P、Q是自定义素数生成器生成的。因此，我们的重点核心来到解析素数生成器的原理。

    通过 n *= choice(primes) 知道，这一通过小素数累积得到的，并且这些小素数互不相同。除此之外，我们发现最后的返回值为 n + 1，也就是说 p = n + 1，即 p - 1 是一个光滑数。因此，我们可以选择p-1光滑攻击。

def Pollards_p_1(N):
    a = 2 # 为了快速计算以及满足费马小定理条件
    n = 2 # 从1开始没必要
    
    while(True):
        a = pow(a, n, N)
        p = gmpy2.gcd(a - 1, N)
        if p != 1 and p != n:
            return p
        n += 1

p = Pollards_p_1(n)

     由上诉代码段破解得到：

p = 178449493212694205742332078583256205058672290603652616240227340638730811945224947826121772642204629335108873832781921390308501763661154638696935732709724016546955977529088135995838497476350749621442719690722226913635772410880516639651363626821442456779009699333452616953193799328647446968707045304702547915799734431818800374360377292309248361548868909066895474518333089446581763425755389837072166970684877011663234978631869703859541876049132713490090720408351108387971577438951727337962368478059295446047962510687695047494480605473377173021467764495541590394732685140829152761532035790187269724703444386838656193674253139

# 因此
q = n // p
phi = (p - 1) * (q - 1)
import primefac
e = 0x10001
d = primefac.modinv(e, phi)
c = 26308018356739853895382240109968894175166731283702927002165268998773708335216338997058314157717147131083296551313334042509806229853341488461087009955203854253313827608275460592785607739091992591431080342664081962030557042784864074533380701014585315663218783130162376176094773010478159362434331787279303302718098735574605469803801873109982473258207444342330633191849040553550708886593340770753064322410889048135425025715982196600650740987076486540674090923181664281515197679745907830107684777248532278645343716263686014941081417914622724906314960249945105011301731247324601620886782967217339340393853616450077105125391982689986178342417223392217085276465471102737594719932347242482670320801063191869471318313514407997326350065187904154229557706351355052446027159972546737213451422978211055778164578782156428466626894026103053360431281644645515155471301826844754338802352846095293421718249819728205538534652212984831283642472071669494851823123552827380737798609829706225744376667082534026874483482483127491533474306552210039386256062116345785870668331513725792053302188276682550672663353937781055621860101624242216671635824311412793495965628876036344731733142759495348248970313655381407241457118743532311394697763283681852908564387282605279108
m = pow(c, d, n)
print(long_to_bytes(m))

    从而我们获取flag：NCTF{Th3r3_ar3_1ns3cure_RSA_m0duli_7hat_at_f1rst_gl4nce_appe4r_t0_be_s3cur3}

    引用

            1.Cryptosystem on lucas - hash_hash​​​​​

            2.Wiki