神经网络模型压缩技术—剪枝
目录
1.模型压缩定义
2.模型压缩必要性及可行性
3.模型压缩分类
3.1 主流分类
3.2 前端和后端
4.剪枝
4.1 剪枝定义
4.2 剪枝分类
4.2.1 基于粒度
4.2.2 基于是否结构化
4.2.3 基于目标
5. 结构化剪枝和非结构化剪枝
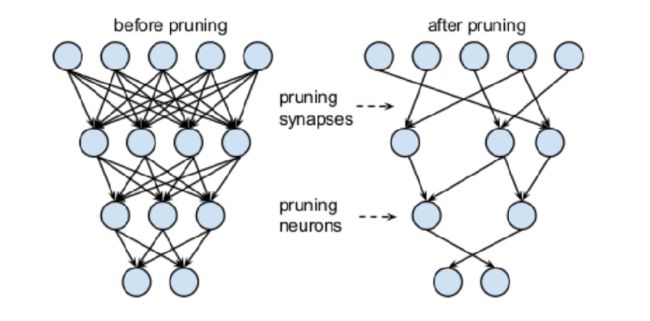
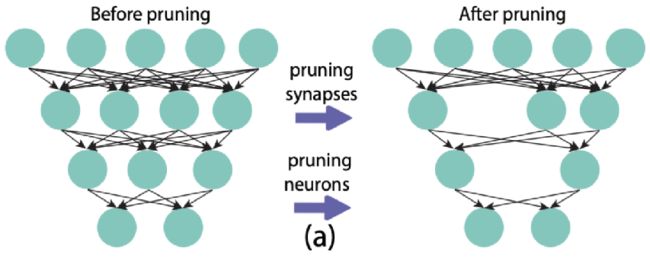
5.1 非结构化剪枝(移除单个权重或神经元)
5.2 结构化剪枝(移除一组规则的的权重,如过滤器剪枝、通道剪枝)
6 剪枝算法步骤
7 剪枝总结
1.模型压缩定义
利用神经网络参数的冗余性和网络结构的冗余性精简模型,在不影响任务完成度的情况下,得到参数量更少、结构更精简的模型。被压缩后的模型计算资源需求和内存需求更小,相比原始模型能够满足更加广泛的应用需求。
2.模型压缩必要性及可行性
(1)必要性:首先是模型需要部署在移动设备上,而这些移动设备往往存储空间和计算能力都相对受限,因此使用模型压缩可以有效降低模型参数量和计算量。其次在许多网络结构中,如VGG-16网络,参数数量1亿3千多万,占用500MB空间,需要进行309亿次浮点运算才能完成一次图像识别任务;
(2)可行性:模型的参数在一定程度上能够表达其复杂性,相关研究表明,并不是所有的参数都在模型中发挥作用,部分参数作用有限、表达冗余,甚至会降低模型的性能。相关论文提出,很多的深度神经网络仅仅使用很少一部分(5%)权值就足以预测剩余的权值。论文还提出这些剩下的权值甚至可以直接不用被学习。也就是说,仅仅训练一小部分原来的权值参数就有可能达到和原来网络相近甚至超过原来网络的性能;
(3)最终目的:最大程度的减小模型复杂度,减少模型存储需要的空间,也致力于加速模型的训练和推测。
3.模型压缩分类
3.1 主流分类
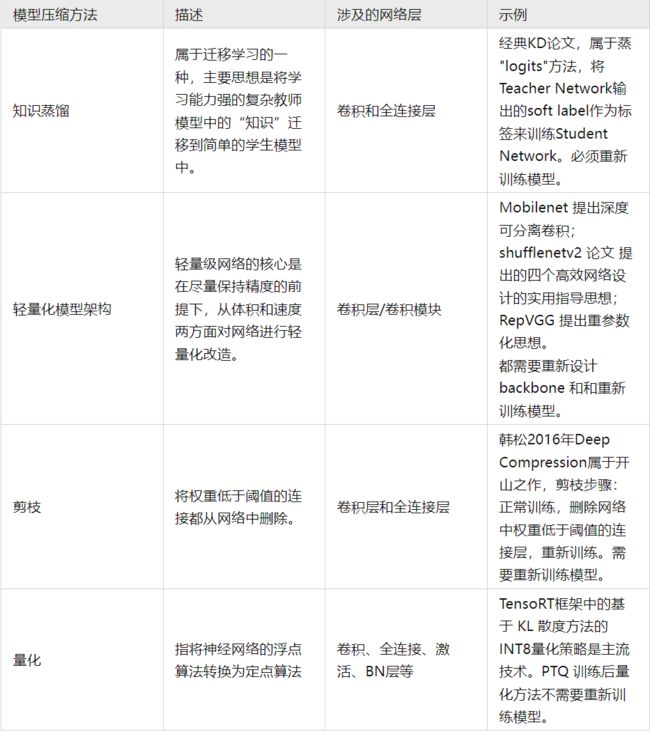
目前模型压缩方法主要分为五大类:剪枝(pruning)、量化(quantization)、知识蒸馏(knowledge distillation)、低秩近似(low-rank Approximation)和紧凑网络设计(compact Network design)。
3.2 前端和后端
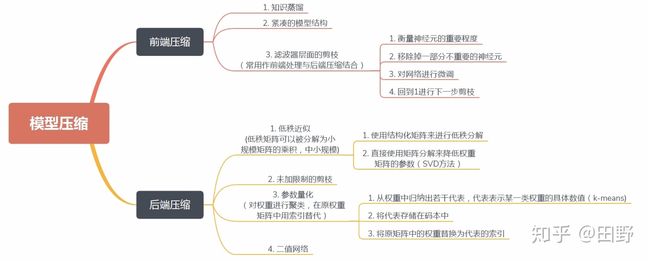
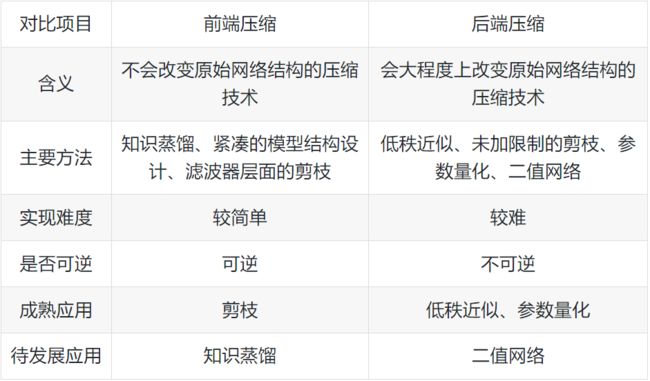
按照压缩过程对网络结构的破坏程度,《解析卷积神经网络》一书中将模型压缩技术分为“前端压缩”和“后端压缩”两部分:
- 前端压缩,是指在不改变原网络结构的压缩技术,主要包括知识蒸馏、轻量级网络(紧凑的模型结构设计)以及滤波器(filter)层面的剪枝(结构化剪枝)等;
- 后端压缩,是指包括低秩近似、未加限制的剪枝(非结构化剪枝/稀疏)、参数量化以及二值网络等,目标在于尽可能减少模型大小,会对原始网络结构造成极大程度的改造。
总结:前端压缩几乎不改变原有网络结构(仅仅只是在原模型基础上减少了网络的层数或者滤波器个数),后端压缩对网络结构有不可逆的大幅度改变,造成原有深度学习库、甚至硬件设备不兼容改变之后的网络。其维护成本很高。
4.剪枝
4.1 剪枝定义
剪枝方法探索模型权重中的冗余, 并尝试删除/修剪冗余和非关键的权重。
4.2 剪枝分类
4.2.1 基于粒度
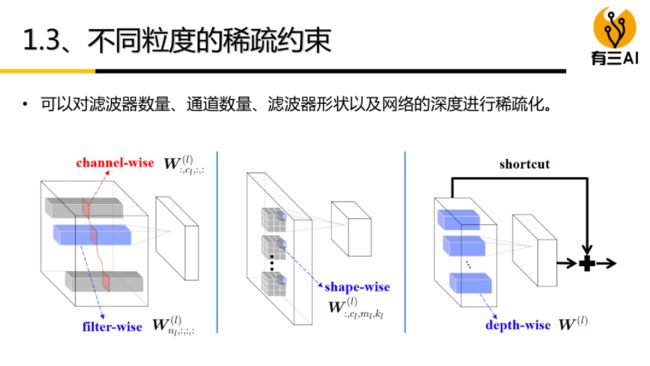
模型剪枝算法根据粒度的不同,可以粗分为4种粒度:
- 细粒度剪枝(fine-grained):对连接或者神经元进行剪枝,它是粒度最小的剪枝。
- 向量剪枝(vector-level):它相对于细粒度剪枝粒度更大,属于对卷积核内部(intra-kernel)的剪枝。
- 核剪枝(kernel-level):去除某个卷积核,它将丢弃对输入通道中对应计算通道的响应。
- 滤波器剪枝(Filter-level):对整个卷积核组进行剪枝,会造成推理过程中输出特征通道数的改变。
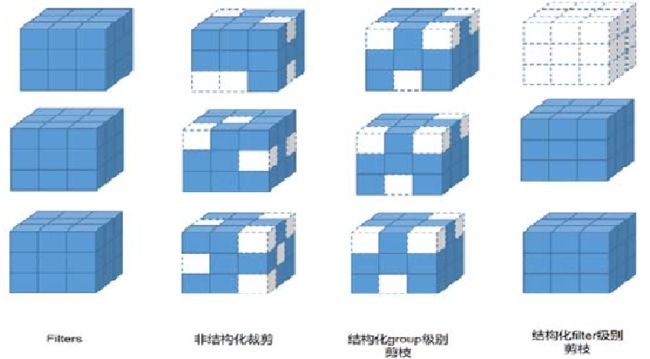
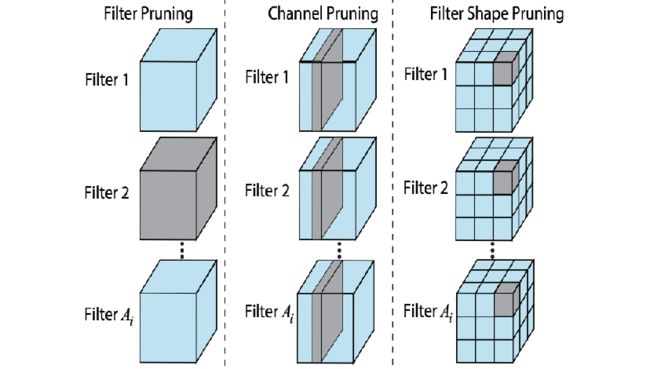
按剪枝粒度分,从粗到细,可分为中间隐含层剪枝、通道剪枝、卷积核剪枝、核内剪枝、单个权重剪枝。下面按照剪枝粒度的分类从粗(左)到细(右)。
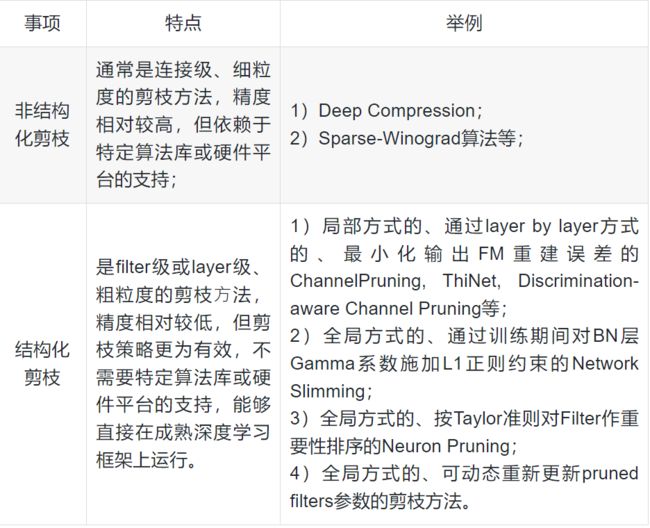
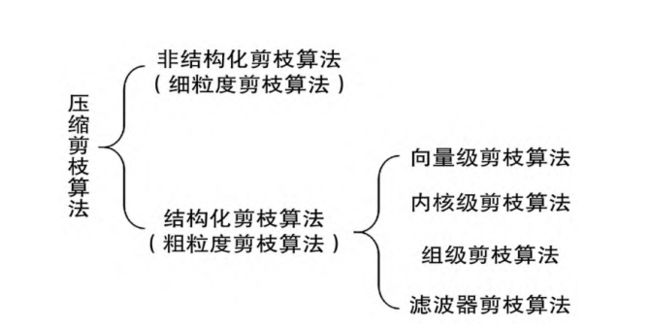
4.2.2 基于是否结构化
深度学习模型因其稀疏性,可以被裁剪为结构精简的网络模型,具体包括结构性剪枝与⾮结构性剪枝。
剪枝分为结构化剪枝和非结构化剪枝,两者区别在于是否会一次性删除整个节点或滤波器。
4.2.3 基于目标
从剪枝目标上分类,可分为减少参数/网络复杂度、减少过拟合/增加泛化能⼒/提高准确率、减⼩部署运行时间/提高网络效率及减小训练时间等。
5. 结构化剪枝和非结构化剪枝
5.1 非结构化剪枝(移除单个权重或神经元)
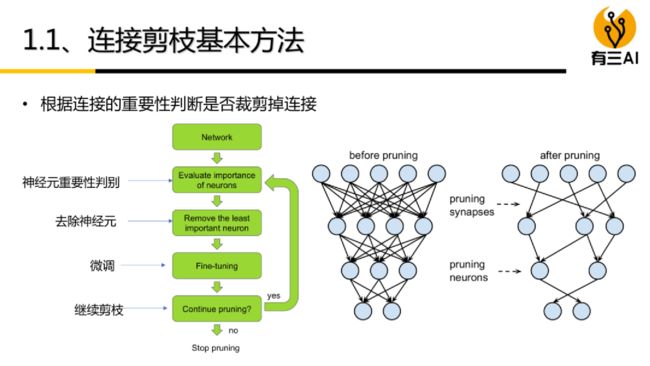
卷积层和全连接层的输入与输出之间都存在稠密的连接,对神经元之间的连接重要性设计评价准则,删除冗余连接,可达到模型压缩的目的。
根据神经元连接权值的范数值大小,删除范数值小于指定阈值的连接,可重新训练恢复性能。用突触强度来表示神经元之间连接的重要性。利用生物学上的神经突触概念,定义突触强度为 Batch Normalization(BN)层放缩因子 gamma和 filter 的 Frobinus 范数的乘积。在模型初始化阶段,通过对训练集多次采样判断连接的重要性,生成剪枝模板再进行训练,无需迭代进行剪枝-微调的过程。
5.2 结构化剪枝(移除一组规则的的权重,如过滤器剪枝、通道剪枝)
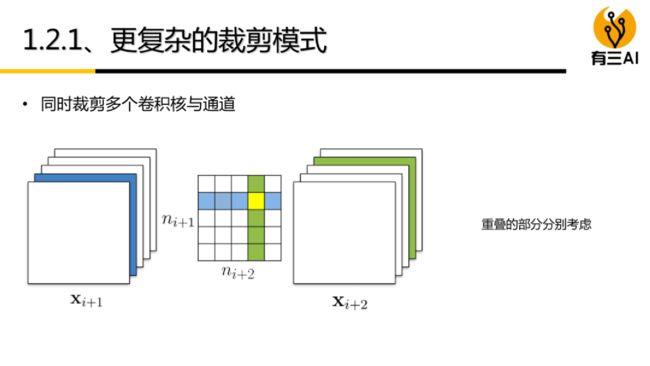
filter 级别剪枝也可以看作 channel 级别剪枝。如图所示,删去该层的某些 filter(即图中删去整个立方体),相当于删去其产生的部分 feature map 和原本需要与这部分 feature map 进行卷积运算的下一层部分 filter。
对 filter 的评价准则可分为以下4种:(1)基于 filter 范数大小 (2)自定义 filter 评分因子 (3)最小化重建误差 (4)其他方法。
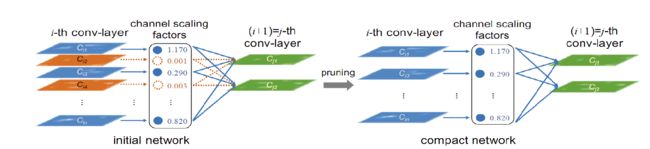
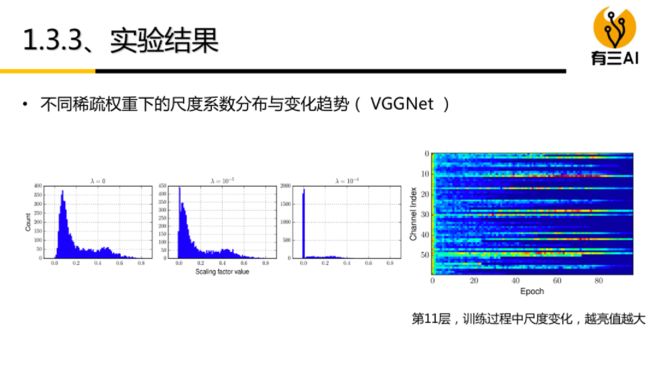
如下图所示,删除较小的通道缩放影子,达到模型压缩的目的。
6 剪枝算法步骤
- 正常训练模型;
- 模型剪枝;
- 重新训练模型。
以上三个步骤反复迭代进行,直到模型精度达到目标,则停止训练。