【Python 零基础入门】 Numpy

概述

在众多 Python 的数据处理库中, Numpy 是一个非常强大的存在. Numpy 为我们提供了高性能的多维数组, 以及这些数组对象上的各种操作. 但是, 作为一个刚入门 Python 的新手, 你可能会问: "为什么我需要 Numpy, 而不是直接使用Python 的内置列表?"在这篇文章的开篇, 我们就来探讨这个问题.

什么是 Numpy?

Numpy (Numerical Python) 是 Python 非常重要的一个库, 用于处理数值数组. Numpy 为我们提供了大量数据处理的函数以及数学函数. 与 Python 的内列表相比, Numpy 数组在数据分析, 科学计算, 线性代数, 机器学习等方面都表现出了卓越的性能和效率.

Numpy 与 Python 数组的区别

虽然 Python 的内置列表很灵活, 能存储任意类型的数据. 但当我们需要进行大量的数值运算时 (线性代数, 统计), Python 的内置列表效率并不高. Numpy 数组相比之下, 是在连续的内存块上存储的, 这使得访问速度更快, 效率更高. 而且 Numpy 是用 C 语言编写的, 其内部迭代计算比 Python 的内置循环要快很多.

例子:

并发 vs 并行

并发 vs 并行

• 并发 (Concurrency): 是指系统能够处理多个任务在同一时间段内交替执行, 但不一定同时
• 并行 (Parallelism): 并行是指多个任务或多个数据在同一时刻被执行

举个例子:

• 并发: 类似一个单线程的服务器, 可以在短时间内处理多个请求, 但是一次只能处理一个请求. 当等待一个请求数据时, 可以切换到另一个请求
• 并行: 想象成一个多线程的计算任务, 每个线程在多核 CPU 不同核心上同时执行

举个生活中的例子:

小白吃饭吃到一半, 电话来了, 我一直到吃完了以后才去接, 这就说明你不支持并发也不支持并行.
小白吃饭吃到一半, 电话来了, 你停了下来接了电话, 接完后继续吃饭, 这说明你支持并发.
小白吃饭吃到一半, 电话来了, 你一边听电话一边吃饭, 这说明你支持并行.

应用:

• 并发: 进行任务之间的协调 & 同步, 难点在有效地处理资源争用 & 死锁
• 并行: 同时进行多个任务, 难点在于负载均衡和通信开销

单线程 vs 多线程

单线程 vs 多线程:

• 单线程: 在同一时间处理一个任务
• 多线程: 在同一时间处理多个任务

GIL

GIL (Global Interpreter Lock) 全局解释器, 来源是 Python设计之初的考虑, 为了数据安全所做的决定.

每个 CPU 在同一时间只能执行一个线程 (在单核 CPU 下的多线程其实都只是并发, 不是并行, 并发和并行从宏观上来讲都是同时处理多路请求的概念. 但并发和并行又有区别, 并行是指两个或者多个事件在同一时刻发生, 而并发是指两个或多个事件在同一时间间隔内发生.

Numpy 在数据科学中的重要性

在现代数据科学领域, 数据处理, 清晰, 统计分析, 特征工厂, 机器学习等各个领域都离不开数值计算. Numpy 为我们提供了一套完整, 高效的工具, 使得我们的任务变得简单. 几乎所有的 Python 数据处理库, 如 Pandas, Scipy 等, 都是基于 Numpy 构建的. 所以我们非常有必要要熟悉掌握 Numpy 库.

Numpy 安装

安装命令:

pip install numpy
pip3 install numpy

Anaconda

Anaconda 是一个计算科学库, 可以为我们提供便利的 Python 环境.

安装:
Anaconda 官网

导包

导入 Numpy 包:

# 导包
import numpy as np


print(np.__version__)

ndarray

ndarray 是 Numpy 最重要的一个特点. ndarray 是一个 N 维数组对象.

np.array 创建

np.array可以帮助我们创建一 ndarray.

格式:

numpy.array(object, dtype=None, *, copy=True, order='K', subok=False, ndmin=0, like=None)

参数:

• object: 类数组
• dtype: 数据类型, 可选

例子:

# 导包
import numpy as np

# 创建ndarray
array1 = np.array([1, 2, 3])  # 通过lsit创建
array2 = np.array([1, 2, 3], dtype=float)

# 调试输出
print(array1, type(array1))
print(array2, type(array2))

输出结果:

[1 2 3] 
[1. 2. 3.] 

数组属性

创建 Numpy 数组后, 我们可以进一步查询 ndarray 的属性, 如形状, 维度, 数据类型等:

• shape: 返回数组的形状
• dtype: 返回数组中元素的数据类型
• ndim: 返回数组的维度
• size: 返回数组的元素总数

例子:

"""
@Module Name: Numpy 数组属性.py
@Author: CSDN@我是小白呀
@Date: October 13, 2023

Description:
Numpy 数组属性
"""

import numpy as np


# 创建 ndarray
arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr)

# 输出数组属性
print(arr.shape)  # 输出 [2, 3] (两行, 三列)
print(arr.dtype)  # 输出 int32 (整型)
print(arr.ndim)  # 输出 2 (二维数组)
print(arr.size)  # 输出 6 (2*3, 6个元素)

np.zeros 创建

np.zeros可以帮助我们创建指定形状的全 0 数组.

格式:

numpy.zeros(shape, dtype=float, order='C', *, like=None)

参数:

• shape: 数组形状
• detype: 默认为 float, 浮点型

例子:

import numpy as np

# 创建全0的ndarray
array = np.zeros((3, 3), dtype=int)
print(array)

输出结果:

[[0 0 0]
 [0 0 0]
 [0 0 0]]

np.ones 创建

np.zeros可以帮助我们创建指定形状的全 1 数组.

格式:

numpy.ones(shape, dtype=float, order='C', *, like=None)

参数:

• shape: 数组形状
• detype: 默认为 float, 浮点型

例子:

import numpy as np

# 创建全1的ndarray
array = np.ones((3, 3), dtype=int)
print(array)
print(type(array))

输出结果:

[[1 1 1]
 [1 1 1]
 [1 1 1]]

数组的切片和索引

Numpy 数组支持 Python 的索引和切片操作, 并提供了更为丰富的功能.

格式 1:

数组[起始索引:结束索引]

• 起始索引: 取的到
• 结束索引: 取不到

格式 2:

数组[起始索引:结束索引:间隔]

• 起始索引: 取的到
• 结束索引: 取不到
• 间隔: 间隔几个数

基本索引

import numpy as np


# 创建 ndarray
arr = np.array([1, 2 ,3 ,4 ,5])

# 切片, 取索引 0 对应的元素
print("输出第一个元素:", arr[0])  

输出结果:

输出第一个元素: 1

切片操作

例子:

import numpy as np


# 创建 ndarray
arr = np.array([1, 2 ,3 ,4 ,5])

# 切片数组前三个元素
print("前三个素:", arr[:3])

# 切片数组 2-3
print("2-3 元素:", arr[1:3])

# 切片最后一个元素
print("最后一个元素:", arr[-1])

# 切片奇数索引
print("奇数元素:", arr[::2])

# 切片反转
print("反转数组:", arr[::-1])

输出结果:

前三个素: [1 2 3]
2-3 元素: [2 3]
最后一个元素: 5
奇数元素: [1 3 5]
反转数组: [5 4 3 2 1]

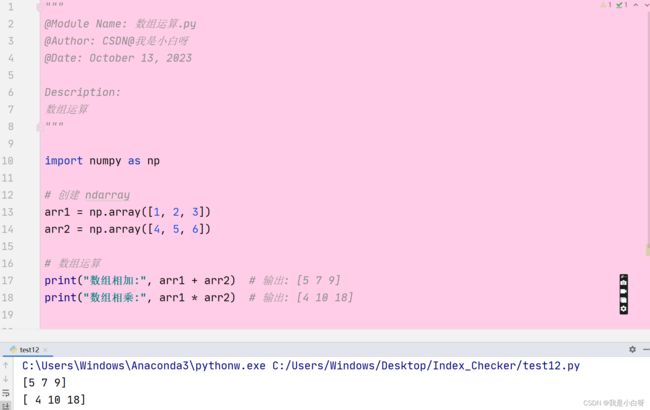
数组运算

与 Python 的内置列表不同, Numpy 数组支持元素级别的运算. 我们可以对 ndarray 进行加, 减, 乘, 除等操作.

例子:

常用函数

reshape

通过reshape()我们可以改变数组形状.

格式:

numpy.reshape(arr, newshape, order='C')

参数:

• arr: 需要改变形状的数组
• newshape: 新的形状

例子:

import numpy as np

# 创建ndarray
array = np.zeros(9)
print(array)

# reshape
array = array.reshape((3,3))
print(array)
print(array.shape)  # 调试输出数组形状

输出结果:

[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]
(3, 3) 

flatten

通过flatten()我们可以将多维数组摊平成1 维数组.

例子:

import numpy as np

# 创建多维数组
array = np.zeros((3, 3))
print(array)

# flatten转变为一维数组
array = array.flatten()
print(array)

输出结果:

[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]

聚合函数

常见的聚合函数:

• np.sum(): 求和
• np.min(): 求最小值
• np.max(): 求最大值
• np.mean(): 计算平均值
• np.median(): 计算中位数

例子:

import numpy as np


# 创建 ndarray
arr = np.array([1, 2, 3, 4, 5])

# 调用常用聚合函数
print(np.sum(arr))
print(np.min(arr))
print(np.max(arr))
print(np.mean(arr))
print(np.median(arr))

输出结果:

15
1
5
3.0
3.0

Numpy 的高级功能

下面我们来讲一下 Numpy 的高级功能. Numpy 的高级功能可以帮助我们有效的处理数据, 进行科学计算, 以便帮我们更好地处理数据.

广播

广播 (Broadcasting) 是 Numpy 的一个强大功能, 可以帮助我们进行不同形状数组的的运算. Numpy 中广播的规则是从尾部的维度开始对比.

例子:

import numpy as np

# 广播
a = np.array([1, 2, 3])
b = np.array([[10], [20], [30]])
print(a + b)

输出结果:

[[11 12 13]
 [21 22 23]
 [31 32 33]]

矩阵计算

例子:

import numpy as np


# 定义矩阵
mat1 = np.array([[1, 2], [3, 4]])
mat2 = np.array([[2, 0], [1, 3]])

# 矩阵乘法
# 1*2 + 2*1 = 2 
# 1*1 + 2*3 = 6
# 3*2 + 4*1 = 10
# 3*0 + 4*3 = 12
result = np.dot(mat1, mat2) 
print(result)

输出结果:

[[ 4  6]
 [10 12]]

Numpy 实际应用

当我们已经掌握了 Numpy 的基础用法和高级功能后, 小白我来带大家了解一下 Numpy 的实际应用.

统计分析

求数组平均数和标准差:

import numpy as np


# 定义数组
data = np.array([23, 45, 56, 78, 12, 9])

# 计算平均值和标准差
print("平均值:", np.mean(data))
print("标准差:", np.std(data))

输出结果:

3.14

图像处理

利用 Numpy, 我们可以将图像转化为数组进行处理.

例子:

import numpy as np
from PIL import Image

# 将图像转化为数据
image = Image.open('path_to_image.jpg')
image_array = np.array(image)
print(image_array.shape)

输出结果:

(1707, 2560, 3)

解方程

例子:

import numpy as np
from numpy.linalg import solve


# 创建 ndarray
a = np.array([[3, 1], [1, 2]])  # 3x + y = 9 
b = np.array([9, 8])  # x + 2y = 8

# 解方程
x = solve(a, b)  # x = 2, y = 3
print(x)

输出结果:

[2. 3.]

结论

在本篇文章中, 我们深入地探讨了 Numpy, 这是 Python 中用于数值计算和数据分析的核心库. 从数组的基本操作, 数组的形状和维度, 高级数组操作, 到 Numpy 的最佳实践和常见误区, 我们尝试为读者提供了一个全面且深入的视角.

Numpy 的真正威力在于其高效性和灵活性. 它为我们提供了大量的功能, 能帮助我们轻松处理大规模的数值数据. 但与此同时, 也需要注意其特定的工作原理, 避免常见的陷阱.

对于初学者来说, 可能需要一些时间来适应 Numpy 的思维方式, 特别是它的广播机制和向量化操作. 但一旦你习惯了这种方式, 你会发现自己的数据处理能力大大增强.

无论你是数据分析师, 科学家还是工程师, 掌握 Numpy 都将是你数据处理技能的重要组成部分. 希望这篇文章能为你在 Python 数据处理之路上提供一些有用的指导.

练习

练习1

数组创建与基础操作：

• 创建一个形状为 (5, 5) 的数组，其中所有元素都为整数1。
• 创建一个长度为 20 的一维随机整数数组，范围在 1 到 100 之间。
• 将上述一维数组重新塑形为 (5, 4) 的二维数组。

练习2

数组索引与切片：

• 创建一个形状为 (10, 10) 的随机整数数组，范围在 1 到 100 之间。提取出其中的第 3 到 8 行，第 4 到 9 列的子数组。
• 从上述数组中，提取出所有的偶数元素。

练习3

数组操作与数学运算：

• 创建两个形状为 (3, 3) 的随机整数数组 A 和 B，范围在 1 到 10 之间。计算 A 与 B 的点积。
• 计算上述数组 A 的逆矩阵（如果存在）。

参考答案

练习1

import numpy as np


array = np.ones([5,5], dtype=int)
print(array)
array = np.random.randint(1, 101, size=20)
print(array)
array = array.reshape((5, 4))
print(array)

输出结果:

[[1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]]
[22 13 20 67  5 91 26 64 84 85 59 66 44 83 41 63 44 23 76 35]
[[22 13 20 67]
 [ 5 91 26 64]
 [84 85 59 66]
 [44 83 41 63]
 [44 23 76 35]]

练习2

import numpy as np


array = np.random.randint(1, 101, size=(10, 10)).reshape((10,10))
print(array)
array = array[2:8, 3:9]
print(array)
array = array[array % 2 == 0]
print(array)

输出结果:

[[1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]]
[ 32   6  91  48  63  81  87  28  19  25  20  93  97 100  70  77   3  46
 100   7]
[[ 32   6  91  48]
 [ 63  81  87  28]
 [ 19  25  20  93]
 [ 97 100  70  77]
 [  3  46 100   7]]
[[1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]]
[71 63  6 50 59 69 14 18 80 88 68 54 35 97 51 82 86 50 61  9]
[[71 63  6 50]
 [59 69 14 18]
 [80 88 68 54]
 [35 97 51 82]
 [86 50 61  9]]

练习3

import numpy as np


a = np.random.randint(1, 11, size=(3, 3))
b = np.random.randint(1, 11, size=(3, 3))
print(a)
print(b)
result = np.dot(a, b)
print(result)

det_a = np.linalg.det(a)

if det_a == 0:
    print("矩阵 A 不可逆")
else:
    inverse_a = np.linalg.inv(a)
    print("A 的逆矩阵为: \n", inverse_a)

输出结果:

[[ 8  6  4]
 [10  5  5]
 [ 7  7  9]]
[[ 7  2  9]
 [10  9  6]
 [ 5  7  1]]
[[136  98 112]
 [145 100 125]
 [164 140 114]]
A 的逆矩阵为: 
 [[-9.09090909e-02  2.36363636e-01 -9.09090909e-02]
 [ 5.00000000e-01 -4.00000000e-01 -7.93016446e-18]
 [-3.18181818e-01  1.27272727e-01  1.81818182e-01]]