代码随想录算法训练营第一天|数组part01|704.35.34.27
2023/7/26 任务
数组理论基础,704. 二分查找,27. 移除元素
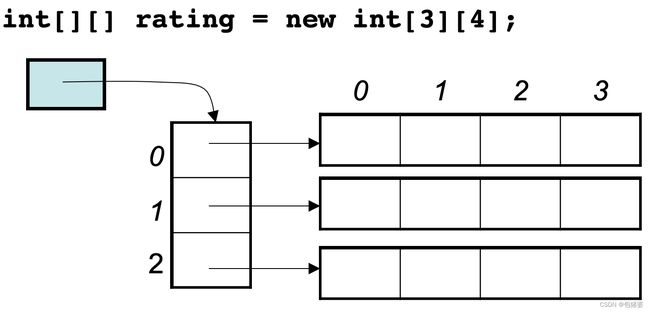
数组理论基础
704.二分查找 ⭐
左闭右闭/左闭右开
题目链接
文章讲解
视频讲解
二分法前提条件:
数组为有序数组
数组中无重复元素
易混点:
是right = nums.length - 1呢,还是right = nums.length,是 while(left < right) 还是 while(left <= right),是right = middle呢,还是right = middle - 1?
在循环中要坚持根据查找区间的定义(不变量)来做边界处理
注意辨别两种的区别
(版本一)左闭右闭区间 [left, right]
class Solution {
public int search(int[] nums, int target) {
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid - 1;
}
return -1;
}
}
时间复杂度:O(log n)
空间复杂度:O(1)
(版本二)左闭右开区间 [left, right)
- right = nums.length
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid;
}
return -1;
}
}
时间复杂度:O(log n)
空间复杂度:O(1)
相关题目
35.搜索插入位置
暴力/二分法
题目链接
文章讲解
(解法一)暴力法
class Solution {
public int searchInsert(int[] nums, int target) {
int i = 0;
for (; i < nums.length; i++) {
if (nums[i] >= target) {
break;
}
}
return i;
}
}
时间复杂度:O(n)
空间复杂度:O(1)
(解法二)二分法
相比704题,只有最后一行代码不同。
class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
}
}
return right + 1;
}
}
时间复杂度:O(log n)
空间复杂度:O(1)
34.在排序数组中查找元素的第一个和最后一个位置 ⭐
题目链接
文章讲解
寻找target在数组里的左右边界,有如下三种情况:
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
(解法一)
两个二分,分别寻找左右边界。
注意:计算出来的右边界是不包含target的右边界,左边界同理。
class Solution {
public int[] searchRange(int[] nums, int target) {
int rightBorder = searchRightBorder(nums, target);
int leftBorder = searchLeftBorder(nums, target);
// 情况一
if (leftBorder == -2 || rightBorder == -2) {
return new int[]{-1, -1};
}
// 情况三
else if (rightBorder - leftBorder > 1) {
return new int[]{leftBorder + 1, rightBorder - 1};
}
// 情况二
return new int[]{-1, -1};
}
public int searchRightBorder(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int rightBorder = -2;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
rightBorder = left;
}
}
return rightBorder;
}
public int searchLeftBorder(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int leftBorder = -2;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
leftBorder = right;
}
}
return leftBorder;
}
}
(解法二)
// 1、首先,在 nums 数组中二分查找 target;
// 2、如果二分查找失败,则 binarySearch 返回 -1,表明 nums 中没有 target。此时,searchRange 直接返回 {-1, -1};
// 3、如果二分查找成功,则 binarySearch 返回 nums 中值为 target 的一个下标。然后,通过左右滑动指针,来找到符合题意的区间
class Solution {
public int[] searchRange(int[] nums, int target) {
int index = binarySearch(nums, target); // 二分查找
if (index == -1) { // nums 中不存在 target,直接返回 {-1, -1}
return new int[] {-1, -1}; // 匿名数组
}
// nums 中存在 targe,则左右滑动指针,来找到符合题意的区间
int left = index;
int right = index;
// 向左滑动,找左边界
while (left - 1 >= 0 && nums[left - 1] == target) { // 防止数组越界。逻辑短路,两个条件顺序不能换
left--;
}
// 向右滑动,找右边界
while (right + 1 < nums.length && nums[right + 1] == target) { // 防止数组越界。
right++;
}
return new int[] {left, right};
}
/**
* 二分查找
*/
public int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 不变量:左闭右闭区间
while (left <= right) { // 不变量:左闭右闭区间
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1; // 不变量:左闭右闭区间
}
}
return -1; // 不存在
}
}
27. 移除元素 ⭐
暴力/双指针法
题目链接
文章讲解
视频讲解
(解法一)暴力解法
两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
class Solution {
public int removeElement(int[] nums, int val) {
int len = nums.length;
for (int i = 0; i < len; i++) {
if (nums[i] == val) {
for (int j = i; j < len - 1; j++) {
nums[j] = nums[j + 1];
}
i--;
len--;
}
}
return len;
}
}
时间复杂度:O(n^2)
空间复杂度:O(1)
(解法二)双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
慢指针:指向更新 新数组下标的位置
public int removeElement(int[] nums, int val) {
int slow = 0;
for (int fast = 0; fast < nums.length; fast++) {
if (nums[fast] != val) {
nums[slow++] = nums[fast];
}
}
return slow;
}
时间复杂度:O(n)
空间复杂度:O(1)