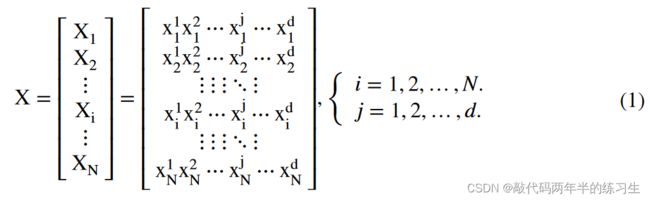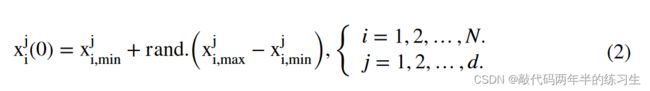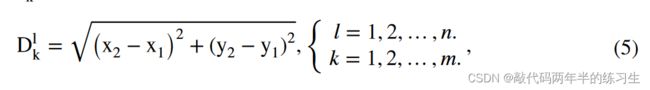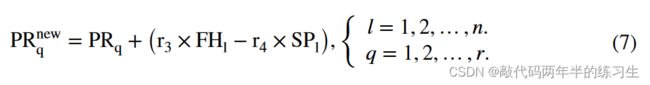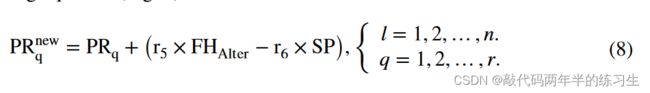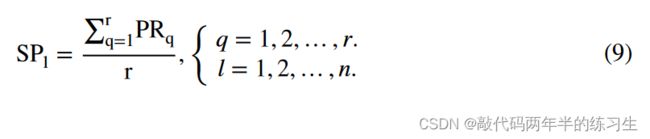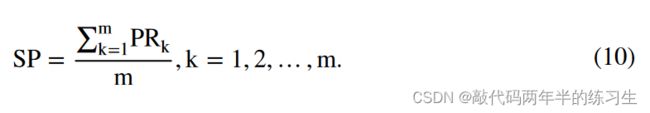【Matlab】智能优化算法_火鹰优化算法FHO
【Matlab】智能优化算法_火鹰优化算法FHO
- 1.背景介绍
- 2.数学模型
- 3.算法流程图
- 4.文件结构
- 5.伪代码
- 6.详细代码及注释
-
- 6.1 FHO.m
- 6.2 func_plot.m
- 6.3 Get_Functions_details.m
- 6.4 main.m
- 7.运行结果
- 8.参考文献
1.背景介绍
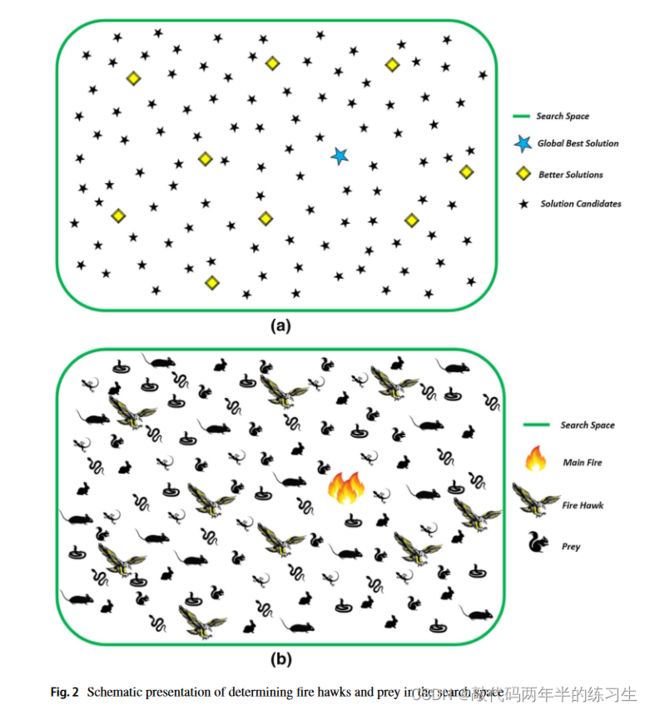
澳大利亚原住民利用火灾作为控制和维持当地生态系统和景观平衡的有效工具，多年来，这一直是文化和种族传统的一部分。大多数时候，故意引发或可能因闪电而自然发生的火灾可能由人和其他因素传播，增加了当地景观和野生动物的脆弱性。此外，吹口哨的风筝、黑风筝和棕色猎鹰也是在全国范围内传播火灾的原因——这一替代原因最近才被发现。这些被称为火鹰的鸟类试图通过喙和爪中携带燃烧的棍子来故意传播火灾，据报道，这是自然界中的一种破坏性现象。图1显示了这些鸟在火灾周围的行为。
作为控制和捕获猎物的一种机制，这些鸟会捡起燃烧的棍子，把它们扔到其他未燃烧的地方，以便生火。这些小火吓坏了猎物，包括啮齿动物、蛇和其他动物，迫使它们以最匆忙和紧张的方式逃跑，这使得鹰更容易捕捉。
2.数学模型
FHO元启发式算法模拟了火鹰的觅食行为，考虑了生火、生火和捕捉猎物的过程。首先，确定多个候选解（X）作为火鹰和猎物的位置向量。利用随机初始化过程来识别这些向量在搜索空间中的初始位置。
其中，Xi表示搜索空间中的第i个候选解决方案；d表示所考虑问题的维度；N是搜索空间中候选解决方案的总数；xj-i是第i个候选解的第j个决策变量；xj i（0）表示候选解决方案的初始位置；xji，min和xj i，max是第i个候选解的第j个决策变量的最小界和最大界；rand是[0,1]范围内的均匀分布随机数。
为了确定火鹰在搜索空间中的位置，候选解的目标函数评估考虑了所选的优化问题。一些目标函数值较好的候选解被表示为火鹰，而其余的候选解则是猎物。选定的火鹰用于在搜索空间中向猎物周围生火，以使狩猎更容易。此外，全局最佳解决方案被假设为火鹰首先利用的主要火灾，以通过搜索空间（自然）传播火灾。在图2a，b中，提供了这些方面的示意图，其数学表示如下：
其中PRk是关于m只猎物的总数的搜索空间中的第k只猎物；考虑到搜索空间中总共有n只火鹰，FHl是第l只火鹰。
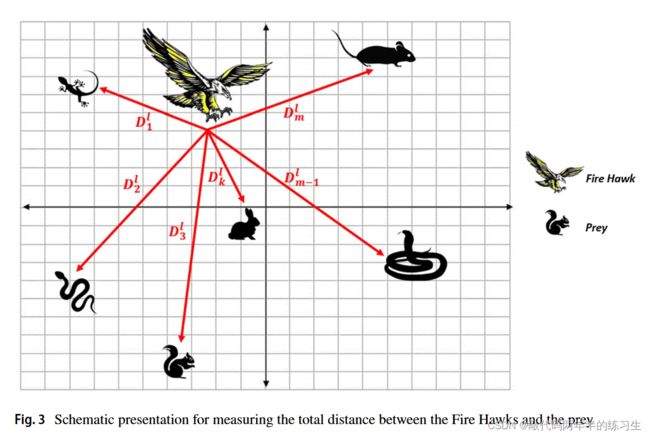
在算法的下一阶段，计算火鹰和猎物之间的总距离。因此，确定了离每只鸟最近的猎物，从而区分了这些鸟的有效领地。需要注意的是，以最佳目标函数值确定距离第一只火鹰最近的猎物，而通过剩余的猎物来考虑其他鸟类的领地。图3说明了这一观点，其中Dl k通过以下方程确定：
其中，Dl k是第1只火鹰和第k只猎物之间的总距离；m是搜索空间中猎物的总数；n是搜索空间中的火鹰总数；（x1，y1）和（x2，y2）表示火鹰和猎物在搜索空间中的坐标。
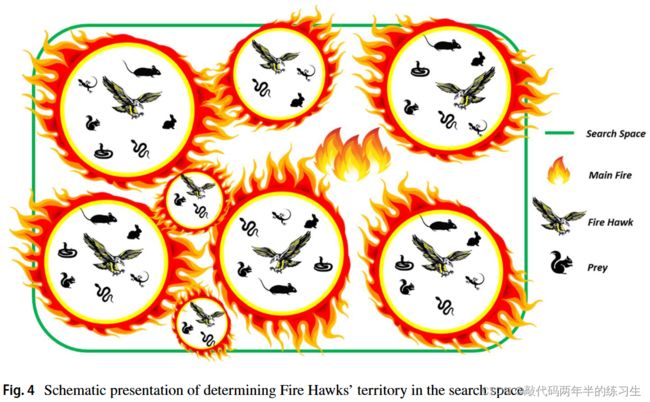
在进行了上述测量火鹰和猎物之间总距离的程序后，通过它们周围最近的猎物来区分这些鸟的领地。通过对火鹰和猎物进行分类，配置了算法的搜索过程。需要注意的是，目标函数值较好的火鹰会为其特定领地选择搜索空间中距离最近的最佳猎物。然后，其他火鹰在搜索空间中完成下一个最近的猎物，这支持了最强的火鹰比较弱的鸟更成功地完成狩猎。在图4中，提供了在搜索空间中确定火鹰领地的示意图。
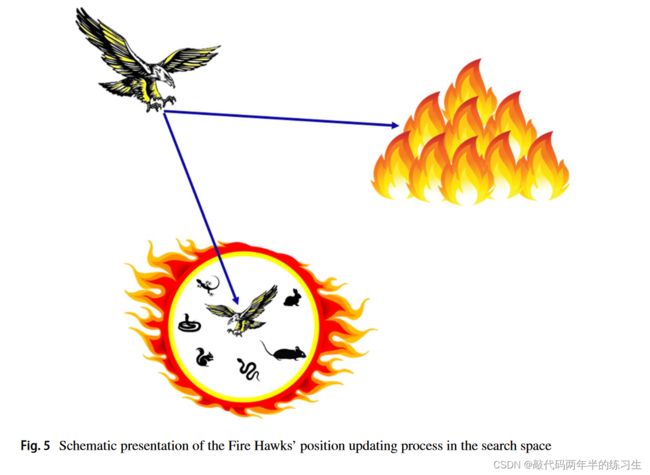
在算法的下一阶段，火鹰从主火中收集燃烧的棍子，以便在选定区域点火。在这个阶段，每只鸟都会拿起一根燃烧的棍子，然后把它扔到自己的特定区域，迫使猎物匆忙逃离。与此同时，一些鸟类渴望使用来自其他火鹰领地的燃烧棒；因此，这两种行为可以用作FHO主搜索循环中的位置更新过程，如以下等式所示：
其中FHnew l是第l个火鹰（FHl）的新位置矢量；GB是全球最佳的搜索解决方案，被认为是主要的火灾；FHNear是搜索空间中的其他火鹰之一；r1和r2是在（0，1）范围内均匀分布的随机数，用于确定火鹰向主火和其他火鹰领地的移动（见图5）。
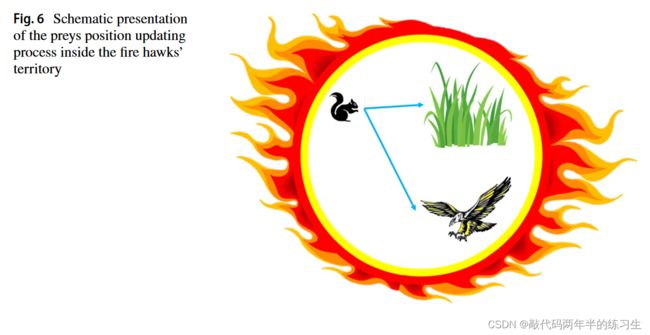
在算法的下一阶段，猎物在每只火鹰领地内的移动被认为是位置更新过程中动物行为的一个关键方面。当一根燃烧的棍子被火鹰扔下时，猎物决定躲藏、逃跑，或者会错误地跑向火鹰。在位置更新过程中，可以通过使用以下等式来考虑这些动作：
其中PRnew q是第q个猎物（PRq）的新位置矢量，该第q个被第l个火鹰（FHl）包围；GB是全球最佳的搜索解决方案，被认为是主要的火灾；SPl是第三火鹰领地下的一个安全地点；r3和r4是（0，1）范围内的均匀分布随机数，用于确定猎物向火鹰和安全地点的移动（见图6）。
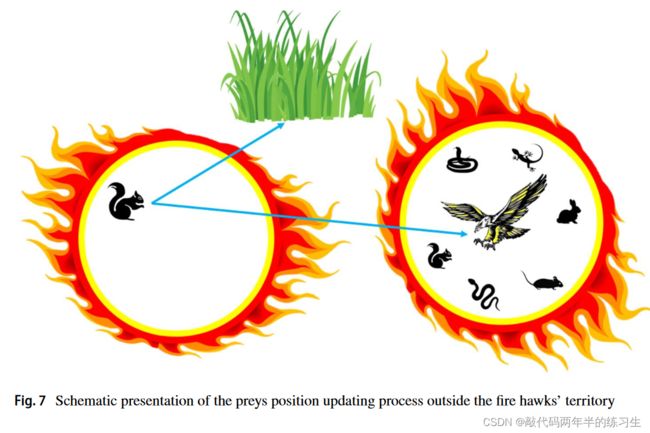
此外，猎物可能会向其他火鹰的领地移动，而猎物可能会在近距离伏击中靠近火鹰，甚至试图躲在火鹰领地外更安全的地方。在位置更新过程中，可以使用以下等式来考虑这些动作（图7）：
其中PRnew q是第q个猎物（PRq）的新位置矢量，该第q个被第lthfire hawk（FHl）包围；FHAlter是搜索空间中的其他火鹰之一；SP是第三火鹰领地以外的安全地点；r5和r6是在（0，1）范围内均匀分布的随机数，用于确定猎物向其他火鹰和领地外安全地点的移动。
基于自然界中的安全场所是大多数动物为了在危险期间保持安全和健康而聚集的地方这一事实，SPl和SP的数学表示公式如下：
其中PRq是被第1只火鹰（FHl）包围的第q只猎物；PRk是搜索空间中的第k个猎物。
需要注意的是，出于示意图的目的，每只火鹰的领地都被假设为圆形区域，因此领地的确切定义取决于猎物和所考虑的火鹰的总体距离。换言之，当猎物位于特定的火鹰领地时，假设它受到所考虑的火鹰而不是其他火鹰的影响，因此猎物的数量及其与所考虑的火鹰的距离决定了这只火鹰领地的限制。同时，在位置更新过程中，也考虑了猎物在自己领土之外的可能性，因为猎物应该受到来自其他领土的火鹰的影响。每个搜索循环中的猎物数量是候选解决方案的总数减去通过布朗运动随机确定的火鹰数量，其中高斯分布是rand中使用的众所周知的分布之一。
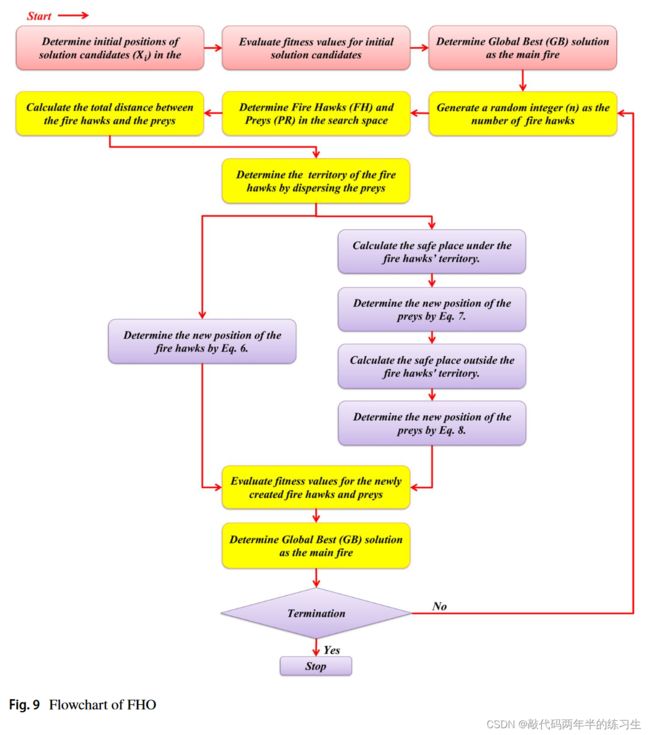
3.算法流程图
4.文件结构
FHO.m % 火鹰优化算法
func_plot.m % 绘制的基准函数
Get_Functions_details.m % 基准的全部信息和实现
main.m % 主函数
5.伪代码
6.详细代码及注释
6.1 FHO.m
%% Fire Hawk Optimizer (FHO) source code - version 1.0
% Programmer: Mahdi Azizi, Siamak TalatAhari, Amir H. Gandomi
% E-mail: mehdi.azizi875@gmail.com
% Main source:
% Fire Hawk Optimizer: a novel metaheuristic algorithm
% https://link.springer.com/article/10.1007/s10462-022-10173-w
%% Clear Workspace & Command Window
function [GB, Best_Pos,Conv_History ] = FHO(nPop, MaxFes,lb,ub,dim,CostFunction )
%% Problem Information
VarMin = lb *ones(1,dim); % Lower bound of variable;
VarMax = ub *ones(1,dim); % Upper bound of variable;
%% General Parameters of the Algorithm
HN = randi([1 ceil(nPop/5)],1,1) ; % Maximum number of FireHawks
% Counters
Iter=0;
FEs=0;
%% Initialization
Pop=[]; Cost=[];
for i=1:nPop
% Initialize Positions
Pop(i,:)=unifrnd(VarMin,VarMax,[1 dim]);
% Cost Function Evaluations
Cost(i,1)=CostFunction(Pop(i,:));
FEs=FEs+1;
end
% Sort Population
[Cost, SortOrder]=sort(Cost);
Pop=Pop(SortOrder,:);
BestPop=Pop(1,:);
SP=mean(Pop);
% Fire Hawks
FHPops=Pop(1:HN,:);
% Prey
Pop2=Pop(HN+1:end,:);
% Distance between Fire Hawks and Prey
for i=1:HN
nPop2=size(Pop2,1);
if nPop2<HN
break
end
Dist=[];
for q=1:nPop2
Dist(q,1)=distance(FHPops(i,:), Pop2(q,:));
end
[ ~, b]=sort(Dist);
alfa=randi(nPop2);
PopNew{i,:}=Pop2(b(1:alfa),:);
Pop2(b(1:alfa),:)=[];
if isempty(Pop2)==1
break
end
end
if isempty(Pop2)==0
PopNew{end,:}=[PopNew{end,:} ;Pop2];
end
% Update Bests
GB=Cost(1);
BestPos=BestPop;
%% Main Loop
for FEs=1:MaxFes
Iter=Iter+1;
PopTot=[];
Cost=[];
for i=1:size(PopNew,1)
PR=cell2mat(PopNew(i));
FHl=FHPops(i,:);
SPl=mean(PR);
Ir=unifrnd(0,1,1,2);
FHnear=FHPops(randi(HN),:);
FHl_new=FHl+(Ir(1)*GB-Ir(2)*FHnear);
FHl_new = max(FHl_new,VarMin);
FHl_new = min(FHl_new,VarMax);
PopTot=[PopTot ;FHl_new];
for q=1:size(PR,1)
Ir=unifrnd(0,1,1,2);
PRq_new1=PR(q,:)+((Ir(1)*FHl-Ir(2)*SPl));
PRq_new1 = max(PRq_new1,VarMin);
PRq_new1 = min(PRq_new1,VarMax);
PopTot=[PopTot ;PRq_new1];
Ir=unifrnd(0,1,1,2);
FHAlter=FHPops(randi(HN),:);
PRq_new2=PR(q,:)+((Ir(1)*FHAlter-Ir(2)*SP));
PRq_new2 = max(PRq_new2,VarMin);
PRq_new2 = min(PRq_new2,VarMax);
PopTot=[PopTot ;PRq_new2];
end
end
for i=1:size(PopTot,1)
Cost(i,1)=CostFunction(PopTot(i,:));
FEs=FEs+1;
end
% Sort Population
[Cost, SortOrder]=sort(Cost);
PopTot=PopTot(SortOrder,:);
Pop=PopTot(1:nPop,:);
HN = randi([1 ceil(nPop/5)],1,1);
BestPop=Pop(1,:);
SP=mean(Pop);
FHPops=Pop(1:HN,:);
Pop2=Pop(HN+1:end,:);
clear PopNew
% Distance between Fire Hawks and Prey
for i=1:HN
nPop2=size(Pop2,1);
if nPop2<HN
break
end
Dist=[];
for q=1:nPop2
Dist(q,1)=distance(FHPops(i,:), Pop2(q,:));
end
[ ~, b]=sort(Dist);
alfa=randi(nPop2);
PopNew{i,:}=Pop2(b(1:alfa),:);
Pop2(b(1:alfa),:)=[];
if isempty(Pop2)==1
break
end
end
if isempty(Pop2)==0
PopNew{end,:}=[PopNew{end,:} ;Pop2];
end
% Update Bests
if Cost(1)<GB
BestPos=BestPop;
end
GB=min(GB,Cost(1));
% Store Best Cost Ever Found
BestCosts(Iter)=GB;
% Show Iteration Information
% disp(['Iteration ' num2str(Iter) ': Best Cost = ' num2str(BestCosts(Iter))]);
end
Conv_History=BestCosts;
Best_Pos=BestPop;
%% Calculate the Euclidean Distance
function o = distance(a,b)
for i=1:size(a,1)
o(1,i)=sqrt((a(i)-b(i))^2);
end
6.2 func_plot.m
% This function draws the benchmark functions
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x; %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
end
6.3 Get_Functions_details.m
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=10;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=10;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=10;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=10;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=10;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=10;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=10;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=10;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=10;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=10;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=10;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=10;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=10;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
6.4 main.m
clear all
clc
close
SearchAgents_no=100; % Number of search agents
Function_name='F21'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)
Max_iteration=1000; % Maximum numbef of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[fMin,bestX,FHO_curve]=FHO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
figure('Position',[290 206 648 287])
%Draw the search space
subplot(1,2,1);
func_plot(Function_name);
title('Test function')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
grid off
%Draw the convergence curve
subplot(1,2,2);
semilogy(FHO_curve,'Color','C')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
%axis tight
legend('FHO')
display(['The best solution obtained by FHO is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton found by FHO is : ', num2str(fMin)]);
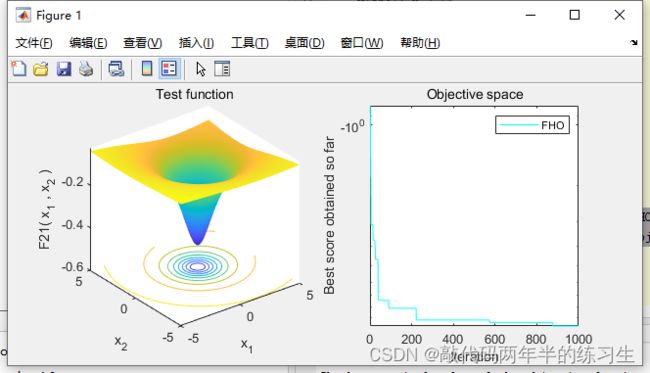
7.运行结果
8.参考文献
[1]Azizi Mahdi,Talatahari Siamak,Gandomi Amir H… Fire Hawk Optimizer: a novel metaheuristic algorithm[J]. Artificial Intelligence Review,2022,56(1).