逆波兰计算器 中缀转化后缀
一.中缀转化后缀
1.具体转换方式
①从左到右进行遍历
②运算数 直接输出.
③左括号直接压入堆栈(括号是最高优先级,无需比较)(入栈后优先级降到最低,确保其他符号正常入栈)
④右括号(意味着括号已结束)不断弹出栈顶运算符并输出直到遇到左括号(弹出但不输出)
⑤运算符将该运算符与栈顶运算符进行比较
如果优先级高于栈顶运算符则压入堆栈(该部分运算还不能进行),
如果优先级低于等于栈顶运算符则将栈顶运算符弹出并输出,然后比较新的栈顶运算符.
(低于弹出意味着前面部分可以运算,先输出的一定是高优先级运算符,等于弹出是因为同等优先级,从左到右运算)
直到优先级大于栈顶运算符或者栈空,再将该运算符入栈.
⑥如果对象处理完毕,则按顺序弹出并输出栈中所有运算符.
2.例子
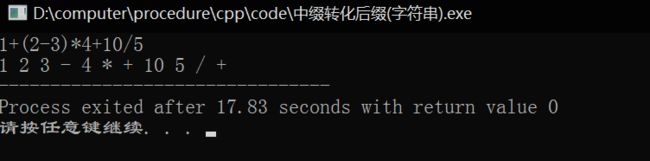
中缀:1+(2-3)*4+10/5
后缀:1 2 3 - 4 * + 10 5 / +
3.代码实现
栈的基本操作
在这里插入代码片#include <stdio.h>
#include - 字符串实现
void Change(SqStack *s, ElemType str[])
{
int i = 0;
ElemType e;
InitStack(s);
while(str[i] != '\0')
{
while(isdigit(str[i])) //过滤数字字符 直接输出 直到下一位不是数字字符打印空格跳出循环
{
printf("%c", str[i++]);
if(!isdigit(str[i]))
{
printf(" ");
}
}
/*加减运算符优先级最低,如果栈顶元素为空则直接入栈,否则将栈中存储
的运算符全部弹栈,如果遇到左括号则停止,将弹出的左括号从新压栈,因为左
括号要和右括号匹配时弹出,这个后面单独讨论。弹出后将优先级低的运算符压入栈中*/
if(str[i] == '+' || '-' == str[i])
{
if(!StackLength(s))
{
Push(s, str[i]);
}
else
{
do
{
Pop(s, &e);
if('(' == e)
{
Push(s, e);
}
else
{
printf("%c ", e);
}
}while(StackLength(s) && '(' != e);
Push(s, str[i]);
}
}
/*当遇到右括号是,把括号里剩余的运算符弹出,直到匹配到左括号为止
左括号只弹出不打印(右括号也不压栈)*/
else if(')' == str[i])
{
Pop(s, &e);
while('(' != e)
{
printf("%c ", e);
Pop(s, &e);
}
}
/*乘、除、左括号都是优先级高的,直接压栈*/
else if('*' == str[i] || '/' == str[i] || '(' == str[i])
{
Push(s, str[i]);
}
else if('\0' == str[i])
{
break;
}
else
{
printf("\n输入格式错误!\n");
return ;
}
i++;
}
//最后把栈中剩余的运算符依次弹栈打印
while(StackLength(s))
{
Pop(s, &e);
printf("%c ", e);
}
}
- #来表示结束
scanf("%c", &c);
while ('#' != c)
{
while(isdigit(c))
{
printf("%c", c);
scanf("%c", &c);
if(!isdigit(c))
{
printf(" ");
}
}
if('+' == c || '-' == c)
{
if(!StackLength(&s))
{
Push(&s, c);
}
else
{
do
{
Pop(&s, &e);
if('(' == e)
{
Push(&s, e);
}
else
{
printf("%c ", e);
}
}while(StackLength(&s) && '(' != e);
Push(&s, c);
}
}
else if(')' == c)
{
Pop(&s, &e);
while('(' != e)
{
printf("%c ", e);
Pop(&s, &e);
}
}
else if('*' == c || '/' == c || '(' == c)
{
Push(&s, c);
}
else if('#' == c)
{
break;
}
else
{
printf("\n输入错误!\n");
}
scanf("%c", &c);
}
while(StackLength(&s))
{
Pop(&s, &e);
printf("%c ", e);
}
return 0;
}
4.结果
二.逆波兰计算器
将输入的后缀表达式输出计算结果
1.代码实现
用栈的链式存储结构
#include //入栈
void Push(LinkStack *s, ElemType e)
{
LinkStackPtr p = (LinkStackPtr) malloc (sizeof(StackNode));
p -> data = e;
p -> next = s -> top;
s -> top = p;
s -> count++;
}
//判断栈是否为空
int StackEmpty(LinkStack s)
{
if(s.top == NULL)
{
printf("空栈");
return 0;
}
return 1;
}
//出栈
void Pop(LinkStack *s, ElemType *e)
{
LinkStackPtr p; //存储要出栈的数据
if(StackEmpty(*s))
{
*e = s -> top -> data;
p = s -> top;
s -> top = s -> top -> next;
free(p);
s -> count--;
}
}
关键部分
int main()
{
LinkStack s;
InitLinkStack(&s);
char c;
double d, e;
char str[10];
int i = 0;
printf("请按输入逆波兰表达式输入待计算数据,数据与运算符之间用空格隔开,以#作为结束标志\n");
scanf("%c",&c);
while(c != '#')
{
while(isdigit(c) || '.' == c) //isdigit(c)判断c是否为数字
{
str[i++] = c;
str[i] = '\0';
if(i >= 10)
{
printf("输入的数据过大\n");
return -1;
}
scanf("%c", &c);
if(' ' == c)
{
d = atof(str); //将字符串转换为double型数据
Push(&s, d);
i = 0;
break;
}
}
switch(c)
{
case'+':
{
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d + e);
break;
}
case'-':
{
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d - e);
break;
}
case'*':
{
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d * e);
break;
}
case'/':
{
Pop(&s, &e);
Pop(&s, &d);
if(0 == e)
{
printf("除数为0 错误!");
return -1;
}
Push(&s, d / e);
break;
}
}
scanf("%c", &c);
}
Pop(&s, &d);
printf("运算结果为:%f\n",d);
return 0;
}