二叉树和树的小问题
先大概说一下二叉树的基本内容。
1. 二叉树
什么是二叉树?
二叉树是一种树形结构,每个结点最多两棵子树,而且子树有左右之分,次序不能颠倒。左右子树也是一棵二叉树。
1.1 二叉树的存储
二叉树可以用数组和链表存储。
1)顺序存储
使用一组地址连续的存储单元依次自上而下,自左而右的顺序存储二叉树上的结点。简单来说,就是用数组存储,存二叉树的顺序是从上到下,从左到右。
顺序存储方式适合完全二叉树或满二叉树。因为数组的长度是固定的,而这种二叉树的空节点少,不会浪费很多数组的地址空间。
// java 定义方式
int[] array = new int[3];
array[0] = 1;
array[2] = 3;
// 或者是
int[] array = {1, 0, 3}; // 0 表示该处节点为空
2)链式存储
由于一般二叉树会有很多节点为空,如果使用顺序存储会导致很多空间浪费掉。所以一般的二叉树使用链式存储比较多。大多情况下,用到的也是链式存储,比如经常使用到的遍历。
链式存储是使用链表节点来存储二叉树中的每个节点。所有需要先定义链表的结点。
// java 定义方式
class TreeNode {
int val;
TreeNode left, right;
// 构造函数
}
1.2 二叉树的遍历
二叉树的遍历方法:前序遍历、中序遍历、后序遍历,应该没有人不知道。以下的代码是使用java实现
1)前序遍历
void preOrder(TreeNode root) {
// 终止条件
if (root == null) return;
getValue(root); // 访问该结点,做一些计算等
preOrder(root.left); // 遍历左结点点
preOrder(root.right); // 遍历右结点
}
2)中序遍历
void preOrder(TreeNode root) {
// 终止条件
if (root == null) return;
preOrder(root.left); // 遍历左结点点
getValue(root); // 访问该结点,做一些计算等
preOrder(root.right); // 遍历右结点
}
3)后序遍历
void preOrder(TreeNode root) {
// 终止条件
if (root == null) return;
preOrder(root.left); // 遍历左结点点
preOrder(root.right); // 遍历右结点
getValue(root); // 访问该结点,做一些计算等
}
4)例子
这三种遍历方法的代码并不难,平常做题的时候也没有很大的问题。但是有一次在极度紧张下,我发现做题时竟然分不清当时用的是哪种遍历,是前序还是中序还是回溯来着??是该用哪种写代码呢??
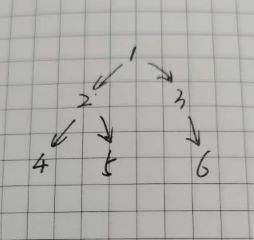
以求树中的最大值、最小值为例。有这样一棵树,通过遍历的方式求出二叉树中的最大值、最小值。
那么,在遍历中,需要记录当前结点的最大值和最小值,下面的图中,[最大值, 最小值] 记录的是当前的最大值和最小值。
前序遍历
走到结点 1 (遍历结点),记录下当前的最大值和最小值 [1, 1] (访问结点),然后遍历左子树,遍历完左子树再右子树。图中圆圈中记录的是结点的访问顺序,前序的遍历顺序和访问顺序相同。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iWOZcCk3-1642662420102)(https://gitee.com/withered-wood/picture/raw/master/20220119234925.jpg")]
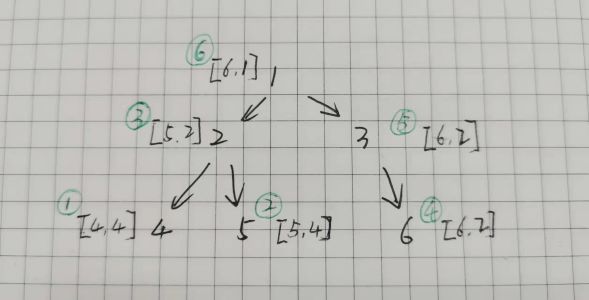
中序遍历
以结点 1 为例,走到结点 1 (遍历结点),不记录。当把左子树的节点访问完之后,然后访问结点 1,也就是记录结点 1 此时的最大值最小值 [5, 1] 。然后再访问结点 1 的右子树。
所以,第一个记录最大值和最小值的结点是结点 4 ,也就是第一个访问的结点是结点 4 。第二个记录最大值和最小值的结点是结点 2 ,也就是第二个访问的结点是结点 2 。
图中圆圈中记录的是结点的访问顺序,中序的遍历顺序和访问顺序不同。
后序遍历
以结点 1 为例,走到结点 1 (遍历结点),不记录。当把左子树的节点访问完之后,然后再访问结点 1 的右子树。最后访问结点 1 ,也就是记录结点 1 此时的最大值最小值 [6, 1] 。
所以,第一个记录最大值和最小值的结点是结点 4 ,也就是第一个访问的结点是结点 4 。第二个记录最大值和最小值的结点是结点 5 ,也就是第二个访问的结点是结点 5 。
图中圆圈中记录的是结点的访问顺序,后序的遍历顺序和访问顺序不同。
遍历顺序的问题就到这里了。下面的代码是求二叉树中的最大值和最小值,代码使用java实现。
int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
public void getMaxDifference(TreeNode root) {
if (root == null) return;
if (root.val > max) max = root.val;
if (root.val < min) min = root.val;
getMaxDifference(root.left);
getMaxDifference(root.right);
}
4)层次遍历
层次遍历是通过队列实现的,以下的代码是使用java实现
// 遍历二叉树,其他什么也没做
void level(TreeNode root) {
LinkedList<TreeNode> queue = new LinkedList<>();
if (root != null) queue.offer(root); // 加入根节点
while (!queue.isEmpty()) {
// 弹出队首节点
TreeNode cur = queue.poll();
// 加入左右节点
if(cur.left != null) queue.offer(cur.left);
if(cur.right != null) queue.offer(cur.right);
}
}
2. 树
二叉树是树,但树不一定是二叉树。所以,二叉树和树的关系就很明显:二叉树可以使用树的东西,树不能使用二叉树的东西。
为什么这里会说到树呢?
因为在一次面试中遇到一道题,是使用数组存储二叉树,数组中的值是它的父节点的下标。嗯嗯,如果把二叉树和树割裂开记忆学习,思维会局限在那一小块。不只是二叉树和树,其他的知识也应该联系在一起,也可以联系在一起。
2.1 树的存储方式
树的存储方式有很多中,即可用顺序存储,也可用链式存储。但是不管哪种存储方式,都要能够唯一的反映树中各节点之间的逻辑关系。这一点,对于二叉树来说也是一样。因为树中有几个子节点,是不确定的,所以不能像二叉树中那样,直接定义两个子节点 left, right ,就可以表示整个树。
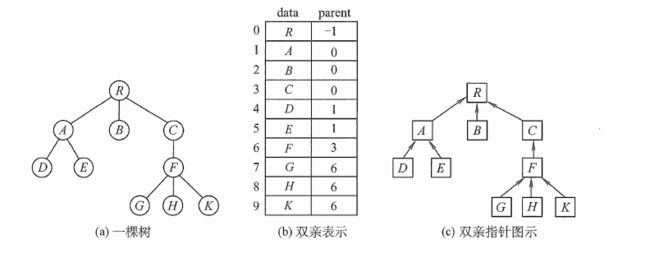
1)双亲表示法
记录的是当前节点的父结点。使用数组存储,存储的是当前节点的父节点在数组中的位置。
正式点的术语说就是,采用一组连续空间来存储每个节点,同时每个节点增加一个变量(指针),用来记录该节点的双亲节点在数组中的位置。
这种结构,找到当前结点的父节点很容易,但是找到当前结点的孩子节点,需要遍历整个树,也就整个存储结构。
上面的树的存储结构,可以表示为以下(使用 java 实现)
// 定义结点
class TreeNode {
int val;
int parent;
// 构造函数
}
// 定义一棵树
TreeNode[] tree = new TreeNode[10];
如果一棵树中节点的值就是数组中的下标,那么还可以不存储 val ,表示如下(使用 java 描述)
int[] tree = new int[10];
举个例子,如果一个数组是 int[] tree = {1, -1, 1, 0} ,那么这棵树表示的就是,根节点是 1, 1 的两个子节点是 0 ,2 , 0 的一个子节点是 3 。
嗯嗯嗯,这个好像是二叉树??嗯,就是二叉树,用数组表示了一棵普通的二叉树(当然了,这种表示方式不能区分左右子节点)。
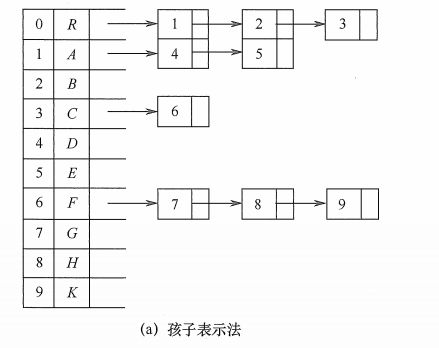
2)孩子表示法
记录的是当前节点的所有子结点。
正式点的术语说就是,每个结点的孩子都用单链表连接起来,形成一个线性结构,
这种结构,找到当前结点的孩子节点很容易,但是找到当前结点的父节点,需要遍历整个树,也就整个存储结构。
上面的树的存储结构,可以表示为以下(使用 java 实现)
// 定义结点
class TreeNode {
int val;
List<TreeNode> child;
// 构造函数
}
// 定义一棵树
TreeNode[] tree = new TreeNode[10];
如果一棵树中节点的值就是数组中的下标,那么还可以不存储 val ,表示如下(使用 java 描述)
List<Integer>[] tree = new List[10];
3)孩子兄弟表示法
记录的是当前节点的第一个子结点和下一个兄弟节点。孩子兄弟表示法又称二叉树链表法, 也就是将二叉链表作为树的存储结构,一个子结点指向孩子结点,一个子结点指向兄弟节点。
上面的树的存储结构,可以表示为以下(使用 java 实现)
// 定义结点
class TreeNode {
int val;
TreeNode firstChild, nextsibling;
// 构造函数
}
// 定义一棵树
TreeNode[] tree = new TreeNode[10];
参考资料
王道数据结构书籍