LeetCode刷题总结 - LeetCode 热题 100 - 持续更新
LeetCode 热题 100
- 其他系列
- 哈希
-
- 1. 两数之和
- 49. 字母异位词分组
- 128. 最长连续序列
- 双指针
-
- 27. 移除元素
- 283. 移动零
- 11. 盛最多水的容器
- 剑指 Offer II 007. 数组中和为 0 的三个数
- 42. 接雨水
- 滑动窗口
-
- 438. 找到字符串中所有字母异位词
- 3. 无重复字符的最长子串
- 字串
-
- 560. 和为 K 的子数组
- 剑指 Offer 59 - I. 滑动窗口的最大值
- 普通数组
-
- 最大子数组和
- 56. 合并区间
- 189. 轮转数组
- 238. 除自身以外数组的乘积
- 矩阵
-
- 73. 矩阵置零
- 54. 螺旋矩阵
- 48. 旋转图像
- 240. 搜索二维矩阵 II
- 链表
-
- 160. 相交链表
- 206. 反转链表
- 234. 回文链表
- 141. 环形链表(基础模板题)
- 142. 环形链表 II
- 21. 合并两个有序链表(模板题)
- 2. 两数相加
- 19. 删除链表的倒数第 N 个结点
- 24. 两两交换链表中的节点
- 25. K 个一组翻转链表
- 138. 复制带随机指针的链表
- 148. 排序链表
- 23. 合并 K 个升序链表
- 二叉树
-
- 94. 二叉树的中序遍历
- 104. 二叉树的最大深度
- 226. 翻转二叉树
- 101. 对称二叉树
- 543. 二叉树的直径
- 102. 二叉树的层序遍历
- 108. 将有序数组转换为二叉搜索树
- 98. 验证二叉搜索树
- 剑指 Offer 54. 二叉搜索树的第k大节点
- 199. 二叉树的右视图
- 114. 二叉树展开为链表
- 105. 从前序与中序遍历序列构造二叉树
- LCR 050. 路径总和 III
- 236. 二叉树的最近公共祖先
- 图论
-
- 200. 岛屿数量
- 994. 腐烂的橘子
- 207. 课程表
- 208. 实现 Trie (前缀树)
- 回溯
-
- 17. 电话号码的字母组合
- 77. 组合
- 39. 组合总和
- 剑指 Offer 34. 二叉树中和为某一值的路径
- 46. 全排列
- 47. 全排列 II
- 78. 子集
- 51. N 皇后
- 22. 括号生成
- 131. 分割回文串
- 二分查找
-
- 35. 搜索插入位置
- 74. 搜索二维矩阵
- 34. 在排序数组中查找元素的第一个和最后一个位置
- JZ11 旋转数组的最小数字(存在重复值)
- 153. 寻找旋转排序数组中的最小值(不包含重复值)
- 33. 搜索旋转排序数组
- 栈
-
- 20. 有效的括号
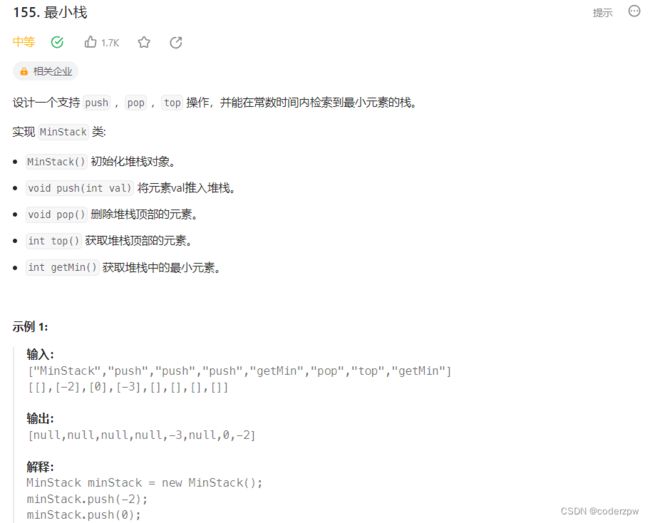
- 155. 最小栈
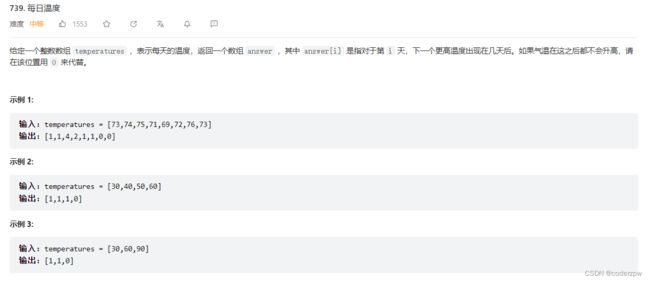
- 739. 每日温度
- 42. 接雨水
- 堆
-
- 数组中的第K个最大元素
- 347. 前 K 个高频元素
- 295. 数据流的中位数
- 贪心算法
-
- 55. 跳跃游戏
- 45. 跳跃游戏 II
- 763. 划分字母区间
- 动态规划
-
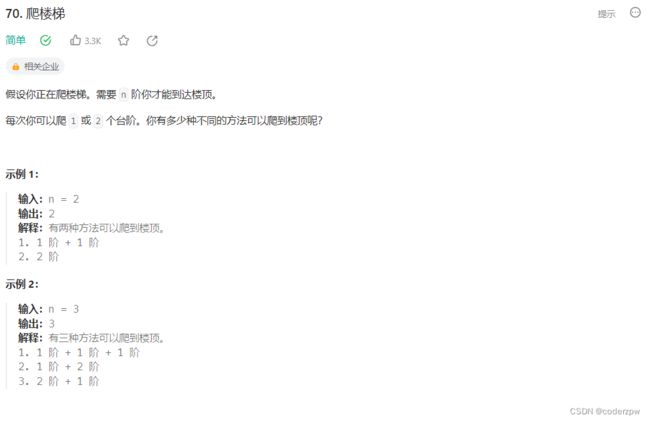
- 70. 爬楼梯
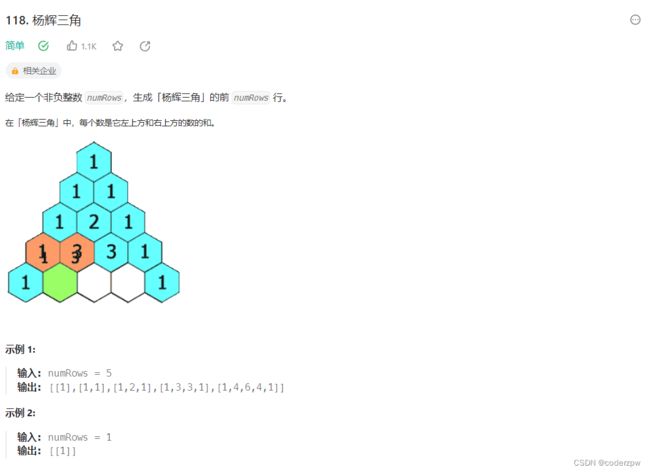
- 118. 杨辉三角
- 322. 零钱兑换
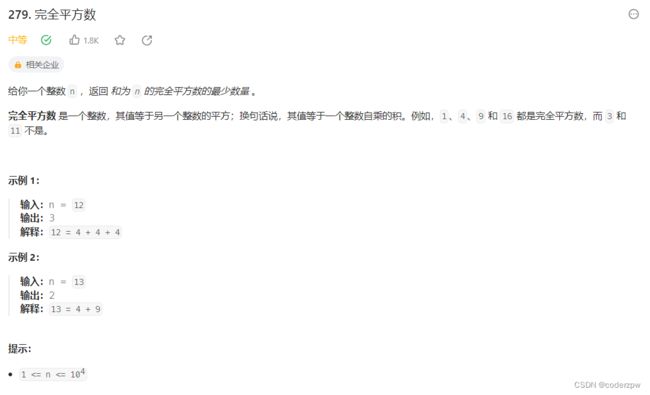
- 279. 完全平方数
- 139. 单词拆分
- 300. 最长递增子序列
- 和最大子数组
- 152. 乘积最大子数组
- 416. 分割等和子集
- 打家劫舍系列
-
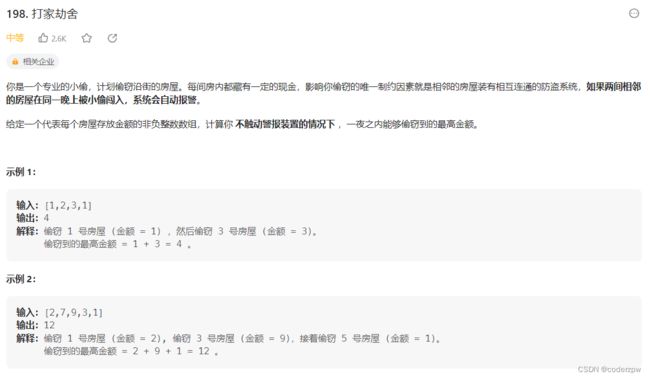
- 198. 打家劫舍
- 213. 打家劫舍 II
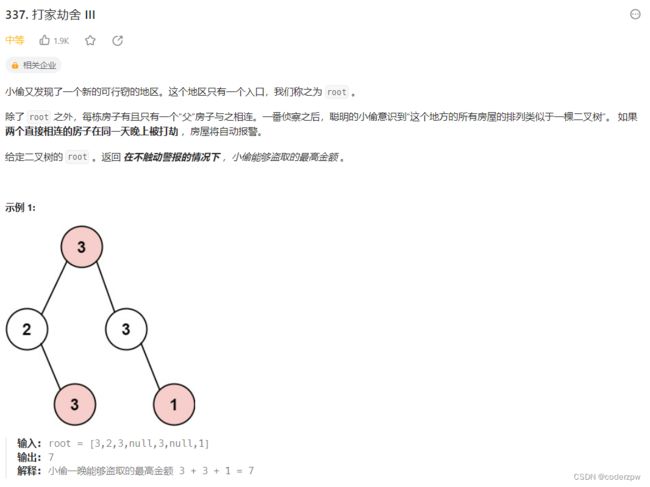
- 337. 打家劫舍 III
- 多维动态规划
-
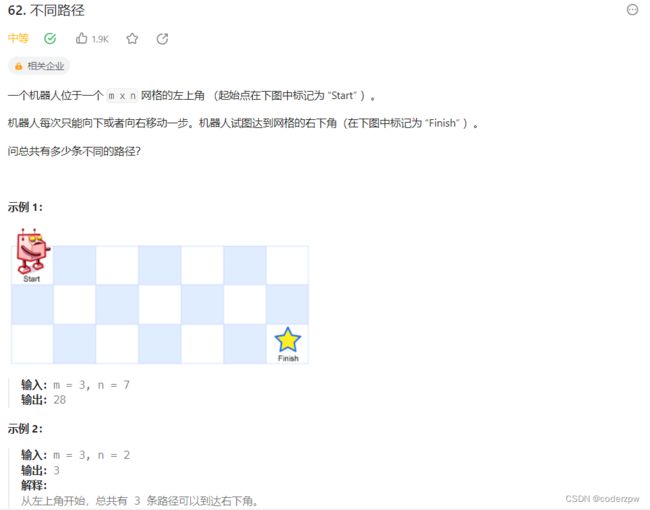
- 62. 不同路径
- 63. 不同路径 II
- 64. 最小路径和
- 5. 最长回文子串(中心扩展法,非动态规划解法)
-
- 解法一:暴力 - 遍历所有字串
- 解法二:中心扩展法
- 1143. 最长公共子序列
- 技巧
-
- 169. 多数元素
- 136. 只出现一次的数字
- 75. 颜色分类
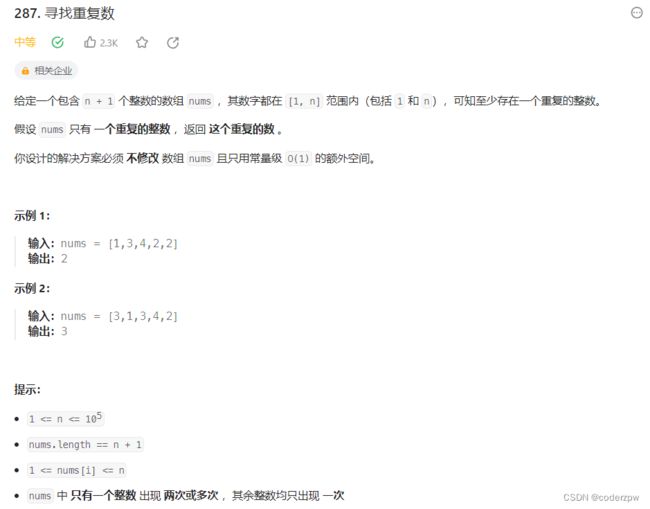
- 287. 寻找重复数
其他系列
【LeetCode刷题总结 - 剑指offer系列 - 持续更新】
【LeetCode刷题总结 - 面试经典 150 题 -持续更新】
哈希
1. 两数之和
分析:
- 空间换时间的思想,将当前值 以及对应下标信息 存储在map中
核心代码:
// 初始化:存储 某个值 以及 在nums中的位置信息
HashMap<Integer, Integer> tempMap = new HashMap();
// 如果目标值 存在tempMap中,则说明找到了结果
if(tempMap.containsKey(another)) {
res[0] = i;
res[1] = tempMap.get(another);
return res;
}
// 主流程:把当前值 及 对应位置信息存入到map中
tempMap.put(nums[i], i);
代码:
class Solution {
public int[] twoSum(int[] nums, int target) {
// 初始化map: 【值:下标】
HashMap<Integer, Integer> tempMap = new HashMap();
int[] res = new int[2];
for(int i=0; i<nums.length; i++) {
Integer another = target - nums[i];
// 如果目标值 存在tempMap中,则说明找到了结果
if(tempMap.containsKey(another)) {
res[0] = i;
res[1] = tempMap.get(another);
return res;
}
// 将【值:下标】 存储在map中 (常规套路,在写代码时进入for后 就可以先写这一步)
tempMap.put(nums[i], i);
}
return res;
}
}
49. 字母异位词分组
分析:
由于互为字母异位词的两个字符串包含的字母相同,因此对两个字符串分别进行排序之后得到的字符串一定是相同的,故可以将排序之后的字符串作为哈希表的键。
代码:
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<String, List<String>>();
for (String str : strs) {
char[] array = str.toCharArray();
// 字母异位词 排序后一定相同
Arrays.sort(array);
String key = new String(array);
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(str);
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}
}
128. 最长连续序列
分析:
参考题解:【【超小白】哈希集合/哈希表/动态规划/并查集四种方法,绝对够兄弟们喝一壶的!】
- 首先遍历数组,将数据存储到
set中,set有两个作用:- 作用1:使用
hashSet判断元素是否存在,时间复杂度为O(1) - 作用2:元素去重
- 作用1:使用
- 遍历
set,计算元素连续累加的最大长度。若cur-1存在,则没必要计算,原因:- 原因1:如果
num-1已经在数组中的话,那么num-1肯定会进行相应的+1遍历,然后遍历到num - 原因2:而且从
num-1开始的+1遍历必定比从num开始的+1遍历得到的序列长度更长
- 原因1:如果
代码:
class Solution {
public int longestConsecutive(int[] nums) {
int res = 0;
Set<Integer> set = new HashSet();
for(int num: nums) {
set.add(num);
}
// 遍历去重后的set
for(int num: set) {
int cur = num;
/**
* 若存在 cur-1,那么我们是没必要计算的,因为
* 1. 如果num-1已经在数组中的话,那么num-1肯定会进行相应的+1遍历,然后遍历到num
* 2. 而且从num-1开始的+1遍历必定比从num开始的+1遍历得到的序列长度更长
* 结论:我们便可将在一个连续序列中的元素让其只在最小的元素才开始+1遍历
*/
if(!set.contains(cur-1)) {
// 计算累加连续最大长度
while(set.contains(cur+1)) {
cur++;
}
// 更新最大值
res = Math.max(res, cur - num + 1);
}
}
return res;
}
}
双指针
27. 移除元素
分析:
- 新增一个指针
left,[0,left)之间的元素就是!=val的 - 遍历数组,判断每个元素是否等于
val,!= val则添加到nums[left],left++
参考动画:https://leetcode.cn/problems/remove-element/solution/xue-sheng-wu-de-nu-peng-you-du-neng-kan-nk7yy/
代码:
class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;
// 遍历数组,判断每个元素
for(int right=0; right<nums.length; right++) {
if(nums[right] != val) {
nums[left] = nums[right];
left++;
}
}
return left;
}
}
283. 移动零
分析:
跟上题类似,只不过目标值变成了0
代码:
class Solution {
public void moveZeroes(int[] nums) {
int len = nums.length;
int left = 0;
for(int i=0; i<len; i++) {
if(nums[i] != 0) {
nums[left++] = nums[i];
}
}
for(int i=left; i<len; i++) {
nums[i] = 0;
}
}
}
11. 盛最多水的容器
分析:
借鉴题解:https://leetcode.cn/problems/container-with-most-water/solution/container-with-most-water-shuang-zhi-zhen-fa-yi-do/
结论:左右指针,谁的高度越低,谁就往中间移动
- 若向内移动短板,水槽的短板
min(h[i], h[j])可能变大,因此下个水槽面积可能增大 - 若向内移动长板,水槽的短板
min(h[i], h[j])不变或变小,因此下个水槽面积一定变小
流程:
- 初始化:双指针
left,right分列水槽的两端 - 循环收窄:直到双指针相遇则跳出
- 更新面积最大值
max - 选定两板高度中的短板,向中间收窄一格
- 更新面积最大值
- 返回值:返回面积最大值即可
代码:
class Solution {
public int maxArea(int[] height) {
int max = Integer.MIN_VALUE;
int left = 0;
int right = height.length-1;
while(left < right) {
int area = (right - left) * Math.min(height[left], height[right]);
max = Math.max(max, area);
// 谁低谁往中间移动
if(height[left] < height[right]) {
left++;
} else {
right--;
}
}
return max;
}
}
剑指 Offer II 007. 数组中和为 0 的三个数
【剑指 Offer II 007. 数组中和为 0 的三个数】
![]()
分析:
- 先排序
- 通过枚举
i确定第一个数,另外两个指针left,right分别从左边i + 1和右边length - 1往中间移动,找到满足nums[left] + nums[right] == -nums[i]的所有组合 - 去重:因为是有序序列,因此我们可以用如下方式去重(重点,看代码细细品味)
代码:
class Solution {
/**
* 【重要】:因为数据是排好序的,因此我们哪样处理才会去重
* 细细品味,其实每次去重,都是保证 三元组中每一个元素,这一次 与 下一次 数据不同(每一个元素都是如此)
*/
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList();
Arrays.sort(nums);
for(int i=0; i<nums.length; i++) {
// 若当前值与上一个相同,则没必要再重新搞一遍了,否则会重复
if(i > 0 && nums[i] == nums[i-1]) {
continue;
}
int target = -nums[i];
int left = i+1;
int right = nums.length-1;
while(left < right) {
int sum = nums[left] + nums[right];
if(sum == target) {
res.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 找下一个跟 当前tempL不同的值作为新的left(因为数组是有序的,因此这样可以保证去重)
int tempL = nums[left++];
while(left < right && nums[left] == tempL) {
left++;
}
// 找下一个跟 当前tempR不同的值作为新的right(同理)
int tempR = nums[right--];
while(left < right && nums[right] == tempR) {
right--;
}
}
if(sum < target) {
left++;
} else if ( sum > target) {
right--;
}
}
}
return res;
}
}
42. 接雨水
分析:
参考视频:【单调栈,经典来袭!LeetCode:42.接雨水】
建议先做上一题
- 找到
较低点的前一个较大值和后一个较大值,则可以算较低点相对于前、后两个较大点所接的雨水(横向求解,水平求解) - 维护一个
单调栈(存储下标),若当前值大于栈顶元素,则栈顶元素就是较低点,栈顶第二个元素就是较低点的前一个较大点,当前值就是较低点的下一个较大点
代码:
class Solution {
public int trap(int[] height) {
// stack维护一个单调栈(非递减),存储下标
Stack<Integer> stack = new Stack();
// 记录接雨水的总数
int sum = 0;
for(int i=0; i<height.length; i++) {
int cur = height[i];
// 若栈顶元素 小于 当前值则弹出(表示当前值是栈顶元素的后续第一个较大者)
while(!stack.isEmpty() && height[stack.peek()] < cur) {
// nextHeight:下个较大值(下标)
int nextHeight = i;
// mid:就是中间点(下标)
int mid = stack.pop();
if(stack.isEmpty()) { // 若为空 则直接跳过,不处理
break;
}
// preHeight:前一个较大值(下标)
int preHeight = stack.peek();
// 高度差
int diffY = Math.min(height[preHeight], height[nextHeight]) - height[mid];
// 宽度差
int diffX = nextHeight - preHeight - 1;
// 面积累计
sum += diffX * diffY;
}
stack.push(i);
}
return sum;
}
}
滑动窗口
438. 找到字符串中所有字母异位词
分析:
参考题解:【固定滑动窗口求解LC438】
代码:
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList();
int lenS = s.length();
int lenP = p.length();
if(lenS < lenP) { // 若 s长度 < p长度 ,则不存在解
return new ArrayList();
}
// 用于维护滑动窗口过程中每个字母的数量
int[] windowCount = new int[26];
// 用于统计字符p的每个字符的数量
int[] pCount = new int[26];
// 初始统计
for(int i=0; i<lenP; i++) {
windowCount[s.charAt(i) - 'a']++;
pCount[p.charAt(i) - 'a']++;
}
// [left, right] 维护滑动窗口区间, 区间内的windowCount若与pCount相同,则满足解条件
for(int left=0, right=lenP-1; right<lenS; left++, right++) {
if(Arrays.equals(windowCount, pCount)) {
res.add(left);
}
// 左指针移动
windowCount[s.charAt(left) - 'a']--;
// 右指针移动
if(right + 1 < lenS) {
windowCount[s.charAt(right + 1) - 'a']++;
}
}
return res;
}
}
3. 无重复字符的最长子串
【无重复字符的最长子串】
分析:
解题思路:
该题是一道滑动窗口的问题。
滑动窗口的一般套路:左区间手动改变,有区间for循环累加
B站上视频链接:
https://www.bilibili.com/video/BV1BV411i77g
https://www.bilibili.com/video/BV1w5411E7EP
总结注意点:
- 和第一道题【1. 两数之和】类似点在于,都可以使用 一个map 来记录【值:下标】
- 使用
双指针构建滑动窗口的 经典问题。(套路:左边界手动改变 右边界自动累加) l和r滑动窗口的区间[l,r]表示的就是当前所维护的不重复的字串l = Math.max(l, map.get(curChar) + 1),这里取得是map.get(curChar) + 1,别忘了+1了。如果不+1的话,那么字串可能是abca这种,即第一个字符与后面那个字符重复
代码:
class Solution {
public int lengthOfLongestSubstring(String s) {
// 判空处理
if(null == s || s.length() == 0) {
return 0;
}
// 初始化map: 【值:下标】
HashMap<Character, Integer> map = new HashMap();
// 定义滑动窗口最左侧指针
int l = 0;
// 最大长度
int maxLength = 0;
// r可以理解为 滑动窗口最右侧指针
for(int r = 0; r < s.length(); r++) {
char curChar = s.charAt(r);
// 若map中之前存过这个值的下标,则让left指针右移
if(map.containsKey(curChar)) {
// 目的:更新l 为 l、map(curChar)最右侧的下标
// Math.max的好处:我们不需要考虑这个值是否在滑动窗口内
l = Math.max(l, map.get(curChar) + 1);
}
// 更新最大长度
maxLength = Math.max(maxLength, r - l + 1);
// 将【值:下标】 存储在map中 (常规套路,在写代码时进入for后 就可以先写这一步)
map.put(curChar, r);
}
return maxLength;
}
}
字串
560. 和为 K 的子数组
分析:
参考视频:【560. 和为 K 的子数组 Subarray Sum Equals K【LeetCode 力扣官方题解】】
参考评论:
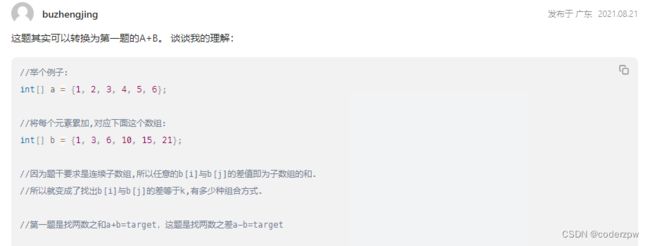
代码:
class Solution {
public int subarraySum(int[] nums, int k) {
/**
【这题其实可以转换为第一题的A+B。 谈谈我的理解:】(参考用户buzhengjing的评论)
//举个例子:
int[] a = {1, 2, 3, 4, 5, 6};
//将每个元素累加,对应下面这个数组:
int[] b = {1, 3, 6, 10, 15, 21};
//因为题干要求是连续子数组,所以任意的b[i]与b[j]的差值即为子数组的和.
//所以就变成了找出b[i]与b[j]的差等于k,有多少种组合方式.
//第一题是找两数之和a+b=target,这题是找两数之差a-b=target
*/
int count = 0;
int len = nums.length;
// 记录前缀和
int[] dp = new int[len];
dp[0] = nums[0];
for(int i=1; i<len; i++) {
dp[i] = dp[i-1] + nums[i];
}
// 记录前缀和 的个数, key:前缀和 value: 个数
Map<Integer, Integer> map = new HashMap();
/**
* 前缀和为0,要赋值为1。
* 例子:nums = [3,...], k = 3,和 nums = [1, 1, 1,...], k = 3 这两种情况 刚开始需要得到前缀和为0的个数,如果给0 的话结果就会漏记算这种情况
*/
map.put(0, 1);
// 遍历前缀和
for(int i=0; i<len; i++) {
int target = dp[i] - k;
count += map.getOrDefault(target, 0); // 更新count
map.put(dp[i], map.getOrDefault(dp[i], 0) + 1); // 累加前缀和的个数
}
return count;
}
}
剑指 Offer 59 - I. 滑动窗口的最大值
【剑指 Offer 59 - I. 滑动窗口的最大值】
![]()
分析:
其实思路和上一题是一致的,可以在上一题的基础上进行处理
- 没达到滑动窗口大小时(大小为
K),不需要移除头部元素,直接添加尾部元素(调用push_back) - 达到滑动窗口大小时,存储当前队列最大值(
max_value) - 达到滑动窗口大小后,需要先移除头部元素(
pop_front),再添加尾部元素(push_back),然后存储当前队列最大值(max_value)
代码:
class Solution {
// 存储实际的值
Queue<Integer> queue;
// 双端队列维护最大值,单调递减
Deque<Integer> deque;
public void init() {
queue = new LinkedList();
deque = new LinkedList();
}
public int max_value() {
if(deque.isEmpty()) {
return -1;
}
// 返回队列头部元素,递增序列 头部最大
return deque.peekFirst();
}
public void push_back(int value) {
queue.offer(value);
// 移除掉队列中比自己小的值(篮球队长模型)
while(!deque.isEmpty() && deque.peekLast() < value) {
deque.pollLast();
}
// 最后添加到队尾
deque.addLast(value);
}
public int pop_front() {
if(queue.isEmpty()) {
return -1;
}
// 若队头元素 就是 最大队列的头部,则移除掉 最大队列头部
if(queue.peek().equals(deque.peek())) {
deque.poll();
}
// 最终调用队列的poll
return queue.poll();
}
public int[] maxSlidingWindow(int[] nums, int k) {
// 存储结果
int[] res = new int[nums.length - k + 1];
init();
// 没达到滑动窗口大小时(大小为K),不需要移除最前面元素
for(int i=0; i<k; i++) {
push_back(nums[i]);
}
int index = 0;
res[index++] = max_value();
for(int i=k; i<nums.length; i++) {
pop_front();
push_back(nums[i]);
res[index++] = max_value();
}
return res;
}
}
简化版:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int len = nums.length;
int[] res = new int[len - k + 1];
Deque<Integer> maxQueue = new LinkedList();
for(int i=0; i<k; i++) {
while(!maxQueue.isEmpty() && nums[i] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[i]);
}
int idx = 0;
res[idx++] = maxQueue.peek();
for(int i=k; i<len; i++) {
// 删除元素
if(maxQueue.peek().equals(nums[i-k])) {
maxQueue.poll();
}
// 添加新的元素
while(!maxQueue.isEmpty() && nums[i] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[i]);
// 储存最大值
res[idx++] = maxQueue.peek();
}
return res;
}
}
普通数组
最大子数组和
分析:
技巧:像这种最大、最小 的 子数组、子序列,我们在定义动态数组时,大多数这样定义:dp[i] = 以下标i 值为结尾的 子数组 或者 子序列
- 遍历
nums,填写dp数组 dp[i]以nums[i]结尾;若dp[i-1] < 0,则没必要加上dp[i-1]了(因为加上去则会使dp[i]更小),dp[i] = nums[i];否则dp[i] = nums[i] + dp[i-1]
代码:
class Solution {
public int maxSubArray(int[] nums) {
if(nums.length == 0) {
return 0;
}
// dp定义: 表示以 i下标值 结尾的子数组的和
int[] dp = new int[nums.length];
dp[0] = nums[0];
int maxSubArrayValue = dp[0];
for(int i=1; i<nums.length; i++) {
// 若dp[i-1] 为负数,则以i结尾的子数组就没必要加上前面的了(因为加上去,只会让数组和更小)
if(dp[i-1] < 0) {
dp[i] = nums[i];
} else {
dp[i] = dp[i-1] + nums[i];
}
// 若dp[i] 大于 最大值,则更新最大值
if(dp[i] > maxSubArrayValue) {
maxSubArrayValue = dp[i];
}
}
return maxSubArrayValue;
}
}
56. 合并区间
【56. 合并区间】
分析:
参考文章:【秒懂力扣区间题目:重叠区间、合并区间、插入区间】
- 遍历
intervals - 若
interval与res的最后一个元素区间重合,则合并最后一个区间 - 否则 则直接加入到
res中
代码:
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new ArrayList();
// 升序排列
Arrays.sort(intervals, (v1,v2) -> v1[0] - v2[0]);
// 遍历intervals,更新res
for(int[] interval: intervals) {
if(!res.isEmpty() && interval[0] <= res.get(res.size()-1)[1]) { // 重叠了,则更新res的最后一个元素
// 拿到 res的最后一个元素
int[] last = res.get(res.size()-1);
// 更新last[1]
last[1] = Math.max(last[1], interval[1]);
} else { // 不重叠则直接更新
res.add(interval);
}
}
int[][] res1 = new int[res.size()][2];
for(int i=0; i<res.size(); i++) {
for(int j=0; j<2; j++) {
res1[i][j] = res.get(i)[j];
}
}
return res1;
}
}
189. 轮转数组
分析:
- 步骤一:整体翻转,
[1,2,3,4,5,6,7]->[7,6,5,4,3,2,1] - 步骤二:数组截断,分成两段,若k=3,则
[7,6,5,4,3,2,1]->[7,6,5]、[4,3,2,1] - 步骤三:分别对两段数组进行翻转,
[7,6,5]、[4,3,2,1]->[5,6,7]、[1,2,3,4] - 步骤四:拼接两段,
[5,6,7]、[1,2,3,4]->[5,6,7,1,2,3,4]
代码:
class Solution {
/**
* 因为我们实际上并没有,分割数组(所有操作都是在原数组上),因此【步骤二】 和 【步骤四】是可以省略的
*/
public void rotate(int[] nums, int k) {
// 注意,该题的k有可能大于数组的长度,因此我们要提前取余
k = k % nums.length;
// 步骤一:整体翻转,[1,2,3,4,5,6,7] -> [7,6,5,4,3,2,1]
reverse(nums, 0, nums.length-1);
// 步骤二:数组截断,分成两段,若k=3,则[7,6,5,4,3,2,1] -> [7,6,5]、[4,3,2,1]
// 步骤三:分别对两段数组进行翻转,[7,6,5]、[4,3,2,1] -> [5,6,7]、[1,2,3,4]
reverse(nums, 0, k-1);
reverse(nums, k, nums.length-1);
// 步骤四:拼接两段,[5,6,7]、[1,2,3,4] -> [5,6,7,1,2,3,4]
}
/**
* 翻转数组中元素 [a,b,c,d] -> [d,c,b,a]
*/
public void reverse(int[] nums, int left, int right) {
while(left < right) {
swap(nums, left, right);
left++;
right--;
}
}
/**
* 交换数组中 index1 和index2 的位置
*/
public void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
238. 除自身以外数组的乘积
分析:
解题思路:
B站上视频连接:https://www.bilibili.com/video/BV1xV411f773
- 利用类似于动态规划的思想,构建
[0,i]的乘积数组,即i及i之前的所有数的乘积 - 利用类似于动态规划的思想,构建
[i,n-1]的乘积数组,即i及i之后的所有数的乘积 - 最终根据题意
res[i] = cj1[i-1] * cj2[i+1],求最终结果集
代码:
public class Solution {
public int[] multiply(int[] A) {
int n = A.length;
// 用于存放 i及i之前的所有乘积(包含i:[0,i])
int[] cj1 = new int[n];
// 用于存放 i及i之后的所有乘积(包含i:[i,n-1])
int[] cj2 = new int[n];
// 用于存放那结果集
int[] res = new int[n];
// 类似于动态规划的求法,求cj1。[0,i]
for(int i=0; i<n; i++) {
// 若i为0,则区A[0] 边界条件
if(i == 0)
cj1[i] = A[0];
else // 动态规划
cj1[i] = cj1[i-1] * A[i];
}
// 类似于动态规划的求法,求cj2。[i,n-1]。 同上
for(int i=n-1; i>=0; i--) {
if(i == n-1)
cj2[i] = A[n-1];
else
cj2[i] = cj2[i+1] * A[i];
}
// 最后根据题意,求结果集
for(int i=0; i<n; i++) {
if(i == 0)
res[i] = cj2[i+1];
else if(i == n-1)
res[i] = cj1[i-1];
else
res[i] = cj1[i-1] * cj2[i+1];
}
return res;
}
}
矩阵
73. 矩阵置零
分析:
参考视频:【【LeetCode 每日一题】73. 矩阵置零 | 手写图解版思路 + 代码讲解】
代码:
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
boolean flag_row0 = false;
boolean flag_col0 = false;
// 遍历第一行是否存在0?
for(int i=0; i<n; i++) {
if(matrix[0][i] == 0) flag_row0 = true;
}
// 遍历第一列是否存在0?
for(int i=0; i<m; i++) {
if(matrix[i][0] == 0) flag_col0 = true;
}
// i、j 都从下标1 开始遍历(否则会错误)
for(int i=1; i<m; i++) {
for(int j=1; j<n; j++) {
if(matrix[i][j] == 0) {
// 若当前位置为0,则将第一行、第一列对应的位置置0
matrix[0][j] = 0;
matrix[i][0] = 0;
}
}
}
// i、j 都从下标1 开始遍历(否则会错误)
for(int i=1; i<m; i++) {
for(int j=1; j<n; j++) {
if(matrix[0][j] == 0 || matrix[i][0] == 0) {
matrix[i][j] = 0;
}
}
}
if(flag_row0) {
for(int i=0; i<n; i++) {
matrix[0][i] = 0;
}
}
if(flag_col0) {
for(int i=0; i<m; i++) {
matrix[i][0] = 0;
}
}
}
}
54. 螺旋矩阵
分析:
参考bilibili视频:【LeetCode力扣刷题 | 剑指Offer 29. 顺时针打印矩阵】
代码:
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
int left = 0;
int right = matrix[0].length - 1;
int top = 0;
int bottom = matrix.length - 1;
List<Integer> res = new ArrayList();
while(true) {
// 打印最上边的
for(int i=left; i<=right; i++) {
res.add(matrix[top][i]);
}
top++;
if(top > bottom) break;
// 打印最右边的
for(int i=top; i<=bottom; i++) {
res.add(matrix[i][right]);
}
right--;
if(right < left) break;
// 打印最下边的
for(int i=right; i>=left; i--) {
res.add(matrix[bottom][i]);
}
bottom--;
if(bottom < top) break;
// 打印最左边的
for(int i=bottom; i>=top; i--) {
res.add(matrix[i][left]);
}
left++;
if(left > right) break;
}
return res;
}
}
48. 旋转图像
分析:
- 先沿左上 到 右下 的中心斜线反转
- 再沿数轴中心反转
参考视频:【【LeetCode 每日一题】48. 旋转图像 | 手写图解版思路 + 代码讲解】
代码:
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 沿对角线反转
for(int i=0; i<n; i++) {
for(int j=0; j<i; j++) { // 注意j的范围
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// 沿中心竖线反转
for(int i=0; i<n; i++) {
for(int j=0; j<n/2; j++) { // 注意j的范围
int temp = matrix[i][j];
matrix[i][j] = matrix[i][n-j-1];
matrix[i][n-j-1] = temp;
}
}
}
}
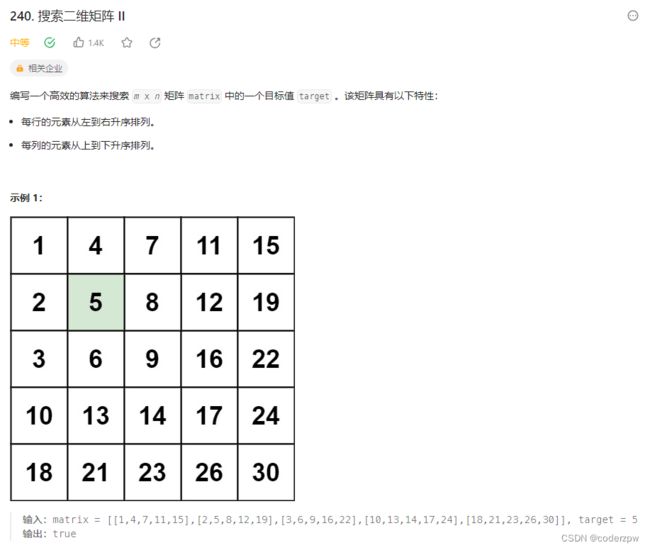
240. 搜索二维矩阵 II
分析:
首先题中说明:
每一行都按照从左到右递增的顺序排序
每一列都按照从上到下递增的顺序排序。
那么一看数据是有序的, 那么我们肯定第一时间想到二分查找法。但在着整个二维数组中好像没法直接使用二分查找,但是我们可以使用二分查找的思想。
二分查找思想: 每一轮比较首先获取一个特殊值,然后让目标值与该值进行比较,每次比较都能排除一些数据进而缩小搜索的范围。
解决该题我们用的方法和二叉查找法类似,也是每次都取一个特殊值与目标值比较,每轮都排除一部分数据进而缩小数据的查找范围

B站上讲解视频:
https://www.bilibili.com/video/BV12J411i7A6
https://www.bilibili.com/video/BV1Tt411F7YD?spm_id_from=333.999.0.0
代码:
class Solution {
public boolean searchMatrix(int[][] array, int target) {
// 套路模板 先判空
if(array.length == 0) return false;
// row表示有几行,col表示有几列。
int row = array.length;
int col = array[0].length;
// 我们取右上角的值
int x = 0; int y = col - 1;
// 不断排除一列或者一行,不断缩小范围
while(x <= row-1 && y >= 0) {
if(target > array[x][y]) {
// 排除头一行的数据
x++;
}else if (target < array[x][y]) {
// 排除后一列的数据
y--;
}else {
return true;
}
}
// 若判处完所有数据仍没有找目标值 该值不存在
return false;
}
}
链表
160. 相交链表
版本一
import java.util.*;
/**
* 暴力解法
*/
public class Solution {
public ListNode getIntersectionNode(ListNode pHead1, ListNode pHead2) {
HashSet<ListNode> set = new HashSet();
// 首先遍历第一个链表的所有节点 并将节点存入带set中
while(pHead1 != null) {
set.add(pHead1);
pHead1 = pHead1.next;
}
// 遍历第二个链表 如果出现节点包含在set中 则说明该节点是链表1和链表2的公共节点
while(pHead2 != null) {
if(set.contains(pHead2)) {
return pHead2;
}
pHead2 = pHead2.next;
}
return null;
}
}
心得:
- 暴力可以解决大多数问题
set.contains(xxx)判断set中是否存在xxx这个对象
版本二
public class Solution {
public ListNode getIntersectionNode(ListNode pHead1, ListNode pHead2) {
int size1 = 0; // 记录链表1的长度
int size2 = 0; // 记录链表2的长度
ListNode cur1 = pHead1;
ListNode cur2 = pHead2;
// 算出链表1 的长度
while(cur1 != null) {
size1++;
cur1 = cur1.next;
}
// 算出链表2 的长度
while(cur2 != null) {
size2++;
cur2 = cur2.next;
}
cur1 = pHead1;
cur2 = pHead2;
// 相当于链表1和链表2 在一个等长的链表上 依次后移,如果两指针相同 则一定是第一个相交点
while(cur1 != cur2) {
// 先走链表2 的长度 再遍历链表1
if(size2 != 0) {
size2--;
}else {
cur1 = cur1.next;
}
// 先走链表1 的长度 再遍历链表2
if(size1 != 0) {
size1--;
}else {
cur2 = cur2.next;
}
}
return cur1;
}
}
心得:
- 有时候解题可以换一种思路
版本三
public class Solution {
public ListNode getIntersectionNode(ListNode pHead1, ListNode pHead2) {
// p1 初始指向pHead1
ListNode p1 = pHead1;
// p2 初始指向pJead2
ListNode p2 = pHead2;
// 遍历 p1 和 p2
while(p1 != p2) {
// 若p1走链表1走到头 则开始走链表2
if(p1 == null)
p1 = pHead2;
else // 没走到头就后移
p1 = p1.next;
// p2 同上
if(p2 == null)
p2 = pHead1;
else
p2 = p2.next;
}
// 最终p1肯定等于p2, 因为他俩要么都是公共点,要么都为null
return p1;
}
}
206. 反转链表
分析:
- 双指针,前指针-
pre,当前指针-cur - 局部翻转实现整体翻转
代码:
public class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null; // 前一个节点
ListNode cur = head; // 当前节点 (该引用初始指向head头结点)
while(cur != null) {
// 1、创建一个新引用指向当前节点的下个节点
ListNode next = cur.next;
// 2、当前节点指向上个节点(局部反转)
cur.next = pre;
// 3、cur和pre指针后移(先移pre 后移cur,顺序不能反)
pre = cur;
cur = next;
}
return pre;
}
}
234. 回文链表
分析:
大体上分三步:
- 1、先将链表分为两段
- 2、反转第二段链表
- 3、比较两段链表各个节点是否相同?
代码:
class Solution {
public boolean isPalindrome(ListNode head) {
if(head == null) return true;
// 先将链表分为两段
ListNode fast = head;
ListNode slow = head;
while(fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
ListNode newList = slow.next;
slow.next = null;
// 反转第二段链表
ListNode prev = null;
ListNode cur = newList;
while(cur != null) {
ListNode nextNode = cur.next;
cur.next = prev;
prev = cur;
cur = nextNode;
}
// 比较两段链表各个节点是否相同?
while(prev != null) {
if(prev.val != head.val) {
return false;
}
prev = prev.next;
head = head.next;
}
return true;
}
}
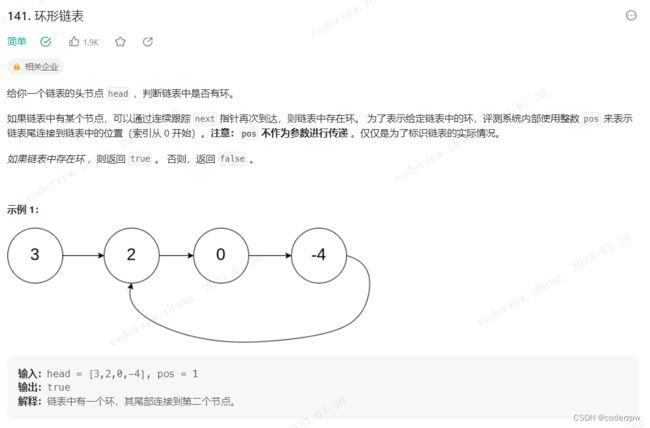
141. 环形链表(基础模板题)
分析:
可以参考我之前总结的这篇文章,很详细【判断单链表是否有环?以及入环节点】
代码:
public class Solution {
public boolean hasCycle(ListNode head) {
if(head == null) return false;
if(head.next == null) return false;
ListNode slow = head.next;
ListNode fast = head.next.next;
while(slow != fast) {
if(fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
}
142. 环形链表 II
分析:
可以参考我之前总结的这篇文章,很详细【判断单链表是否有环?以及入环节点】
代码:
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head == null) return null;
if(head.next == null) return null;
ListNode slow = head.next;
ListNode fast = head.next.next;
while (slow != fast) {
if(fast == null || fast.next == null) {
return null;
}
slow = slow.next;
fast = fast.next.next;
}
slow = head;
while(slow != fast) {
slow = slow.next;
fast = fast.next;
}
return fast;
}
}
21. 合并两个有序链表(模板题)
【21. 合并两个有序链表】
分析:
- 双指针分别指向 list1 和 list2
- 比较list1 和 list2 的指针指向的节点大小,更小者最拼接到新链表末尾,并且指针后移
- 若某一个链表已经遍历完,那么直接将另一个未遍历完的链表连接到新链表的尾部
直接看代码,代码更清晰
代码:
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
// 新链表的虚拟头结点
ListNode head = new ListNode(0);
ListNode cur = head;
// 从list1 和 list2 中取更小者拼接到新链表尾部
while(list1 != null && list2 != null) {
if(list1.val <= list2.val) {
cur.next = list1;
list1 = list1.next;
} else {
cur.next = list2;
list2 = list2.next;
}
cur = cur.next;
}
// 能走到这里,只有有两种情况:1、list1合并完了、list2没合并完 2、list1没合并完、list2合并完了
// 合并list1剩余的元素
if(list1 != null) {
cur.next = list1;
}
// 合并list2剩余的元素
if(list2 != null) {
cur.next = list2;
}
return head.next;
}
}
2. 两数相加
分析:
详细流程可参考代码
总结注意点:
- 常规链表的移动指针,三个移动指针对应三个链表
while(null != head1 || null != head2)循环条件是 || 不是&&(任意一个链表没走完就执行的逻辑)int num1 = null==head1 ? 0 : head1.val当前节点 为null取0,否则取val- 构建进位变量
carry,作用域一定要放到外面;放里面就没法用了 - 考虑最后一步:最后节点遍历完后,判断最后一步运算是否进位了,进位则补1,否则不处理
代码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode head1 = l1; // 移动指针1,指向链表1
ListNode head2 = l2; // 移动指针2,指向链表2
// 构建结果链表
ListNode resHead = new ListNode();
ListNode temp = resHead;// 移动指针3,指向链表3
// 进位值, 默认是0 (作用域一定要是外面)
int carry = 0;
while(null != head1 || null != head2) {
// 为空取0, 否则取val(核心思想)
int num1 = null==head1 ? 0 : head1.val;
int num2 = null==head2 ? 0 : head2.val;
int sum = num1 + num2 + carry;
// 求模取余 获取当前节点值
int curVal = sum % 10;
// 整除获取进位值
carry = sum / 10;
// 构建当前节点
ListNode curNode = new ListNode(curVal);
// 尾插法
temp.next = curNode; temp = curNode;
// 节点后移,只需要考虑不为null的链表即可,因为为null的话我们默认取0, 不会有影响
if(null != head1)
head1 = head1.next;
if(null != head2)
head2 = head2.next;
}
// 最后节点遍历完后,判断最后一步运算是否进位了,进位则补1,否则不处理
if(carry == 1) {
ListNode lastNode = new ListNode(1);
temp.next = lastNode;
}
return resHead.next;
}
}
19. 删除链表的倒数第 N 个结点
分析:
- 算出链表的长度 -
size - 根据
n和size算出待删除节点的前一个节点位置 - 找到待删除节点的前一个节点
- 调用
cur.next = cur.next.next删除目标节点
为了避免处理边界节点,我们可以在头结点前面加一个虚拟头结点dummyHead
代码:
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
int size = 0;
ListNode cur = head;
// 算出链表的长度
while(cur != null) {
size++;
cur = cur.next;
}
// 计算待删除节点 的 前一个位置
int index = size - n;
// 虚拟头结点(避免处理特殊的边界情况)
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
cur = dummyHead;
// 指针指向待删除节点的前一个节点
for(int i=0; i<index; i++) {
cur = cur.next;
}
// 删除目标节点
cur.next = cur.next.next;
return dummyHead.next;
}
}
24. 两两交换链表中的节点
分析:
参考视频讲解:【帮你把链表细节学清楚! | LeetCode:24. 两两交换链表中的节点】
代码:
class Solution {
public ListNode swapPairs(ListNode head) {
if(head == null) return null;
ListNode dummyNode = new ListNode(0);
dummyNode.next = head;
ListNode cur = dummyNode;
while(cur.next != null && cur.next.next != null) {
// 保存下一个节点
ListNode temp1 = cur.next;
// 保存下下下个节点
ListNode temp2 = cur.next.next.next;
// 处理指向关系
cur.next = temp1.next;
cur.next.next = temp1;
temp1.next = temp2;
// cur后移两步
cur = cur.next.next;
}
return dummyNode.next;
}
}
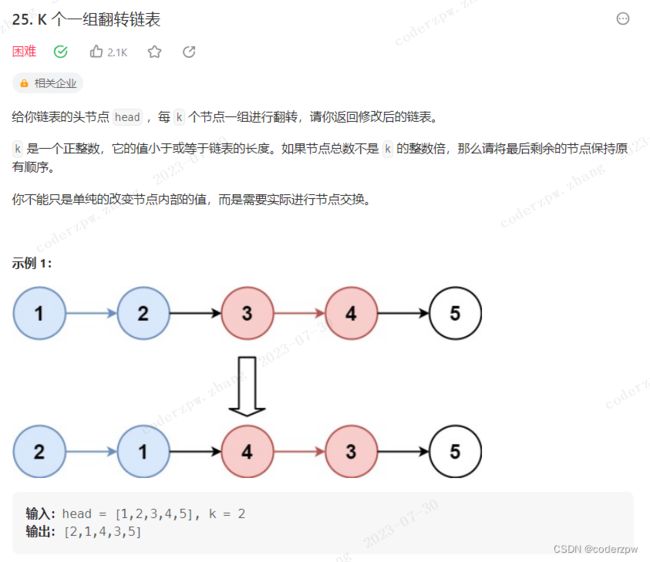
25. K 个一组翻转链表
分析:
参考讲解视频:【【LeetCode 25. K 个一组翻转链表】 每天一题刷起来!C++ 年薪冲冲冲!】
- 先将前 k 个节点组成的链表进行翻转
- 递归处理剩余的链表
代码:
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
// 特殊情况一:【链表为null 或者 k==1, 没必要反转】
if(head == null || k == 1) {
return head;
}
// end 指向当前节点
ListNode end = head;
// 下面这一段代码主要用来判断, 链表长度是否小于k
for(int i=1; i<k && end != null; i++) {
end = end.next;
}
if(end == null) { // 若end为null说明 剩下节点不足k个了,不需要翻转
return head;
}
// 走到此处 [head,end] 其实就是当前需要翻转的k个节点
// 排除完特殊情况 下面就是正常情况了。 此时cur已经指向第k个节点了
// 先保存下一节点(k+1)地址 , 因为接下来要断开 cur与k+1 节点的连接
ListNode nextListHead = end.next;
// 断开k节点 与 k+1节点的连接 因为接下来要单独反转当前组单链表了
end.next = null;
// 反转当前组 单项链表
ListNode newHead = reverse(head); // 翻转之后,之前的head其实就跑到尾部了
// 递归处理剩余剩下的链表,并拼接在之前的head后面(此时的head指针指向的是尾部)
head.next = reverseKGroup(nextListHead, k);
// 返回反转后的新头节点
return newHead;
}
/**
* 翻转单链表
*/
private ListNode reverse(ListNode head) {
ListNode cur = head;
ListNode prev = null;
while(cur != null) {
ListNode nextNode = cur.next;
cur.next = prev;
prev = cur;
cur = nextNode;
}
return prev;
}
}
138. 复制带随机指针的链表
分析:
- 第一次遍历原链表:简单复制新的节点(此时新老节点 仅仅是val相同),遍历的过程中将新、老节点的映射关系存储在
map中 - 第二次遍历原链表:复制链表中 next 、 random的指向关系(依赖map中的映射关系)
代码:
class Solution {
public Node copyRandomList(Node head) {
if(head == null) {
return null;
}
Map<Node, Node> map = new HashMap();
Node cur = head;
// 1、 第一次遍历原链表: 创建对应的新节点 并且对应关系存入到map集合中
while(cur != null) {
// 1.1 创建新节点
Node newNode = new Node(cur.val);
// 2.2 并将 以oldNode为key,newNode为value的方式存入到map中 oldNode:newNode
map.put(cur, newNode);
cur = cur.next;
}
// 2、第一次遍历原链表:进行深拷贝
cur = head;
while(cur != null) {
// 2.1 复制对应next节点
map.get(cur).next = map.get(cur.next);
// 2.2 复制对应random节点
map.get(cur).random = map.get(cur.random);
cur = cur.next;
}
return map.get(head);
}
}
148. 排序链表
分析:
最简单的做法就是将所有节点放到集合中,然后对集合进行排序(任意排序算法都可以),这里可参考【八大排序算法】
了解排序算法的,会发现归并排序处理链表是非常舒服的,尤其是合并阶段
该题我使用的就是链表版的归并排序,数组版的归并排序可以参考:【归并排序】
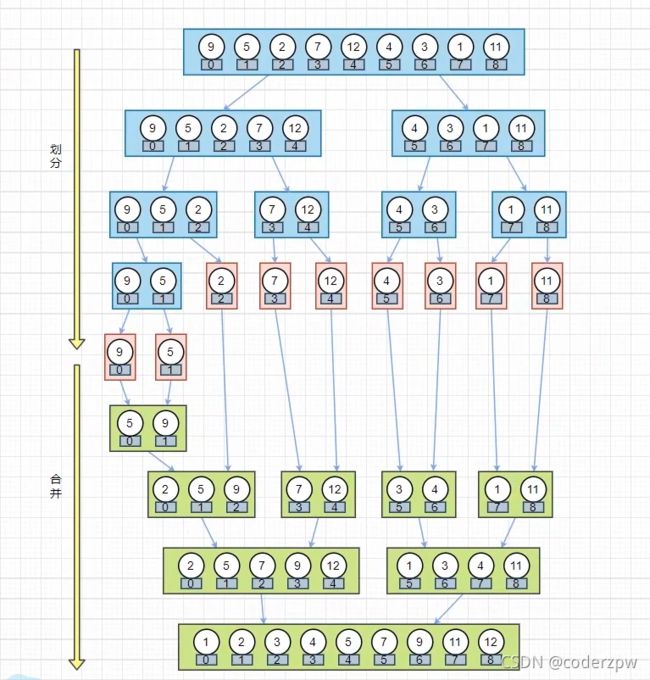
归并排序主要分两个阶段:
- 分治:将待排序列二分,一直向下划分,直到只有一个元素为止(只有一个元素相当于已排序)
- 合并:将已排序的两个子序列合并为一个新的有序序列(主要逻辑)
该题我拆分了三个小方法:
【获取链表中心元素】
在【LeetCode刷题总结 - 剑指offer系列 - 持续更新】这篇文章中有总结过,当存在偶数个节点时,怎么获取中心左侧的元素?怎么获取中心右侧的元素?
该题中我们要获取的是中心左侧的元素,因为后面我们要断开链表就需要靠左的元素执行 node.next = null
/**
* 返回中心节点
* 若节点个数为偶数,则返回中心左边的节点,例如[1,2,3,4],最终返回2
*/
public ListNode getMiddle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
【合并两个有序的链表】
/**
* 归并:将两个有序的链表 合并为一个链表
*/
public ListNode merge(ListNode left, ListNode right) {
// 虚拟头节点
ListNode head = new ListNode(0);
ListNode cur = head;
// 合并(左链表、右链表都存在未合并的元素)
while(left != null && right != null) {
if(left.val <= right.val) {
cur.next = left;
left = left.next;
} else {
cur.next = right;
right = right.next;
}
cur = cur.next;
}
// 能走到这里,只有有两种情况:1、左边合并完了、右边没合并完 2、左边没合并完、右边合并完了
// 合并左链表剩余的元素
if(left != null) {
cur.next = left;
}
// 合并右链表剩余的元素
if(right != null) {
cur.next = right;
}
return head.next;
}
【归并排序整体框架】
public ListNode sort(ListNode head) {
// 终止条件,只有一个元素就不必再排序了
if(head != null && head.next == null) {
return head;
}
// 获取中心节点
ListNode middle = getMiddle(head);
// 从中心断开,left为做链表,right为右链表
ListNode right = middle.next;
middle.next = null;
ListNode left = head;
// 递归划分处理左半段
ListNode sortedLeft = sort(left);
// 递归划分处理右半段
ListNode sortedRight = sort(right);
// 将划分后的排序合并(排序的主要逻辑在这个方法里)
return merge(sortedLeft, sortedRight);
}
代码:
class Solution {
public ListNode sortList(ListNode head) {
if(head == null) {
return null;
}
return sort(head);
}
public ListNode sort(ListNode head) {
// 终止条件,只有一个元素就不必再排序了
if(head != null && head.next == null) {
return head;
}
// 获取中心节点
ListNode middle = getMiddle(head);
// 从中心断开,left为做链表,right为右链表
ListNode right = middle.next;
middle.next = null;
ListNode left = head;
// 递归划分处理左半段
ListNode sortedLeft = sort(left);
// 递归划分处理右半段
ListNode sortedRight = sort(right);
// 将划分后的排序合并(排序的主要逻辑在这个方法里)
return merge(sortedLeft, sortedRight);
}
/**
* 归并:将两个有序的链表 合并为一个链表
*/
public ListNode merge(ListNode left, ListNode right) {
// 虚拟头节点
ListNode head = new ListNode(0);
ListNode cur = head;
// 合并(左链表、右链表都存在未合并的元素)
while(left != null && right != null) {
if(left.val <= right.val) {
cur.next = left;
left = left.next;
} else {
cur.next = right;
right = right.next;
}
cur = cur.next;
}
// 能走到这里,只有有两种情况:1、左边合并完了、右边没合并完 2、左边没合并完、右边合并完了
// 合并左链表剩余的元素
if(left != null) {
cur.next = left;
}
// 合并右链表剩余的元素
if(right != null) {
cur.next = right;
}
return head.next;
}
/**
* 返回中心节点
* 若节点个数为偶数,则返回中心左边的节点,例如[1,2,3,4],最终返回2
*/
public ListNode getMiddle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
}
23. 合并 K 个升序链表
分析:
还是归并排序的思路。
其实归并排序的本质就是,将两个有序的序列合并为一个有序的序列。归并排序是先将长序列 分成无数个小的子序列,其实就是为了得到有序的序列,因为当子序列长度为1时,就可以看做有序的序列了,紧接着在二二合并
该题其实就是给了我们已经排序好的子序列,然后让我们二二合并,而为了提高效率,我们可以参考归并排序使用分治的思想,时间复杂度(nlogk)
代码:
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists == null || lists.length==0) {
return null;
}
return partition(lists, 0, lists.length-1);
}
/**
* 本质上还是归并排序的框架
*/
public ListNode partition(ListNode[] lists, int left, int right) {
// 终止条件,只有一个链表就没必要再合并了
if(left == right) {
return lists[left];
}
int mid = (left + right) >> 1;
// 递归处理左边
ListNode sortedLeft = partition(lists, left, mid);
// 递归处理右边
ListNode sortedRight = partition(lists, mid+1, right);
// 归并
return merge(sortedLeft, sortedRight);
}
/**
* 归并:将两个有序的链表 合并为一个链表
*/
public ListNode merge(ListNode left, ListNode right) {
// 虚拟头节点
ListNode head = new ListNode(0);
ListNode cur = head;
// 合并(左链表、右链表都存在未合并的元素)
while(left != null && right != null) {
if(left.val <= right.val) {
cur.next = left;
left = left.next;
} else {
cur.next = right;
right = right.next;
}
cur = cur.next;
}
// 能走到这里,只有有两种情况:1、左边合并完了、右边没合并完 2、左边没合并完、右边合并完了
// 合并左链表剩余的元素
if(left != null) {
cur.next = left;
}
// 合并右链表剩余的元素
if(right != null) {
cur.next = right;
}
return head.next;
}
}
二叉树
94. 二叉树的中序遍历
代码:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList();
dfs(root, res);
return res;
}
public void dfs(TreeNode root, List<Integer> res) {
if(root == null) return;
dfs(root.left, res);
res.add(root.val);
dfs(root.right, res);
}
}
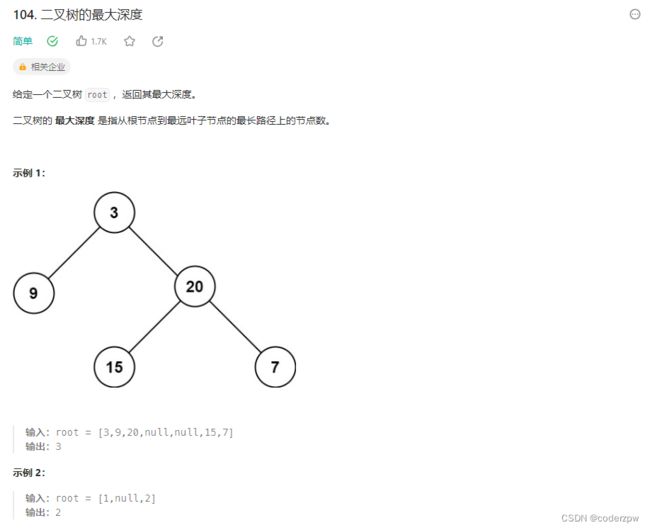
104. 二叉树的最大深度
代码:
class Solution {
public int maxDepth(TreeNode root) {
return getDepth(root);
}
public int getDepth(TreeNode root) {
if(root == null) return 0;
int leftDepth = getDepth(root.left);
int rightDepth = getDepth(root.right);
return Math.max(leftDepth, rightDepth) + 1;
}
}
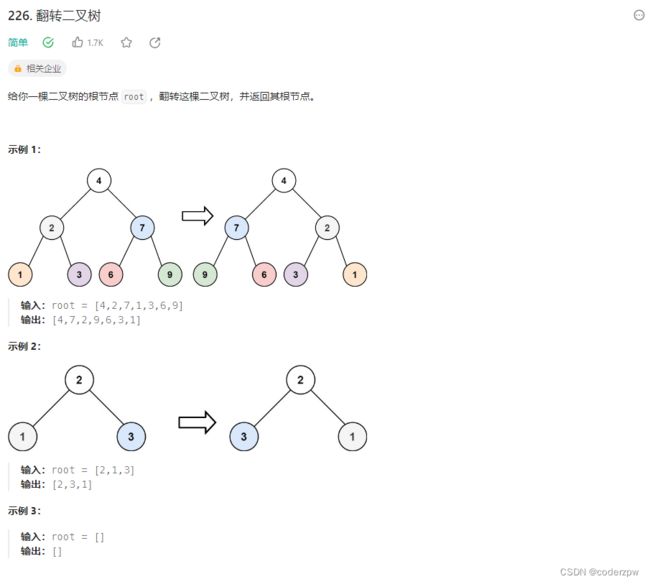
226. 翻转二叉树
代码:
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null) return null;
swap(root);
invertTree(root.left);
invertTree(root.right);
return root;
}
public void swap(TreeNode root) {
if(root == null) return;
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
}
101. 对称二叉树
分析:
- 这里是把根节点的左右子树当做两棵树
- 然后比较这两棵树是否对称
比较两棵树是否相同的主要代码:
boolean leftIsSame = isSame(root1.left, root2.left);
boolean rightIsSame = isSame(root1.right, root2.right);
比较两棵树是否对称的主要代码:
// 判断对称的外侧,即 左树的左孩子 与 右树的右孩子
boolean outFlag = symmetric(root1.left, root2.right);
// 判断对称的内侧,即 左树的右孩子 与 右树的左孩子
boolean inFlag = symmetric(root1.right, root2.left);
代码:
class Solution {
public boolean isSymmetric(TreeNode root) {
return symmetric(root.left, root.right);
}
public boolean symmetric(TreeNode root1, TreeNode root2) {
if(root1 == null && root2 == null) {
return true;
}
if(root1 == null || root2 == null) {
return false;
}
if(root1.val != root2.val) {
return false;
}
// 判断对称的外侧,即 左树的左孩子 与 右树的右孩子
boolean outFlag = symmetric(root1.left, root2.right);
// 判断对称的内侧,即 左树的右孩子 与 右树的左孩子
boolean inFlag = symmetric(root1.right, root2.left);
return outFlag && inFlag;
}
}
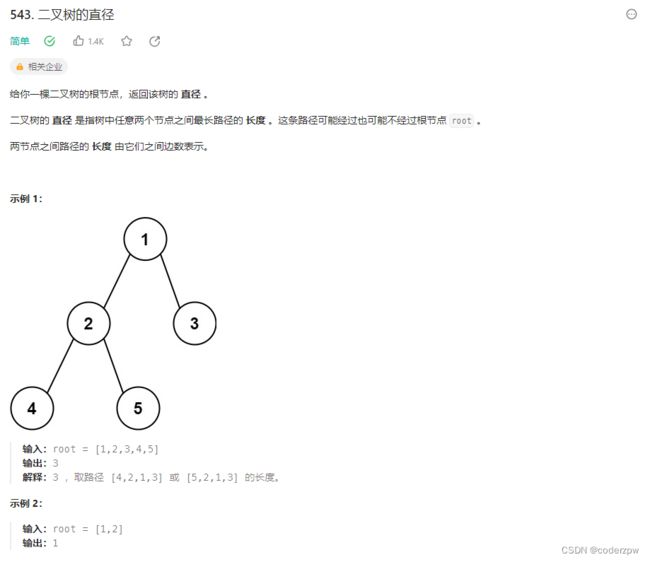
543. 二叉树的直径
分析:
- 使用一个变量维护最大直径
- 在求二叉树深度的基础上,更新 最大直径
- 直径求法:
左子树深度+右子树深度+1
代码:
class Solution {
int maxLength = 0;
public int diameterOfBinaryTree(TreeNode root) {
getDepth(root);
return maxLength - 1;
}
public int getDepth(TreeNode root) {
if(root == null) return 0;
int lDepth = getDepth(root.left);
int rDepth = getDepth(root.right);
maxLength = Math.max(maxLength, lDepth + rDepth + 1);
return Math.max(lDepth, rDepth) + 1;
}
}
102. 二叉树的层序遍历
分析:
一样的模板套路
代码:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) {
return new ArrayList();
}
List<List<Integer>> res = new ArrayList();
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()) {
int len = queue.size();
List<Integer> list = new ArrayList();
for(int i=0; i<len; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null) {
queue.offer(node.left);
}
if(node.right != null) {
queue.offer(node.right);
}
}
res.add(list);
}
return res;
}
}
108. 将有序数组转换为二叉搜索树
分析:
当看到有序数组,第一印象想到二分
当看到二叉树,第一印象想到中序遍历,但是这题是构造二叉树,因此用不到中序遍历
- 每次都取数组中心元素作为根节点,那么左、右子树的节点个数绝对值相差一定<=1
- 左、右子树其实是规模更小的相同问题,顺其自然想到递归分治的思想
- 分别处理左、右子数组,直到
left > right为止
代码:
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return dfs(nums, 0, nums.length - 1);
}
public TreeNode dfs(int[] nums, int left, int right) {
if(left > right) {
return null;
}
int mid = (left + right) >> 1;
TreeNode root = new TreeNode(nums[mid]);
root.left = dfs(nums, left, mid - 1);
root.right = dfs(nums, mid + 1, right);
return root;
}
}
98. 验证二叉搜索树
分析:
- 使用一个变量维护上一个节点的值
- 中序遍历,若当前节点>前一个节点大,则为false
代码:
class Solution {
long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
boolean leftFlag = isValidBST(root.left);
if(root.val <= prev) return false;
prev = root.val;
boolean rightFlag = isValidBST(root.right);
return leftFlag && rightFlag;
}
}
剑指 Offer 54. 二叉搜索树的第k大节点
【剑指 Offer 54. 二叉搜索树的第k大节点】
![]()
分析:
- 对于二叉搜索树,中序遍历最终是有序的
代码:
class Solution {
private List<Integer> res = new ArrayList();
public int kthLargest(TreeNode root, int k) {
dfs(root, k);
return res.get(k-1);
}
public void dfs(TreeNode root, int k) {
if(root == null) {
return;
}
// 若res的大小是k,则不用再遍历了
if(res.size() == k) {
return;
}
// 中序遍历搜索树,最终是有序序列
dfs(root.right, k);
res.add(root.val);
dfs(root.left, k);
}
}
199. 二叉树的右视图
分析:
层次遍历,取每一层的末尾节点
代码:
class Solution {
public List<Integer> rightSideView(TreeNode root) {
if(root == null) {
return new ArrayList();
}
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
List<Integer> res = new ArrayList();
while(!queue.isEmpty()) {
int length = queue.size();
for(int i=0; i<length; i++) {
TreeNode node = queue.poll();
if(node.left != null) {
queue.offer(node.left);
}
if(node.right != null) {
queue.offer(node.right);
}
if(i == length-1) {
res.add(node.val);
}
}
}
return res;
}
}
114. 二叉树展开为链表
分析:
参考视频:【【LeetCode 每日一题】114. 二叉树展开为链表 | 手写图解版思路 + 代码讲解】
代码:
class Solution {
public void flatten(TreeNode root) {
TreeNode cur = root;
// 遍历二叉树
while(cur != null) {
// 若左子树不为空,则特殊处理
if(cur.left != null) {
// 1、 找到左子树中 最右侧的节点 p
TreeNode p = cur.left;
while(p.right != null) {
p = p.right;
}
// 2、改变指向关系
p.right = cur.right;
cur.right = cur.left;
cur.left = null;
}
// 指针到右孩子
cur = cur.right;
}
}
}
105. 从前序与中序遍历序列构造二叉树
分析:
上面【分治算法-系列】的【剑指 Offer 07. 重建二叉树】
代码:
class Solution {
int[] preorder;
int[] inorder;
// 存储中序遍历 对应值的下标
private HashMap<Integer, Integer> inorderMap = new HashMap();
public TreeNode buildTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
this.inorder = inorder;
for(int i=0; i<inorder.length; i++) {
inorderMap.put(inorder[i], i);
}
return build(0, preorder.length-1, 0, inorder.length-1);
}
public TreeNode build(int left1, int right1, int left2, int right2) {
if(left1>right1 || left2>right2) {
return null;
}
int rootVal = preorder[left1];
TreeNode root = new TreeNode(rootVal);
int idx = inorderMap.get(rootVal);
int leftTreeSize = idx - left2; // 左子树大小
int rightTreeSize = right2 - idx; // 右子树大小
// 构建左孩子
root.left = build(left1+1, left1+leftTreeSize, left2, left2+leftTreeSize-1);
// 构建右孩子
root.right = build(left1+leftTreeSize+1, right1, idx+1, right2);
return root;
}
}
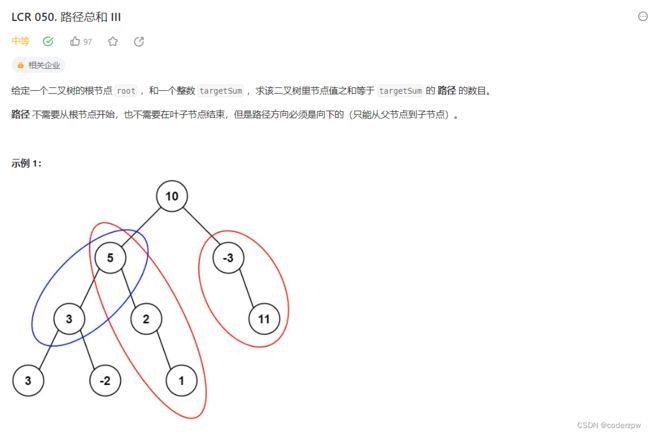
LCR 050. 路径总和 III
分析:
与上面两题不同的几点:
- 这次“路径”的定义,不一定是从根节点到叶子节点(因此我们要遍历整棵树的每个节点,再以该节点为根调用dfs深度优先,并且目标条件不再判断是否为叶子节点)
- 这次节点值 可以是负数、0、正数(因此我们再找到某条路径后,不能return,还要再往深入走,因为节点值可能为负数)
解题步骤:
- 遍历该树的每个节点
- 以每个节点为根,分别调用dfs深度搜索,找到目标路径并累加到计数器
代码:
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
int count = 0; // 计数器,记录路径总数
// 遍历该树的每个节点,再调用dfs(这一步主要是遍历的作用)
public int FindPath (TreeNode root, int sum) {
// 套路
if(root == null) return count;
// 执行当前节点的逻辑 这里是 dfs(root,sum);
dfs(root,sum);
// 递归遍历 该节点的左右子树
FindPath(root.left, sum);
FindPath(root.right, sum);
// 最终返回计数器 count
return count;
}
// 深度遍历 统计路径条数
void dfs(TreeNode root, int sum) {
// 套路模板 先判空
if(root == null) return;
// 执行当前节点的正常逻辑,这里是:sum-=val,以及找寻目标 sum==0
sum -= root.val;
if(sum == 0) // 这里与前面的题不同的是 不用判断 左右节点为null 因为路径定义不一定非是叶子节点
count++; // 这里为什么不return呢? 因为节点可以为负数,继续往深处走,可能还满足
// 递归深度搜索左右孩子
dfs(root.left, sum);
dfs(root.right, sum);
}
}
心得:
- 一般先遍历每个节点再将每个节点看做树根操作的,都可以使用两个递归配合操作。先遍历树, 再对每个节点分别操作。
236. 二叉树的最近公共祖先
分析:
上面已经总结过该题:【剑指 Offer 68 - II. 二叉树的最近公共祖先】
代码:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) {
return null;
}
return dfs(root, p, q);
}
// 【后续遍历】的特点:可以把最终返回的节点 通过递归一直往上推
public TreeNode dfs(TreeNode root, TreeNode p, TreeNode q) {
// 当前节点为null,则肯定找不到,直接返回null
if(root == null) {
return null;
}
// 找到了p 或者 q,则向上返回
if(root == p || root == q) {
return root;
}
// 【左】
TreeNode left = dfs(root.left, p, q);
// 【右】
TreeNode right = dfs(root.right, p, q);
// 【中】
if(left != null && right != null) {
// 若左、右子树都找到了,则当前节点就是最近公共节点
return root;
} else if (left != null && right == null) {
// 左树找到了,但右树没找到,则返回left结果
return left;
} else if(right != null && left == null) {
// 右树找到了,但左树没找到,则返回right结果
return right;
} else {
// 都没找到,则向上返回null
return null;
}
}
}
图论
200. 岛屿数量
分析:
- 遍历所有网格,遇到陆地点,则以该点开始深度优先遍历
- 遍历过的点要打上标记(避免后序重复遍历)
代码:
class Solution {
public int numIslands(char[][] grid) {
int count = 0;
for(int i=0; i<grid.length; i++) {
for(int j=0; j<grid[0].length; j++) {
// 遇到陆地
if(grid[i][j] == '1') {
dfs(grid, i, j);
count++;
}
}
}
return count;
}
public void dfs(char[][] grid, int x, int y) {
// 边界条件
if(!inArea(grid, x, y)) {
return;
}
// 不是岛屿不处理
if(grid[x][y] != '1') {
return;
}
// 遍历过要加上标记
grid[x][y] = '2';
dfs(grid, x-1, y); // 上
dfs(grid, x+1, y); // 下
dfs(grid, x, y-1); // 左
dfs(grid, x, y+1); // 右
}
public boolean inArea(char[][] grid, int x, int y) {
return x >= 0 && x < grid.length && y >=0 && y < grid[0].length;
}
}
994. 腐烂的橘子
分析:
广度优先
参考题解:【理清思路:为什么用 BFS,以及如何写 BFS 代码(Java/Python)】
代码:
class Solution {
public int orangesRotting(int[][] grid) {
Queue<int[]> queue = new LinkedList();
int m = grid.length;
int n = grid[0].length;
int fresh = 0;
int time = 0;
// 遍历橘子
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
if(grid[i][j] == 1) { // 新鲜橘子,则fresh++
fresh++;
} else if (grid[i][j] == 2) { // 将腐烂的橘子加入队列中
queue.offer(new int[]{i, j});
}
}
}
// 没有新鲜的,直接返回0
if(fresh == 0) return 0;
// 广度优先
while(!queue.isEmpty() && fresh > 0) { // 必须满足,新鲜的数量>0, 否则就没必要遍历了
int len = queue.size();
time++;
for(int i=0; i<len; i++) {
int[] badOrange = queue.poll();
int x = badOrange[0];
int y = badOrange[1];
// 上, 只腐蚀新鲜的,坏的在之前已经遍历过了
if(x-1 >= 0 && grid[x-1][y] == 1) {
grid[x-1][y] = 2; // 腐蚀
fresh--;
queue.offer(new int[]{x-1, y});
}
// 下
if(x+1 < m && grid[x+1][y] == 1) {
grid[x+1][y] = 2;
fresh--;
queue.offer(new int[]{x+1, y});
}
// 左
if(y-1 >= 0 && grid[x][y-1] == 1) {
grid[x][y-1] = 2;
fresh--;
queue.offer(new int[]{x, y-1});
}
// 右
if(y+1 < n && grid[x][y+1] == 1) {
grid[x][y+1] = 2;
fresh--;
queue.offer(new int[]{x, y+1});
}
}
}
return fresh == 0 ? time : -1;
}
}
207. 课程表
【207. 课程表】
分析:
参考视频:【207. 课程表 Course Schedule 【LeetCode 力扣官方题解】】
参考题解:【「图解」拓扑排序 | 课程表问题】
代码:
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
// 课号和对应的入度
Map<Integer, Integer> inDegreeMap = new HashMap();
for(int i=0; i<numCourses; i++) {
inDegreeMap.put(i, 0);
}
// 依赖关系, 依赖当前课程的后序课程
Map<Integer, List<Integer>> outDegreeCourseMap = new HashMap();
for(int[] arr: prerequisites) {
int prev = arr[1];
int cur = arr[0];
// 更新出度集合列表
if(!outDegreeCourseMap.containsKey(prev)) {
outDegreeCourseMap.put(prev, new ArrayList());
}
outDegreeCourseMap.get(prev).add(cur);
// 更新入度
inDegreeMap.put(cur, inDegreeMap.get(cur) + 1);
}
// BFS,将入度为0(不需要前置课程)的课程放入列表
Queue<Integer> queue = new LinkedList();
for(int key: inDegreeMap.keySet()) {
if(inDegreeMap.get(key) == 0) {
queue.offer(key);
}
}
while(!queue.isEmpty()) {
int cur = queue.poll();
if(!outDegreeCourseMap.containsKey(cur)) {
continue;
}
List<Integer> outDegreeCourse = outDegreeCourseMap.get(cur);
for(int course: outDegreeCourse) {
inDegreeMap.put(course, inDegreeMap.get(course) - 1);
// 入度为0,说该课的前修改已经修完,所以当前课可以修了
if (inDegreeMap.get(course) == 0) {
queue.offer(course);
}
}
}
// 遍历入度, 如果还有课程的入度不为0, 返回fasle
for (int key : inDegreeMap.keySet()) {
if (inDegreeMap.get(key) != 0) {
return false;
}
}
return true;
}
}
208. 实现 Trie (前缀树)
代码:
class Trie {
// 自定义Node节点数据结构
private class Node {
// 词典
Map<Character, Node> dict = new HashMap();
// 是否为终止节点
boolean isEnd = false;
}
// 一棵树的根节点
private Node root;
public Trie() {
// 初始化根节点
root = new Node();
}
public void insert(String word) {
Node cur = this.root;
char[] charArr = word.toCharArray();
for(char ch: charArr) {
Map<Character, Node> dict = cur.dict;
// 若当前词典不存在该字符对应的Node,则为该字符创建Node
if(!dict.containsKey(ch)) {
dict.put(ch, new Node());
}
// 指针下移
cur = dict.get(ch);
}
// 将终止节点的打上终止标记
cur.isEnd = true;
}
public boolean search(String word) {
Node endNode = searchPrefix(word);
// 若终止节点不为空 并且 endNode为true,说明词典中存在目标单词
return endNode != null && endNode.isEnd;
}
public boolean startsWith(String prefix) {
Node endNode = searchPrefix(prefix);
// 若终止节点不为空,说明有目标前缀
return endNode != null;
}
/**
* 搜索目标前缀,并返回最后终止节点
*/
public Node searchPrefix(String prefix) {
// 从根节点出发
Node cur = this.root;
char[] charArr = prefix.toCharArray();
// 遍历搜索字符
for(char ch: charArr) {
Map<Character, Node> dict = cur.dict;
// 若词典节点为null,则说明没有,直接返回null
if(dict.get(ch) == null) {
return null;
}
// 指针下移,继续向下搜索
cur = dict.get(ch);
}
// 最终返回终止节点
return cur;
}
}
回溯
回溯章节建议跟随【代码随想录-回溯】课程学习
真心推荐,卡尔讲的很不错
回溯模板
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
常规回溯题 与 二叉树回溯题的差别
二叉树的回溯整体上确实是回溯的思想,大体思路也差不多。但在处理细节上还是有些不同的,例如【剑指 Offer 34. 二叉树中和为某一值的路径】与【39. 组合总和】相比:
- 二叉树要从根节点处理(每次递归中处理的是当前节点);而常规回溯题一般不处理根节点(每次递归中处理的都是孩子节点,而且是多孩子);因此在处理细节上是有差异的
- 二叉树递归代码:
public void backtracking(TreeNode root, int target, List<Integer> path) {
if(root == null) {
return;
}
// 处理当前节点
target -= root.val;
path.add(root.val);
if(target == 0 && root.left == null && root.right == null) {
res.add(new ArrayList(path));
}
// 处理左右孩子节点
backtracking(root.left, target, path);
backtracking(root.right, target, path);
// 状态重置
target += root.val;
path.remove(path.size() - 1);
}
- 常规回溯递归代码:
public void backtracking(List<Integer> path, int startIndex, int[] candidates, int target) {
// 终止条件
if(target == 0) {
res.add(new ArrayList(path));
return;
}
// for循环处理孩子节点
for(int i=startIndex; i<candidates.length; i++) {
// 剪枝:因为我们事先已经为数组排好序了,越往后数字越大,如果当前数字都已经减到负数了,那后面的就没必要在判断了
if(target - candidates[i] < 0) {
break;
}
target -= candidates[i];
path.add(candidates[i]);
backtracking(path, i, candidates, target);
// 状态重置
target += candidates[i];
path.remove(path.size() - 1);
}
}
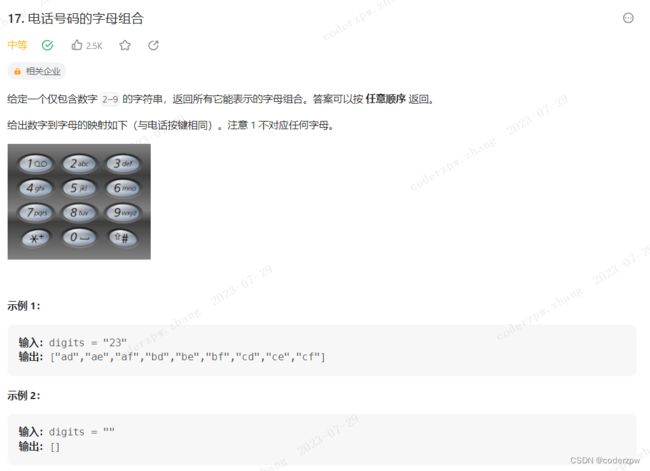
17. 电话号码的字母组合
分析:
套用上面的模板即可,不细讲了
// 删除最后一个字符
sb.deleteCharAt(sb.length() - 1)
代码:
class Solution {
private List<String> res = new ArrayList();
StringBuilder path = new StringBuilder();
private String[] letters = {" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public List<String> letterCombinations(String digits) {
if (digits.length() == 0) {
return new ArrayList();
}
StringBuilder path = new StringBuilder();
backtracking(0, digits);
return res;
}
public void backtracking(int level, String digits) {
// 不合法(终止条件)
if(path.length() == digits.length()) { // 此处也可以写成 level == digits.length() 来做为终止条件
res.add(path.toString()); // 添加到结果集
return;
}
// 找到对应的候选集
int index = digits.charAt(level) - '0';
char[] chars = letters[index].toCharArray();
// 因为每层的可选集都是独立的,因此for循环都可以从0开始(不会重复)
for(int i=0; i<chars.length; i++) {
path.append(chars[i]);
backtracking(level + 1, digits);
path.deleteCharAt(path.length() - 1); // 状态重置
}
}
}
77. 组合
分析:
参考视频:【带你学透回溯算法-组合问题(对应力扣题目:77.组合)| 回溯法精讲!】
可以将这题与上题对比来看
相同点:
- 都是组合问题,路径组合不能重复(例如:234 和 324就是重复的)
不同点:
- 上一题,每层的可选集都不一样。例如,输入“23”,第一层的可选集是“a、b、c”,第二层的可选集是“d、e、f”,因此我们在遍历每层的可选集时,都可以从下标0开始遍历(因为是独立的数据集,所以不会重复)
- 而该题,每层的可选集都是一样(都是[1,n]),但是我们要保证路径元素不能重复,所以在处理for循环时就要注意。下面是模拟回溯的多叉树状态,从左往右、从上到下 可选集的返回都会缩小1。这时我们使用
startIndex来记录下一层搜索的起始位置(for循环的初始下标)
核心代码如下:
for(int i=startIndex; i<=n; i++):从startIndex开始遍历,保证组合路径不会重复
backtracking(temp, i + 1, n, k):使用i+1,保证组合中的元素不会重复
// 从左往右看 因为i本身会自增,且递归函数为backtracking(temp, i + 1, n, k),参数2就是startIndex,因此越往右可选范围越小
// 越往下也是一样,调用backtracking(temp, i + 1, n, k),越往下可选集范围越小
for(int i=startIndex; i<=n; i++) {
temp.add(i);
backtracking(temp, i + 1, n, k); // 核心
temp.remove(temp.size() - 1);
}
代码:
class Solution {
List<List<Integer>> res = new ArrayList();
List<Integer> path = new ArrayList();
public List<List<Integer>> combine(int n, int k) {
backtracking(1, n, k);
return res;
}
public void backtracking(int startIndex, int n, int k) {
// 终止条件
if(path.size() == k) {
res.add(new ArrayList(path));
return;
}
// 遍历 [startIndex, n]
for(int i=startIndex; i<=n; i++) {
path.add(i); // 操作当前节点
backtracking(i + 1, n, k); // 这里是i+1,不要错写成startIndex+1了
path.remove(path.size() - 1); // 状态重置
}
}
}
39. 组合总和
分析:
组合问题,因此我们也需要一个 startIndex 变量作为遍历的起始位置。这样做是为了避免出现重复的组合(例如:234 和 324就是重复的)
但与上题不同在于,该题可以允许组合中的元素重复,因此在调用递归方法时,startIndex就没必要+1了
剪枝:为了提高效率,我们事先对数组进行排序,越往后数字越大,如果加到某个节点已经超过了目标值,那后面的就没必要在判断了,因为加起来和会更大
代码:
class Solution {
List<List<Integer>> res = new ArrayList();
List<Integer> path = new ArrayList();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
// 排序 后后序剪枝做准备
Arrays.sort(candidates);
backtracking(0, candidates, target);
return res;
}
public void backtracking(int startIndex, int[] candidates, int target) {
// 终止条件
if(target == 0) {
res.add(new ArrayList(path));
return;
}
for(int i=startIndex; i<candidates.length; i++) {
// 剪枝:因为我们事先已经为数组排好序了,越往后数字越大,如果当前数字都已经减到负数了,那后面的就没必要在判断了
if(target - candidates[i] < 0) {
break;
}
target -= candidates[i];
path.add(candidates[i]);
backtracking(i, candidates, target);
// 状态重置
target += candidates[i];
path.remove(path.size() - 1);
}
}
}
剑指 Offer 34. 二叉树中和为某一值的路径
分析:
二叉树的回溯整体上确实是回溯的思想,大体思路也差不多。但在处理细节上还是有些不同的,例如和前面组合问题相比:
- 二叉树要从根节点处理(每次递归中处理的是当前节点);而常规回溯题一般不处理根节点(每次递归中处理的都是孩子节点,而且是多孩子);因此在处理细节上是有差异的
- 二叉树代码 :
public void backtracking(TreeNode root, int target, List<Integer> path) {
if(root == null) {
return;
}
// 处理当前节点
target -= root.val;
path.add(root.val);
if(target == 0 && root.left == null && root.right == null) {
res.add(new ArrayList(path));
}
// 处理左右孩子节点
backtracking(root.left, target, path);
backtracking(root.right, target, path);
// 状态重置
target += root.val;
path.remove(path.size() - 1);
}
- 常规回溯代码:
public void backtracking(List<Integer> path, int startIndex, int[] candidates, int target) {
// 终止条件
if(target == 0) {
res.add(new ArrayList(path));
return;
}
// for循环处理孩子节点
for(int i=startIndex; i<candidates.length; i++) {
// 剪枝:因为我们事先已经为数组排好序了,越往后数字越大,如果当前数字都已经减到负数了,那后面的就没必要在判断了
if(target - candidates[i] < 0) {
break;
}
target -= candidates[i];
path.add(candidates[i]);
backtracking(path, i, candidates, target);
// 状态重置
target += candidates[i];
path.remove(path.size() - 1);
}
}
代码:
class Solution {
private List<List<Integer>> res = new ArrayList();
public List<List<Integer>> pathSum(TreeNode root, int target) {
List<Integer> path = new ArrayList();
backtracking(root, target, path);
return res;
}
public void backtracking(TreeNode root, int target, List<Integer> path) {
if(root == null) {
return;
}
// 处理当前节点
target -= root.val;
path.add(root.val);
if(target == 0 && root.left == null && root.right == null) {
res.add(new ArrayList(path));
}
// 递归调用左右子节点
backtracking(root.left, target, path);
backtracking(root.right, target, path);
// 状态重置
target += root.val;
path.remove(path.size() - 1);
}
}
46. 全排列
分析:
因为不是组合问题,所以我们每层遍历时都不用缩小可选的范围,只需要判断当前路径中是否存在该元素即可
代码:
class Solution {
List<List<Integer>> res = new ArrayList();
List<Integer> path = new ArrayList();
public List<List<Integer>> permute(int[] nums) {
backtracking(nums);
return res;
}
public void backtracking(int[] nums) {
if(path.size() == nums.length) {
res.add(new ArrayList(path));
return;
}
for(int i=0; i<nums.length; i++) {
// 若存在重复元素则不添加
if(path.contains(nums[i])) {
continue;
}
path.add(nums[i]);
backtracking(nums);
path.remove(path.size() -1);
}
}
}
47. 全排列 II
分析:
与上题不同,该题中提到序列中可能有重复的元素,因此我们要考虑对排列去重
整体逻辑可参考视频:【代码随想录:回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II】
去重逻辑可参考视频:【代码随想录:回溯算法中的去重,树层去重树枝去重,你弄清楚了没?| LeetCode:40.组合总和II】
我们使用一个used数组来表示某个下标的元素在当前路径中是否被使用过?
核心代码:
/**
* 树层去重操作, 当前前元素 与 前一个元素相同,且前一个元素在当前路径未使用过
* 树层去重:arr[i] == arr[i-1] && used[i-1] == 0
* 树枝去重:arr[i] == arr[i-1] && used[i-1] == 1
*/
if(i > 0 && arr[i] == arr[i-1] && used[i-1] == 0) {
continue;
}
代码:
class Solution {
List<List<Integer>> res = new ArrayList();
List<Integer> path = new ArrayList();
public List<List<Integer>> permuteUnique(int[] nums) {
int[] used = new int[nums.length];
// 对元素排序,方便去重处理
Arrays.sort(nums);
backtracking(nums, used);
return res;
}
public void backtracking(int[] nums, int[] used) {
if(path.size() == nums.length) {
// 错误写法:res.add(path);
// 正确写法:res.add(new ArrayList(path));
res.add(new ArrayList(path));
return;
}
for(int i=0; i<nums.length; i++) {
// 【去重处理】若树层重复,则直接跳过
if(i > 0 && nums[i-1] == nums[i] && used[i-1] == 0) {
continue;
}
// 已使用过则跳过
if(used[i] == 1) {
continue;
}
path.add(nums[i]);
used[i] = 1;
backtracking(nums, used);
used[i] = 0;
path.remove(path.size() - 1);
}
}
}
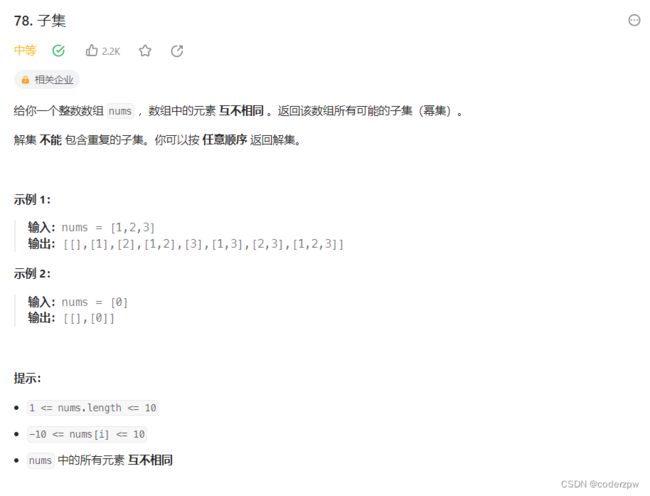
78. 子集
分析:
其实【子集】问题本身就是【组合】问题。
例如:求[1,2,3] 的子集,其实就是求 长度为0、长度为1、长度为2、长度为3 的组合的并集
长度为0的组合:[]
长度为1的组合:[1]、[2]、[3]
长度为2的组合:[1,2]、[1,3]、[2,3]
长度为3的组合:[1,2,3]
代码不同点:
【组合】问题:叶子节点收获结果
【子集】问题:每个节点都是结果
参考视频:【回溯算法解决子集问题,树上节点都是目标集和! | LeetCode:78.子集】
代码:
class Solution {
List<List<Integer>> res = new ArrayList();
List<Integer> path = new ArrayList();
public List<List<Integer>> subsets(int[] nums) {
backtracking(0, nums);
return res;
}
public void backtracking(int startIndex, int[] nums) {
// 每个节点都是结果
res.add(new ArrayList(path));
for(int i=startIndex; i<nums.length; i++) {
path.add(nums[i]);
backtracking(i + 1, nums);
path.remove(path.size() - 1);
}
}
}
51. N 皇后
分析:
参考视频:【这就是传说中的N皇后? 回溯算法安排!| LeetCode:51.N皇后】
参考题解:51. N-Queens:【回溯法经典问题】详解
- 用一个二维数组
chessBoard来记录棋盘的状态 - 每往下深入一行,然后遍历各个列,判断 当前点
chessBoard[row][col]是否有效? - 是否有效判断逻辑:判断当前点
左上方、正上方、右上方是否有皇后,若存在则说明不符合规则 是无效的,就返回false
代码:
class Solution {
List<List<String>> res = new ArrayList();
public List<List<String>> solveNQueens(int n) {
char[][] chessBoard = new char[n][n];
// 初始化棋盘,默认都是'.'
for(char[] chars: chessBoard) {
Arrays.fill(chars, '.');
}
backtracking(chessBoard, n, 0);
return res;
}
public void backtracking(char[][] chessBoard, int n, int row) {
if(row == n) {
res.add(arrayToList(chessBoard));
return;
}
for(int col=0; col<n; col++) {
if(isValid(chessBoard, n, row, col)) {
chessBoard[row][col] = 'Q';
backtracking(chessBoard, n, row + 1);
chessBoard[row][col] = '.';
}
}
}
/**
* 检查 chessBoard[row][col] 的 “正上方”、“左上方”、“右上方” 是否有皇后?
* 存在皇后,说明chessBoard[row][col]是无效的返回false,不存在说明chessBoard[row][col]是有效的,返回true
*/
public boolean isValid(char[][] chessBoard, int n, int row, int col) {
// 检查上方 是否有皇后
for(int i=0; i<row; i++) {
if(chessBoard[i][col] == 'Q') {
return false;
}
}
// 检查左上方 是否有皇后
for(int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) { // 往左上角移动
if(chessBoard[i][j] == 'Q') {
return false;
}
}
// 检查右上方 是否有皇后
for(int i=row-1, j=col+1; i>=0 && j<n; i--, j++) { // 往右上角移动
if(chessBoard[i][j] == 'Q') {
return false;
}
}
return true;
}
/**
* 二维字符数组 -> 字符串集合
*/
public List arrayToList(char[][] chessBoard) {
List<String> list = new ArrayList();
for(char[] chars: chessBoard) {
list.add(new String(chars));
}
return list;
}
}
22. 括号生成
分析:
参考题解:【虽然不是最秀的,但至少能让你看得懂!】
还是常规的回溯法,一样的配方
- 该题 可以看做 从 数组
[ '(' , ')' ]中进行2*n次排列(该数组仅有左括号和有括号2个元素)
- 需要满足一定条件才能拼接到
path路径中(剪枝)- 充要条件:
左括号数量<=n并且右括号数量<=左括号数量 - 代码:
left <= n && right <= left
- 充要条件:
代码:
class Solution {
List<String> res = new ArrayList();
StringBuilder path = new StringBuilder();
public List<String> generateParenthesis(int n) {
backtracking(0, 0, n);
return res;
}
/**
* left、right 分别指左右括号的数量
*/
public void backtracking(int left, int right, int n) {
// 终止条件
if(path.length() == n * 2) {
res.add(path.toString());
return;
}
// 递归处理子孩子(因为只有左、右两种括号,因此就只有两个孩子)
if(isValid(left+1, right, n)) { // 追加一个“左括号”
path.append('(');
backtracking(left + 1, right, n);
path.deleteCharAt(path.length() - 1);
}
if(isValid(left, right+1, n)) { // 追加一个“右括号”
path.append(')');
backtracking(left, right + 1, n);
path.deleteCharAt(path.length() - 1);
}
}
/**
* 判断是否有效?有两个充要条件:
* 1、leftCount 必须 小于等于 n
* 2、leftCount 必须 大于等于 rightCount
*/
public boolean isValid(int leftCount, int rightCount, int n) {
return leftCount <= n && leftCount >= rightCount;
}
}
131. 分割回文串
分析:
该题难点是如何遍历所有的切割方式?(难点)
解决的上面的问题后,接下来就是判断切割的字符串是否是回文的?(判断回文是比较简单的)
其实切割方式的遍历,类似于组合问题。下面是回溯对应的树形结构:
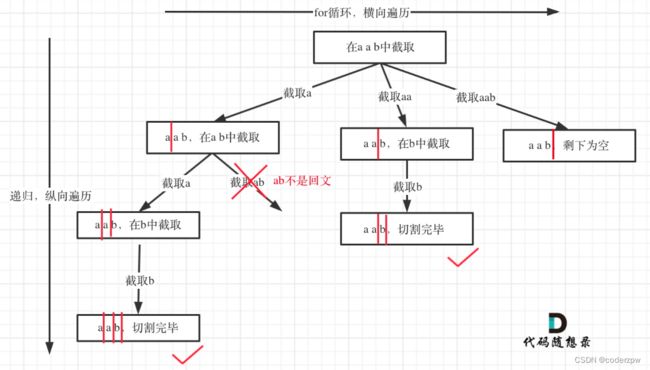
详细题解可参考:【「代码随想录」带你学透回溯算法!131. 分割回文串】
视频讲解可参考:【带你学透回溯算法-分割回文串(对应力扣题目:131.分割回文串)| 回溯法精讲!】
该题理解起来还是比较复杂的,可以多看几遍视频和题解
代码:
初始版本:
class Solution {
List<List<String>> res = new ArrayList();
List<String> path = new ArrayList();
public List<List<String>> partition(String s) {
backtracking(s, 0);
return res;
}
public void backtracking(String s, int startIndex) {
// 分割线到达最后,说明已经遍历完一种切割方式
if(startIndex == s.length()) {
res.add(new ArrayList(path));
return;
}
for(int i=startIndex; i<s.length(); i++) {
// 只有满足[startIndex, i]是回文串,才能添加到path中
if(isPalindrome(s, startIndex, i)) {
String str = s.substring(startIndex, i + 1);
path.add(str);
} else {
continue;
}
// 递归继续找下一个分割线
backtracking(s, i + 1);
path.remove(path.size() - 1);
}
}
// 判断是否回文
public boolean isPalindrome(String s, int left, int right) {
char[] charArr = s.toCharArray();
while(left <= right) {
if(charArr[left] != charArr[right]) {
return false;
}
left++;
right--;
}
return true;
}
}
优化方法:
将【[i,j]段是否回文?】的状态预存在二维数组中
class Solution {
List<List<String>> res = new ArrayList();
List<String> path = new ArrayList();
boolean[][] isPalindrome;
public List<List<String>> partition(String s) {
int len = s.length();
isPalindrome = new boolean[len][len];
// 将[i,j]段是否回文?的状态预先存到二维数组-isPalindrome中
prepare(s);
// 回溯遍历所有切割情况,并填充结果集
backtracking(s, 0);
return res;
}
public void backtracking(String s, int startIndex) {
// 分割线到达最后,说明已经遍历完一种切割方式
if(startIndex == s.length()) {
res.add(new ArrayList(path));
return;
}
for(int i=startIndex; i<s.length(); i++) {
// 只有满足[startIndex, i]是回文串,才能添加到path中
if(isPalindrome[startIndex][i]) {
String str = s.substring(startIndex, i + 1);
path.add(str);
} else {
continue;
}
// 递归继续找下一个分割线
backtracking(s, i + 1);
path.remove(path.size() - 1);
}
}
// 预处理判断 [i,j]是否回文,将判断结果预存在isPalindrome数组中
public void prepare(String s) {
for(int i=0; i<s.length(); i++) {
extendFromCenter(s, i, i); // aba
extendFromCenter(s, i, i + 1); // abba
}
}
// 中心扩展法
public void extendFromCenter(String s, int left, int right) {
char[] charArr = s.toCharArray();
int len = charArr.length;
while(left >= 0 && right < len && charArr[left] == charArr[right]) {
// 满足回文条件,打标记
isPalindrome[left][right] = true;
// 向外扩展
left--;
right++;
}
}
}
二分查找
模板
参考视频:【最清楚的二分查找!LeetCode34题:在排序数组中查找元素的第一个和最后一】
参考文章:【二分查找算法及其变种详解】
正常搜索目标值:
public int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
变种一:搜索值为target的第一个下标:
/**
* 找第一个目标值
*/
public int binarySearchFirst(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] == target) {
// 下面两种情况,都说明是最左侧的target
if (mid == 0 || nums[mid - 1] != target)
return mid;
// 否则继续向左半区间查找
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
变种二:搜索值为target的最后一个下标:
/**
* 找最后一个目标值
*/
public int binarySearchLast(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] == target) {
// 下面两种情况,都说明是最右侧的target
if (mid == nums.length-1 || nums[mid + 1] != target)
return mid;
// 否则继续向右半区间查找
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
变种三:查找第一个大于等于 给定值的元素
/**
* 第一个 >=target 的下标
*/
public int binarySearch3(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] >= target) {
if(mid == 0 || nums[mid - 1] < target)
return mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
变种四:查找最后一个小于等于给定值的元素
/**
* 最后一个 <=target 的下标
*/
public int binarySearch4(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] <= target) {
if(mid == nums.length-1 || nums[mid + 1] > target)
return mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
变种五:查找第一个大于 给定值的元素
/**
* 第一个 >target 的下标
*/
public int binarySearch5(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] > target) {
if(mid == 0 || nums[mid - 1] <= target)
return mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
变种六:查找最后一个小于给定值的元素
/**
* 最后一个
public int binarySearch6(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] < target) {
if(mid == nums.length-1 || nums[mid + 1] >= target)
return mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
总结注意点
【注意点一】:若[left,right] 对应 [0,length-1],当代码中需要mid与相邻元素比较时,要和nums[mid+1]比较,如果和num[mid-1]比较,则nums[mid-1]可能会下标越界
- 若数组只有一个元素,其实
nums[mid+1]也会越界。因此只有一个元素时要单独当做边界条件处理 - 若数组只有两个元素,则
mid = (0+1)/2 = 0,那么nums[mid-1]就会越界,nums[mid+1]则不会越界
35. 搜索插入位置
分析:
该题是个模板题
/**
* 二分查找
*/
public int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = (left + right) >> 1; // 等价于 (left + right) / 2
if(nums[mid] == target) {
return mid;
}
if(nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return left;
}
代码:
class Solution {
public int searchInsert(int[] nums, int target) {
return binarySearch(nums, target);
}
/**
* 二分查找
*/
public int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = (left + right) >> 1; // 等价于 (left + right) / 2
if(nums[mid] == target) {
return mid;
}
if(nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return left;
}
}
74. 搜索二维矩阵
分析:
首先题中说明:
每一行都按照从左到右递增的顺序排序
每一列都按照从上到下递增的顺序排序。
那么一看数据是有序的, 那么我们肯定第一时间想到二分查找法。但在着整个二维数组中好像没法直接使用二分查找,但是我们可以使用二分查找的思想。
二分查找思想: 每一轮比较首先获取一个特殊值,然后让目标值与该值进行比较,每次比较都能排除一些数据进而缩小搜索的范围。
解决该题我们用的方法和二叉查找法类似,也是每次都取一个特殊值与目标值比较,每轮都排除一部分数据进而缩小数据的查找范围

B站上讲解视频:
https://www.bilibili.com/video/BV12J411i7A6
https://www.bilibili.com/video/BV1Tt411F7YD?spm_id_from=333.999.0.0
代码:
class Solution {
public boolean searchMatrix(int[][] array, int target) {
// 套路模板 先判空
if(array.length == 0) return false;
// row表示有几行,col表示有几列。
int row = array.length;
int col = array[0].length;
// 我们取右上角的值
int x = 0; int y = col - 1;
// 不断排除一列或者一行,不断缩小范围
while(x <= row-1 && y >= 0) {
if(target > array[x][y]) {
// 排除头一行的数据
x++;
}else if (target < array[x][y]) {
// 排除后一列的数据
y--;
}else {
return true;
}
}
// 若判处完所有数据仍没有找目标值 该值不存在
return false;
}
}
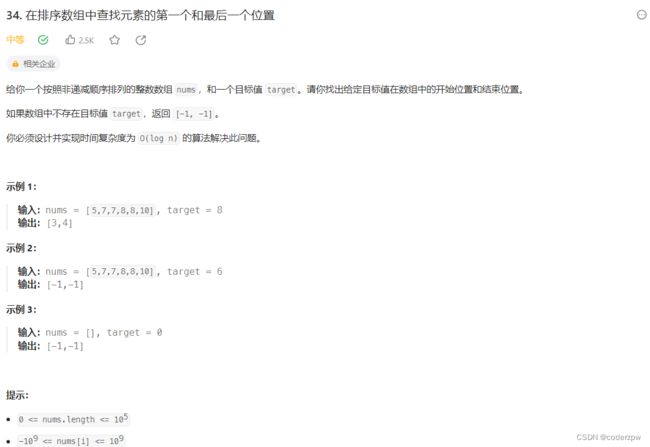
34. 在排序数组中查找元素的第一个和最后一个位置
分析:
分别获取 第一个目标值 和 最后一个目标值
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] res = new int[2];
res[0] = binarySearchFirst(nums, target);
res[1] = binarySearchLast(nums, target);
return res;
}
public int binarySearchFirst(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] == target) {
// 下面两种情况,都说明是最左侧的target
if (mid == 0 || nums[mid - 1] != target)
return mid;
// 否则继续向左半区间查找
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
/**
* 找最后一个目标值
*/
public int binarySearchLast(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + ((right - left) >> 1);
if(nums[mid] == target) {
// 下面两种情况,都说明是最右侧的target
if (mid == nums.length-1 || nums[mid + 1] != target)
return mid;
// 否则继续向右半区间查找
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
}
JZ11 旋转数组的最小数字(存在重复值)
【JZ11 旋转数组的最小数字】
分析:
参考视频:【剑指Offer.6.旋转数组的最小数字】
序列可被分为两部分递增序列, 第一部分的最小值 >= 第二部分的最最大值
若 min下标的值 > 最右侧的值 ,则说明 min下标处于第一部分,而最小值在第二部分的范围内,因此我们就可以排除 min及左侧的所有数据了,最小值在 [min+1,right] 的范围内
若 min下标的值 < 最右侧的值, 则说明min下标所处第二部分,那么最小值在 [left,min]的范围内
若min下标的值 == 最右侧的值,而对于这种情况,又一种特殊情况,如下图:

直接说结论,若 min下标的值 == 最右侧的值, 则直接 right-- 即可,右指针后移
while循环的条件是 left < right,当left == right时,其实就只有一个数据了,该数据就是最小,最终直接返回array[left] 或者 array[right]
代码:
import java.util.ArrayList;
public class Solution {
public int minNumberInRotateArray(int [] array) {
// 套路模板,先判空
if(array.length == 0) return -1;
return erfen(array, 0, array.length-1);
}
public int erfen(int[] array, int left, int right) {
int min = 0;
while(left < right) { // 因为当left==right时,其实就是我们要找的目标值,因此这里条件是left
min = (left + right) >> 1; // 等同于(left+right)/2
// 因为没有目标值,因此每次都是 中间下标值 与 最右侧的值进行比较
if(array[min] > array[right]) { // 此情况说明min处于 第一部分的范围
left = min + 1;
}else if(array[min] < array[right]) { // 此情况说明min处于 第二部分范围 因为可能是最小值 因此right不再是min+1
right = min;
}else { // 若min 等于 最右侧的值, 直接right往左移一步即可,right--
right--;
}
}
// 最后 left=right 就是我们要找的最小值
return array[left];
}
}
153. 寻找旋转排序数组中的最小值(不包含重复值)
分析:
与上题不同,该题数组元素是不重复的,因此判断逻辑中不需要判断 nums[mid] == nums[right]这种情况
代码:
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while(left < right) {
int mid = (left + right) >> 1;
if(nums[mid] > nums[right]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left];
}
}
33. 搜索旋转排序数组
分析:
* 假设turningPointIdx为转折点下标:此时我们知道这两段递增序列范围(若数组本身就没有翻转,则还是一个段[0, nums.length-1]),分别是:
* 第一段:[0,turningPointIdx-1]
* 第二段:[turningPointIdx, nums.length-1]
* "第一段元素" > "第二段元素"
一共分三步:
- 找到转折点下标
- 判断
target所在的标有序区间turningPointIdx == 0,说明nums本身就是有序的,并没有翻转。则target还在[0, nums.length-1]内target >= nums[0],说明target在[0,turningPointIdx-1]target < nums[0],说明target在[turningPointIdx, nums.length-1]
- 在有序区间内进行二分查找
代码:
class Solution {
/**
* 假设turningPointIdx为转折点下标:此时我们知道这两段递增序列范围(若数组本身就没有翻转,则还是一个段[0, nums.length-1]),分别是:
* 第一段:[0,turningPointIdx-1]
* 第二段:[turningPointIdx, nums.length-1]
* "第一段元素" > "第二段元素"
*/
public int search(int[] nums, int target) {
// 【一、找到转折点下标】
int turningPointIdx = getTurningPoint(nums);
// 【二、target与nums[0]比较,判断target在 第一段 还是 第二段?】
// turningPointIdx == 0,说明nums本身就是有序的,并没有翻转
int left, right;
if(turningPointIdx == 0) {
left = 0;
right = nums.length - 1;
} else if (target >= nums[0]) {
// target在第一段
left = 0;
right = turningPointIdx - 1;
} else {
// target在第二段
left = turningPointIdx;
right = nums.length - 1;
}
// 【三、在有序范围内进行二分查找】
return binarySearch(nums, left, right, target);
}
/**
* 寻找旋转点的下标(就是找到转折数组的最小值)
* 若没有旋转(本身是有序的),则最终返回的下标肯定是0
*/
public int getTurningPoint(int[] nums) {
int left = 0;
int right = nums.length - 1;
while(left < right) {
int mid = (left + right) >> 1;
if(nums[mid] > nums[right]) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
/**
* 在有序数组中进行二分查找
*/
public int binarySearch(int[] nums, int left, int right, int target) {
while(left <= right) {
int mid = (left + right) >> 1;
if(nums[mid] == target) {
return mid;
}
if(nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
}
栈
20. 有效的括号
分析:
不算太难哈,直接看代码
代码:
class Solution {
public boolean isValid(String s) {
char[] charArr = s.toCharArray();
Stack<Character> stack = new Stack();
for(char ch: charArr) {
if(ch == '(') {
stack.push(')');
} else if (ch == '{') {
stack.push('}');
} else if (ch == '[') {
stack.push(']');
} else {
if(stack.isEmpty() || ch != stack.pop()) {
return false;
}
}
}
return stack.isEmpty();
}
}
155. 最小栈
分析:
解题步骤:
为了解决要求栈的最小值而且要保证时间复杂度较低的要求,我们需要还需要一个栈区存某一状态下的最小值。因此 这里一共使用两个栈空间,一个栈用于存放普通数据,另一个则用于存放最小值数据
// 该栈就是正常的栈,添加什么数据就压入什么数据
Stack<Integer> normalStack = new Stack();
// 该栈存入的是 相对于normalStack来说 某一状态(状态可以理解为栈的大小)下的最小值(栈顶存最小值)
Stack<Integer> minStack = new Stack();
push方法:
- 首先数据存入到normalStack 中。
- 紧接着该存最小值了。如果minStack是空的,那么直接将插入值压入minStack即可。
- 如果minStack不为空,那么就取出栈顶元素(前个状态的最小值)与插入值进行比较,如果插入值更小就将插入值压入minStack;如果还是前一个状态的最小值更小 就将前个状态的最小值再压入minStack,因为minStack的栈顶元素始终存的都是当前状态的最小值(当前状态可以理解为normalStack当前的深度、大小)
pop方法:
normalStack.pop();
minStack.pop();
两个栈弹出栈顶元素即可(必须都要弹出,要保证minStack与normalStack的状态一致)
top方法:
normalStack.peek();
获取normalStack的栈顶元素即可
min方法:
minStack.peek();
获取minStack的栈顶元素即可
代码:
class MinStack {
// 实际存储数据的栈
Stack<Integer> stack = new Stack();
// 辅助栈,存储当前状态的最小值
Stack<Integer> stack1 = new Stack();
public MinStack() {
}
public void push(int val) {
stack.push(val);
if(stack1.isEmpty()) {
stack1.push(val);
} else {
stack1.push(Math.min(stack1.peek(), val));
}
}
public void pop() {
stack.pop();
stack1.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return stack1.peek();
}
}
739. 每日温度
【739. 每日温度】
分析:
单调栈 维护 还未找到后面更高温度的日期
参考视频:【单调栈,你该了解的,这里都讲了!LeetCode:739.每日温度】
代码:
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
// 单调递增栈,存放还未找到最近最高温度的日期,存放的是下标
Stack<Integer> stack = new Stack();
// 存放待返回的结果
int[] ret = new int[temperatures.length];
stack.push(0);
// 遍历温度表
for(int i=1; i<temperatures.length; i++) {
int cur = temperatures[i];
// 若栈顶温度 小于 当天温度,则说明当天温度 相对于 栈顶元素来说,就是最近的更高温度
while(!stack.isEmpty() && temperatures[stack.peek()] < cur) {
// 已经为栈顶元素找到了 最近的最高温度,则没必要放到栈中了
int popedIdx = stack.pop();
// 记录天数差
ret[popedIdx] = i - popedIdx;
}
stack.push(i);
}
// 最后stack不为空,则说明stack中的元素 后面找不到更高温度的日期
while(!stack.isEmpty()) {
int popedIdx = stack.pop();
ret[popedIdx] = 0;
}
return ret;
}
}
42. 接雨水
分析:
参考视频:【单调栈,经典来袭!LeetCode:42.接雨水】
建议先做上一题
- 找到
较低点的前一个较大值和后一个较大值,则可以算较低点相对于前、后两个较大点所接的雨水(横向求解,水平求解) - 维护一个
单调栈(存储下标),若当前值大于栈顶元素,则栈顶元素就是较低点,栈顶第二个元素就是较低点的前一个较大点,当前值就是较低点的下一个较大点
代码:
class Solution {
public int trap(int[] height) {
// stack维护一个单调栈(非递减),存储下标
Stack<Integer> stack = new Stack();
// 记录接雨水的总数
int sum = 0;
for(int i=0; i<height.length; i++) {
int cur = height[i];
// 若栈顶元素 小于 当前值则弹出(表示当前值是栈顶元素的后续第一个较大者)
while(!stack.isEmpty() && height[stack.peek()] < cur) {
// nextHeight:下个较大值(下标)
int nextHeight = i;
// mid:就是中间点(下标)
int mid = stack.pop();
if(stack.isEmpty()) { // 若为空 则直接跳过,不处理
break;
}
// preHeight:前一个较大值(下标)
int preHeight = stack.peek();
// 高度差
int diffY = Math.min(height[preHeight], height[nextHeight]) - height[mid];
// 宽度差
int diffX = nextHeight - preHeight - 1;
// 面积累计
sum += diffX * diffY;
}
stack.push(i);
}
return sum;
}
}
堆
数组中的第K个最大元素
分析:
方法一:使用大小为k的小根堆 来维护最大的前k个数
- 先往小根堆中添加k个元素
- 后序的元素都跟小根堆的堆顶元素(最小值)比较,若大于 堆顶元素(最小值),则替换。否则不处理
方法二:
利用快速排序的思想,不断的构造轴点元素,当轴点坐标为K时,那么arr的topK就是最小的前K个数
可以参考:【排序算法之快速排序】
代码:
解法一:
class Solution {
public int findKthLargest(int[] nums, int k) {
// 小根堆
PriorityQueue<Integer> minHeap = new PriorityQueue<>((a, b) -> a - b);
int len = nums.length;
for(int i=0; i<k; i++) {
minHeap.offer(nums[i]);
}
for(int i=k; i<len; i++) {
if(nums[i] > minHeap.peek()) {
minHeap.poll();
minHeap.offer(nums[i]);
}
}
return minHeap.peek();
}
}
解法二:
class Solution {
public int findKthLargest(int[] nums, int k) {
quickSort(nums, 0, nums.length - 1, k - 1);
return nums[k - 1];
}
public void quickSort(int[] nums, int left, int right, int k) {
if(left >= right) {
return;
}
int povitIdx = povit(nums, left, right);
if(povitIdx == k) {
return;
}
if(povitIdx < k) {
quickSort(nums, povitIdx + 1, right, k);
} else {
quickSort(nums, left, povitIdx - 1, k);
}
}
public int povit(int[] nums, int left, int right) {
int temp = nums[left];
while(left < right) {
while(left < right && nums[right] <= temp) {
right--;
}
if(left < right) {
nums[left] = nums[right];
left++;
}
while(left < right && nums[left] >= temp) {
left++;
}
if(left < right) {
nums[right] = nums[left];
}
if(left == right) {
nums[left] = temp;
}
}
return left;
}
}
347. 前 K 个高频元素
分析:
其实本质上与上一题一样
- 首先使用map来存储各个数字出现的频率,key为数字,value为对应频率。
- 使用小根堆来维护频率最大的k个数
- 遍历map的所有key(即数字),并在小根堆中过滤
分析:
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// map用于维护nums中数字出现的频率
Map<Integer, Integer> map = new HashMap();
for(int item: nums) {
if(map.containsKey(item)) {
map.put(item, map.get(item) + 1);
} else {
map.put(item, 1);
}
}
// 创建最小堆,根据map中的频率比较
PriorityQueue<Integer> minHeap = new PriorityQueue<>((n1, n2) -> map.get(n1) - map.get(n2));
// 遍历map的key,并从小根堆中过滤
for(int key: map.keySet()) {
if(minHeap.size() < k) {
minHeap.offer(key);
} else {
if(map.get(key) > map.get(minHeap.peek())) {
minHeap.poll();
minHeap.offer(key);
}
}
}
// 将小根堆中的元素添加到结果集中
int[] res = new int[k];
for(int i=0; i<k; i++) {
res[i] = minHeap.poll();
}
return res;
}
}
295. 数据流的中位数
分析:
解题思路:
B站上视频讲解:https://www.bilibili.com/video/BV1J5411J7yj?spm_id_from=333.788.top_right_bar_window_history.content.click
https://www.bilibili.com/video/BV1hi4y1b7z5?spm_id_from=333.788.top_right_bar_window_history.content.click
有多种解法,你可以使用插入排序的写法(可以利用前面序列是有序的特性),这种方式我不写了。
接下来说另一种,用一个大根堆 和 一个小跟堆 来实现
- 左边的数据 使用 大根堆
- 右边的数据 使用 小跟堆
其实这个图是有问题的。其实我们不能保证左边和右边的数据是递增有序的。
但是我们要保证:
左侧大根堆的堆顶元素要满足两点:- 大于左侧的所有元素(大根堆性质就是如此,不需要我们来处理)
- 同时小于右侧的所有元素(需要我们自己去维护这个关系)
右侧小根堆的堆顶元素要满足两点:- 小于右侧的所有元素(小根堆性质就是如此,不需要我们来处理)
- 同时大于左侧的所有元素(需要我们自己去维护这个关系)
- 左右两侧数据数量要均衡,我是这样处理的:
- 当整体数量为偶数,
左侧个数=右侧个数 - 当整体数量为奇数,
右侧数量>左侧数量(相差1)
- 当整体数量为偶数,
- 左侧的元素 都比 右侧的元素小(这样一来 大根堆堆顶就是中位数 或者 两个堆顶的平均值是中位数 )
代码:
class MedianFinder {
// 统计数据流的个数
private int count;
// 维护左侧的大根堆(维护左侧序列)
PriorityQueue<Integer> maxHead = new PriorityQueue(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
// 维护右侧的小根堆(维护右侧序列)
PriorityQueue<Integer> minHead = new PriorityQueue();
public MedianFinder() {
}
public void addNum(int num) {
if(count % 2 == 0) { // 偶数
/**
* 最终添加在右侧序列
* 1、首先将数据添加到左侧的大根堆
* 2、然后将左侧的最大值添加到右侧的小根堆中(最终元素数量增加的是右侧元素)
*/
/**
* 其实1、2 两步可以理解为是一种【过滤操作】,有两个目的:
* 目的1:最终右侧序列新增
* 目的2:最终添加到右侧序列的元素 保证要 大于左侧的所有元素(因此就有了 minHead.offer(maxHead.poll())操作)
*/
maxHead.offer(num);
minHead.offer(maxHead.poll()); // 最终添加在右侧序列
} else { // 道理同上,只是过滤的方向不一样
minHead.offer(num);
maxHead.offer(minHead.poll()); // 最终添加在左侧序列
}
count++;
}
public double findMedian() {
if(count == 0) {
return 0;
}
return count % 2 == 0 ? (maxHead.peek() + minHead.peek()) / 2.0 : minHead.peek();
}
}
贪心算法
55. 跳跃游戏
分析:
参考视频:【LeetCode_55_跳跃游戏】
代码:
class Solution {
public boolean canJump(int[] nums) {
// 最远可到达的下标,默认是0
int farthestArrivalIndex = 0;
int len = nums.length;
for(int i=0; i<len; i++) {
if(farthestArrivalIndex < i) { // 说明不能到达i下标
return false;
}
// 更新最远可到达的下标
farthestArrivalIndex = Math.max(farthestArrivalIndex, i + nums[i]);
}
// 能走到这里说明,能走完
return true;
}
}
45. 跳跃游戏 II
分析:
参考题解:【【跳跃游戏 II】别想那么多,就挨着跳吧 II】
代码:
class Solution {
public int jump(int[] nums) {
int len = nums.length;
if(len == 1) { // 长度为1, 则不用跳,直接返回0
return 0;
}
// 步数
int step = 1;
// 【当前跳】 覆盖的范围
int range = nums[0];
// 【下一跳】 能到达的最远下标。初始值给0
int farthestArrivalIndex = 0;
for(int i=1; i<len; i++) {
// 若【当前跳】范围超过 len-1, 则直接返回step
if(range >= len - 1) {
return step;
}
// 更新 【下一跳】的最远下标
farthestArrivalIndex = Math.max(farthestArrivalIndex, i + nums[i]);
// 若到达【当前跳】的范围边界,则步数增加。新的开始:更新【当前跳】的覆盖范围
if(i == range) {
step++;
range = farthestArrivalIndex;
}
}
return step;
}
}
763. 划分字母区间
分析:
参考视频讲解:【贪心算法,寻找最远的出现位置! LeetCode:763.划分字母区间】
代码:
class Solution {
public List<Integer> partitionLabels(String s) {
List<Integer> res = new ArrayList();
char[] charArr = s.toCharArray();
int len = charArr.length;
// 记录每个字符 最远的下标位置
Map<Character, Integer> map = new HashMap();
for(int i=0; i<len; i++) {
map.put(charArr[i], i);
}
// 记录当前段 的 起始位置
int start = 0;
// 记录当前段 的 末尾位置
int end = 0;
for(int i=0; i<len; i++) {
char ch = charArr[i];
end = Math.max(end, map.get(ch));
if(i == end) {
res.add(end - start + 1);
start = i + 1;
}
}
return res;
}
}
动态规划
70. 爬楼梯
分析:
因为可以爬1级或者2级 ,因此最后一爬,要么从n-1级台阶 要么从n-2级台阶 爬到n级,因此 爬到n级台阶的爬法总和 = 爬到n-1级的爬法和 + 爬到n-2级的爬法和 。 dp[i]表示爬到i级台阶的爬法总和。 状态转移方程为: dp[i] = dp[i-1] + dp[i-2] 其实和斐波那契数列差不多
代码:
class Solution {
public int climbStairs(int n) {
if(n == 1) return 1;
if(n == 2) return 2;
int[] dp = new int[n+1];
dp[1] = 1; dp[2] = 2;
for(int i=3; i<=n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
}
118. 杨辉三角
分析:
类似于 打印三角形数据。两层for循环进行打印。
代码更清晰
代码:
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList();
// 两层for循环 打印三角形
for(int i=0; i<numRows; i++) {
List<Integer> list = new ArrayList();
for(int j=0; j<=i; j++) {
// 当j==0 或者 j==i,说明是三角形的两个侧边,直接赋值为1
if(j == 0 || j == i) {
list.add(1);
continue;
}
// 拿到上一层的数值
List<Integer> upLine = res.get(i-1);
// 根据上一层数值计算当前值
int val = upLine.get(j - 1) + upLine.get(j);
list.add(val);
}
res.add(list);
}
return res;
}
}
322. 零钱兑换
分析:
参考视频:【腾讯二面笔试题~零钱兑换】
若【爬楼梯】的题改成:
每次可爬coins[0]、coins[1] … coins[length-1]个台阶,问最少跳多少次能跳到amount?
其实就和这题一样了
若这题改成:
求兑换零钱的方法总数
其实就变成了【爬楼梯】的进阶版了
定义dp[n]为:兑换n元钱,最少需要的硬币数
dp[n]的状态 来源于 dp[n-coins[i]],因此
dp[n] = min {
dp[n] = dp[n - coins[0]] + 1
dp[n] = dp[n - coins[1]] + 1
dp[n] = dp[n - coins[2]] + 1
...
dp[n] = dp[n - coins[length-1]] + 1
}
有点类似于【剑指 Offer 60. n个骰子的点数】这题
代码:
class Solution {
public int coinChange(int[] coins, int amount) {
if(amount == 0) {
return 0;
}
/**
* 零钱最小值是1,因此amount最多换amount个硬币。
* 为了考虑换不到零钱的情况,我们这里初始值设置为amount+1。最后dp[n] 和 amount+1比较,若仍等于amount+1,则说明n换不到零钱,最终返回-1
*/
// dp[n]定义:兑换amount最少的兑换次数
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
// 当amount为0时,则兑换方法为0
dp[0] = 0;
// 遍历amount(类似于遍历背包容量)
for(int i=1; i<=amount; i++) {
// 遍历金币(类似遍历物品)
for(int j=0; j<coins.length; j++) {
// 若当前金币大于总钱数,则直接continue
if(coins[j] > i) {
continue;
}
// 算出新值:1 + dp[i - coins[j]]
int newVal = 1 + dp[i - coins[j]];
// 更新dp[i]的最小值
dp[i] = Math.min(newVal, dp[i]);
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}
}
279. 完全平方数
分析:
该题其实与【322. 零钱兑换】基本一致。
整数n我们可以理解为总钱数1、4、9...等这些完全平方和我们可以理解为金币
不同点:
- 完全平方和有1(1元的金币),因此肯定能找到零钱(该题我们不需要考虑找不到零钱的情况),因此初始化dp都为n即可
- 遍历完全平方和(遍历金币)是这样的
(int j=1; j*j<=i; j++)
代码:
class Solution {
public int numSquares(int n) {
int[] dp = new int[n+1];
Arrays.fill(dp, n);
dp[0] = 0;
for(int i=1; i<=n; i++) {
for(int j=1; j*j<=i; j++) {
int newVal = 1 + dp[i - j*j];
dp[i] = Math.min(dp[i], newVal);
}
}
return dp[n];
}
}
139. 单词拆分
分析:
类似于完全背包
- 整个
字符串s可以看做是背包,词典可看做是物品,不过这个背包必须按照一定的顺序才能填充 - 两层
for循环。第一层遍历s长度(遍历背包容量);第二层遍历,截取 j到i之间的字符串判断是否在词典中?
步骤:
dp[n]定义:前n个字符组成的字符串是否能被wordDict拼接成功(从1开始)- 若 词典包含
[j,i)并且dp[j]==true,则说明[0,i)可被词典拼接
参考视频:【动态规划之完全背包,你的背包如何装满?| LeetCode:139.单词拆分】
代码:
lass Solution {
public boolean wordBreak(String s, List<String> wordDict) {
int len = s.length();
// dp[n]定义为:前n个字符组成的字符串是否能被wordDict拼接成功(从1开始)
boolean[] dp = new boolean[len+1];
// dp[0]初始为true(没什么特殊含义)
dp[0] = true;
for(int i=1; i<=len; i++) {
for(int j=0; j<i; j++) {
// 词典包含[j,i) 并且 dp[j] 为true
if(wordDict.contains(s.substring(j, i)) && dp[j]) {
dp[i] = true;
}
}
}
return dp[len];
}
}
300. 最长递增子序列
【300. 最长递增子序列】
![]()
分析:
参考视频:https://www.bilibili.com/video/BV19b4y1R7K3?spm_id_from=333.1007.top_right_bar_window_custom_collection.content.click
代码:
class Solution {
public int lengthOfLIS(int[] nums) {
// 用于最大返回值
int res = 1;
int len = nums.length;
// dp数组的含义: 以nums[i]结尾的最长递增子序列的长度(必须包含nums[i])
int[] dp = new int[len];
Arrays.fill(dp, 1);
for(int i=1; i<len; i++) { // 外层循环填dp[i]的值
for(int j=0; j<i; j++) { // 内层循环 遍历nums[i]前面的元素
// 如果前面的值小于当前值 才能满足升序
if(nums[j] < nums[i]) {
int newVal = dp[j] + 1;
dp[i] = Math.max(dp[i], newVal);
}
}
// 从以[0,len)结尾的子序列中找到 最长的一个
res = Math.max(res, dp[i]);
}
/**
* 错误写法:return dp[len-1]
* 原因:最终的结果并非一定以len-1结尾的(而是整个nums子序列),因此最终结果并非dp[len-1]
*/
return res;
}
}
和最大子数组
分析:
技巧:像这种最大、最小 的 子数组、子序列,我们在定义动态数组时,大多数这样定义:dp[i] = 以下标i 值为结尾的 子数组 或者 子序列
- 遍历
nums,填写dp数组 dp[i]以nums[i]结尾;因为dp[i-1]可能小于零,因此不能直接写成dp[i] = dp[i-1]+nums[i],而是dp[i] = Math.max(nums[i], dp[i-1] + nums[i])- 同时全局更新最大和
maxSum = Math.max(maxSum, dp[i])
代码:
class Solution {
public int maxSales(int[] nums) {
int maxSum = nums[0];
int len = nums.length;
int[] dp = new int[len];
dp[0] = nums[0];
for(int i=1; i<len; i++) {
// 当 dp[i-1]小于0,dp[i]=nums[i]
dp[i] = Math.max(nums[i], dp[i-1] + nums[i]);
maxSum = Math.max(maxSum, dp[i]);
}
return maxSum;
}
}
152. 乘积最大子数组
分析:
参考视频:【2022-每天一题-乘积最大子数组】
和【和最大子数组】类似。但又有所不同
- 求最大和:
dp[i] = Math.max(nums[i], dp[i-1] + nums[i]) 即可 - 求最大积:
- 错误写法:
dp[i] = Math.max(nums[i], dp[i-1] * nums[i])。因为乘积有个特点,若当前值为负数,则乘以前面最小值才是最大乘积的。因此我们在处理时,最大乘积、最小乘积 两种情况都要考虑到,最终拿两种情况的最大值 - 正确写法:
dpMax[i] = Math.max(nums[i], Math.max(dpMax[i-1] * nums[i], dpMin[i-1] * nums[i]))
- 错误写法:
代码:
class Solution {
public int maxProduct(int[] nums) {
int len = nums.length;
int[] dpMax = new int[len];
int[] dpMin = new int[len];
dpMax[0] = nums[0];
dpMin[0] = nums[0];
int maxProduct = nums[0];
for(int i=1; i<len; i++) {
// 因为不知道dp[i-1]的正负,因此使用 Math.max(dpMax[i-1] * nums[i], dpMin[i-1] * nums[i]) 求二者最大
dpMax[i] = Math.max(nums[i], Math.max(dpMax[i-1] * nums[i], dpMin[i-1] * nums[i]));
// 因为在求dpMax时需要用到 dpMin, 因此我们要一直维护dpMin。维护方法同上
dpMin[i] = Math.min(nums[i], Math.min(dpMax[i-1] * nums[i], dpMin[i-1] * nums[i]));
// 更新最大乘积
maxProduct = Math.max(maxProduct, dpMax[i]);
}
return maxProduct;
}
}
416. 分割等和子集
分析:
原问题 等价于 判断是否存在nums的子集的和为sum/2?(子集元素不能重复)(sum为数组元素和,且sum必须为偶数)
元素不能重复,因此属于0-1背包问题,建议先学习【0-1背包问题】
代码备注比较详细,可直接参考代码理解
参考视频:
【带你学透0-1背包问题】
【带你学透0-1背包问题-之滚动数组】
【动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集】
参考题解:
【「代码随想录」帮你把0-1背包学个通透!(附背包完整攻略)】
代码:
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int item: nums) {
sum += item;
}
// 若为奇数,肯定不能等分
if(sum % 2 != 0) {
return false;
}
int target = sum / 2;
// 判断是否存在nums的子集的和为target?(子集元素不能重复,因此属于0-1背包问题)
// 背包容量为target
// 物品集为nums
/**
* 一维数组写法(滚动数组)
* 1、最外层遍历 物品
* 2、最内层遍历 背包容量,且必须为倒序
*/
int len = nums.length;
// dp[j]含义:容量为j的背包,最大能装的物品容量
int[] dp = new int[target + 1];
for(int i=0; i<len; i++) { // 遍历物品
for(int j=target; j>0; j--) { // 遍历背包容量
if(j < nums[i]) { // 装不下 直接跳过
break;
}
// 因为 “能装的物品容量” <= “背包容量”, 所以这里取【最大值】最终通过 “dp[j] == j” 巧妙地判断容量为j的背包是否能刚好装满?
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// 当 “容量为target的背包” 最大能装的 “物品总容量为target” 时, 说明背包target恰好装满(若dp[target] == target,则说明恰好装满)
return dp[target] == target;
}
}
打家劫舍系列
198. 打家劫舍
分析:
参考视频:【动态规划,偷不偷这个房间呢?| LeetCode:198.打家劫舍】
dp[n]定义为:考虑第n间房,所能偷的最大值 【但不一定要偷第n间,只是考虑到第n间】(n从0开始)
- 对于第i间来说,有两种选择:1.偷第i间、2.不偷第i间
- 1、偷第
i间房:则不能偷第i-1间房屋,也就不能考虑第n-1间房。则此时value = nums[i] + dp[i-2] - 2、不偷第
i间房:则可以考虑偷第i-1间。则此时value = dp[i-1]
- 1、偷第
- 最终取两种情况的最大值,因此
dp[i] = Math.max(nums[i] + dp[i-2], dp[i-1])
初始化dp:
若只有一间房子肯定要偷第一间,因此dp[0] = nums[0]
有两个房间,不能两个都偷,因此偷最大值,因此 dp[1] = Math.max(nums[0], nums[1])
代码:
class Solution {
public int rob(int[] nums) {
int len = nums.length;
// 只有一个,则肯定偷这一个
if(len == 1) {
return nums[0];
}
// 有两个,则偷最大值
if(len == 2) {
return Math.max(nums[0], nums[1]);
}
// dp[n]定义为:考虑第n间房,所能偷的最大值 【但不一定要偷第n间,只是考虑到第n间】(n从0开始)
int[] dp = new int[len];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for(int i=2; i<len; i++) {
/**
* 有两种选择:1.偷第i间、2.不偷第i间
* 1、偷第i间房:则不能偷第i-1间房屋,也就不能考虑第n-1间房。则此时 value = nums[i] + dp[i-2]
* 2、不偷第i间房:则可以考虑偷第i-1间。则此时 value = dp[i-1]
* 最终取两种情况的最大值,因此 dp[i] = Math.max(nums[i] + dp[i-2], dp[i-1])
*/
dp[i] = Math.max(nums[i] + dp[i-2], dp[i-1]);
}
return dp[len-1];
}
}
213. 打家劫舍 II
分析:
环状排列 意味着第一个房子和最后一个房子中 只能选择一个偷窃(要么不考虑第一个,要么不考虑最后一个),因此可以把此 环状排列房间 问题约化为 两个 单排排列房间 子问题,
- 不考虑第一个房子,数组范围
[1, len) - 不考虑最后一个房子,数组范围
[0, len-1)
最终求两种情况的最大值(最优解)
代码:
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if(len == 1) {
return nums[0];
}
/**
* 因为是环形的,因此第一个和最后一个不能同时偷。所以我们分成两种情况:
* 1、不偷第一个
* 2、不偷最后一个
*/
// 情况一
int robCase1 = myRob(Arrays.copyOfRange(nums, 1, len));
// 情况二
int robCase2 = myRob(Arrays.copyOfRange(nums, 0, len - 1));
// 取最大值
return Math.max(robCase1, robCase2);
}
/**
* 打家劫舍1
*/
public int myRob(int[] nums) {
int len = nums.length;
if(len == 1) {
return nums[0];
}
int[] dp = new int[len];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for(int i=2; i<len; i++) {
dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);
}
return dp[len-1];
}
}
337. 打家劫舍 III
分析:
参考视频讲解:【动态规划,房间连成树了,偷不偷呢?| LeetCode:337.打家劫舍3】
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
int[] res = robTree(root);
return Math.max(res[0], res[1]);
}
public int[] robTree(TreeNode root) {
// res[0]:不偷当前节点的最优值
// res[1]:偷当前节点的最优值
int[] res = new int[2];
if(root == null) {
// 节点为null时,res[0]、res[1]均为0
return res;
}
int[] left = robTree(root.left);
int[] right = robTree(root.right);
// 不偷当前节点:则可以考虑孩子节点。至于到底偷不偷一定是选一个最大的
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
// 偷当前节点:不可以偷孩子节点
res[1] = root.val + left[0] + right[0];
return res;
}
}
多维动态规划
62. 不同路径
分析:
有点像【爬台阶】,到达某点的路径 = 到达上面的路径 + 到达左边的路径
二维版的【爬台阶】
代码:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// 初始化上边界
for(int i=0; i<n; i++) {
dp[0][i] = 1;
}
// 初始化下边界
for(int j=0; j<m; j++) {
dp[j][0] = 1;
}
for(int i=1; i<m; i++) {
for(int j=1; j<n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}
63. 不同路径 II
分析:
有点像【爬台阶】,到达某点的路径 = 到达上面的路径 + 到达左边的路径
不同点:
- 该题是二维的
- 存在障碍物,若某点是障碍物则到达该点的路径为0
- 初始化边界时要注意,若中间遇到障碍物,则后序的点不可能再被到达,因此dp为0
代码:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
/**
* 初始化第一行。
* 只能 → 从左到右,因此如果中遇见障碍物,后面就走不到了,因此obstacleGrid[0][i]==0写在for循环的条件中,若不满足则终止for循环
* 那么后面的则不能被设置为1,最终就是0,表示到达该点的路径为0
*/
for(int i=0; i<n && obstacleGrid[0][i]==0; i++) {
// 等于0,则说明不是障碍物,可以走
dp[0][i] = 1;
}
// 初始化第一列。只能↓ 从上到下,同上
for(int i=0; i<m && obstacleGrid[i][0]==0; i++) {
// 等于0,则说明不是障碍物,可以走
dp[i][0] = 1;
}
for(int i=1; i<m; i++) {
for(int j=1; j<n; j++) {
// 只有不是障碍物才能到达该点
if(obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i][j-1] + dp[i-1][j];
}
}
}
return dp[m-1][n-1];
}
}
初始化边界时的错误写法:
// 初始化第一行
for(int i=0; i<n; i++) {
// 等于0,则说明不是障碍物,可以走
if(obstacleGrid[0][i] == 0) {
dp[0][i] = 1;
}
}
// 初始化第一列
for(int i=0; i<n; i++) {
// 等于0,则说明不是障碍物,可以走
if(obstacleGrid[i][0] == 0) {
dp[i][0] = 1;
}
}
64. 最小路径和
分析:
与【剑指 Offer 47. 礼物的最大价值】几乎一模一样,一个是求最大值,一个是求最小值
- 要想 到达某个点的路径是最优的, 那么到达这个点的上一步的路径一定也是最优的,这是一道典型的动态规划问题
- 状态转移方程为:
dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j] - 步骤:遍历二维数组,填表
代码:
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m][n];
// 起点初始化为 grid[0][0]
dp[0][0] = grid[0][0];
// 初始化第一行
for(int i=1; i<n; i++) {
dp[0][i] = dp[0][i-1] + grid[0][i];
}
// 初始化第一列
for(int i=1; i<m; i++) {
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for(int i=1; i<m; i++) {
for(int j=1; j<n; j++) {
dp[i][j] = Math.min(dp[i][j-1], dp[i-1][j]) + grid[i][j];
}
}
return dp[m-1][n-1];
}
}
5. 最长回文子串(中心扩展法,非动态规划解法)
解法一:暴力 - 遍历所有字串
建议先做第9题【9. 回文数】
代码:
class Solution {
public String longestPalindrome(String s) {
String longestPalindrome = "";
// 遍历所有的子串,若长度比longestPalindrome长 且 是回文串,则更新longestPalindrome
for(int i=0; i<s.length(); i++) {
for(int j=i; j<s.length(); j++) {
if(j - i + 1 > longestPalindrome.length()) {
if(isPalindrome(s.substring(i, j+1))) {
longestPalindrome = s.substring(i, j+1);
}
}
}
}
return longestPalindrome;
}
// 判断是否是回文字符串
public Boolean isPalindrome(String s) {
// 双指针
int left = 0;
int right = s.length() - 1;
while (left <= right) {
if(s.charAt(left) != s.charAt(right)) {
return false;
}
left ++;
right --;
}
return true;
}
}
总结注意点:
- 第一步:先写出 判断是否回文 的方法
isPalindrome。 (利用双指针的思想) - 第二步:暴力遍历每个子字符串,判断是否回文,更长的则更新
时间复杂度: n^3
解法二:中心扩展法
参考讲解视频:https://www.bilibili.com/video/BV1dN4y1g7p9/?spm_id_from=333.337.search-card.all.click&vd_source=bf2066b8675548fac384ffe3bc83793e
代码:
class Solution {
// 维护最长回文字符串
public String res;
public String longestPalindrome(String s) {
// 判空处理
if(null == s && s.length() == 0) {
return "";
}
// 初始化res
res = s.substring(0,1);
// 遍历s字符串
for(int i=0; i<s.length(); i++) {
// 考虑 bab 的格式
extendFromCenter(s, i, i);
// 考虑 baab 的格式
extendFromCenter(s, i, i+1);
}
return res;
}
// 中心扩散
public void extendFromCenter(String s, int left, int right) {
// 当 left、right 在区间返回内,且 s[left] == s[right] 才会向外扩散
while(left>=0 && right<s.length() && s.charAt(left)==s.charAt(right)) {
// 向外扩散
left--;
right++;
}
// 若当前回文串 比 res长 则更新res
if(right - left - 1 > res.length()) {
// 因为最后一次循环 left-- right++了,因此实际上回文字符串是[left+1, right-1],由于substring是左闭右开[),因此 res = s.substring(left+1, right)
res = s.substring(left+1, right);
}
}
}
总结注意点:
- 解法一:判断字串是否是回文串,思想是
自外向内的,left ++; right --; - 解法二:寻找属于回文串的字串,且思想是
自内向外扩散的,left--; right++; - 要考虑
bab、baab两种回文串的格式, 因此在遍历到某个字符时,extendFromCenter(s, i, i);extendFromCenter(s, i, i+1);要调两次extendFromCenter
时间复杂度:n^2
1143. 最长公共子序列
分析:
- 根据两个字符串的长度,创建一个二维表格
- 遍历二维表格。也即是遍历 两个字符串的每一个字符,两两比较
具体详解可参考视频:【最长公共子序列 - 动态规划 Longest Common Subsequence - Dynamic Program】
代码:
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
char[] charArr1 = text1.toCharArray();
int len1 = charArr1.length;
char[] charArr2 = text2.toCharArray();
int len2 = charArr2.length;
// dp[i][j]含义:字符串text1[0,1) 与 字符串text2[0,j) 的最长公共子序列长度
int[][] dp = new int[len1+1][len2+1];
for(int i=1; i<=len1; i++) {
for(int j=1; j<=len2; j++) {
// text1的第i个字符
char ch1 = charArr1[i-1];
// text2的第j个字符
char ch2 = charArr2[j-1];
if(ch1 == ch2) {
// 两个字符串各移除一个字符的状态(↖状态) + 1
dp[i][j] = dp[i-1][j-1] + 1;
} else {
// text1移除一个字符的状态(↑状态),text2移除一个字符的状态(↓状态)。二者求最大值
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[len1][len2];
}
}
技巧
169. 多数元素
分析:
某个值在该数组中的个数超过一半,该值即叫做多数元素,这样的元素在这个数组中肯定只有一个
摩尔投票算法 可以使空间复杂度O(1),时间复杂度为O(n).
B站上上视频讲解:https://www.bilibili.com/video/BV1Ey4y1n7hb
代码:
public class Solution {
/* 摩尔投票 */
public int MoreThanHalfNum_Solution(int [] arr) {
// 票数
int rating = 0;
// m假设是个数超过一半的那个数
int m = arr[0];
for(int i=0; i<arr.length; i++) {
// 当票数为0时, 将当前数当做m,并且票数设为1
if(rating == 0){
m = arr[i];
rating = 1;
} else {
if(arr[i] == m) // 若与m相同 票数就++
rating++;
else // 不同则--
rating--;
}
}
return m;
}
}
136. 只出现一次的数字
【136. 只出现一次的数字】
![]()
分析:
这道题主要利用位运算中异或的性质
异或:二进制下用1表示真,0表示假,则异或的运算法则为:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同为0,异为1)
对于这道题,可使用异或运算 ⊕。异或运算有以下三个性质。
- 任何数和 0 做异或运算,结果仍然是原来的数,即
a⊕0=a。 - 任何数和其自身做异或运算,结果是 0,即
a⊕a=0。 - 异或运算满足交换律和结合律,即
a⊕b⊕a =b⊕a⊕a = b⊕(a⊕a) = b⊕0=b。
因为该数组中只有一个数出现一次,其他数都是出现两次,所有若让数组中所有的数参与异或运算,最终的结果肯定是只出现一次的那个数。
代码:
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for(int i=0; i<nums.length; i++) {
res ^= nums[i];
}
return res;
}
}
75. 颜色分类
分析:
经典【荷兰国旗】问题。
我们要对该数组排序,排序的规则就是 0 放到最左边,2 放到最右边, 1 放到中间
需要三个指针,left、right、curIdx
left下标之前的元素都是 0right下标之后的元素都是 2curIdx表示当前要判断的元素下标
步骤:
- 使用curIdx遍历所有元素,当
curIdx > right时遍历终止 - 若
nums[curIdx] == 0,则将当前元素移动到left之前,并且curIdx可后移(因为curIdx之前的元素本身已经有序了,不需要再判断了)。具体操作如下:swap(nums, curIdx, left++)curIdx++
- 若
nums[curIdx] == 2,则将当前元素移动到right之后,但curIdx不可后移(因为curIdx后面的元素还未排序,仍需要判断)。具体操作如下:swap(nums, curIdx, right--)
- 若
nums[curIdx] == 1,本身符合排序规则,则curIdx直接后移即可。具体操作:curIdx++
参考视频:【LeetCode.75.颜色分类】
参考题解:【【宫水三叶】经典荷兰国旗问题】
代码:
class Solution {
public void sortColors(int[] nums) {
int len = nums.length;
int curIdx = 0;
int left = 0;
int right = len - 1;
// 当curIdx > right 时才算遍历完了所有元素
while(curIdx <= right) {
if(nums[curIdx] == 0) {
// 将当前值已到left左侧
swap(nums, curIdx, left++);
// curIdx之前的元素本身是有序的,因此curIdx可直接后移
curIdx++;
} else if (nums[curIdx] == 2) {
// 将当前值已到right右侧
swap(nums, curIdx, right--);
// curIdx之后的元素还未排序,curIdx不可直接后移
} else {
// nums[curIdx] == 1,当前符合顺序,curIdx可直接后移
curIdx++;
}
}
}
// 数值交换
public void swap(int[] nums, int idx1, int idx2) {
int temp = nums[idx1];
nums[idx1] = nums[idx2];
nums[idx2] = temp;
}
}
287. 寻找重复数
分析:
可看成寻找环形链表的入环节点
详细题解可参考大佬解释:【287.寻找重复数】
代码:
class Solution {
public int findDuplicate(int[] nums) {
int slow = 0, fast = 0;
slow = nums[slow]; // 慢指针,一次走一步
fast = nums[nums[fast]]; // 快指针,一次走两步
while(slow != fast) {
// 慢指针,一次走一步
slow = nums[slow];
// 快指针,一次走两步
fast = nums[nums[fast]];
}
// 快指针 或者 慢指针 从头结点出发(指针指向pHead),慢指针从相遇点出发(指针指向不变)
slow = 0;
// 新一轮移动 一个指针从头结点 一个指针从相遇节点(哪个从头结点哪个从相遇点都无所谓)
while(slow != fast) {
// 快慢指针后移 每轮都走一步
slow = nums[slow];
fast = nums[fast];
}
// 当快慢指针再次相遇时 就是入环节点
return fast;
}
}