堆排序解析

                                                                            堆排序
一、简介

备注：简介，代码来源，均来自于菜鸟教程:https://www.runoob.com/w3cnote/heap-sort.html,本文主要是对算法进行讲解，方便自己记忆以及大家理解。

1、堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

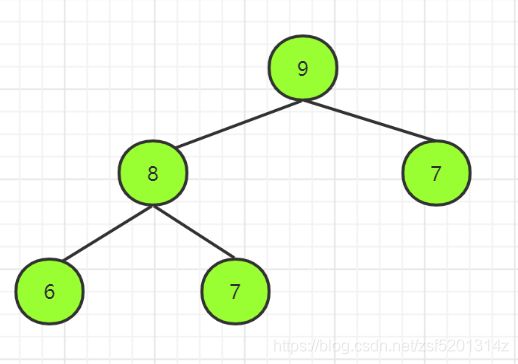
1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
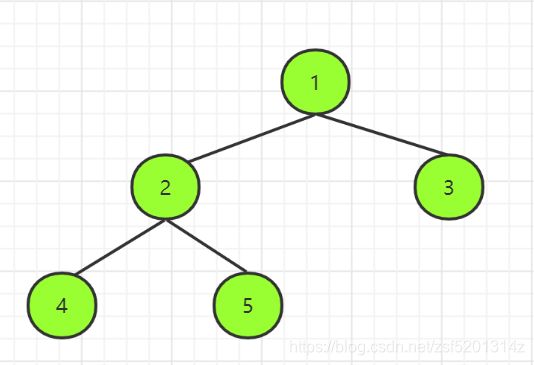
2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；
3. 对应通项公式如下:(i代表在数组中的位置，2i+1表示左节点在数组的下标 ，2i+2为有节点在数组的下标)
4. 大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

5. 小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

2、时间复杂度：堆排序的平均时间复杂度为 Ο(nlogn)。

3、大顶堆，每个节点的值都大于或者等于子节点的值                                                                                        

 

4、 小顶堆，每个节点的值都小于或者等于子节点的值

二、算法思路

（升序排序），堆用数组进行存储，是形式上的树，非真实的树，通过下标来关联父子关系

1、首先对N个节点，构建一个大顶堆

2、构建完大顶堆后，把根节点和最后一个叶子节点互换

3、对N-1个节点再次构建大顶堆，第N个元素已经是最大值了，不需要重新构建大顶堆，

4、之后操作就是重复2,3的操作，直到堆的尺寸为 1

 

三、算法解析（以数组{3,4,5,7,8}为例）

1、构建大顶堆，自下往上构建

    private static void buildMaxHeap(int[] arr, int len) {
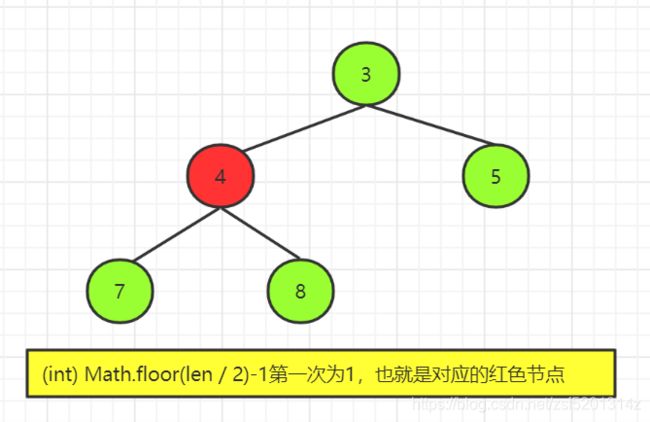
        //向下取整，取完全二叉树最后一个元素的父节点对应在数组的位置
        int lastParentArrayPos = (int) Math.floor(len / 2)-1;
        System.out.println("level : "+lastParentArrayPos);
        //currentBuildMaxHeapPos 当前生成最大堆的的位置
        for (int currentBuildMaxHeapPos = lastParentArrayPos; currentBuildMaxHeapPos >= 0; currentBuildMaxHeapPos--) {
            heapify(arr, currentBuildMaxHeapPos, len);
        }
    }

2、构建大顶堆，调整顺序

首先计算本次构建的节点的左右子节点的位置，也就是节点4的左右子节点，7,8的位置，对应的NodePos=3,4(数组的位置)

        //左子树在数组的位置
        int leftNodePos = 2 * currentBuildMaxHeapPos + 1;
        //右子树在数组的位置
        int rightNodePos = 2 * currentBuildMaxHeapPos + 2;
        //当前构建堆的位置（数组）(两个子节点的父节点位置)
        int currentPos = currentBuildMaxHeapPos;

3、构建大顶堆，判断左边子节点是否大于父节点，如果大于那么标记当前的位置，后面需要交换

        /**
         * leftNodePos < arrayLength 避免父节点无子节点，确保子节点存在
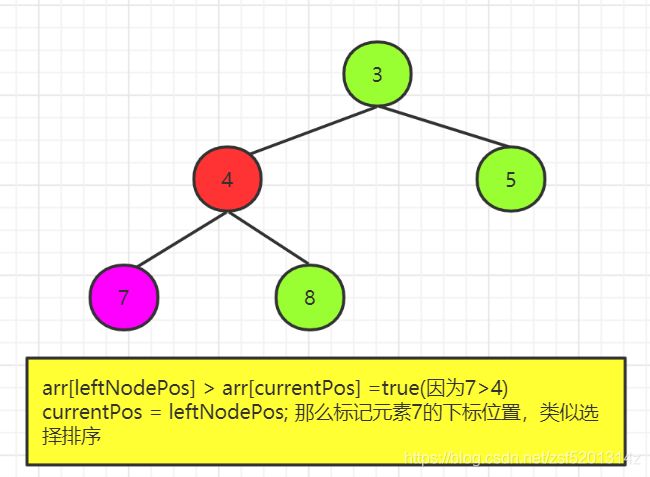
         * arr[leftNodePos] > arr[currentPos]，如果子节点大于父节点，那么标记为替换的节点
          */
        if (leftNodePos < arrayLength && arr[leftNodePos] > arr[currentPos]) {
            currentPos = leftNodePos;
        }

4、构建大顶堆，判断右边子节点是否大于父节点，如果大于那么标记当前的位置，后面需要交换

        /**
         * rightNodePos < arrayLength 避免父节点无子节点，确保子节点存在，
         * arr[rightNodePos] > arr[currentPos]，如果子节点大于父节点，那么标记为替换的节点
         */
        if (rightNodePos < arrayLength && arr[rightNodePos] > arr[currentPos]) {
            currentPos = rightNodePos;
        }

 

5、构建大顶堆，判断当前处理的根节点位置是否有变动，如果有变动，那么交换根节点的位置，并对修改过的值进行重新构建

  /**
         * 判断当前位置跟原来的位置是否相同，如果不同说明需要构建堆的过程中做了位置调整
         */
        if (currentPos != currentBuildMaxHeapPos) {
            //交换位置，类似于选择排序，先标记再交换
            swap(arr, currentBuildMaxHeapPos, currentPos);
            //交换元素后再继续构建大顶堆
            heapify(arr, currentPos, arrayLength);
        }

6、交换根节点与最后一个子节点，并继续构建大顶堆

 for (int i = len - 1; i > 0; i--) {
            //交换根节点跟最后一个叶子结点
            swap(arr, 0, i);
            //堆节点数-1，因为最后一个元素已经排序了
            len--;
            //继续构建大顶堆
            heapify(arr, 0, len);
        }

三、完整代码

package org.example.sort;

import java.util.Arrays;
import java.util.Random;

public class HeapSort {

    public static void main(String[] args ){
        int size = 10000000;
        int[] defaultList = new int[]{3,4,5,7,8};
        int[] sourceArray = generateArray(size, null);
        long l = System.currentTimeMillis();
        int[] sortedArray = sort(sourceArray);
        System.out.println("sort"+size+" items cost : "+(System.currentTimeMillis()- l) + "ms");
       // printArray(sortedArray);
    }

    public static void printArray(int[] array){
        System.out.println("start print array");
        for (int i:array ) {
            System.out.print(i+" ,");
        }
        System.out.println();
        System.out.println("print array end");
    }

    public static int[] generateArray(int size, int[] defaultList){
        if(defaultList != null){
            return defaultList;
        }
        int[] array = new int[size];
        Random r = new Random();
        for (int i=0;i 0; i--) {
            //交换根节点跟最后一个叶子结点
            swap(arr, 0, i);
            //堆节点数-1，因为最后一个元素已经排序了
            len--;
            //继续构建大顶堆
            heapify(arr, 0, len);
        }
        return arr;
    }

    private static void buildMaxHeap(int[] arr, int len) {
        //向下取整，取完全二叉树最后一个元素的父节点对应在数组的位置
        int lastParentArrayPos = (int) Math.floor(len / 2)-1;
        System.out.println("level : "+lastParentArrayPos);
        //currentBuildMaxHeapPos 当前生成最大堆的的位置
        for (int currentBuildMaxHeapPos = lastParentArrayPos; currentBuildMaxHeapPos >= 0; currentBuildMaxHeapPos--) {
            heapify(arr, currentBuildMaxHeapPos, len);
        }
    }

    /**
     *
     * @param arr 待排数组
     * @param currentBuildMaxHeapPos 当前构建大顶堆的位置（数组上的位置）
     * @param arrayLength
     */
    private static void heapify(int[] arr, int currentBuildMaxHeapPos, int arrayLength) {
        //左子树在数组的位置
        int leftNodePos = 2 * currentBuildMaxHeapPos + 1;
        //右子树在数组的位置
        int rightNodePos = 2 * currentBuildMaxHeapPos + 2;
        //当前构建堆的位置（数组）(两个子节点的父节点位置)
        int currentPos = currentBuildMaxHeapPos;

        /**
         * leftNodePos < arrayLength 避免父节点无子节点，确保子节点存在
         * arr[leftNodePos] > arr[currentPos]，如果子节点大于父节点，那么标记为替换的节点
          */
        if (leftNodePos < arrayLength && arr[leftNodePos] > arr[currentPos]) {
            currentPos = leftNodePos;
        }

        /**
         * rightNodePos < arrayLength 避免父节点无子节点，确保子节点存在，
         * arr[rightNodePos] > arr[currentPos]，如果子节点大于父节点，那么标记为替换的节点
         */
        if (rightNodePos < arrayLength && arr[rightNodePos] > arr[currentPos]) {
            currentPos = rightNodePos;
        }

        /**
         * 判断当前位置跟原来的位置是否相同，如果不同说明需要构建堆的过程中做了位置调整
         */
        if (currentPos != currentBuildMaxHeapPos) {
            //交换位置，类似于选择排序，先标记再交换
            swap(arr, currentBuildMaxHeapPos, currentPos);
            //交换元素后再继续构建大顶堆
            heapify(arr, currentPos, arrayLength);
        }
    }

    private static  void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

}