LeetCode 热题 HOT 100 第七十五天 347. 前K个高频元素 中等题 用python3求解
题目地址
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
1 <= nums.length <= 10^5
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的
进阶:你所设计算法的时间复杂度必须优于O(nlogn) ,其中n是数组大小。
解题方案:堆
参考:指路
这题是对 堆,优先队列 很好的练习,因此有必要自己用python实现研究一下。堆 处理海量数据的 topK,分位数 非常合适,优先队列 应用在元素优先级排序,比如本题的频率排序非常合适。与基于比较的排序算法 时间复杂度 O(nlogn)O(nlogn) 相比,使用 堆,优先队列 复杂度可以下降到 O(nlogk)O(nlogk),在总体数据规模 n 较大,而维护规模 k 较小时,时间复杂度优化明显。
解题思路:
堆:处理海量数据的 topK、分位数非常合适,比如本题求topK。
优先队列:应用在元素优先级排序非常合适,比如本题求topK且按频率输出排序。
与基于比较的排序算法 时间复杂度O(nlogn)相比,使用堆,优先队列的复杂度可以下降到O(nlogk),在总体数据规模n较大,而维护规模k较小时,时间复杂度优化明显。
堆,优先队列的本质其实就是个完全二叉树,有其下重要性质
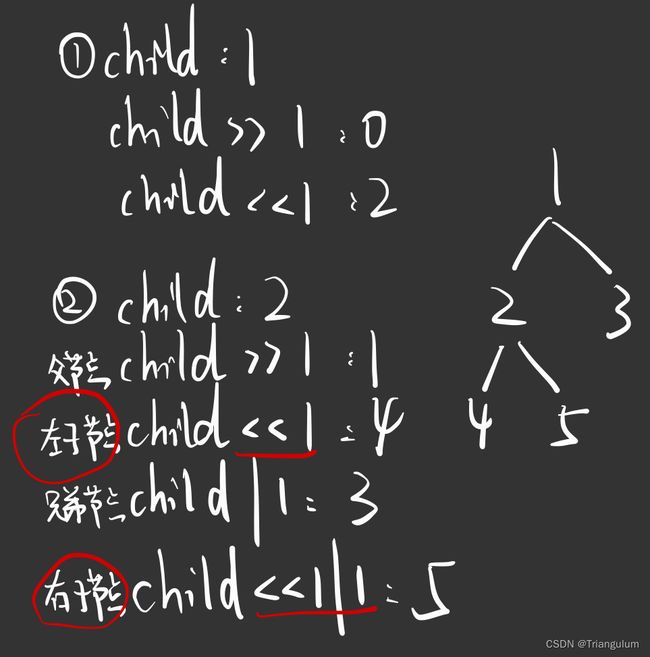
注: 堆heap[0]插入一个占位节点,此时堆顶为index为1的位置,可以更方便的运用位操作:[1,2,3] -> [0,1,2,3]
1.父节点 index 为 i
2.左子节点 index 为 i << 1
3.右子节点 index 为 i << 1 | 1
4.大顶堆中每个父节点大于子节点,小顶堆每个父节点小于子节点
5.优先队列以优先级为堆的排序依据
因为性质 1,2,3,堆可以用数组直接来表示,不需要通过链表建树。
堆,优先队列有两个重要操作,时间复杂度均是O(logk)。以小顶锥为例:
1.上浮sift up: 向堆尾新加入一个元素,堆规模 +1,依次向上与父节点比较,如小于父节点就交换。
2.下沉sift down: 从堆顶取出一个元素(堆规模 -1,用于堆排序)或者更新堆中一个元素(本题),依次向下与子节点比较,如大于子节点就交换。
对于topk问题:最大堆求topk小,最小堆求topk大。
topk小:构建一个 k 个数的最大堆,当读取的数小于根节点时,替换根节点,重新塑造最大堆
topk大:构建一个 k 个数的最小堆,当读取的数大于根节点时,替换根节点,重新塑造最小堆
这一题的总体思路
总体时间复杂度O(nlogk)
遍历统计元素出现频率O(n)
前k个数构造规模为k+1的最小堆minheap,O(k),注意+1是因为占位节点。
遍历规模k之外的数据,大于堆顶则入堆,下沉维护规模为k的最小堆minheap,O(nlogk)。
(如需按频率输出,对规模为k的堆进行排序)
代码实现:
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
def sift_down(arr, root, k):
"""下沉log(k),如果新的根节点>子节点就一直下沉"""
val = arr[root] # 用类似插入排序的赋值交换,arr[root]为堆顶元素
#root为1,则root<<1为2
while root<<1 < k:
child = root << 1
#指定child的位置,此时child为root的左子节点,child|1为child的兄弟节点,也就是child|1为root的右子节点
#选取左右孩子中小的与父节点交换(如果右子节点<左子节点,把child的位置指定为右子节点的位置)
if child|1 < k and arr[child|1][1] < arr[child][1]:
child |= 1 #child = child|1
# 如果子节点<新节点,交换,如果已经有序break
if arr[child][1] < val[1]:
arr[root] = arr[child]
root = child
else:
break
arr[root] = val
def sift_up(arr, child):
"""上浮log(k),如果新加入的节点<父节点就一直上浮"""
#child为某节点索引,那么child>>1为其父节点索引,child<<1为其左子节点,
val = arr[child]
while child>>1 > 0 and val[1] < arr[child>>1][1]:
arr[child] = arr[child>>1]
child >>= 1
arr[child] = val
stat = collections.Counter(nums) #stat: Counter({1: 3, 2: 2, 3: 1})
stat = list(stat.items()) #stat: [(1, 3), (2, 2), (3, 1)]
heap = [(0,0)]
# 构建规模为k+1的堆,新元素加入堆尾,上浮
for i in range(k):
#由0->3->2变为0->2->3
heap.append(stat[i]) #i为0,heap:[(0, 0), (1, 3)];i为1,heap:[(0, 0), (1, 3), (2, 2)]
sift_up(heap, len(heap)-1)#i为0,heap:[(0, 0), (1, 3)];i为1,heap:[(0, 0), (2, 2), (1, 3)]
# 维护规模为k+1的堆,如果新元素大于堆顶,入堆(替换堆顶),并下沉
for i in range(k, len(stat)):
if stat[i][1] > heap[1][1]:
heap[1] = stat[i]
sift_down(heap, 1, k+1)
return [item[0] for item in heap[1:]]