动手学深度学习之生成对抗网络

参考伯禹学习平台《动手学深度学习》课程内容内容撰写的学习笔记
原文链接：https://www.boyuai.com/elites/course/cZu18YmweLv10OeV/lesson/yxuHJjjhqYCh3thUzcVXaN
感谢伯禹平台，Datawhale，和鲸，AWS给我们提供的免费学习机会！！
总的学习感受：伯禹的课程做的很好，课程非常系统，每个较高级别的课程都会有需要掌握的前续基础知识的介绍，因此很适合本人这种基础较差的同学学习，建议基础较差的同学可以关注伯禹的其他课程：
数学基础：https://www.boyuai.com/elites/course/D91JM0bv72Zop1D3
机器学习基础：https://www.boyuai.com/elites/course/5ICEBwpbHVwwnK3C
本篇总结部分来源于：深度学习算法与计算机视觉公众号，需要的可以进行关注。代码部分，来自伯禹平台。

引言

GAN已经作为一种思想来渗透在ML的其余领域，做出了很多很Amazing的东西。被Yann LeCun评价为近十年最有趣的idea，所以对于相关研究方向的同学而言，gan成了一个必须要学的思想和方法。

基本概念

GAN中包括两个最基本的组件，其中一个就是Generator，对于Image Generation过程来说，你给它一个向量，它输出一个图片(image)。

input: vector

output: image

如下所示：

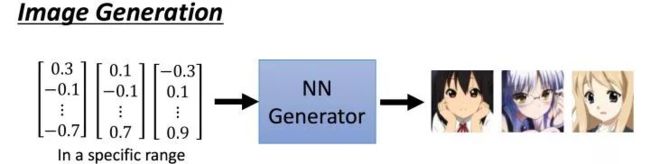
对于Sentence Generation来说，你给它一个向量，它输出一个句子(sentence)。

input: vector

output: sentence

如下所示：

其中我们以image generation过程来仔细说明一下其中过程原理！

实际上Generator就是一个NN网络，输入是一个vector，它的输出是一个高维的向量，比如image是16*16，那么它的输出就是256维的向量。

如图所示：

其中，输入向量的每一个维度都可以代表输出image的某些特征，比如说第一维度的值，代表着image人物的头发长短。

那么我们在调大input vector的第一维的值的时候，我们可以看到生成的image的头发变长，如下图所示：

或者说，input vector某一个维度的值大小代表生成image的口张开的大小，调大后，生成的image人物中口张的更大一些：

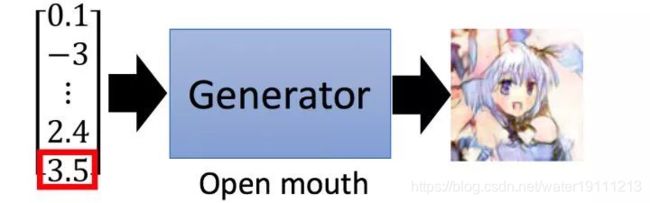
总而言之，GAN中的Generator就是一个神经网络，丢给它一个输入向量，输出也是一个向量。

在不同的任务中，生成的东西不同，输入向量的每一个维度都代表着输出image的特定特征。

生成器基本概念

讲完了Generator之后，我们来看GAN的另一个组件，Discriminator。Discriminator也是一个NN网络，它的输入是Generator的输出或者是真实的image…，输出是一个标量，代表接受的输入的quality有多好，数值越大，代表越好，数值越小，代表越差。

如下图：

比如给它输入是真实的image，那么经过Discriminator之后应该是输出的标量值很大，代表送入给它的image的质量很高。

比如给它输入是差的image，那么经过Discriminator之后应该是输出的标量值很小，代表送入给它的image的质量很低。

GAN算法

下面我们来介绍一下最基本的gan的训练算法，不够严谨，但是容易接受。

首先，跟任何网络训练一样，我们需要初始化生成器G，和判别器D的参数

形式化公式就是如下：

1、然后在每一轮中，首先固定住G，训练D，具体怎么训练呢？

我们任意选取一些向量，送给G，同时从database中挑选出一些数据，使得判别器学会从database挑选出真实的图片打分高，任意选取向量从G中生成的图片，打分低。这样就是在训练判别器：

形式化公式如下：

稍微解释一下图片中的公式，训练判别器就是希望它对于真实的图片打分高，生成的图片打分低。而公式中是最大化那个式子，分解来看完全对应文字的解释：
对应真正的图片打分高，也就是最大化如下公式，公式如下：

2、第二步是固定判别器D，训练生成器G，我们还是任意给定一些向量，这些向量送给G，生成一些图片，然后喂进判别器进行判别。

首先我们的目的是使得生成器能够生成非常真实的图片，对于真正真实的图片来说，判别器的打分是高的，那么也就是说，我们需要训练生成器，使得通过生成器生成出来的图片让判别器打分高，尽可能的迷惑判别器，这样通过生成器生成出来的图片就是接近“真实的”，土话说就是跟真的好像啊。

形式化公式如下：

公式解释为：最大化使得判别器对于生成器生成的图片打分。

这里需要注意的是训练生成器的时候，一定要固定判别器的参数，因为在实际实现中，生成器和判别器会构成一个大网络，如果不固定判别器的参数去训练生成器的话。

因为目标是使得最后的得分高，网络这个时候仅仅更新最后一层的参数就能让最后的输出标量非常大，很显然这不是我们希望的，如果固定了判别器后面几个layer，训练前面生成器的参数就能正常学习。

以上内容来源于 深度学习算法与计算机视觉，下面将从代码部分进行讲解：

Generative Adversarial Networks

Throughout most of this book, we have talked about how to make predictions. In some form or another, we used deep neural networks learned mappings from data points to labels. This kind of learning is called discriminative learning, as in, we’d like to be able to discriminate between photos cats and photos of dogs. Classifiers and regressors are both examples of discriminative learning. And neural networks trained by backpropagation have upended everything we thought we knew about discriminative learning on large complicated datasets. Classification accuracies on high-res images has gone from useless to human-level (with some caveats) in just 5-6 years. We will spare you another spiel about all the other discriminative tasks where deep neural networks do astoundingly well.

But there is more to machine learning than just solving discriminative tasks. For example, given a large dataset, without any labels, we might want to learn a model that concisely captures the characteristics of this data. Given such a model, we could sample synthetic data points that resemble the distribution of the training data. For example, given a large corpus of photographs of faces, we might want to be able to generate a new photorealistic image that looks like it might plausibly have come from the same dataset. This kind of learning is called generative modeling.

Until recently, we had no method that could synthesize novel photorealistic images. But the success of deep neural networks for discriminative learning opened up new possibilities. One big trend over the last three years has been the application of discriminative deep nets to overcome challenges in problems that we do not generally think of as supervised learning problems. The recurrent neural network language models are one example of using a discriminative network (trained to predict the next character) that once trained can act as a generative model.

In 2014, a breakthrough paper introduced Generative adversarial networks (GANs) Goodfellow.Pouget-Abadie.Mirza.ea.2014, a clever new way to leverage the power of discriminative models to get good generative models. At their heart, GANs rely on the idea that a data generator is good if we cannot tell fake data apart from real data. In statistics, this is called a two-sample test - a test to answer the question whether datasets $X=\{x_1,\dots ,x_n\}$ and $X^{\prime }=\{x_1^{\prime },\dots ,x_n^{\prime }\}$ were drawn from the same distribution. The main difference between most statistics papers and GANs is that the latter use this idea in a constructive way. In other words, rather than just training a model to say “hey, these two datasets do not look like they came from the same distribution”, they use the two-sample test to provide training signals to a generative model. This allows us to improve the data generator until it generates something that resembles the real data. At the very least, it needs to fool the classifier. Even if our classifier is a state of the art deep neural network.

The GAN architecture is illustrated.As you can see, there are two pieces in GAN architecture - first off, we need a device (say, a deep network but it really could be anything, such as a game rendering engine) that might potentially be able to generate data that looks just like the real thing. If we are dealing with images, this needs to generate images. If we are dealing with speech, it needs to generate audio sequences, and so on. We call this the generator network. The second component is the discriminator network. It attempts to distinguish fake and real data from each other. Both networks are in competition with each other. The generator network attempts to fool the discriminator network. At that point, the discriminator network adapts to the new fake data. This information, in turn is used to improve the generator network, and so on.

The discriminator is a binary classifier to distinguish if the input $x$ is real (from real data) or fake (from the generator). Typically, the discriminator outputs a scalar prediction $o\in \mathbb{R}$ for input $\mathbf{x}$, such as using a dense layer with hidden size 1, and then applies sigmoid function to obtain the predicted probability $D(\mathbf{x})=1/(1+e^{-o})$. Assume the label $y$ for the true data is $1$ and $0$ for the fake data. We train the discriminator to minimize the cross-entropy loss, i.e.,

$$\underset{D}{\min }\{-y\log D(\mathbf{x})-(1-y)\log (1-D(\mathbf{x}))\},$$

For the generator, it first draws some parameter $\mathbf{z}\in {\mathbb{R}}^d$ from a source of randomness, e.g., a normal distribution $\mathbf{z}\sim \mathcal{N}(0,1)$. We often call $\mathbf{z}$ as the latent variable. It then applies a function to generate ${\mathbf{x}}^{\prime }=G(\mathbf{z})$. The goal of the generator is to fool the discriminator to classify ${\mathbf{x}}^{\prime }=G(\mathbf{z})$ as true data, i.e., we want $D(G(\mathbf{z}))\approx 1$. In other words, for a given discriminator $D$, we update the parameters of the generator $G$ to maximize the cross-entropy loss when $y=0$, i.e.,

$$\underset{G}{\max }\{-(1-y)\log (1-D(G(\mathbf{z})))\}=\underset{G}{\max }\{-\log (1-D(G(\mathbf{z})))\}.$$

If the discriminator does a perfect job, then $D({\mathbf{x}}^{\prime })\approx 0$ so the above loss near 0, which results the gradients are too small to make a good progress for the generator. So commonly we minimize the following loss:

$$\underset{G}{\min }\{-y\log (D(G(\mathbf{z})))\}=\underset{G}{\min }\{-\log (D(G(\mathbf{z})))\},$$

which is just feed ${\mathbf{x}}^{\prime }=G(\mathbf{z})$ into the discriminator but giving label $y=1$.

To sum up, $D$ and $G$ are playing a “minimax” game with the comprehensive objective function:

$$mi{n}_{D}ma{x}_G\{-E_{x\sim \text{Data}}logD(\mathbf{x})-E_{z\sim \text{Noise}}log(1-D(G(\mathbf{z})))\}.$$

Many of the GANs applications are in the context of images. As a demonstration purpose, we are going to content ourselves with fitting a much simpler distribution first. We will illustrate what happens if we use GANs to build the world’s most inefficient estimator of parameters for a Gaussian. Let’s get started.

%matplotlib inline
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader
from torch import nn
import numpy as np
from torch.autograd import Variable
import torch

Generate some “real” data

Since this is going to be the world’s lamest example, we simply generate data drawn from a Gaussian.

X=np.random.normal(size=(1000,2))
A=np.array([[1,2],[-0.1,0.5]])
b=np.array([1,2])
data=X.dot(A)+b

Let’s see what we got. This should be a Gaussian shifted in some rather arbitrary way with mean $b$ and covariance matrix $A^{T}A$.

plt.figure(figsize=(3.5,2.5))
plt.scatter(X[:100,0],X[:100,1],color=‘red’)
plt.show()
plt.figure(figsize=(3.5,2.5))
plt.scatter(data[:100,0],data[:100,1],color=‘blue’)
plt.show()
print(“The covariance matrix is\n%s” % np.dot(A.T, A))

batch_size=8
data_iter=DataLoader(data,batch_size=batch_size)

Generator

Our generator network will be the simplest network possible - a single layer linear model. This is since we will be driving that linear network with a Gaussian data generator. Hence, it literally only needs to learn the parameters to fake things perfectly.
class net_G(nn.Module):
def init(self):
super(net_G,self).init()
self.model=nn.Sequential(
nn.Linear(2,2),
)
self.initialize_weights()
def forward(self,x):
x=self.model(x)
return x
def initialize_weights(self):
for m in self.modules():
if isinstance(m,nn.Linear):
m.weight.data.normal(0,0.02)
m.bias.data.zero()

Discriminator

For the discriminator we will be a bit more discriminating: we will use an MLP with 3 layers to make things a bit more interesting.

class net_D(nn.Module):
def init(self):
super(net_D,self).init()
self.model=nn.Sequential(
nn.Linear(2,5),
nn.Tanh(),
nn.Linear(5,3),
nn.Tanh(),
nn.Linear(3,1),
nn.Sigmoid()
)
self.initialize_weights()
def forward(self,x):
x=self.model(x)
return x
def initialize_weights(self):
for m in self.modules():
if isinstance(m,nn.Linear):
m.weight.data.normal(0,0.02)
m.bias.data.zero()

Training

First we define a function to update the discriminator.

Saved in the d2l package for later use

def update_D(X,Z,net_D,net_G,loss,trainer_D):
batch_size=X.shape[0]
Tensor=torch.FloatTensor
ones=Variable(Tensor(np.ones(batch_size))).view(batch_size,1)
zeros = Variable(Tensor(np.zeros(batch_size))).view(batch_size,1)
real_Y=net_D(X.float())
fake_X=net_G(Z)
fake_Y=net_D(fake_X)
loss_D=(loss(real_Y,ones)+loss(fake_Y,zeros))/2
loss_D.backward()
trainer_D.step()
return float(loss_D.sum())

The generator is updated similarly. Here we reuse the cross-entropy loss but change the label of the fake data from $0$ to $1$.

Saved in the d2l package for later use

def update_G(Z,net_D,net_G,loss,trainer_G):
batch_size=Z.shape[0]
Tensor=torch.FloatTensor
ones=Variable(Tensor(np.ones((batch_size,)))).view(batch_size,1)
fake_X=net_G(Z)
fake_Y=net_D(fake_X)
loss_G=loss(fake_Y,ones)
loss_G.backward()
trainer_G.step()
return float(loss_G.sum())

Both the discriminator and the generator performs a binary logistic regression with the cross-entropy loss. We use Adam to smooth the training process. In each iteration, we first update the discriminator and then the generator. We visualize both losses and generated examples.

def train(net_D,net_G,data_iter,num_epochs,lr_D,lr_G,latent_dim,data):
loss=nn.BCELoss()
Tensor=torch.FloatTensor
trainer_D=torch.optim.Adam(net_D.parameters(),lr=lr_D)
trainer_G=torch.optim.Adam(net_G.parameters(),lr=lr_G)
plt.figure(figsize=(7,4))
d_loss_point=[]
g_loss_point=[]
d_loss=0
g_loss=0
for epoch in range(1,num_epochs+1):
d_loss_sum=0
g_loss_sum=0
batch=0
for X in data_iter:
batch+=1
X=Variable(X)
batch_size=X.shape[0]
Z=Variable(Tensor(np.random.normal(0,1,(batch_size,latent_dim))))
trainer_D.zero_grad()
d_loss = update_D(X, Z, net_D, net_G, loss, trainer_D)
d_loss_sum+=d_loss
trainer_G.zero_grad()
g_loss = update_G(Z, net_D, net_G, loss, trainer_G)
g_loss_sum+=g_loss
d_loss_point.append(d_loss_sum/batch)
g_loss_point.append(g_loss_sum/batch)
plt.ylabel(‘Loss’, fontdict={‘size’: 14})
plt.xlabel(‘epoch’, fontdict={‘size’: 14})
plt.xticks(range(0,num_epochs+1,3))
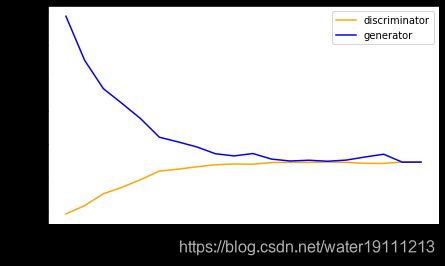
plt.plot(range(1,num_epochs+1),d_loss_point,color=‘orange’,label=‘discriminator’)
plt.plot(range(1,num_epochs+1),g_loss_point,color=‘blue’,label=‘generator’)
plt.legend()
plt.show()
print(d_loss,g_loss)

Z =Variable(Tensor( np.random.normal(0, 1, size=(100, latent_dim))))
fake_X=net_G(Z).detach().numpy()
plt.figure(figsize=(3.5,2.5))
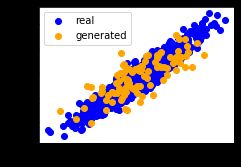
plt.scatter(data[:,0],data[:,1],color='blue',label='real')
plt.scatter(fake_X[:,0],fake_X[:,1],color='orange',label='generated')
plt.legend()
plt.show()

Now we specify the hyper-parameters to fit the Gaussian distribution.
if name == ‘main’:
lr_D,lr_G,latent_dim,num_epochs=0.05,0.005,2,20
generator=net_G()
discriminator=net_D()
train(discriminator,generator,data_iter,num_epochs,lr_D,lr_G,latent_dim,data)

Summary

• Generative adversarial networks (GANs) composes of two deep networks, the generator and the discriminator.
• The generator generates the image as much closer to the true image as possible to fool the discriminator, via maximizing the cross-entropy loss, i.e., $\max \log (D({\mathbf{x}}^{\prime }))$.
• The discriminator tries to distinguish the generated images from the true images, via minimizing the cross-entropy loss, i.e., $\min -y\log D(\mathbf{x})-(1-y)\log (1-D(\mathbf{x}))$.

Exercises

• Does an equilibrium exist where the generator wins, i.e. the discriminator ends up unable to distinguish the two distributions on finite samples?